 Journal of Power and Energy Engineering, 2014, 2, 403-410 Published Online April 2014 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2014.24054 How to cite this paper: Jin, X., et al. (2014) Simulation Analysis of Control System in an Innovative Magnetically-Saturated Controllable Reactor. Journal of Power and Energy Engineering, 2, 403-410. http://dx.doi.org/10.4236/jpee.2014.24054 Simulation Analysis of Control System in an Innovative Magnetically-Saturated Controllable Reactor Xiao Jin1,2, Guoqiang Zhang1, Runrui Guo1 1Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing, China 2School of Computer and Control Engineering, University of Chinese Academy of Sciences, Beijing, China Email: jinxiao@mail.iee.ac.cn Received January 2014 Abstract Controllable saturation reactors are widely used in reactive power compensation. The control system of controllable satu ration reactor determines adaption speed, accuracy, and stability. First, an innovative type of controllable sa tur ation reactor is introduced. After that the control system is designed, and a self-tuning algorithm in PID controller is proposed in the paper. The alg or ith m tunes PID parameters automatically with different error signals caused by varied loads in power system. Then the feasibility of the above algorithm is verified by Simulink module of Matlab soft- ware. The results of simulation indic ate that the control system can efficiently reduce adaption time and overshoot. Keywords Controllable Saturation Reactor; Parameter Self-Tuni ng; PID Controller; Reactive Power Compens ati on 1. Introduction Reactive compensation apparatus are used in power system to reduce losses in power transmis sion line, to en- sure stability of voltage, and to adjust power factor [1]. The Magnetic valve type magn eticall y-saturated con- trollable reactor (MCR) is a main type of reactive compensation apparatus [2]. However, the saturation position of Magnetic valve type MCR is in the main limbs of the iron core, which causes unsatisfa cto ry heat dissipation performance. And Magnetic valve type MCR is three-phase six -li mb structure, which costs a number of mate- rials [3]. An innovative controllable reactor, si de -limes and side-yokes magnetic-saturation type controllable reactor (SSMCR), was proposed by researchers at Chinese Academy of Sciences, Institute of Electrical Engi- neering. The saturation position of SSMCR is changed to side limbs and side yokes, which efficiently improves heat dissipation performance a nd reduces material cost [4]. Control system of MCR plays the key role. PID controller and DC-DC converter are applied in SSMCR to control its reactance. DC-DC convertor uses only one IGBT. PID controllers are extensively used in industrial 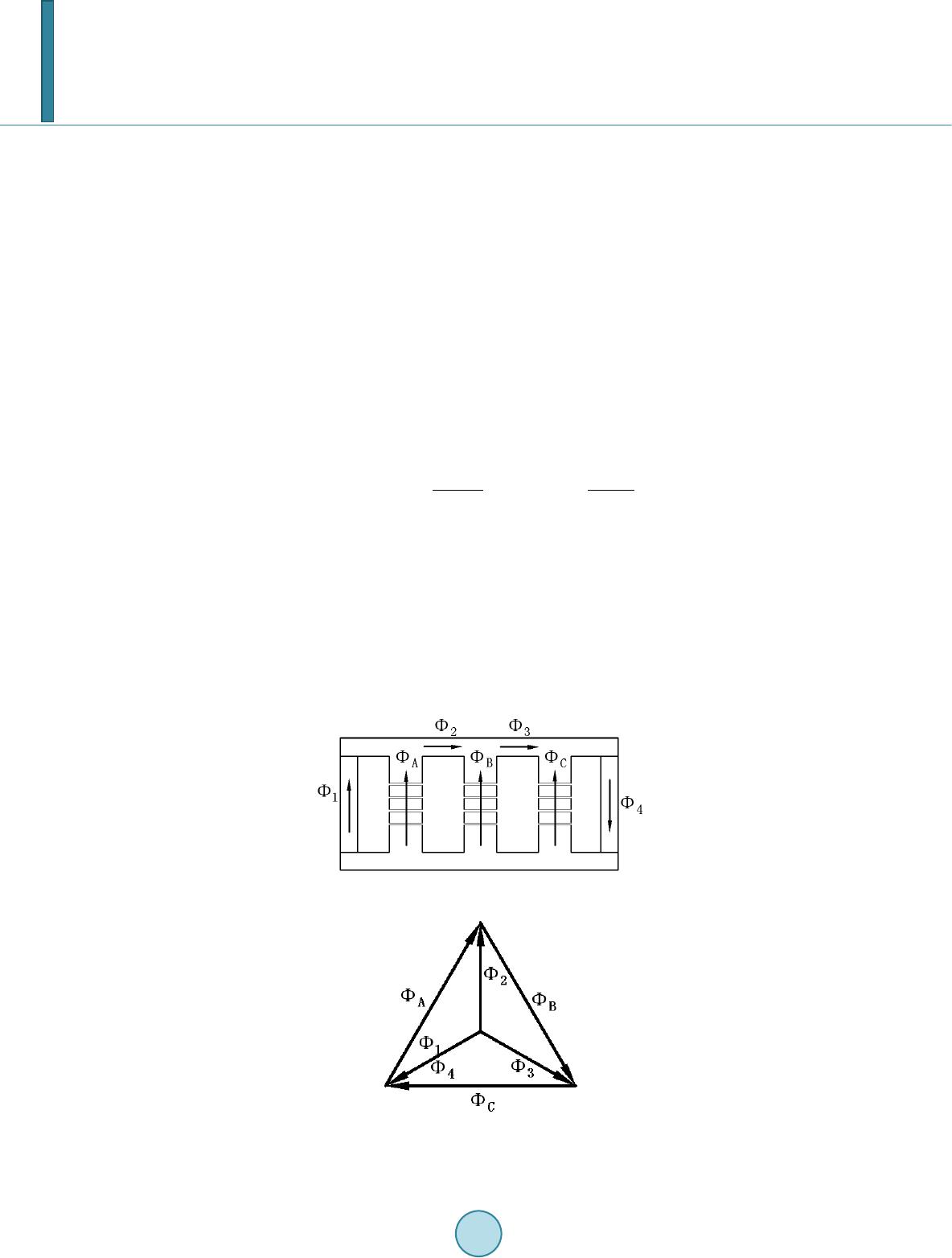 X. Jin et al. automation. However, when applied in nonlinear, high order and time-delayed linear systems, conventional PID controller may cause long adjusting time, big overshoot, and even system out of control [5]. And what’s more, extremely complicated and fuzzy systems have no precise mathematical models. To solve the problems, various modified conventional PID controllers such as expert control were developed [6], and Non-conventional PID controllers based on fuzzy logic and genetic algorithm have been designed as well [7]-[9]. Due to frequent dras- tic variation of loads and nonlinearity of SSMCR, a self-tuning PID control algorithm is proposed in this paper. Then the simulations are conducted to demonstrate its feasibility and effectiveness. 2. Control System Design Figure 1 illustrates the outline of SSMCR. Compared with the magnetism valve type MCR, SSMCR changes its saturation position to side-limes and side yokes. DC exciting windings are installed at side-limes. When ΦA, ΦB and ΦC are sine AC magnetic flux, the Φ1, Φ2, Φ3 and Φ4 are not standard sine wave and contain odd harmonics. Figure 2 is the vector diagram, where Φ1, Φ2, Φ3 and Φ4 are fundamental waves. If the side-limb windings are excited by DC current, the DC flux will flow through side limbs and yokes. Therefore, magnetic saturation level of side limbs and yokes are changed and its magnetic resistances are changed as well. As a result, the reactance of SSMCR is changed. Its reactance can be calculated as follow: 220 2π2πr MF cr fW XfW S RRa l δ µ µµ = = ++ (1) where W is number of turns of AC winding, Rδ is magnetic resistance of air gap, Rc is magnetic resistance of side limbs and yokes, SF is cross-section area of side limbs and yokes. α is a constant related with length of air gap, cro ss-sectio n area of core. μr is relative permeability which reflects the saturation level of material. In conclusion, the reactance of SSMCR can be controlled by the DC current in side-limbs winding. μr is changed with IDC, the equation of μr = f(IDC) cannot be given because of its particular complexity and nonlinear- ity. The relationship IDC − XM of SSMCR shows in Figure 3. The result is obtained by experiments under U = 380 V. Figure 4 shows a typical power grid situation applied SSMCR and Figure 5 is the scheme diagram of control system. ATT7022 is used for as data acquisition equipment (DAE) to collect data of power grid system such as Figure 1. Construction and magnetic circuit of SSMCR. Figure 2. Vector diagram of mag- netic flux. 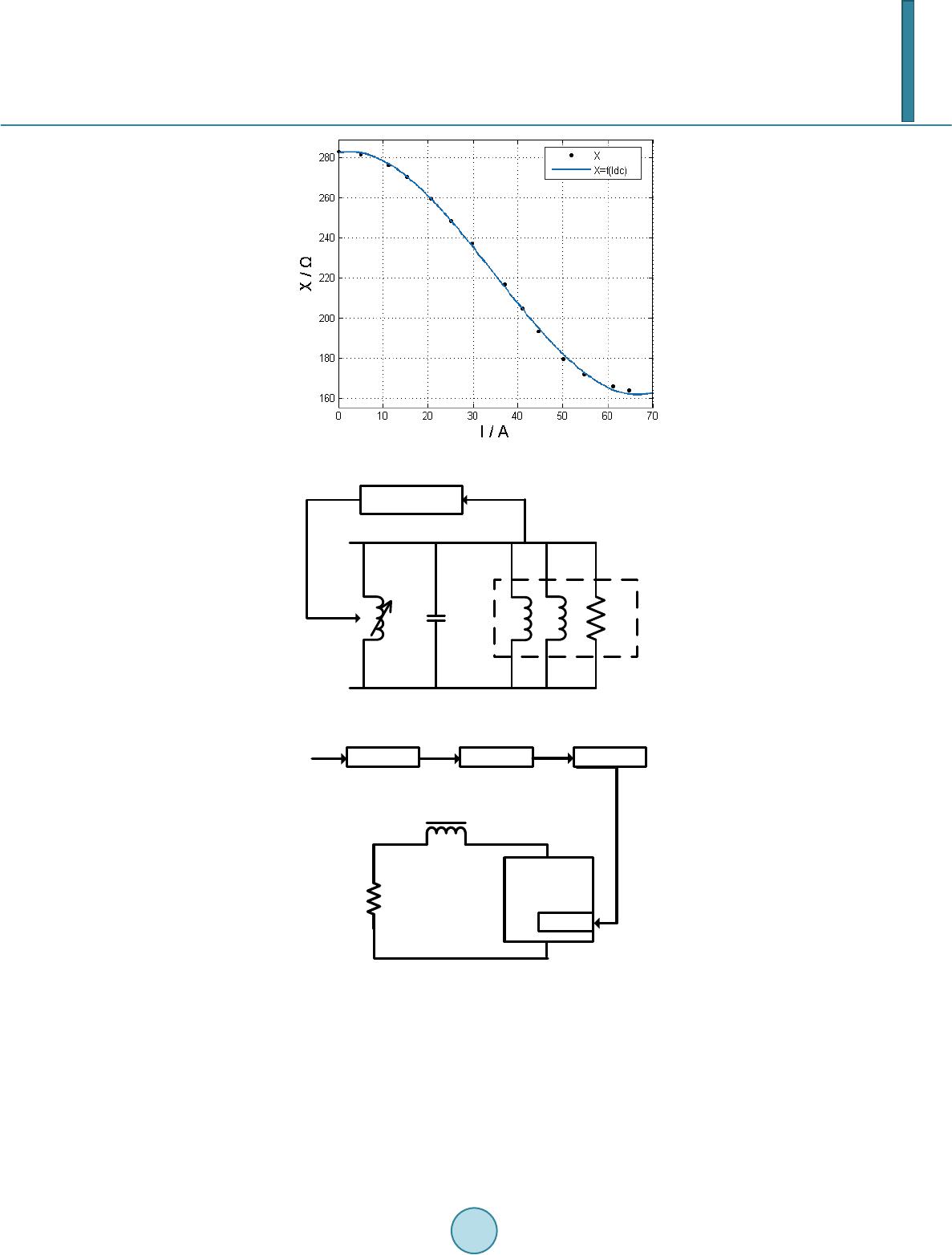 X. Jin et al. Figure 3. Relationship between DC current and reactance. C SSMCR Control System R L1 L2 Load Figure 4. Typical power grid situation applied SSMCR. DC/DC Convertor IGBT ATT7022 STM32 AT89S52 Side-limb winding Power Grid Signal Phase angle Figure 5. Scheme diagram of control system. power factor and phrase angle. STM32 is used as the PID controller which controls the phrase angle (or power factor) of SSMCR to a certain set-point. And the AT89S52 is used as exec uto r to drive the IGBT. In our system, the control system adapts the reactance of SSMCR in terms of phrase angle. 3. Self-Tuning PID Control Algorithm PID controller controls the system based on error signal between set-point and system output. Figure 6 illu- strates the PID controller of SSMCR. 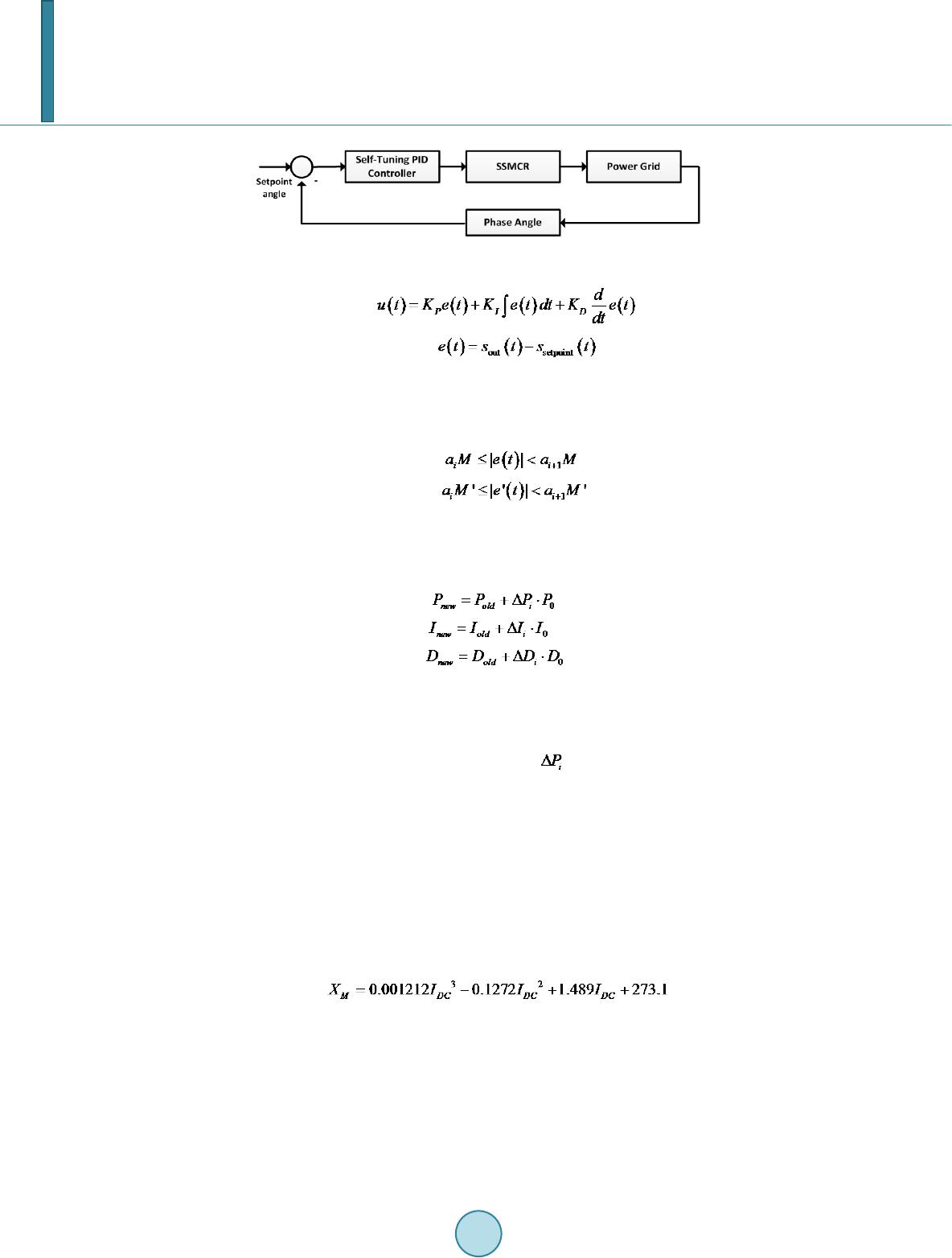 X. Jin et al. Figure 6. Schematic d iagr am of PID controller. (2) (3) where KP, KI and KD are proportional, inte gra l and derivative parameters. KP depends on the prese nt error, KI depends on the accumulation of past errors, and KD is a prediction of future errors, based on current change rate [5]. A cla ssificatio n method of error signal |e(t)| (or |e’(t)| when it comes to d er i vative) is given as Ri: (4) (5) where 0 ≤ ai < ai+1 ≤ 1, 0 < i ≤ N, N ∈ Z*. M and M’ is the max i mu m of expected error. Based on classification of error signals, parameters tuning principle is designed as: when error signal |e(t)| (or |e’(t)|) rises, proportional should rise, integral should decrease, and derivative should rise. Parameter adaption rules are given (Ri): (6) (7) (8) where Pnew, Inew and Dne w are the results of parameter tuning. Pold, Iold and Dold are values before parameter tuning. P0 is the original value of PID controller. ΔP is adaption rate and |ΔP| < 1. ΔP is regarded as the adaption speed of proportional. When SSMCR is working, the parameters are changed frequently by the controller based on the proposed al- gorithm. In terms of different classification of error signals, can be found in the rule-table which is given based on SSMCR. Therefore, parameters can be changed in different speeds. Part of rule-table is given in the Table 1. 4. Simulations The feasibility and effectiveness of the proposed algorithm are simulated on Matlab. Input is random step signal and outputs are produced by conventional PID controller and self-tuning PID controller. According to output curves (Figure 7), the overshoot produced by conventional PID controller is 7.3% of input variatio n in average and adaption time is 0.91 s in average. Compared with conventional PID algorithm, the self-tuning PID algo- rithm can efficiently reduce adaption time to 0.13 s and overshoot to zero. The model of SSMCR is built as follow. The result is produced by curve fitting based on data in Figure 3. (9) where XM is reactance of SSMCR and IDC is exciting DC current. In order to simulate the self-tuning PID algorithm in typical power grid situation in terms of Figure 4, the re- sistanc e (R) a nd inductanc e (L) of load, and capacitance (C) of compe nsation capacitor should be chosen prop- erly for building the simulation model. When C and L are fixed and R varies, the Figure 8 shows the controlla- ble zone of SSMCR. And Figure 9 is on the situation that R and L are fixed and C varies. Controllable zone is the area between the two curves (maximum curve and minimum curve of system phrase angle). According to Figures 8 and 9, we chose R = 1000 Ω and C = 20 μF. On this situation, the controllable zone shows in Figure 10. 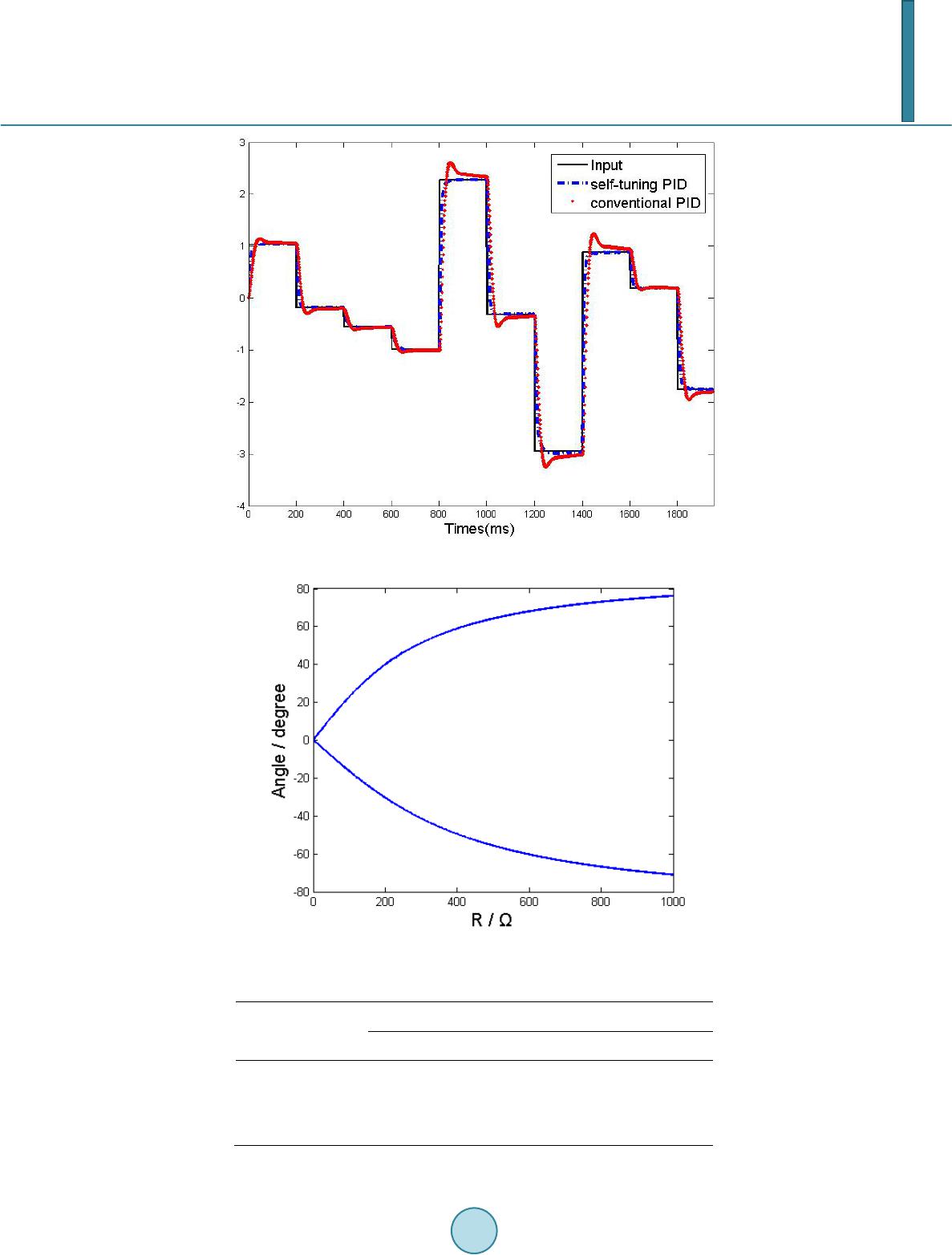 X. Jin et al. Figure 7. Outputs of conventional and self-tuning algorithm. Figure 8. Controllable zone with resistance of loads. Table 1. Part of rule-table of proportional. Interval P roport ion al Δ Min Max [0, 0.25) 0.480 1.00 3.00 [0.25, 0.5) 0.270 1.00 3.00 [0.5, 0.65) 0.150 1.00 3.00  X. Jin et al. Figure 9. Controllable zone with capacitan ce of capacitor. Figure 10. Controllable zone with inductance of loads. According to Figure 10, when 150 Ω < XL < 800 Ω, the phrase angle of system can be controlled from −43.2˚ to 32.0˚. Therefore, we chosen L = 2.86 H. The system model is built in Simulink as shown in Figure 11. In system simulation, input voltage is 380 V and set -point is set to 18.2 (namely cosφ = 0.95). L1 and L2 are switched off and switched on in turns to change the structure of load. According to Figures 8-10, the controller could control the phase angle of system to set- point. Figure 12 shows the control result of PID controller and Figure 13 shows the IDC cu r ve. SSMCR with sel f-tuning PID algorithm can reduce the adaption time to 0.08 s. The overshoots of both phase angle and DC exciting current are zer o. 5. Conclusion An innovative controllable reactor, side-limes and side-yokes magnetic-saturation type controlla ble reactor (SSMCR) is introduced in the paper.  X. Jin et al. Figure 11. Simulink schematic diagram of system. Figure 12. Control result of PID controller. A control system with PID controller and DC-DC converter is designed, and a PID self-tuning algorithm is proposed. At first, in algor ithm simulation, when the sudden changes of input o ccurs, conventional PID control- ler gives long adaption time (0.91 s) and big overshoot (7.3% of input variation), while the adaption time and overshoot of self-tuning PID algorithm is 0.13 s and zero. After that loads and compensation capacitor of system are calculated in Matlab to build the system model. Finally, the simulation based on the system model indicates that SSMCR with sel f-tuning PID algorithm can efficiently reduce the adaption time to 0.08 s and overshoot to zero. In conclusion, the control system we designed can control SSMCR with quick response and perfect smoothness.  X. Jin et al. Figure 13. DC exciting current curve. Since the control system and power grid model are simulated successfully, the experiments will be conducted in next stage based on t he simulation data. References [1] Wan g, H. (2007) Steady-State Analysis of Power Systems (3rd Vers i o n ). China Electric Power Press, Beijing. [2] Ti an , M.X., Li, Q.F. and Wan g, S.H. (20 02) An Equivalent Physical Model and a Mathematical Model of the Con- trolled Saturable Rreactor. Transactions of China Electrotechnical Society, 17, 18-21. [3] Feng, G.H., Wang, F.X. and Jin, W. (2001) Design Principles of Magnetically Controlled Reactor. Electrical Machines and Systems, 2001. Proceedings of the 5th International Conference on IEEE, 1, 212-214. [4] Zhang, G.Q. and Li, K. (2012) High -Voltage Single Phase Controlled Saturable Rreactor. [5] Astrom Karl, J. and Hagglu n d, T. (2006) Advancaed PID Control. ISA. [6] Sh en, Y.F., Wu, S.J. and Den g , F.L. (20 02) A Survey of Intelligent PID Control. Industrial Instrumentation & Auto- mation, 6, 11-24. [7] Man, K.F., Chen, G.R. and Kwong, S. (2001) An Optimal Fuzzy PID Controller. IEEE Transactions on Industrial Electro nics, 48 , 757 -765. [8] Cao, J.-Y., Lian g, J. and C ao, B.-G. (2005) Optimization of Fractional Order PID Controllers Based on Genetic Algo- rithms. Proceedings of 2005 International Conference, Guangzhou, 18-21 August 2005, 9, 5686-56 89. [9] S.-J. Li and Y.-X. Liu (2011 ) An Improved Approach to Nonlinear Dynamical System Identification Using PID Neural Networks. International Journal of Nonlinear Sciences and Numerical Simulation, 7, 177-182 .
|