HEALTH, 2009, 1, 17-23
Published Online June 2009 in SciRes. http://www.scirp.org/journal/health
Incorporating heterogeneous biological data sources in
clustering gene expression data
Gang-Guo Li1, Zheng-Zhi Wang1
1Institute of Automation, National University of Defense Technology, Changsha 410073, Hunan, China
Received 13 April 2009; revised 13 May 2009; accepted 14 May 2009.
ABSTRACT
In this paper, a similarity measure between
genes with protein-protein interactions is pro-
posed. The chip-chip data are converted into the
same form of gene expression data with pear-
son correlation as its similarity measure. On the
basis of the similarity measures of protein-
protein interaction data and chip-chip data, the
combined dissimilarity measure is defined. The
combined distance measure is introduced into
K-means method, which can be considered as
an improved K-means method. The improved
K-means method and other three clustering
methods are evaluated by a real dataset. Per-
formance of these methods is assessed by a
prediction accuracy analysis through known
gene annotations. Our results show that the
improved K-means method outperforms other
clustering methods. The performance of the
improved K-means method is also tested by
varying the tuning coefficients of the combined
dissimilarity measure. The results show that it is
very helpful and meaningful to incorporate het-
erogeneous data sources in clustering gene
expression data, and those coefficients for the
genome-wide or completed data sources should
be given larger values when constructing the
combined dissimilarity measure.
Keywor ds: statistical analysis; similarity/dissimilarity
measure; gene expression data; clustering; data
fusion
1. INTRODUCTION
With the rapid development of microarray technology in
the past few years, it is possible to monitor the expres-
sion levels of thousands of genes simultaneously [1].
Data from microarray experiments are denoted as a ma-
trix of genes by experimental conditions, where the con-
ditions are usually either a set of tissues or consecutive
time points in some environmental changes. The amount
of microarray data is very large. And microarray data are
mostly very redundant since many genes do not work
alone but are expressed together and interact to each
other. Thus, it is important to analyze the gene expres-
sion data.
Various clustering methods have been applied to the
analysis of gene expression data. Hierarchical clustering
[2] method becomes one of the most widely used tech-
niques for the analysis of gene expression data with the
advantages of simplicity and visualization of the results.
K-means clustering [3] is a good alternative to hierar-
chical clustering method when there is some prior
knowledge about the number of the clusters hidden in
the data. Hierarchical clustering and K-means clustering
are both global clustering methods which use the full set
of dimensions to measure the similarity and construct the
same global feature space for all clusters, and therefore
these clustering methods are likely to fail when they are
used for high dimensional data. Many researchers at-
tempted to solve this problem by different methods.
Self-Organizing Map (SOM) method was introduced to
interpret the patterns of gene expression [4]. Principle
component analysis method as a feature transformation
technique was used to preprocess expression data [5].
Support Vector Machine (SVM) method was also widely
used to identify sets of genes due to its good learning
performance for high dimensional data [6,7].
However, with the development of various genomic
knowledge resources (e.g., characterized protein-protein
interactions, functional annotations based on Gene On-
tology (GO), and transcription factors binding sites),
there comes a need to integrate the gene expression data
with these genomic knowledge resources for finding
some patterns with more biologically meaning.
In the recent years, some researchers have done some
work on the combination of gene expression data with
some prior knowledge. Reference [8] proposed the con-
struction of distance function which combines informa-
tion originating from microarray assays and biological
networks. The derived distance function was used fur-
ther to perform joint clustering of genes and vertices of
the network. Reference [9] introduced a machine learn-

18 G. G. Li et al. / HEALTH 1 (2009) 17-23
SciRes Copyright © 2009 HEALTH
ing approach to information fusion which allows inte-
gration of heterogeneous genomic data. Their procedure
may be seen as a generalization of well-known SOM
algorithm. Reference [10] defined a dissimilarity meas-
ure for GO knowledge, and combined GO knowledge
with gene expression data. They introduced their com-
bined dissimilarity measure into Partitioning Around
Medoids (PAM) [11] algorithm. In this paper we propose
a general framework to combine the gene expression
data with heterogeneous genomic knowledge resources
in order to enhance biological relevance of clustering
gene expression data.
2. DATA SOURCES
2.1. Protein-Protein Interactions Databases
Protein-protein interactions assemble the molecular ma-
chines of the cell and underlie the dynamics of virtually
all cellular responses, while genetic interactions reveal
functional relationships between and within regulatory
modules [6]. The sum of all such interactions defines the
global regulatory network of the cell. Proteomic and
functional genomics platform technologies now generate
large datasets of protein and genetic interactions, but
these datasets vary widely in coverage, data quality, an-
notation and availability. And so there are many different
interaction databases such as BioGRID [12], DIP [13],
BIND [14], MINT [15], and MIPS [16]. We use the data
of BioGRID for our research. BioGRID is a general re-
pository for interaction datasets. The recent version
2.0.34 release of BioGRID is a fully integrated cross-
species database that supports most major model organ-
isms, with increased data content and improved func-
tionality.
2.2. Chip-Chip Data
Chip-chip data are transcription factor-DNA binding
data that are generated as a result of the chip-chip assay
technique. This technique is used to determine whether
proteins including transcription factors will bind to par-
ticular regions of the chromatin within living cells. Two
genome-wide chip-chip data sources produced by the
technique are now available. One contains information
regarding the binding of 106 yeast transcription factors
[17]. The other one is a similar yeast dataset for a larger
number of transcription factors [18]. Both the data
sources are represented in the form of a confidence value
(statistical p-value) of a transcription factor attaching to
the promoter region of a gene. We use the chip-chip data
source with a larger number of yeast regulators for our
research, which contains information regarding the
binding of 203 regulators to their respective target genes
in rich medium. Besides rich medium, 84 regulators are
profiled in at least one environmental condition other
than rich medium.
3. METHOD
3.1. Similarity Measure between Genes with
Protein-Protein Interactions
Firstly we transfer protein-protein interactions into an
interaction matrix. For the whole gene set, which has N
genes, the interaction matrix is a N×N matrix M. If there
is an interaction between two different genes, gene i and
gene j, Mij=1. If there is no interaction between two dif-
ferent genes, gene i and gene j, Mij=0. And a gene i al-
ways can be considered as having an interaction with
itself, so Mii=1.
And then the similarity between genes with protein-
protein interactions could be calculated as follows:


N
j
ij
ij
PIPji
M
M
ggsimilarity
1
),( (1)
3.2. Similarity Measure of Gene Expression
Data
There are many ways to measure similarity between gene
expression data. We choose the pearson correlation to
represent similarity between gene expression data. And
the pearson correlation, rexpr, is expressed as follows:







M
i
M
i
ii
M
i
ii
r
vvuu
vvuu
r
11
22
1
exp
)()(
))((
(2)
Here, and denote the expression levels of
gene expression data and at experimental condi-
tion i, respectively. M is the total number of the experi-
mental conditions.
i
ui v
uv
u and v are the mean values of
the expression levels of and , respectively. uv
3.3. Similarity Measure of Chip-Chip Data
Suppose the chip-chip data represent the binding affinity
of transcription factors to promoters of each of
genes. If is the p-value for rejecting the null-hy-
pothesis that transcription factor does not bind the
promoter of gene , we define the binding score of tran-
scription factor to promoter of gene as
NT
ij
p
/)pij
j
i
j
p
i
)log(log( min xij

, where is the minimum
of all p-values.
min
p
,),, 21 iixx(iN x
i
x

denotes the
complete binding profile for gene i. By doing so, the
chip-chip data are presented in the same form of gene
expression data. Thus we use the pearson correlation as
the similarity measure for the chip-chip data.
3.4. Combined Dissimilarity Measure
If similarity measure has been defined, dissimilarity

G. G. Li et al. / HEALTH 1 (2009) 17-23 19
SciRes Copyright © 2009 HEALTH
measure can be calculated on the basis of similarity
measure. In this paper we calculated dissimilarity meas-
ure as follows:
simdis 1 (3)
Here, and mean the dissimilarity and
similarity measure respectively. We propose to combine
gene expression data with protein-protein interaction
data and chip-chip data. So the combined dissimilarity
measure can be expressed as follows:
dis sim
PIPchiprcom disdisdisdis 32exp1



(4)
Here, , and are the dissimi-
larity measures for gene expression data, chip-chip data
and protein-protein interaction data respectively. They
are all assumed to take values in [0,1]. Coefficients
r
disexp chip dis PIP
dis
1

,
2

and 3

present the weights of different dissimilar-
ity measures in the combined dissimilarity measure.
Thus they should satisfy: λ1+2

+3

=1 and they are
tuning parameters from [0,1]. Coefficients 2

and 3

quantify the influence of chip-chip and protein-protein
interactions knowledge on the clustering process. Note
that 1

=1, 2

=0 and 3

=0 means that the clustering is
decided only by gene expression data.
3.5. Annotation Prediction by Cluster
Analysis
Annotation prediction of novel genes is one of the initial
and useful applications for gene clustering results. Intui-
tively if an unexpectedly large number of genes in a
cluster belong to a specific functional category ‘F’, then
genes in this cluster are more likely to be relevant to
function ‘F’. Suppose a total of G genes in the genome
are analyzed in the microarray experiment among which
m genes are known to belong to a particular functional
category ‘F’. Within a cluster of size D genes, h genes
belong to the functional category ‘F’. Under the null
hypothesis that annotated genes are randomly distributed
in clusters, h follows a hypergeometric distribution [19].
The p-value (i.e. the probability of observing h or more
annotated genes in the cluster) is calculated as:


























 
m
G
im
DG
i
D
hXPh
i
1
0
1][ (5)
Intuitively unexpected large h will result in small p-
value indicating that majority of the genes in the cluster
might belong to the functional category ‘F’. Given a
pre-defined threshold Δ which is determined after multi-
ple comparison correction, all genes in the cluster are
assigned (predicted) to ‘F’ if its p-value is less than Δ. It
is noted that a cluster can be annotated to more than one
functional category by this procedure.
3.6. Knowledge-Based Cluster Evaluation
Many methods for cluster evaluation have been proposed
in the recent years. Reference [20] presented a survey of
cluster validation techniques including internal and exter-
nal indices and also explained specific biases intrinsic for
different evaluation measures. Among these methods there
are some utilizing annotations as the basis of knowl-
edge-based assessment. Reference [21] introduced a
knowledge-driven cluster evaluation method based on va-
lidity indices that incorporate similarity knowledge origi-
nating from the GO. Reference [22] also gave a cluster
evaluation method on the basis of pooling results from
various cluster number K and calculating functional pre-
diction accuracy according to the functional annotated
genes belonging to M known distinct functional categories.
In this paper, we use the knowledge-based cluster evalua-
tion method of [22], so that we avoid the problem of esti-
mating of the cluster number K.
As described in [22], the prediction accuracy of a
clustering method for a given p-value threshold Δ is de-
fined as:


 KK
KKPMVPA )(/)()( (6)
Here, A(Δ) means the prediction accuracy under the
given p-value threshold Δ, VPK(Δ) is the total number of
functional annotated genes under a given K which are as-
signed to the correct functional category and whose p-
values are smaller than Δ, and PMK(Δ) is the total number
of the gene number of the clusters under a given K which
have those functional annotated genes assigned to the cor-
rect functional category with smaller p-values than Δ.
4. REAL DATASET EXAMPLE
4.1. Dataset
We used the yeast cell-cycle data [23] which had listed
six known disjoint functional categories containing 104
genes. After we preprocessed and filtered the cell-cycle
data, we had 1703 genes left in which 86 genes belong to
the six known disjoint functional categories. Missing
values of the 1703 genes were imputed by LSimpute
method [24] and then the data of 1703 genes were nor-
malized. The yeast protein-protein interactions database
was downloaded from BrioGRID (http://www.thebiogrid.
org/downloads.php). The yeast database has 93122 pro-
tein-protein interactions. We neglected the differences
between one directional interaction and two directional
interactions and discarded any interactions involving
protein with itself. Then 50434 protein-protein interactions
were left. Among the 50434 protein-protein interactions,
only those interactions, whose two interacting genes were
both among the 1703 genes, were retained. Finally 3604
protein-protein interactions were obtained. The chip-chip
data was downloaded form the website [25].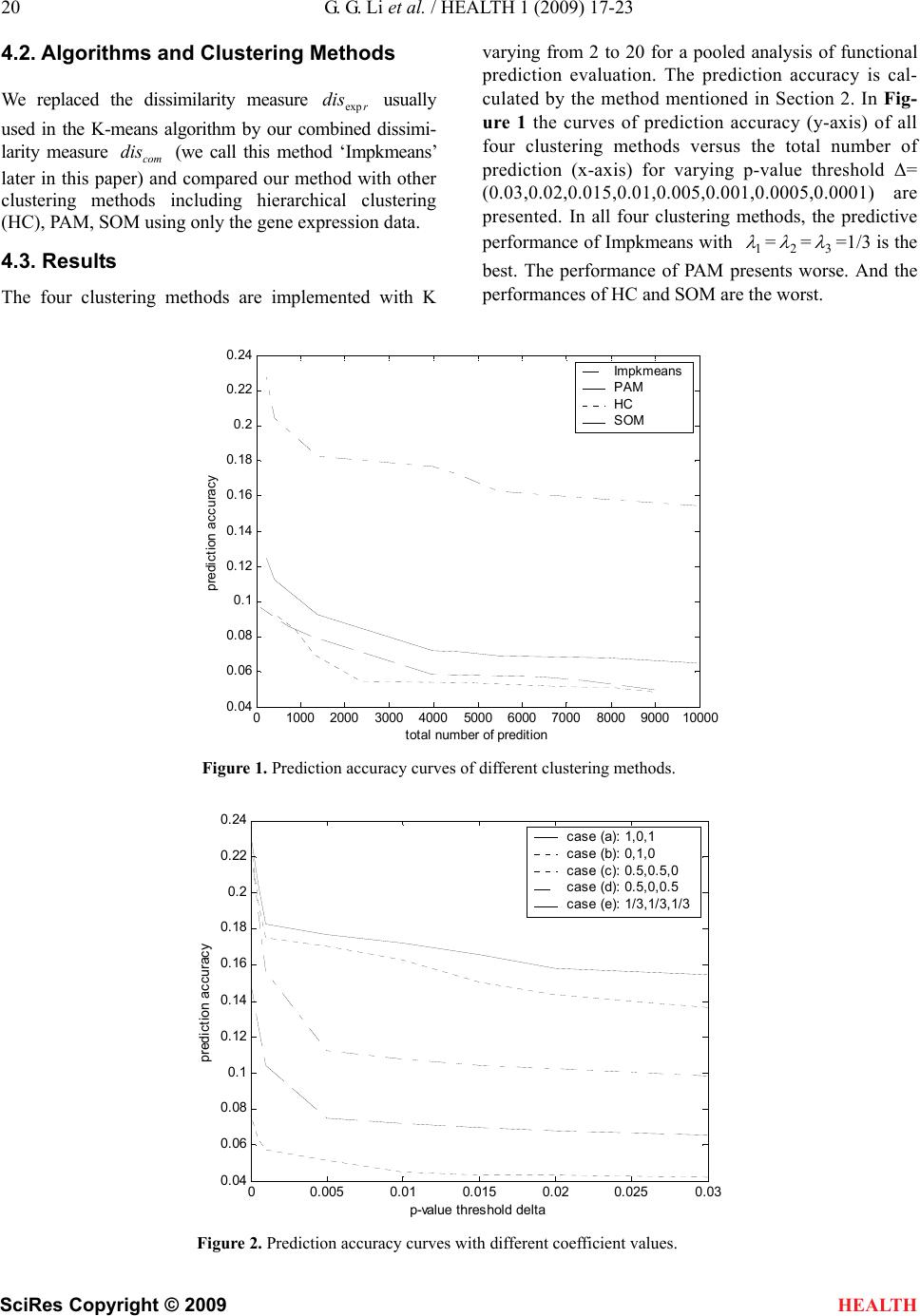

20 G. G. Li et al. / HEALTH 1 (2009) 17-23
SciRes Copyright © 2009
varying from 2 to 20 for a pooled analysis of functional
prediction evaluation. The prediction accuracy is cal-
culated by the method mentioned in Section 2. In Fig-
ure 1 the curves of prediction accuracy (y-axis) of all
four clustering methods versus the total number of
prediction (x-axis) for varying p-value threshold Δ=
(0.03,0.02,0.015,0.01,0.005,0.001,0.0005,0.0001) are
presented. In all four clustering methods, the predictive
performance of Impkmeans with 1

=2

=3

=1/3 is the
best. The performance of PAM presents worse. And the
performances of HC and SOM are the worst.
4.2. Algorithms and Clustering Methods
We replaced the dissimilarity measure usually
used in the K-means algorithm by our combined dissimi-
larity measure (we call this method ‘Impkmeans’
later in this paper) and compared our method with other
clustering methods including hierarchical clustering
(HC), PAM, SOM using only the gene expression data.
r
disexp
com
dis
4.3. Results
The four clustering methods are implemented with K
01000 2000300040005000 600070008000 900010000
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0.22
0.24
total number of predition
prediction accuracy
Impkmeans
PAM
HC
SOM
Figure 1. Prediction accuracy curves of different clustering methods.
00.005 0.01 0.015 0.02 0.025 0.03
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0.22
0.24
p-value threshold delta
prediction accuracy
case (a): 1,0,1
case (b): 0,1,0
case (c): 0.5,0.5,0
case (d): 0.5,0,0.5
case (e): 1/3,1/3,1/3
Figure 2. Prediction accuracy curves with different coefficient values.
HEALTH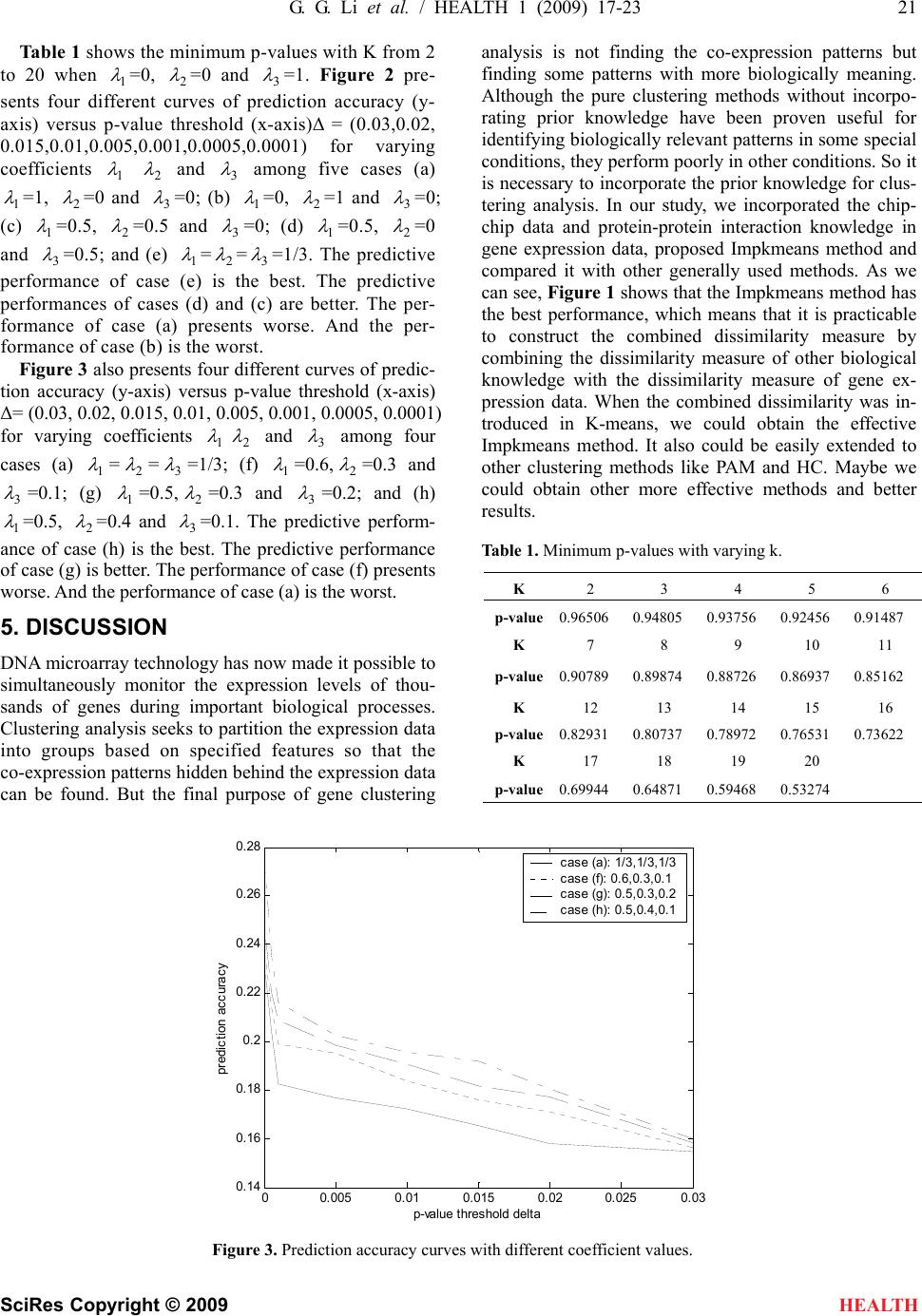

G. G. Li et al. / HEALTH 1 (2009) 17-23 21
SciRes Copyright © 2009 HEALTH
Table 1 shows the minimum p-values with K from 2
to 20 when 1

=0, 2

=0 and 3

=1. Figure 2 pre-
sents four different curves of prediction accuracy (y-
axis) versus p-value threshold (x-axis)Δ = (0.03,0.02,
0.015,0.01,0.005,0.001,0.0005,0.0001) for varying
coefficients 1

2

and 3

among five cases (a)
1

=1, 2

=0 and 3

=0; (b) 1

=0, 2

=1 and 3

=0;
(c) 1

=0.5, 2

=0.5 and 3

=0; (d) 1

=0.5, 2

=0
and 3

=0.5; and (e) 1

=2

=3

=1/3. The predictive
performance of case (e) is the best. The predictive
performances of cases (d) and (c) are better. The per-
formance of case (a) presents worse. And the per-
formance of case (b) is the worst.
Figure 3 also presents four different curves of predic-
tion accuracy (y-axis) versus p-value threshold (x-axis)
Δ= (0.03, 0.02, 0.015, 0.01, 0.005, 0.001, 0.0005, 0.0001)
for varying coefficients 1

2

and 3

among four
cases (a) 1

=2

=3

=1/3; (f) 1

=0.6, 2

=0.3 and
3

=0.1; (g) 1

=0.5,2

=0.3 and 3

=0.2; and (h)
1

=0.5, 2

=0.4 and 3

=0.1. The predictive perform-
ance of case (h) is the best. The predictive performance
of case (g) is better. The performance of case (f) presents
worse. And the performance of case (a) is the worst.
5. DISCUSSION
DNA microarray technology has now made it possible to
simultaneously monitor the expression levels of thou-
sands of genes during important biological processes.
Clustering analysis seeks to partition the expression data
into groups based on specified features so that the
co-expression patterns hidden behind the expression data
can be found. But the final purpose of gene clustering
analysis is not finding the co-expression patterns but
finding some patterns with more biologically meaning.
Although the pure clustering methods without incorpo-
rating prior knowledge have been proven useful for
identifying biologically relevant patterns in some special
conditions, they perform poorly in other conditions. So it
is necessary to incorporate the prior knowledge for clus-
tering analysis. In our study, we incorporated the chip-
chip data and protein-protein interaction knowledge in
gene expression data, proposed Impkmeans method and
compared it with other generally used methods. As we
can see, Figure 1 shows that the Impkmeans method has
the best performance, which means that it is practicable
to construct the combined dissimilarity measure by
combining the dissimilarity measure of other biological
knowledge with the dissimilarity measure of gene ex-
pression data. When the combined dissimilarity was in-
troduced in K-means, we could obtain the effective
Impkmeans method. It also could be easily extended to
other clustering methods like PAM and HC. Maybe we
could obtain other more effective methods and better
results.
Table 1. Minimum p-values with varying k.
K 2 3 4 5 6
p-value 0.96506 0.94805 0.93756 0.92456 0.91487
K 7 8 9 10 11
p-value 0.90789 0.89874 0.88726 0.86937 0.85162
K 12 13 14 15 16
p-value 0.82931 0.80737 0.78972 0.76531 0.73622
K 17 18 19 20
p-value 0.69944 0.64871 0.59468 0.53274
00.005 0.01 0.015 0.02 0.0250.03
0.14
0.16
0.18
0.2
0.22
0.24
0.26
0.28
p-value threshold delta
prediction accuracy
case (a): 1/3,1/3,1/3
case (f): 0.6,0.3,0.1
case (g): 0.5,0.3,0.2
case (h): 0.5,0.4,0.1
Figure 3. Prediction accuracy curves with different coefficient values.

22 G. G. Li et al. / HEALTH 1 (2009) 17-23
SciRes Copyright © 2009 HEALTH
As we can see in Table 1, the minimum p-values with
K varying from 2 to 20 are all far bigger than the p-value
threshold Δ used in our study. It shows that when 1

=0,
2

=0 and 3

=1, all the 86 annotation genes are clus-
tered in one cluster and this result has no biological sig-
nificance. This is partially because the interactions be-
tween proteins are complicated and one protein may
have many different interactions with different proteins.
As shown in Figure 2, the performance of cases (a) is
worse than those of cases (c), (d) and (e), which con-
firms that only using gene expression data is not enough
to infer more biologically meaningful patterns. That is to
say, incorporating some prior knowledge in clustering
gene expression data is helpful to obtain some more
biologically meaningful clusters. The performances of
cases (c) and (d) are worse than that of case (e), which
indicates that the more heterogeneous biological data
sources are incorporated in clustering gene expression
data, the better the result is. The prediction accuracy of
case (a) is higher than that of case (b), which implies that
the value of coefficient 1

should be larger than that of
2

when chip-chip data is combined with gene expres-
sion data. The prediction accuracy of case (c) is higher
than that of case (d), which implies that the value of co-
efficient 2

should be larger than that of 3

when
chip-chip data and protein-protein interaction data are
incorporated in clustering gene expression data.
As shown in Figure 3, the prediction accuracy
changes with varying the proportion of coefficients 1

,
2

and 3

. The performance of case (a) is worse than
that of other cases in Figure 3, which indicates the im-
portant levels of the three data sources are not the same
for constructing the combined dissimilarity measure, and
better results are obtained when the ratios of coefficient
1

to other coefficient are higher than 1. However, it is
not that the larger the ratios of coefficient 1

to other
coefficients are, the better the results are. This is proved
by the better results of case (g) compared with case (f)
(the ratios of 1

to 2

and 3

in case (g) are 2 and 6
respectively, while the ratios of 1

to 2

and 3

in
case (g) are 5/3 and 2.5). That is to say, the influence of
biological data sources on detecting biologically mean-
ingful clusters should not be neglected though the gene
expression data are the most important. Otherwise, the
performance of case (h) is better than case (g), which
shows that different biological data sources have differ-
ent important levels and the important level of chip-chip
is higher than that of protein-protein interaction data.
This is partially because that the chip-chip data is a ge-
nome-wide data source while protein-protein interaction
data is a partial data source.
In general, it is very helpful and meaningful to incor-
porate heterogeneous data sources in clustering gene ex-
pression data, and those coefficients for the genome- wide
or completed data sources should be given larger values
when constructing the combined dissimilarity measure.
6. CONCLUSIONS AND FUTURE
RESEARCH
The similarity measures for protein-protein interaction
and chip-chip data were constructed by transforming the
presentation forms of these data. They are combined
with the similarity measure for gene expression data
under a general framework. The combined similarity
measure was used to enhance the K-means method, with
which the gene patterns with more biologically meaning
were produced. This presents that our framework is use-
ful for clustering gene expression data to incorporating
heterogeneous biological data sources.
Otherwise, our general framework can be extended.
As we can see in (4), the combined dissimilarity measure
could be extended from the sum of three different dis-
similarity measures to the sum of M different dissimilar-
ity measures:
),(),(
1
jim
M
m
mjicomb ggdisggdis 

  (7)
Here, dism refers to m-th dissimilarity measure and
coefficient {λm}m=1,…,M satisfy: λ1+…+λM=1.
The dism may be a dissimilarity measure of some other
gene expression data, or may be a user defined dissimi-
larity measure of some other prior knowledge such as
GO, protein binding sites knowledge, and protein-DNA
interaction knowledge. For different research purpose,
choosing different gene expression data and different prior
knowledge, and fusing all these information together
when carrying out the clustering work, we could expect
that more biologically meaningful results would come.
7. ACKNOWLEDGEMENT
The authors thank Dr. Yaohua Du for valuable discussions. And the
authors are very grateful to the anonymous referees who gave us help-
ful comments which improved the quality of this paper. This work is
partly supported by the National Nature Science Foundation of China
under Grant No. 60835005.
REFERENCES
[1] D. Lockhart and E. Winzeler, (2000) Genomics gene
expression and DNA arrays, Nature, 405, 827-846.
[2] M. B. Eisen, P. T. Spellman, P. O. Brown, and D.
Botstein, (1998) Cluster analysis and display of genome-
wide expression patterns, Proc. Natl Acad. Sci. USA, 95,
14863-14868.
[3] S. Tavazoie, J. D. Hughes, M. J. Campbell, R. J. Cho,
and G. M. Church, (1999) Systematic determination of
genetic network architecture, Nature Genetics, 22,
281-285.

G. G. Li et al. / HEALTH 1 (2009) 17-23 23
SciRes Copyright © 2009 HEALTH
[4] P. Tamayo, D. Slonim, J. Mesirov, Q. Zhu, S.
Kitareewan, E. Dmitrovsky, E. S. Lander, and T. R.
Golub, (1999) Interpreting patterns of gene expression
with self-organizing maps: Methods and application to
hematopoietic differentiation, Proc. Natl Acad. Sci. USA,
96, 2907–2912.
[5] S. Raychaudhuri, J. M. Stuart, and R. B. Altman, (2000)
Principal component analysis to summarize microarray
experiments: Application to sporulation time series, Pac.
Symp. Biocomput., 455–466.
[6] M. P. Brown, W. N. Grundy, D. Lin, N. Cristianini, C. W.
Sugnet, T. S. Furey, M. Jr. Ares, and D. Haussler, (2000)
Knowledge-based analysis of microarray gene expression
data by using support vector machines, Proc. Natl Acad.
Sci, 97, 262–267.
[7] H. Xia, A. Panaye, and B. T. Fan, (2007) Nonlinear SVM
approaches to QSPR/QSAR studies and drug design,
Current Computer-Aided Drug Design, 3, 341–352.
[8] D. Hanisch, A. Zien, R. Zimmer, and T. Lengauer, (2002)
Coclustering of biological networks and gene expression
data, Bioinformatics, 18, 145–154.
[9] J. Kasturi and R. Acharya, (2005) Clustering of diverse
genomic data using information fusion, Bioinformatics,
21, 423–429.
[10] K. Rafal and Z. Adam, (2006) Incorporating gene
ontology in clustering gene expression data, CBMS’06.
[11] L. Kaufman and P. Rousseeuw, (1990) Finding groups in
data: An introduction to cluster analysis, Wiley, New York.
[12] S. Chris, B. Bobby-Joe , R. Teresa, B. Lorrie, B. Ashton,
and T. Mike, (2006) BioGRID: A general repository for
interaction datasets, Nucleic Acids Research, Database
issue, 34, D535–D539.
[13] X. loannis, F. Esteban, S. Lukasz, D. Xiaoqun, T.
Michael, M. Edward, and E. David, (2001) DIP: The
database of interacing proteins: 2001 update, Nucleic
Acids Research, 29, 239–241.
[14] C. Alfarano, C. E. Andrade, K. Anthony, N. Bahroos, M.
Bajec, K. Bantoft, D. Betel, B. Bobechko, K. Boutilier,
and E. Burgess, (2005) The biomolecular interaction
network database and related tools: 2005 update, Nucleic
Acids Res., 33, D418–D424.
[15] A. Zanzoni, L. Montecchi-Palazzi, M. Quondam, G.
Ausiello, M. Helmer-Citterich, and G. Cesareni, (2002)
MINT: A molecular INTeraction database, FEBS Lett.,
513, 135–140.
[16] H. W. Mewes, C. Amid, R. Arnold, D. Frishman, V.
Guldener, G. Mannhaupt, M. Munsterkotter, P. Pagel, N.
Strack, and V. Stumpflen, (2004) MIPS: Analysis and
annotation of proteins from whole genomes, Nucleic
Acids Res, 32, 41–44.
[17] C. T. Harbison, D. B. Gordon, T. I. Lee, N. J. Rinaldi, K.
D. Macisaac, T. W. Danford, N. M. Hannett, J. B. Tagne,
D. B. Reynolds, J. Yoo, et al., (2004) Transcriptional
regulatory code of a eukaryotic genome, Nature, 431,
99–104.
[18] T. I. Lee, N. J. Rinaldi, F. Robert, D. T. Odom, Z.
Bar-Joseph, G. K. Gerber, N. M. Hannett, C. T. Harbison,
C. M. Thompson, I. Simon, et al., (2002) Tanscriptional
regulatory networks in Saccharomyces cerevisiae,
Science, 298, 799–804.
[19] S. Tavazoie, J. D. Hughes, M. J. Campbell, R. J. Cho,
and G. M. Church, (1999) Systematic determination of
genetic network architecture, Nature Genetics, 22,
281–285.
[20] J. Handl, J. Knowles, and D. Kell, (2005) Computational
cluster validation in post-genomic data analysis,
Bioinformatics, 21, 3201–3212.
[21] N. Bolshakova, F. Azuje, and P. Cunningham, (2005) A
knowledge-driven approach to cluster validity
assessment, Bioinformatics, 21, 2546–2547.
[22] A. Thalamuthu, M. Indranil, X. J. Zeng, and G. C. Tseng,
(2006) Evaluation and comparison of gene clustering
methods in microarray analysis, Bioinformatics, 22,
2405–2412.
[23] P. T. Spellman, G. Sherlock, M. Q. Zhang, V. R. Iyer, K.
Anders, M. B. Eisen, P. O. Brown, D. Botstein, and B.
Futcher, (1998) Comprehensive identification of cell
cycle-regulated genes of the yeast Saccharomyces
cerevisiae by microarray hybridization, Mol. Biol. Cell, 9,
3273–3297.
[24] B. Trond, D. Bjarte, and J. Inge, (2004) LSimpute:
accurate estimation of missing values in microarray data
with least squares methods, Nucleic Acids Research,
32(3).
[25] Young Lab, http://web.wi.mit.edu/young/regulatory_
code.