Novel Joint Chip Sampling and Phase Synchronization Algorithm for Multistandard UMTS Systems

doi:10.4236/ijcns.2008.12014

I. J. Communications, Network and System Sciences, 2008, 2, 105-206

Published Online May 2008 in SciRes (http://www.SRPublishing.org/journal/ijcns/).

Novel Joint Chip Sampling and Phase Synchronization

Algorithm for Multistandard UMTS Systems

Youssef SERRESTOU1, Kosai RAOOF2, Joël LIÉNARD2

1 LCIS-INPG, 50 Rue Barthélémy de Laffemas, 26902 cedex, Valence, France

2 GIPSA-LAB, CNRS UMR 5216, 961 Rue de Houille Blanche, 38402 St. Martin d’Hères, France

E-mail: 1youssef.serrestou@esisar.inpg.fr, 2kosai.raoof@gipsa-lab.inpg.fr

Abstract

CDMA Timing and phase offsets tracking remain as one of considerable factors that influence the

performances of communication systems. Many algorithms are proposed to solve this problem. In general,

these solutions process separately the chip sampling offset and phase rotation. In addition, most of proposed

solutions can not assure a compromise between robustness criteria and low complexity for implementation in

real time applications. In this paper we present an efficient algorithm for chip sampling and phase

synchronization. This algorithm allows estimating and correcting jointly in real time, sampling instant and

phase errors. The robustness and the low complexity of this algorithm are evaluated, firstly by simulation

and then tested by real experimentation for UMTS standard. Simulation results show that the proposed

algorithm provides very efficient compensation for sampling clock offset and phase rotation. A real time

implementation is achieved, based on TigerSharc DSP, while using a complete UMTS transmission-

reception chain. Experimental results show robustness in real conditions.

Keywords: Synchronization, DS-CDMA, UMTS, Joint Estimation, Early-late Loop, Phase Locked Loop

1. Introduction

Code Division Multiple Access (CDMA) system offers

several advantages such as robustness to multi-path

fading channel and multiple access properties [1].

Thanks to these advantages, CDMA are adopted in high

data rate applications such as UMTS standard (Universal

Mobile Telecommunication System), and it is a good

candidate for future applications, such as the 4th

generation phone mobile and wireless LAN [2].

However, the performance of such systems is affected

by the time sampling offsets and phase rotation, due to

many factors such as channel fading, multipath problem,

clock imperfection, etc.

Recent research works are interested in solving this

problem of synchronization for different applications [3–

7]. In general the synchronization techniques of DS-

CDMA systems can achieve synchronization in two

distinct steps: acquisition step and tracking step. The

acquisition step, or the initial synchronization step,

involves in determining the timing/phase offsets of the

incoming signal to within a specified range known as the

pull-in region of tracking loop [8–11]. Upon the

successful completion of the acquisition step, the

tracking step refines and maintains synchronization.

When the problem of tracking is treated, generally,

phase offset tracking is omitted or treated separately

with a more complex computation than delay tracking

[3–7, 12, 13]. The tracking step is based on recursive

estimation of timing/phase error and feedback correction.

So the performance of synchronization depends greatly

on the properties of estimators and on the precision of

correctors. To estimate time delay the conventional

delay lock loop (DLL) has been extensively used. In a

DLL the received signal is cross-correlated with an early

and a late copy of a pilot signal. The proposed tracking

algorithm is inspired from the concept of lock loop to

establish estimation [14]. So the complex correlation

function of the received signal and pilot signal is

computed in three points (which corresponds to original,

early and late copy of the pilot signal). This computation

allows estimating jointly the time delay and the phase

rotation. A second order filters are used to update the

estimation. For the feedback corrector, an interpolator

[15] is used to find the sample at the estimated instant;

106 Y. SERRESTOU ET AL.

the used interpolator gives good compromises between

precision and real time application. The correction of

phase rotation consists of multiplying the received signal

by the complex exponential of estimated phase [14,15].

In this study we are interested in implementing the

tracking algorithm in a complete transmission-reception

chain. The aim of this chain is to demonstrate the

feasibility of a reconfigurable software radio

communication system based on UMTS standard. The

tracking algorithm was adapted to UMTS specifications

[16–20]. In simulation context, the performances of

these algorithms were evaluated in the presence of a

fading and additive white Gaussian noise channel

(AWGN). In the case of a multipath channel, acquisition

and tracking blocks synchronize the signal of the high

power path. One block within the complete chain

contains an algorithm for channel estimation [21,22].

DS-CDMA was adopted in UMTS standard as an

access scheme. And for radio access there are two modes,

FDD (Frequency Division Duplex) and TDD (Time

Division Duplex), for operating with paired and

unpaired bands respectively. The possibility to operate

in either FDD or TDD mode allows an efficient use of

the available spectrum according to the frequency

allocation in different regions. The modulation scheme is

QPSK, and because of the CDMA nature the spreading

(and scrambling) process is closely associated with

modulation. To spread transmitted signal different

families of spreading codes are used. For separating

channels from the same source, orthogonal codes are

derived with code tree structure. And for separating

different cells in FDD mode Gold codes with 10 ms

period (38400 chips at 3.84 Mcps) are used and for TDD

mode we implement codes with period of 16 chips and

midamble sequences of different length depending on

the environment [16-20]. Our tracking algorithm has

adopted for both UMTS modes TDD and FDD.

Simulation has allowed evaluating the performances and

determining suitable parameters for implementation. The

final real time implementation was accomplished with a

32-bit TigerSharc DSP.

The rest of this paper is organised as follows. Section

2 presents the algorithm context. The basic aim of this

section is to present the theoretical models of

transmitted/received signals in UMTS and the

communication channel that we consider. So the

different phases of signal forming (spreading,

scrambling, channel effects, noise) are described. In

section 3, the mathematical model of the tracking

algorithm is presented, as well as it’s adaptation for

UMTS-FDD and UMTS-TDD standard. We focus on

the estimators’ performances with theoretical

demonstration ended by simulation to show the

efficiencies of this algorithm. Section 4 describes

simulation platform and result analysis. The

implementation and experiment results are detailed in

section 5. Some conclusions are given in section 6.

2. Base-Band Signal Model in UMTS

2.1. Introduction

Our tracking algorithm tries to maintain synchronization

of the received signal by a UMTS terminal. So we are

interested in the downlink mode (base station to

terminal). We introduce some useful notions for

modeling the base-band signal in the context of UMTS

standard. These notions are specified and described in

detail in the 3rd Generation Partnership Project (3GPP);

see [16–20].

The access scheme is Direct-Sequence Code Division

Multiple Access (DS-CDMA). There are two radio

access modes, FDD (Frequency Division Duplex) and

TDD (Time Division Duplex), which allows operating

with paired and unpaired bands respectively. The

modulation scheme is QPSK, and different families of

spreading codes are used. These codes are OVSF

(orthogonal variable spreading factor). And for

separating different cells in FDD mode Gold codes

(scrambling codes) with 10 ms period (38400 chips at

3.84 Mega chip per second Mcps) are used and for TDD

mode we use codes with period of 16 chips and

midamble sequences of different length depending on

the environment [16–20]. In FDD mode the uplink and

downlink transmissions use two different radio

frequencies. In TDD mode the uplink and downlink

transmissions are modulated over the same frequency by

using synchronized time intervals.

In both modes the transmitted signal is decomposed

into radio frames. A radio frame has duration of 10 ms

and contains 38400 chips at the rate of 3.84 Mcps. It is

divided into 15 slots, and every slot contains 2560 chips.

A physical channel is therefore defined as a simple

code (or number of codes used to spread this channel),

additionally in TDD mode the sequence of time slots

completes the definition of a physical channel.

The information rate, in terms of symbols/s, varies

with the spreading factor (number of chips by symbol).

Spreading factors (noted SF) are from 512 to 4 for FDD

downlink, and from 16 to 1 for TDD downlink. Thus the

respective modulation symbol rates vary from 960 k

symbols/s to 15 k 7.5 k symbols/s for FDD downlink,

and for TDD the momentary modulation symbol rates

shall vary from 38400 symbols/s to 240 k symbols/s.

2.2. Signal Model in UMTS-FDD Mode

In FDD mode a practical fixed rate channel with

predefined symbol (1+j) sequence is transmitted within

each frame, this common pilot channel (CPICH), use the

first spreading code in tree with spreading factor equal to

256. The proprieties of this channel allows receiver to

identify cell’s location. In our work we have used this

channel as signal pilot to estimate the time delay and

NOVEL JOINT CHIP SAMPLING AND PHASE SYNCHRONIZATION 107

ALGORITHM FOR MULTISTANDARD UMTS SYSTEMS

phase rotation.

Let N physical channels be transmitted with QPSK

symbols

{

}

jd n

l±±= 1

)( , n denotes the channel number

and l represents the symbol number.

Every symbol is transformed to a sequence of chips

by spreading operation. SF “spreading factor” denotes

the spreading code length, i.e. the number of chip per

symbol. The combination of all channels is scrambled by

the same code that we denoted SC. The following

combined signal is obtained:

))(()( ,

)(

ckSFlk

SF

k

n

SFk

N

l

n

l

N

n

nTSFlktSCCdGtd n

n

n⋅⋅+−= ⋅+

∑∑∑

δ

(1)

where G

n is the gain of channel n,

{

}

1,1

,−∈

n

SFk n

C is

the kth chips in spreading code used to spread the nth

channel, SFn is the spreading factor used for the nth

channel and

{}

1,1−∈

k

SC denotes the kth chip in

scrambling code. Tc is chip duration and δ(.) is the Dirac

delta function.

A root raised cosine impulse filter, denoted he(t), is

used to shape this signal for transmission.

For propagation channel, we adopt a fading channel

with AWGN noise. Its impulse response is modeled as

follow:

))(()()( )( ttetth tj

c

τδα ϕ

−= (2)

where α(t) is the fading of propagation channel given

from Jake’s Doppler spectrum, τ(t) is the time delay, and

φ(t) represents the random phase shift introduced by

propagation, and it will be added to another phase shift

which is caused by the imperfections of receiver-

transmitter oscillators.

The received signal is filtered by a root raised cosine

with impulse response hr(t). Then it is sampled with a

period Te. We denote by OSF=Tc/Te the over sampling

factor, i.e. number of samples per chip. Let g(t) be the

convolution product Cr0(t)*hc(t)*hr(t), the received

signal may be written as:

{}

)())()(()()( ,,

)(

,tmTTlSFkOSFttgSCCaGtety

n

kk

nSF

k

OSF

m

eeklSFk

n

SFk

N

l

nl

N

n

t

FDDr

ητα

ϕ

+−+−−= ∑∑∑∑ + (3)

{}

)())()(()()(

))256()(()1()()()(

,,

)(

0

256

)(

0,

tmTTlSFkOSFttgSCCaGtety

where

mTTlkOSFttgSCjGtetyty

n

kk

n

SF

k

OSF

m

eeklSFk

n

SFk

N

l

nl

N

n

t

r

CPICH

k

OSF

m

eelk

N

l

cpich

t

channelother

rFDDr

ητα

τα

ϕ

+−+−−=

−+−−++=

∑∑∑∑

∑∑∑

+

4444444444444434444444444444421

321

(4)

{

Noise

data

OSF

l

eee

N

ni

k

i

kk

n

midamble

OSF

l

eee

L

n

k

n

data

OSF

l

eee

N

ni

k

i

kk

n

tjk

TDDr

ttlTOSFnTOSFTitgswd

tlTOSFnTOSFTitgm

tlTOSFnTOSFTitgswdetty

k

m

k

)())(16)1((.

))(16)1((

))(16)1((.)()(

1

00

16

1

)2,(

1

01

1

00

16

1

)1,()(

,

ητ

τ

τα ϕ

+

⎥

⎦

⎤

−−−−−

+−−−−−

+

⎢

⎣

⎡

−−−−−=

∑∑∑

∑∑

∑∑∑

−

===

−

==

−

===

444444444444344444444444421

44444444443444444444421

444444444444344444444444421

(5)

where η(t) is an additive Gaussian noise, Te is the

sampling time (Tc=OSF.Te), Tc is the chip duration, and

φ(t) is the global phase shift introduced by propagation

channel and oscillators imperfections. In FDD the

received signal contains the CPICH symbols, so we can

separate the signal in two parts; one part contains CPICH

symbols and the other part contains the other transmitted

channels, which allows us to write equation (4).

Equation (4) gives us the received signal model in

baseband for UMTS-FDD, the calculus and

demonstrations in the next sections are based on this

model.

108 Y. SERRESTOU ET AL.

2.3. Signal Model in UMTS-TDD Mode

The UMTS TDD physical channel is a combination of

two data fields, a midamble, and a guard period. There

are two burst types proposed in [20], namely burst type 1

and 2. As illustrated in Figure 1, both types have the

same length of 2560 chips and are terminated by a guard

period of 96 chips in order to avoid overlapping with

consecutive time slots. Burst type 1 has a longer

midamble (512 chips) suitable for cases where long

training periods are required for adaptation and tracking.

The midamble code is used as signal pilot for tracking

algorithm.

Figure 1. Two burst types

With the same notation as the previous sub-section B,

the received signal in TDD modes will be written as

described in (4). In equation (4), d(k,1) denotes the data

symbols transmitted before the midamble and d(k,2)

denotes the data symbols after the midamble. The

combination of the user specific channelization and cell

specific scrambling codes can be seen as a user and cell

specific spreading code, with chip values, are denoted by

Si

k in (4).

3. Digital Joint Synchronization Algorithm

3.1. Introduction

The sampling instant of the received signal is fluctuated,

and the phase is shifted because of the channel effects,

the reception clock imperfections, and receiver-

transmitter oscillators’ imperfections. The received

signal needs synchronization to extract the transmitted

sequences. So that synchronization is divided into two

phases, acquisition phase and tracking phase.

Acquisition is the first step that the mobile phone does,

known as “cell search” in UMTS standard. It consists

finding the beginning of signal (top frame and top slot)

within a half chip precision. This operation allows also

finding the cell’s parameters. The tracking step updates

the phase and the sampling instant continuously in time.

In this section we will detail the algorithm used in

tracking phase. The developed algorithm consists of four

steps, as shown on Figure1, assuming that the baseband

signal is obtained by radio frequency down conversion

followed by a linear filtering system, and the acquisition

is done correctly.

3.2. Timing Correction

We look to extract from the received samples the correct

transmitted samples. To perform this operation the

received signal will be interpolated at the estimated

correct instant. The following formula presents the

fundamental equation for digital interpolation [23]:

[][]

⎥

⎦

⎤

⎢

⎣

⎡

=⇒+

⎥

⎦

⎤

⎢

⎣

⎡

=

+⋅−=+=∑

=

e

i

keke

e

i

ek

N

i

ekekki

T

kT

mTT

T

kT

TihTimxTmykTy

µ

µµ

)()())(()(

0

where x is the received signal, Te is the theoretical

sampling period, Ti represents the fluctuated sampling

period, and h(t) is the impulse response of interpolated

filter. The interpolation coefficients are modified in

function of the delay µk.

In our work we estimate the delay time µk then we

adapt the interpolator coefficients. N is the number of

interpolator coefficients, and [] denotes integer part

function.

In literature there are many methods to interpolate

digital signal: linear interpolation, polynomial

interpolation, piecewise-parabolic interpolation and

some others [23,24]. The choice of an interpolator

depends on two criterions: precision and complexity. In

our study we have chosen a truncated cardinal sine wave.

In UMTS the over-sampling factor is reconfigurable, and

to assure real time criteria the number of interpolators’

coefficients depends on the over-sampling factor.

3.3. Phase Correction

The second step is to correct the phase shift. The

interpolated complex samples (I and Q) are multiplied by

complex exponential of the estimate phase.

k

j

iiekTykTz

ϕ

ˆ

)()( −

=

where y(kTi) is the interpolated complex samples and k

ϕ

ˆ

is the estimated phase. For phase correction, in order to

find the phase reference, the sign of the real and

imaginary parts allows to find the reference region in the

QPSK plan.

3.4. Joint Estimation of Delay and Phase

Now we are arrived in one of the principal point in our

work, the correction of the sampling instant and phase

require the knowledge of time delay and phase shift. We

use a procedure that allows us estimating jointly these

parameters. These measurements are filtered by a loop

filters, then they are used by interpolation and phase

correction blocks. We use two different methods for

estimation in the TDD and FDD modes. In the following

NOVEL JOINT CHIP SAMPLING AND PHASE SYNCHRONIZATION 109

ALGORITHM FOR MULTISTANDARD UMTS SYSTEMS

sub-sections we explain these methods.

3.4.1. Estimation for UMTS-FDD Mode

The sampling instant delay and the phase shift are

estimated over one symbol duration, Ts=SF*Tc, in order

to correct the next symbol timing. The sampling instant

is corrected by interpolation and the phase is corrected

by complex multiplication between received signal and

estimated phase.

We use as a pilot signal the corresponding scrambling

code, because the CPICH channel is a copy of the

scrambling code. So the received signal is divided into

successive symbols (256 chips i.e. 256.OSF samples),

and we calculate the correlation between each symbol

and the original, early, and late copy of the

corresponding symbol.

Let yr,s be the sth symbol of received signal (described

in equation (4)) and SCs represents the sequence of

scrambling code, which was aligned in transmission with

this part of the signal. The time delay and phase shift are

supposed to be constant during one symbol period, then

without correction of signal we obtain the following

correlation function at instant ε:

{

}

{

Noise

ationautocorrel

SC

delay

SC

ssymbol

CPICH

cpich

shift

phasage

s

fading

SCy sjGes sssr )())(()1()()()(

'

_

)(

,

,0

ετεγαεγεγ ϕ

Ν+−++= 4434421

321

(6)

The spreading code is orthogonal, that means the

correlation function of two codes is equal to zero. The

first term is negligible. The scrambling code local auto-

correlation function can be approximated by a triangular

function:

c

sc T

ε

εγ

−≈ 1)(

For 2

,0,

2cc TT

−=

ε

we have:

)0()

)(

1)(1()(

)0())(()1()()0(

)(

=+−+≈

=+−+≈=

ε

τ

α

εταε

ϕ

N

T

s

jGse

NsrjGser

c

cpich

s

SCcpich

s

r

)2/()

)(

2

1

1)(1()(

)2/())(

2

()1()()

2

(

)(

c

cpich

s

c

SCcpich

s

c

TN

T

s

jGse

TNs

T

rjGse

T

rr

−++−+≈

−+−−+≈−=

τ

α

ταε

ϕ

)2/()

)(

2

1

1)(1()(

)2/())(

2

()1()()

2

(

)(

c

cpich

s

c

SCcpich

s

c

TN

T

s

jGse

TNs

T

rjGse

T

rr

−+−−+≈

+−+≈=

τ

α

ταε

ϕ

(7)

We observe that these measurements contain

information about the time delay and the phase shift; our

idea is to extract this information from these

measurements. Real and imaginary parts of one-time

correlation function allow estimating the phase rotation

φ(s). The early and late correlation functions give

estimation of the time delay τ(s). Let define the

measurements ∆τ and ∆φ, as the sampling instant delay

and phase shift. And Re(.), Im(.) are the real and

imaginary part function of a complex number.

),()](sin[

)(

1)(2

))0(Im())0(Re()(,, ,,

τϕηϕ

τ

α

ε

ϕ

+

⎟

⎠

⎞

⎜

⎝

⎛−=

=−

=

∆

s

T

s

Gs

rrs

c

cpich

SCySCy ssrssr

),()](cos[

)(

2

1

1)(2

))

2

(Im())

2

(Re()(

1

,,1 ,,

τϕηϕ

τ

α

εε

+

⎟

⎠

⎞

⎜

⎝

⎛−−=

=+==∆

s

T

s

Gs

T

r

T

rs

c

cpich

c

SCy

c

SCy ssrssr

),()](cos[

)(

2

1

1)(2

))

2

(Im())

2

(Re()(

2

,,2 ,,

τϕηϕ

τ

α

εε

+

⎟

⎠

⎞

⎜

⎝

⎛−−=

−=+−==∆

s

T

s

Gs

T

r

T

rs

c

cpich

c

SCy

c

SCy ssrssr

⎪

⎩

⎪

⎨

⎧

+

⎟

⎠

⎞

⎜

⎝

⎛−−+≅

∆−∆=∆

+

⎟

⎠

⎞

⎜

⎝

⎛−≅∆

⇒

),()](cos[

)(

2

1)(

2

1

)(2

)(

),()(sin

)(

1)(2)(

2

21

1

τϕηϕ

ττ

α

τϕηϕ

τ

α

ϕ

s

T

s

T

s

Gs

s

T

s

Gss

cc

cpich

x

c

cpich

(8)

Let )(

ˆs

τ

be the estimation of the sampling instant

delay and )(

ˆs

ϕ

is the estimation of phase shift, with a

correction loop. Then the previous equations become:

⎪

⎩

⎪

⎨

⎧

+−

⋅

⎟

⎠

⎞

⎜

⎝

⎛−

−−

−

+≅∆

+

−

⎟

⎠

⎞

⎜

⎝

⎛−

−≅∆

),()](

ˆ

)(cos[

)()(

ˆ

2

1)()(

ˆ

2

1

)(2)(

),(

)](

ˆ

)(sin[

)()(

ˆ

1)(2)(

2

1

τϕηϕϕ

ττττ

α

τϕη

ϕϕ

ττ

α

ϕ

ss

T

ss

T

ss

Gss

ss

T

ss

Gss

cc

cpichx

c

cpich

(9)

If the system of estimation and correction converge

correctly, the time delay and phase error must converge

to zero. In this condition:

[

]

()

1)(

ˆ

)(cos

)(

ˆ

)()(

ˆ

)(sin

≈−

−≈

−

ss

ssss

ϕϕ

ϕ

With this condition, equation (8) gives the estimation

of delay and phase as follows:

[

]

),(

)()(

ˆ

)(4

)(

),()(

ˆ

)()(2)(

2

1

τϕη

ττ

α

τ

ϕ

η

ϕ

α

τ

ϕ

+

−

≅∆

+−

≅

∆

e

cpich

T

ss

OSF

Gs

s

ssGss

(10)

110 Y. SERRESTOU ET AL.

where OSF is the over sampling factor, i.e. the number

of samples per chip, Tc is the chip duration and Te is the

sampling period. Hence, Tc=OSF.Te. Gcpich is the channel

gain of CPICH [17,18], and α(s) is the fading of the

propagation channel. Always, we suppose that the fading

is invariant for symbol duration (Ts=SF.Tc=SF.OSF.Te).

These measurements are filtered by a second order filter

that we discuss it in the next section. Now we will

establish these measurements in the case of TDD mode.

3.4.2. Estimation for UMTS-TDD Mode

We are going here to explain how we estimate sampling

instant delay and phase shift in TDD mode. In this mode

we process slot by slot the 2560 chips i.e. 2560.OSF

samples. This is different from FDD mode where we

process symbol by symbol. We have chosen this way

because in the TDD mode we don’t have a permanent

channel with a known spreading code. In addition the

TDD mode will be used when we have a good

propagation channel conditions. In this case we can

consider that the delay time and the phase shift are

constant over one slot duration. For these raisons we use

midamble code as a signal pilot to achieve

synchronisation. So we calculate correlation function

between the received midamble and the transmitted

midamble in three points (codes aligned, the midamble

code shifted to right and to left by OSF/2 samples).

These measurements are filtered to estimate time delay

and phase shift. Estimation of the sampling instant delay

and the phase shift over actual slot is used to correct the

next slot. The sampling instant is corrected by

interpolation and the phase is corrected by complex

multiplication between received signal and complex

exponential of the estimated phase.

With the same notations and calculus as in the

previous sub-section concerning FDD, we can derive the

measurements of phase and delay errors as follows:

()

),(

)()(

ˆ

)(2

)(

),()(

ˆ

)()()(

2

1

τϕη

ττα

τ

ϕ

η

ϕ

α

τ

ϕ

+

−

≅∆

+−≅∆

e

T

ss

OSF

s

ssss

(11)

These parameters are filtered by a second order filters

in order to estimate phase and delay. The structure of

these filters is the same as in FDD mode. But filters’

coefficients are different. This difference comes from the

difference in the gain, sampling frequency and updating

time period. We study in the following section these loop

filters.

3.5. Closed Loop Estimation

A Second-order loops should be able to track delay and

phase offset as long as the values of the coefficients is

carefully chosen.

So, the ∆τ can be filtered by a second order filter with

λ1 and λ2 as coefficients. The output of the filter is used

to determine the interpolator impulse response to find the

correct sample. In FDD mode the interpolator response is

updated every symbol (256 chips), but in TDD mode is

updated every slot (2560 chips). The interpolation filter

is updated for each symbol or slot (s) which is used to

correct the sampling instant error for the next symbol or

slot (s+1). Here we describe how a time loop filter

updates time delay:

)(

21

11

s

ss

kss

τ

λεε

λ

ε

µ

∆+=

∆

+

=

+

+ (12)

where µ is the estimated instant to be used by

interpolator and ε is the error of estimation.

With a similar structure the measurement ∆φ is

filtered by a second-order filter with two coefficients γ1

and γ2. The output of the filter is used to correct the

phase by complex multiplication. The phase is updated

every symbol in FDD mode and every slot in TDD mode.

So the calculated phase in symbol or slot (s) is used to

correct the phase of the next symbol or slot (s+1). The

following equation shows how a phase loop filter

updates the phase:

)(

21

11

s

ss

sss

ϕ

γδδ

γ

δ

φ

∆+=

∆

+

=

+

+ (13)

where φ is the estimated instant to be used by phase

corrector and δ is the estimation error.

From equations (10) and (12), we can derive the

expression of sampling instant estimation:

⎟

⎠

⎞

⎜

⎝

⎛+

−

+=

+)(

)(

ˆ

)(

)()(

1s

T

ss

sAzF

e

ss

η

ττ

αµµ

ττ

where Aτ depends on the mode (TDD or FDD):

and Fτ (z) is the loop filter transfer function:

1

2

11

)( −

−

+= z

z

zF

λ

τ

For the phase estimation, we find the same equation,

but filter coefficients are different:

⎟

⎠

⎞

⎜

⎝

⎛+

−

+=

+)(

)(

ˆ

)(

)()(

1s

T

ss

sAzF

e

ss

η

ϕϕ

αφφ

ϕϕ

again Aφ depends on the mode (TDD or FDD) :

NOVEL JOINT CHIP SAMPLING AND PHASE SYNCHRONIZATION 111

ALGORITHM FOR MULTISTANDARD UMTS SYSTEMS

and Fφ (z) is the loop filter transfer function:

1

2

11

)( −

−

+= z

z

zF

δ

ϕ

Estimator properties must be studied to determine

filter coefficients. We observe that the time loop filter

and phase loop filter have the same structure; in addition

they have the same structure for both of modes FDD and

TDD. So, we are studying the closed loop estimation in

the general case using this filter structure. In what

follows, we illustrate estimator properties in order to

demonstrate how filters’ coefficients are determined.

Figure 2 shows the diagram of a closed loop. We

denote by m the parameter that we want to estimate and

correct.

Figure 2. Estimation loop

The open loop transfer function of this system can be

written as:

)1()2(

)(

121

2

121

+−+−+

−

+

=

mmm

mAAzAz

AAzA

zH

where Am1 and Am2 are defined as :

2

11

β

mm

AA

=

2

We calculate the coefficients Am1 and Am2 for the case

of a stable system. In order to have two complex

conjugate poles, we should have

(

)

042

2

1<−mm AA , and

⎪

⎩

⎪

⎨

⎧

>

<

0

2

21

m

mm

A

AA (14)

If the first condition is verified then the poles of Hm(z)

are:

⎪

⎩

⎪

⎨

⎧

+−−−

=

+−+−

=

2

42

2

42

2

11

*

2

11

mmm

m

mmm

m

AAjA

p

AAjA

p

(15)

We have a second order system; this system can be

stable if the modules of its poles are smaller than one.

These conditions imply that

(

)

0442 122

2

1

2

1<−⇒<+−− mmmmm AAAAA

and with the first condition the criteria of stability

becomes:

⎪

⎩

⎪

⎨

⎧

<<

40

2

212

m

mmm

A

AAA (16)

In order to achieve good estimation, we must choose

filters’ coefficients which minimize the estimation error

(the residual error after convergence). With this criterion

we can calculate the appropriate coefficients. From the

structure of the closed loop estimation (Figure 4), the

variance of the estimation error can be calculated as

follows:

))(*)(

1

var()

ˆ

var( tth

A

mm m

η

=−

where hm(t) is the impulse response of the open loop

filter, and η(t) denotes an additive Gaussian noise. Let

)(*)()( ttht m

η

=

′

defines the filtered noise and N0 is the

power spectral density of the noise η(t). So the power

spectral density of the noise η’(t) is:

2

0)()(fj

mezH

A

N

f

π

η

==Γ ′

The variance of the noise η’(t) is relied to the power

spectral density by the following relation:

fdezH

A

N

fdft R

fj

m

R∫∫==Γ=

′′

2

0)()())((var

π

η

By proceeding to a variable change, the integral can

be calculated on the unit circle in Z plane.

dz

zpzp

zz

pzpz

zz

Aj

AN

mm

m

mm

mm ∫−−

−

−−

−

=)1()1(

1

)()(2

)(var**2

2

10

π

ε

(17)

where zm is the zero and pm is the pole the transfer

function. The function to be integrated have four poles,

112 Y. SERRESTOU ET AL.

two of them are out of the unit circle in Z plane, so by

using the residue theorem we can calculate this integral

then we obtain:

(

)

()

[

]

mmmm

mm

zpezp

pp

A

AN m)(411

)1(1

1

)(var 2

2

01ℜ−++

−−

=

ε

(18)

To find filters’ coefficients with efficient estimator,

the variance of the estimator must be optimized. There is

a region of coefficients that allows to an accepted

variance relative to Cramer-Rao bound. Also in

simulation we have found that for these values the

variance of estimation error is minimal. From these

values we can calculate the different filters’ coefficients.

In the FDD mode, and for the time loop filter (TLF)

we fix the coefficient as follows:

OS

F

A2

=

τ

,

CPICH

G

OSF•

=15.0

1

λ

and

CPICH

G

OSF

•

=05.0

2

λ

and for the phase loop filter (PLF):

CPICH

GA 2=

ϕ

,

CPICH

G

3.0

1=

δ

and

CPICH

G

1.0

2=

δ

If we don’t know the gain of the channel CPICH

(which is less than one) we fix it to one. Even for this

case we are sure that our system is stable and the

estimation error stay minimal.

In the TDD mode, for the time loop filter (TLF) we

fix the coefficients to the following values:

OSF

A2

=

τ

, OSF3.0

1=

λ

and OSF•= 1.0

2

λ

and for the phase loop filter (PLF):

1=

ϕ

A, 6.0

1=

δ

and 2.0

2=

δ

4. Simulation Platform

In order to test the proposed algorithm and to determine

all necessary parameters for implementation, we have

carried out an environment of simulation. The UMTS

base band signal in different modes is defined as well as

the propagation channel.

Figure 3 shows the modeling of the propagation

channel, that we consider in simulation context. For the

Fading phenomena we use a classic Jake’s spectrum

noised with a complex Gaussian noise to model the

Doppler’s effect and the frequency selectivity. The

Doppler frequency is considered as variable. The

simulated noise is an AWGN. The variance of this noise

determines the signal to noise ratio (SNR). In order to

introduce delay time in transmitted signal, the samples

are delayed by interpolation. We have simulated

different sampling drift functions; linear function and

triangular function. To shift the phase, the transmitted

signal was multiplied by complex exponential of a

variable phase. Many forms of shift functions are

experimented to evaluate the performance of our

algorithm.

Figure 3. Propagation channel modeling

We try here to show the performance of our algorithm.

So we show the obtained results for many configurations.

In the first configuration, we considered the FDD mode,

and three physical channels, i.e. three spreading codes, to

be transmitted. Two channels contained random data

and the third is the particular channel CPICH. The

spreading factors are SF1=SF2=16 and SF of CPICH is

256. To introduce time delay in the transmitted signal we

use a drift with 100 ppm (10-4 T

e of drift per sample

duration). And we shift the phase linearly by a

coefficient of 194 radian/s. and we fix Doppler

frequency to 220 Hz i.e. 120 km/h. and one propagation

path is considered. The SNR is variable. The following

Figures 4 and 5 show both real and imaginary parts of

the received CPICH channel for two values of SNR

(SNR=5 dB and 15 dB), where the transmitted symbol

value of this channel is (1+j). We obtain this figure by

correlation between the corrected received signals and

scrambling code as it described in the section “estimation

in FDD mode”. So these results show the stability,

convergence and efficiency of our algorithm.

10 frames are simulated, which correspond to 1500

symbols of CPICH channel. The real and imaginary parts

converge to 1. The transient phase takes about 10

symbols duration, so the convergence is established after

ten to fifteen symbols. That means the synchronization is

quickly established and maintained. We observe that the

variance of synchronized symbol depends on the SNR.

Figure 6 shows the constellation of CPICH for the

same values of SNR.

As it has described before our algorithm is based on

joint estimation of time delay and phase shift. So to

study our estimator we search for unbiased and optimal

estimators. For the first criteria we observe the

convergence of estimation and for the second we look to

minimize variance.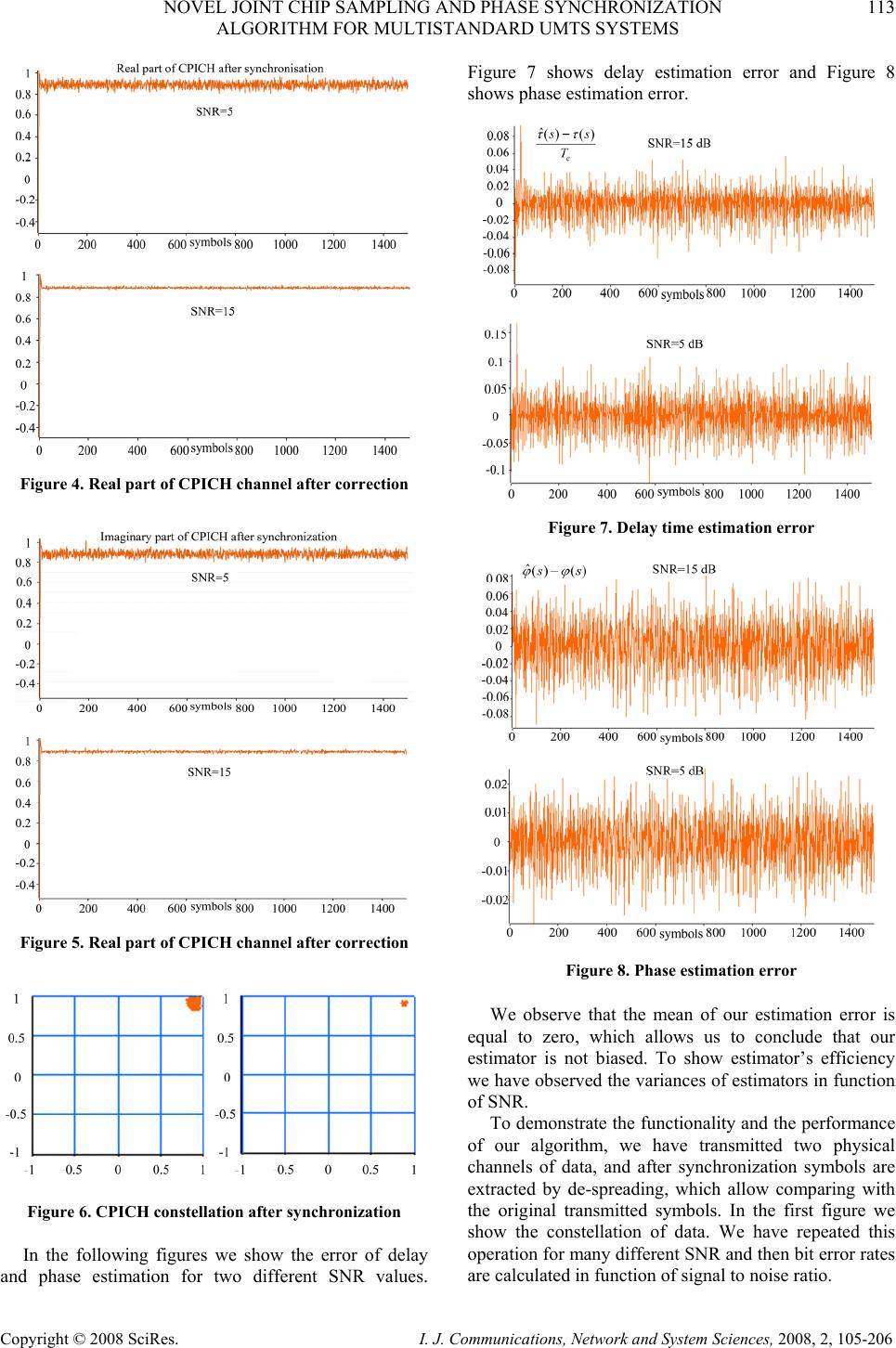

NOVEL JOINT CHIP SAMPLING AND PHASE SYNCHRONIZATION 113

ALGORITHM FOR MULTISTANDARD UMTS SYSTEMS

Figure 4. Real part of CPICH channel after correction

Figure 5. Real part of CPICH channel after correction

Figure 6. CPICH constellation after synchronization

In the following figures we show the error of delay

and phase estimation for two different SNR values.

Figure 7 shows delay estimation error and Figure 8

shows phase estimation error.

Figure 7. Delay time estimation error

Figure 8. Phase estimation error

We observe that the mean of our estimation error is

equal to zero, which allows us to conclude that our

estimator is not biased. To show estimator’s efficiency

we have observed the variances of estimators in function

of SNR.

To demonstrate the functionality and the performance

of our algorithm, we have transmitted two physical

channels of data, and after synchronization symbols are

extracted by de-spreading, which allow comparing with

the original transmitted symbols. In the first figure we

show the constellation of data. We have repeated this

operation for many different SNR and then bit error rates

are calculated in function of signal to noise ratio.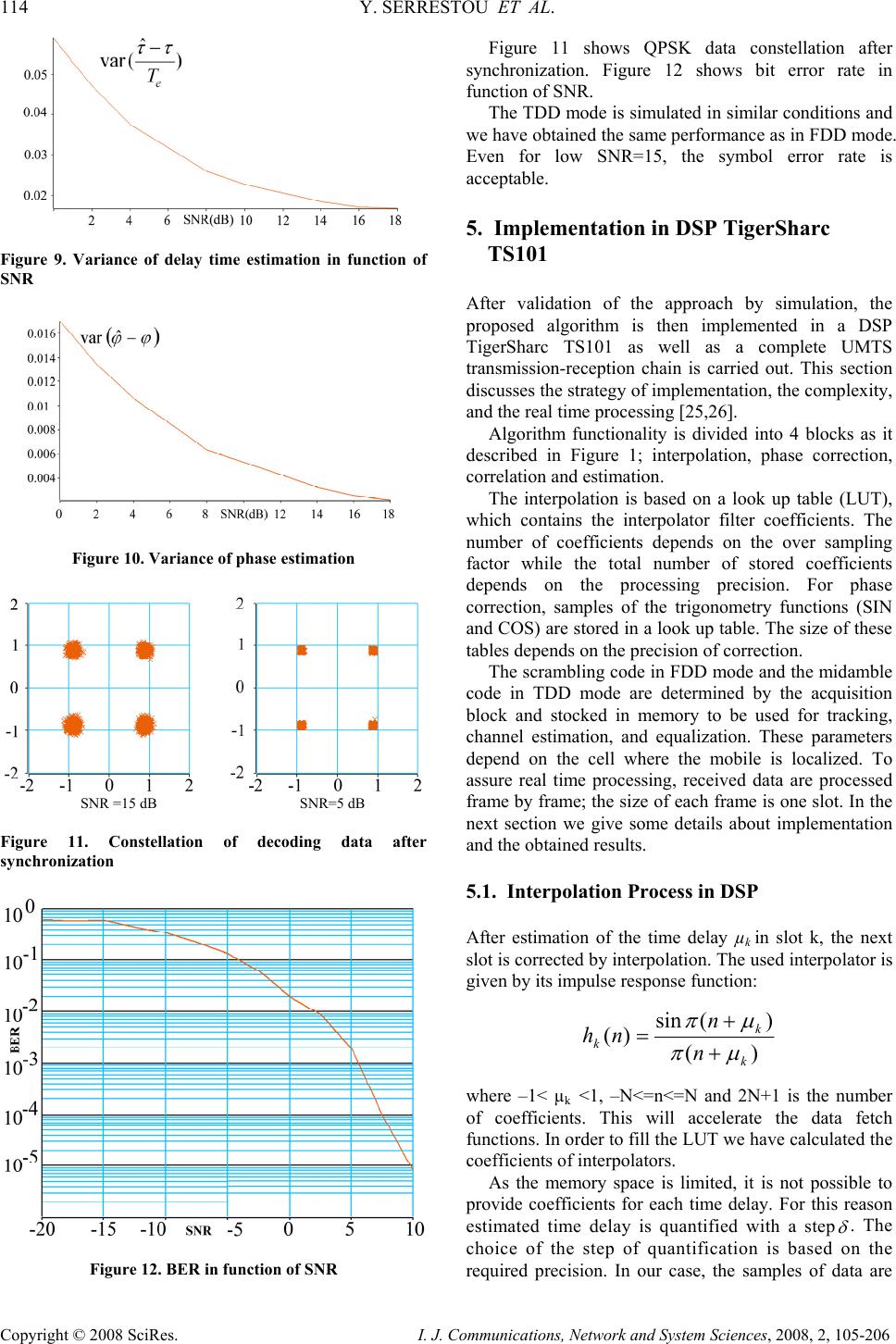

114 Y. SERRESTOU ET AL.

Figure 9. Variance of delay time estimation in function of

SNR

Figure 10. Variance of phase estimation

SNR =15 dB SNR=5 dB

Figure 11. Constellation of decoding data after

synchronization

Figure 12. BER in function of SNR

Figure 11 shows QPSK data constellation after

synchronization. Figure 12 shows bit error rate in

function of SNR.

The TDD mode is simulated in similar conditions and

we have obtained the same performance as in FDD mode.

Even for low SNR=15, the symbol error rate is

acceptable.

5. Implementation in DSP TigerSharc

TS101

After validation of the approach by simulation, the

proposed algorithm is then implemented in a DSP

TigerSharc TS101 as well as a complete UMTS

transmission-reception chain is carried out. This section

discusses the strategy of implementation, the complexity,

and the real time processing [25,26].

Algorithm functionality is divided into 4 blocks as it

described in Figure 1; interpolation, phase correction,

correlation and estimation.

The interpolation is based on a look up table (LUT),

which contains the interpolator filter coefficients. The

number of coefficients depends on the over sampling

factor while the total number of stored coefficients

depends on the processing precision. For phase

correction, samples of the trigonometry functions (SIN

and COS) are stored in a look up table. The size of these

tables depends on the precision of correction.

The scrambling code in FDD mode and the midamble

code in TDD mode are determined by the acquisition

block and stocked in memory to be used for tracking,

channel estimation, and equalization. These parameters

depend on the cell where the mobile is localized. To

assure real time processing, received data are processed

frame by frame; the size of each frame is one slot. In the

next section we give some details about implementation

and the obtained results.

5.1. Interpolation Process in DSP

After estimation of the time delay µk in slot k, the next

slot is corrected by interpolation. The used interpolator is

given by its impulse response function:

)(

)(sin

)(

k

kn

n

nh

µπ

µ

π

+

=

where –1< µk <1, –N<=n<=N and 2N+1 is the number

of coefficients. This will accelerate the data fetch

functions. In order to fill the LUT we have calculated the

coefficients of interpolators.

As the memory space is limited, it is not possible to

provide coefficients for each time delay. For this reason

estimated time delay is quantified with a step

δ

. The

choice of the step of quantification is based on the

required precision. In our case, the samples of data are

NOVEL JOINT CHIP SAMPLING AND PHASE SYNCHRONIZATION 115

ALGORITHM FOR MULTISTANDARD UMTS SYSTEMS

coded with 12 bits. So the step size must be more than

2-11. Let k

µ

denotes the quantification value of µk so we

have:

2

)1(,11,

δ

δµδµδµµ

+=⇒+<<∃−<<−∀ mmmmkkkk

Then the impulse response function of the

interpolator k can be written as:

)

2

(

)

2

(sin

)(

δ

δπ

δ

δπ

++

=

mn

nh k

The data are coded with fixed point with fractional

format (Q12: 12 bits are used). So it is not useful to

choose precision for quantification of time delay more

than the precision used in data, because the time delay is

estimated by correlation of this data. So that time delay

can be quantified with a step of δ = 10-7. The LUT for

interpolation is organized as described in Figure 13. The

size of this table is:

()

δ

2

12 +=NS

where 2N+1 is the number of interpolation coefficients,

this number depends on the oversampling factor (OSF).

For OSF=2 we need 5 coefficients to assure good

precision and for OSF=4 or 8 we use only 3 coefficients.

The number of coefficients corresponds to the number of

samples used to extract the correct sample.

Figure 13. Interpolation coefficients LUT

5.2. Phase Correction & Processing in DSP

To store samples of trigonometric functions, complex

number representation is used, and the phase is

quantified with a step of:

512

π

δ

=

The following table shows the arranged functions in

the DSP memory:

Figure 14. Trigonometric functions LUT

The size of this table is 1024 words of 16 bits. SIN

and COS tables are stored in the same 32-bit word,

where the SIN samples are stocked in the more signified

16-bit (MSB) and COS samples in the last significant 16-

bit (LSB). This method allows the DSP to fetch and

execute complex multiplication in one clock cycle. So

we get benefit from the wide memory DSP structure.

5.3. Complexity of Tracking Algorithm

We have evaluated the number of cycles required for

every function and the total number of cycles required

for tracking. The criterion is to assure real time. We start

by giving all parameters, so we process slot by slot. The

time duration of one slot is Tslot=666.667 µs. the DSP

clock period is Tcycle=4 ns. We detail here the required

number of cycles, which depends on the mode used

(TDD or FDD) and the over sampling factor. Table 1

shows that for all values of OSF and for both modes, the

processing in real time is assured. The functions that

need an important number of cycles are interpolation and

correlation.

5.4. Implementation Results

For the same simulation conditions, the algorithm is

evaluated in a real experimental platform. The obtained

results demonstrate the efficiency of the proposed

tracking algorithm. For a signal to noise ratio SNR=5dB

the symbol error rate is lower than 0.1%.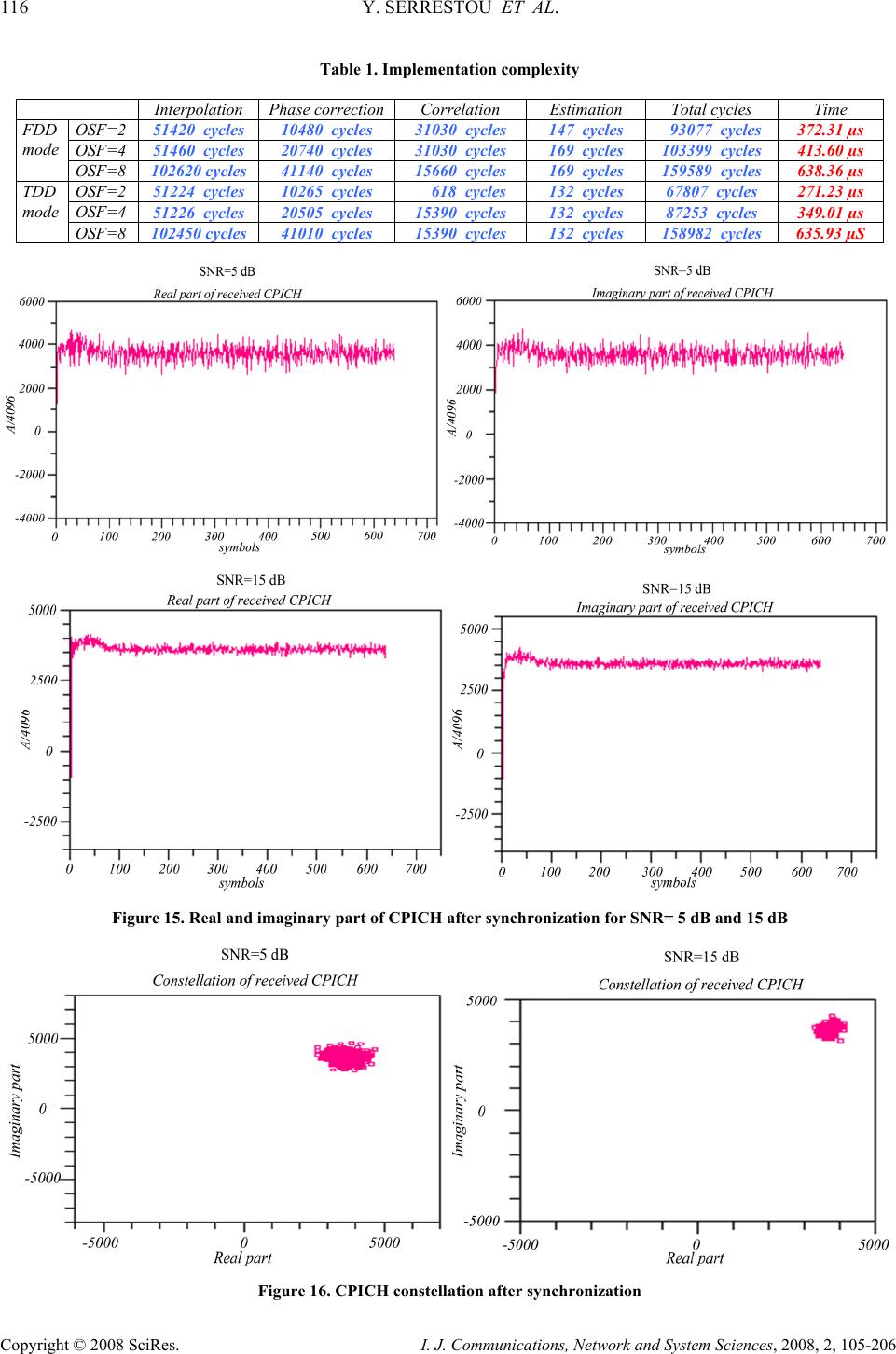

116 Y. SERRESTOU ET AL.

Table 1. Implementation complexity

Interpolation Phase correctionCorrelation Estimation Total cycles Time

OSF=2 51420 cycles 10480 cycles 31030 cycles 147 cycles 93077 cycles 372.31 µs

OSF=4 51460 cycles 20740 cycles 31030 cycles 169 cycles 103399 cycles 413.60 µs

FDD

mode

OSF=8 102620 cycles 41140 cycles 15660 cycles 169 cycles 159589 cycles 638.36 µs

OSF=2 51224 cycles 10265 cycles 618 cycles 132 cycles 67807 cycles 271.23 µs

OSF=4 51226 cycles 20505 cycles 15390 cycles 132 cycles 87253 cycles 349.01 µs

TDD

mode

OSF=8 102450 cycles 41010 cycles 15390 cycles 132 cycles 158982 cycles 635.93 µS

Figure 15. Real and imaginary part of CPICH after synchronization for SNR= 5 dB and 15 dB

Figure 16. CPICH constellation after synchronization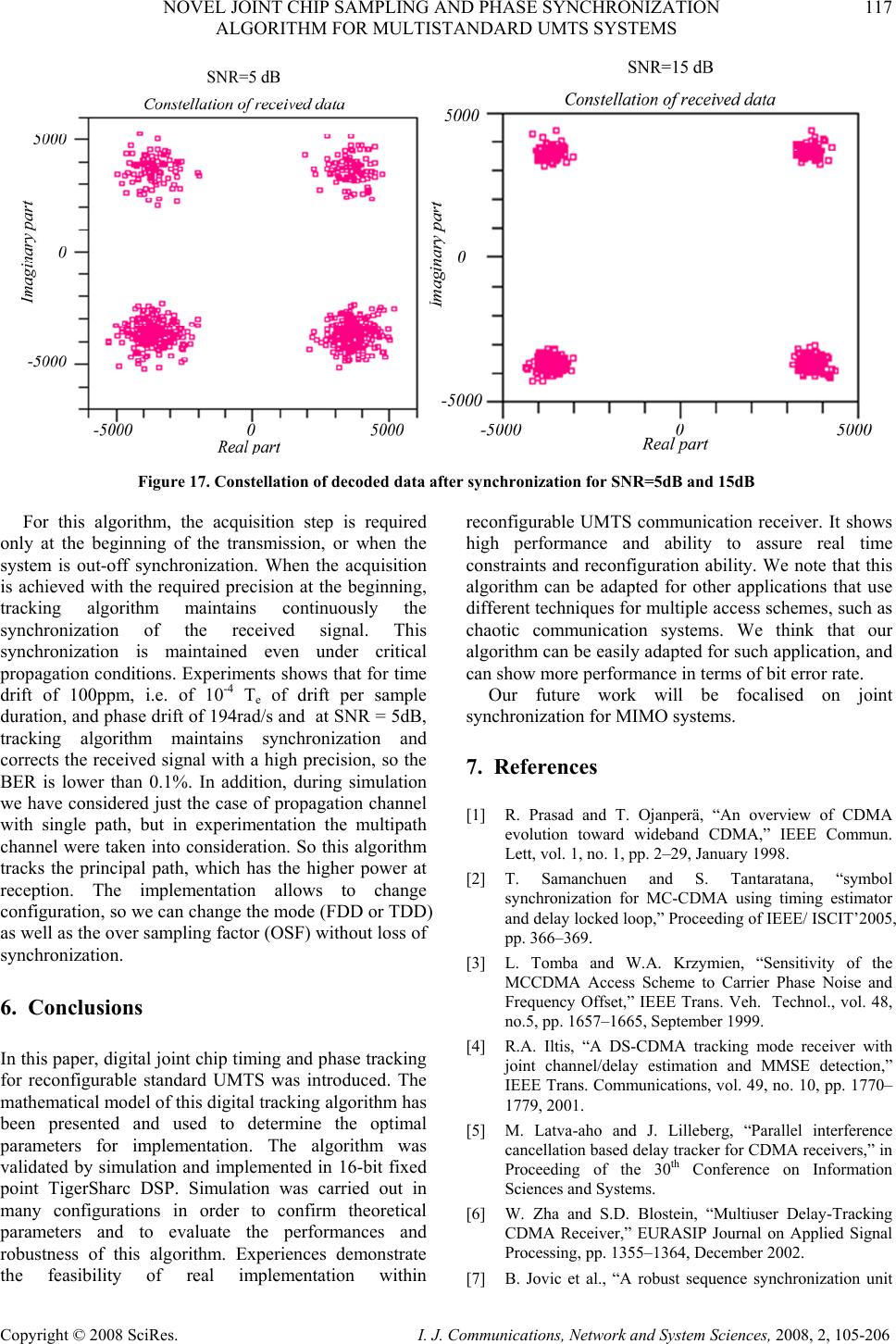

NOVEL JOINT CHIP SAMPLING AND PHASE SYNCHRONIZATION 117

ALGORITHM FOR MULTISTANDARD UMTS SYSTEMS

Figure 17. Constellation of decoded data after synchronization for SNR=5dB and 15dB

For this algorithm, the acquisition step is required

only at the beginning of the transmission, or when the

system is out-off synchronization. When the acquisition

is achieved with the required precision at the beginning,

tracking algorithm maintains continuously the

synchronization of the received signal. This

synchronization is maintained even under critical

propagation conditions. Experiments shows that for time

drift of 100ppm, i.e. of 10-4 T

e of drift per sample

duration, and phase drift of 194rad/s and at SNR = 5dB,

tracking algorithm maintains synchronization and

corrects the received signal with a high precision, so the

BER is lower than 0.1%. In addition, during simulation

we have considered just the case of propagation channel

with single path, but in experimentation the multipath

channel were taken into consideration. So this algorithm

tracks the principal path, which has the higher power at

reception. The implementation allows to change

configuration, so we can change the mode (FDD or TDD)

as well as the over sampling factor (OSF) without loss of

synchronization.

6. Conclusions

In this paper, digital joint chip timing and phase tracking

for reconfigurable standard UMTS was introduced. The

mathematical model of this digital tracking algorithm has

been presented and used to determine the optimal

parameters for implementation. The algorithm was

validated by simulation and implemented in 16-bit fixed

point TigerSharc DSP. Simulation was carried out in

many configurations in order to confirm theoretical

parameters and to evaluate the performances and

robustness of this algorithm. Experiences demonstrate

the feasibility of real implementation within

reconfigurable UMTS communication receiver. It shows

high performance and ability to assure real time

constraints and reconfiguration ability. We note that this

algorithm can be adapted for other applications that use

different techniques for multiple access schemes, such as

chaotic communication systems. We think that our

algorithm can be easily adapted for such application, and

can show more performance in terms of bit error rate.

Our future work will be focalised on joint

synchronization for MIMO systems.

7. References

[1] R. Prasad and T. Ojanperä, “An overview of CDMA

evolution toward wideband CDMA,” IEEE Commun.

Lett, vol. 1, no. 1, pp. 2–29, January 1998.

[2] T. Samanchuen and S. Tantaratana, “symbol

synchronization for MC-CDMA using timing estimator

and delay locked loop,” Proceeding of IEEE/ ISCIT’2005,

pp. 366–369.

[3] L. Tomba and W.A. Krzymien, “Sensitivity of the

MCCDMA Access Scheme to Carrier Phase Noise and

Frequency Offset,” IEEE Trans. Veh. Technol., vol. 48,

no.5, pp. 1657–1665, September 1999.

[4] R.A. Iltis, “A DS-CDMA tracking mode receiver with

joint channel/delay estimation and MMSE detection,”

IEEE Trans. Communications, vol. 49, no. 10, pp. 1770–

1779, 2001.

[5] M. Latva-aho and J. Lilleberg, “Parallel interference

cancellation based delay tracker for CDMA receivers,” in

Proceeding of the 30th Conference on Information

Sciences and Systems.

[6] W. Zha and S.D. Blostein, “Multiuser Delay-Tracking

CDMA Receiver,” EURASIP Journal on Applied Signal

Processing, pp. 1355–1364, December 2002.

[7] B. Jovic et al., “A robust sequence synchronization unit

118 Y. SERRESTOU ET AL.

for multi-user DS-CDMA chaos-based communication

systems,” in Signal Processing, vol. 87, pp. 1692–1708,

2007.

[8] R.L. Peterson, R.E. Ziemer, and D.E. Borth,

“Introduction to Spread Spectrum Communications,”

Prentice Hall, Inc., New Jersey, pp. 149–318 (Chapters 4

and 5), 1995.

[9] R.E. Ziemer and R.L. Peterson, “Introduction to Digital

Communication,” second edition, Prentice Hall, Inc.,

New Jersey, pp. 611–615 (Chapter 9), 2001.

[10] J.S. Lee and L.E. Miller, “CDMA Systems Engineering

Handbook,” Artech House Publishers, Boston, pp. 774–

837 (Chapter 7), 1998.

[11] S. Parkvall, E.G. Ström, and B. Ottersten, “The impact of

timing errors on the performance of linear DS-CDMA

receivers,” IEEE Journal on Selected Areas in

Communications, vol. 14, no. 8, pp. 1660–1668, 1996.

[12] J.C. Lin, “Low-complexity code tracking loop with chip-

level differential detection for DS/SS receivers,” IEEE

Electronic Letters, vol. 36, no. 24, 23rd November 2000.

[13] E. G. Strom, S. Parkvall, S. L. Miller, and B. Ottersten,

“Propagation delay estimation in asynchronous direct-

sequence code-division multiple access systems,” IEEE

Trans. Communications, vol. 44, no. 1, pp. 84–93, 1996.

[14] Y. Serrestou, K. Raoof, J. Liénard, “Digital joint

sampling instant and phase synchronization for UMTS

standard,” IEEE/ACES International Conference on

Wireless Communications and Applied Computational

Electromagnetics PN: 905565, Hawaii, 2005.

[15] F.M. Gardner, “Interpolation in digital Modems,” IEEE

Trans. on comm., vol.41, no.3, March 1999.

[16] 3GPP TS 25.211, “Physical layer-General description,”

Technical Specifications of the 3rd Generation

Partnership Project.

http://www.3gpp.org/ftp/Specs

[17] 3GPP TS 25.211, “Physical channels and mapping of

transport channels onto physical channel FDD,”

Technical Specifications of the 3rd Generation

Partnership Project.

http://www.3gpp.org/ftp/Specs

[18] 3GPP TS 25.212, “Multiplexing and channel coding

FDD,” Technical Specifications of the 3rd Generation

Partnership Project.

http://www.3gpp.org/ftp/Specs

[19] 3GPP TS 25.221, “Physical channels and mapping of

transport channels onto physical channel TDD,”

Technical Specifications of the 3rd Generation

Partnership Project.

http://www.3gpp.org/ftp/Specs

[20] 3GPP TS 25.222, “Multiplexing and channel coding

TDD,” Technical Specifications of the 3rd Generation

Partnership Project.

http://www.3gpp.org/ftp/Specs

[21] L. Krikidis, J.L. Danger, and L. Naviner, “A DS-CDMA

multi-stage inter-path interference canceller for high bit

rates,” 2004 IEEE Eighth International Symposium on

Spread Spectrum Techniques and Applications, pp. 405–

408, August 30 – September 2, 2004.

[22] L. Krikidis, J.L. Danger, and L. Naviner, “Flexible and

reconfigurable receiver architecture for WCDMA

systems with low spreading factors,” Electronics Letters,

vol. 41, no. 1, pp 22–24, January 6, 2005.

[23] F.M. Gardner, “Interpolation in digital Modems,” IEEE

Trans. on comm., vol. 41, no. 3, March 1999.

[24] R.E. Crochiere, “Optimum FIR digital filter

implementations for decimation, interpolation, and

narrow-band filtering,” IEEE Trans. on acoustics speech

and signal processing, vol. ASSP-23, no. 5, October 1975.

[25] A. Devices, “Tuning C source code for the TigerSharc

DSP compiler,” Engineer to engineer note, EE-147,

January 2001.

[26] A. Devices, “16-bit FIR filters ADSP-TS20x TigerSharc

processors,” Engineer to engineer note, EE-211, January

2004.

Paper Menu >>

Journal Menu >>