Paper Menu >>
Journal Menu >>
 Applied Mathematics, 2011, 2, 403-409 doi:10.4236/am.2011.24049 Published Online April 2011 (http://www.SciRP.org/journal/am) Copyright © 2011 SciRes. AM Stationary Characteristics of the Single-Server Queue System with Losses and Immediate Service Quality Control Aleksey I. Peschansky Sevastopol National Tech nical University, Sevastopol, Ukraine E-mail: peschansky_sntu@mail.ru Received December 27, 2010; revised January 31, 2011; accepted February 1, 2011 Abstract Semi-Markovian model of operation of a single-server queue system with losses and immediate service qual- ity control has been built. In case of unsatisfactory request service quality, its re-servicing is carried out. Re-servicing is executed till it is regarded satisfactory. Time between request income, and request service time are assumed to be random values with distribution functions of general kind. An explicit form of the system stationary characteristics has been defined. Keywords: Queue System, Semi-Markovian Process, System Stationary Characteristics, Request Service Quality 1. Introduction A large number of works [1-4] are dedicated to the queue systems with losses. In most of them the incoming flux of requests is supposed to be Poisson one or request ser- vice time is considered to have exponential distribution. This admission allows efficient modeling of the system operation by means of Markovian processes. But if the incoming flux of requests makes a renewal process and request service time distribution is of general kind, es- sential difficulties arise when defining system stationary characteristics in explicit form. To overcome them an apparatus of semi-Markovian processes with a common phase field of states is used in the works [5,6]. Thus, in [6] stationary characteristics of the single-server queue system 10GI G with losses were found. In the pre- sent article analogical characteristics for the same system have been defined under the assumption that the server admits both satisfactory and unsatisfactory request ser- vice. In case of the latter one the re-servicing begins im- mediately. It is repeated until the service is regarded sa- tisfactory. In the second chapter of the article the system opera- tion is described, mathematical problem definition and research purpose are stated. In the third section semi- Markovian model of system operation is built, and sta- tionary distribution of embedded Markovian chain is given. In the fourth section system stationary characteris- tics are defined. These are: final probabilities that the server is free, is in state of service or re-servicing, and mean dwelling times in these states. Besides, formulas of the system stationary characteristics for some subcases are given here. One of them is the exponential distribu- tion of time between request income and request service time. 2. The Problem Definition Let us investigate the queue system (QS) 10GIG with losses and a single server. Request service time is a ran- dom value (RV) with an absolutely continuous dis- tribution function (DF) F tP t and density f t. Time period between requests’ income is a RV with an absolutely continuous DF Gt Pt and density g t. If the server is busy with request ser- vice, all the incoming requests are lost. With the proba- bility p request service is regarded to be successful, and the queue system passes into a standby state that lasts till next request comes. With the probability 1qp the request service is considered unsatisfacto- ry, and the server begins re-servicing immediately. Time period of such a kind of service is a RV with an ab- solutely continuous DF tP t and density t . After re-servicing with the probability p the  A. I. PESCHANSKY Copyright © 2011 SciRes. AM 404 service is regarded satisfactory and with the probability q the request is sent to re-servicing procedure . This pro- cess lasts until the service is considered sufficient. It is assumed that RV , and are independent, have finite mathematical expectations ,, M MM and variances ,,DDD respectively. It is necessary to define the following stationary characteristics of the sys- tem: the final probabilities that the queue system is in a standby state; that the system is busy with the primary service or re-servicing; mean time periods of system’s dwelling in the above-mentioned states. 3. Semi-Markovian Model Building In order to build the model of the system operation an apparatus of semi-Markovian processes with a discrete- continuous phase field of states [6,7] is used. Let us de- scribe the system operation with the help of semi- Marko- vian process (SMP) t with a phase field 21,10,21,22,12Exxxx. Let us write out the codes of the states: 21 – service of the request that has come begins; 10x – request service has been successfully co mpleted, the server passes into a standby state that lasts time x (till the next request income); 21x – the incoming request has been lost, the server is busy with the primary service that will last time x; 22x – the incoming request has been lost, the server is busy with re-servicing that will last time x; 12x – request service has been completed, and its re- servicing has begun, time x is left till the next request income. In Figure 1 time diagram of the system operation is shown, and in Figure 2 there is the system transition graph. System dwelling times in the states are defined by the formulas: 211021 2212 ,, , xxx x x xx , where is a sign of minimum. Let us define the probabilities and probability densities of the embedded Markovian chain (EMC) ,0 nn transitions: 21 10 21 21 00 12 21 21 10 0 d, d, d, 1, xx xx pgtfxtt ppftgxtt pqftgxttP 21 10 21 21 12 21 ,; ; ; xx yy x y pgyxxyppgyx pqgyx 22 10 22 22 12 22 ,; ; ; xx yy x y pgyxxyppgyx pqgyx 10 22 12 12 12 12 ,; ; ,. xx yy x y ppyxxypyx pqyxxy Now we can proceed to EMC stationary distribution definition, the system of integral equations for its defini- tion is the following one: 21 0 21 0 21 0 21 21 0 2121dd , 2222d12d , 1212dd2122d , 1012dd2122d , 10d,10 xx x xx xx xgyx yygyxfyy x gyxyyyxyy x qyxy yqfyxgy yqgyxyyy x py xyypfy xgyypgyxyyy xx 0 122122d 1.xxxxx (1) Let us introduce the following integral operators: d, d,d, g f xxx A gyxyyAyx yyAfyx yy 000 d, d,d. g f A gyx yyAyx yyAfyx yy 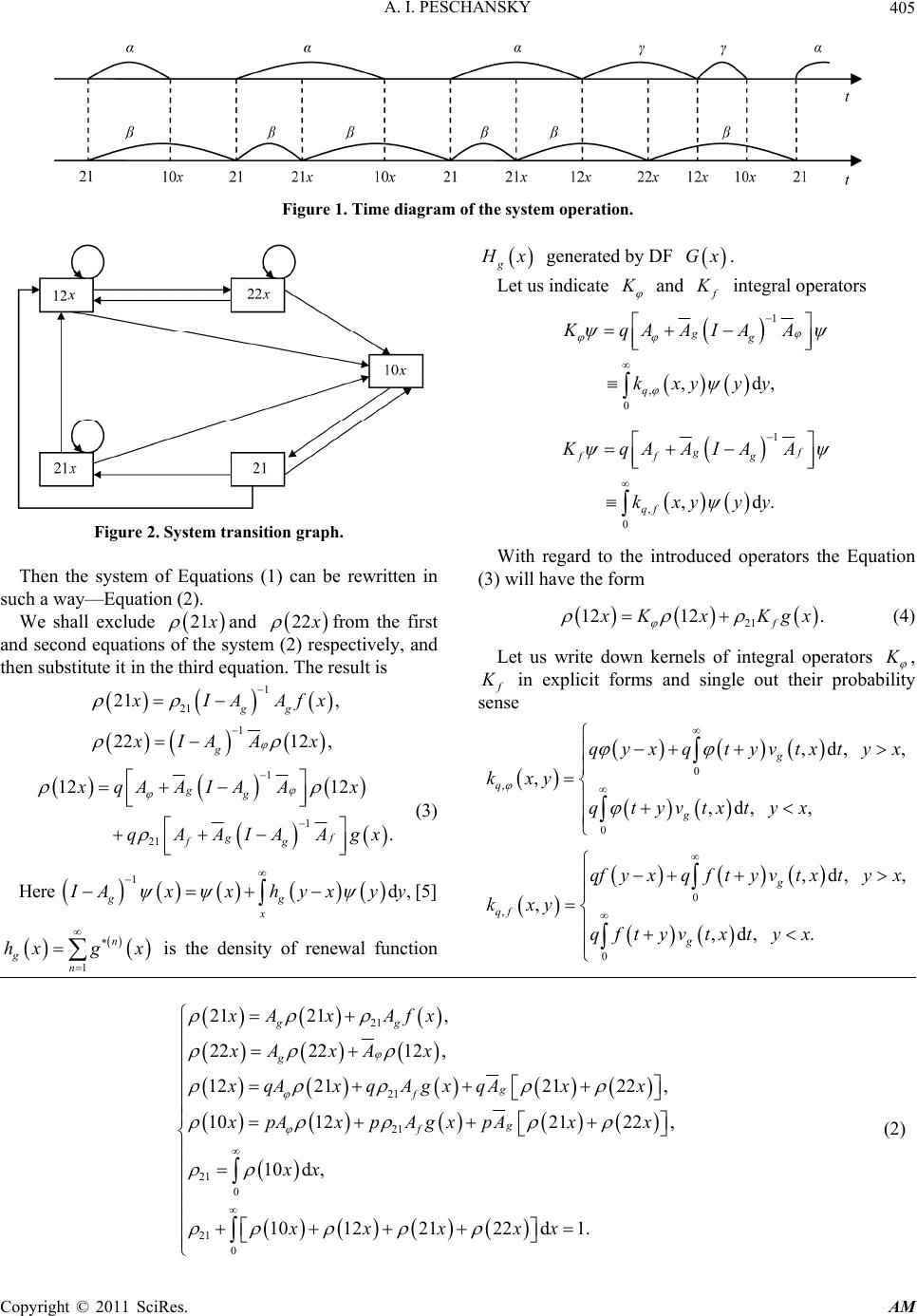 A. I. PESCHANSKY Copyright © 2011 SciRes. AM 405 Figure 1. Time diagram of the system operation. Figure 2. System transition graph. Then the system of Equations (1) can be rewritten in such a way—Equatio n ( 2). We shall exclude 21 x and 22 x from the first and second equations of the system (2) respectively, and then substitute it in the third equation. The result is 1 21 1 21 , 2212 , gg g x IA Afx xIAA x 1 1 21 12 12 . gg gf fg xqAAIA Ax qAAIAAgx (3) Here 1d, gg x I Axxhyxyy [5] 1 n gn hxgx is the density of renewal function g H x gene rat ed by DF Gx. Let us indicate K and f K integral operators 1 , 0 ,d, gg q KqAAIAA kxy yy 1 , 0 ,d. gf ff g qf KqAAIAA kxy yy With regard to the introduced operators the Equation (3) will have the form 21 12 12. f x KxKgx (4) Let us write down kernels of integral operators K , f K in explicit forms and single out their probability sense 0 , 0 ,d, , , ,d, , g q g qyxq tyvtxtyx kxy qtyvtxtyx 0 , 0 ,d, , , ,d, . g qf g qfyx qftyvtxtyx kxy qftyvtx tyx 21 21 21 21 0 21 0 21 21, 222212 , 12212122, 10122122, 10d, 10122122d 1. gg g g f g f xA xAfx xAxA x xqA xqAgxqAxx x pA xpAgxpAxx xx xxxxx (2)  A. I. PESCHANSKY Copyright © 2011 SciRes. AM 406 Here 0 ,d t gg v txgt xgt xuhu u is the density of the direct residual time t for the renewal process generated by RV 1 :ttt [8]. The func- tions ,, q kxy and , 0 ,d qf kxygyy are densities of probabilities of system transition from the state 12y to the nearest state 12x and from the state 21 to the nearest one 12x respectively. As , 0000 ,ddd,d 1, y qg kxyxq yxxqxtyvtxt qy yq it is not difficult to ensure that the operator K is the operator of contraction in the space of summable func- tions. That is why the solution of Equation (4) can be found by means of successive approximations. This solu- tion with regard to the identity 1 0 ,d ggg qAIAfxqvyxfyy can be represented in the form 21 1 12 , nn n x ql x (5) where 10 ,d g lxv yxfyy is the density of RV that is time period between the end of primary request service and the moment of the next request income. The function 1 0 ,d,2 n l ng lxvyx yyn is the den- sity of random time period between the end of the 1 s t n request re-servicing and the moment of the next request income. Here 11 10 ,d nn y ll gn g vyxlyxhyuguxu is the density of the direct residual time for the renewal process 1n l g H x generated by the functions 11 0 d x nn Lx ltt and Gx. Let us note that the density of renewal function complies with the ratio 111 0 d. n x l gnn g hxlxlxuhuu The rest of EMC stationary distributions are defined by the formulas 21 1 10 , nn n p x ql x q 21 21d , g x x hyxfyy 21 10 21 100 22 d dd. nn n nn n xqxylyy qy xyslss (6) The stationary probability 21 of EMC’s dwelling in the state 21 is found with the help of normalization re- quirement: 1 21 1 00 2d d. n l n gg n fxHxxqsHs s 4. Definition of System Stationary Characteristics Mean values of system dwelling times in the states are defined by the formulas 21 10 0 21 2212 00 d, , d, d. x xx xx x MFtGttMx M MGttM tt (7) Let us consider the following disjoint subsets of sys- tem states: 010Ex, 121,21Ex, 212, 22Exx. Dwelling in the state 0 E means that the server is free and the system is in a standby mode. Dwelling in the state 1 E or 2 E signifies that the server is busy with the primary request service or with re-ser- vicing respectively. Let us introduce SMP t transition probabilities: 012 ,,0 , . ii teEPt Ee eEEEE As it is known [9], under the condition of the unique EMC ,0 nn of SMP t stationary distribution existence the following ratios take place 1 lim,,dd, 0,2, i i tEE teEme eme ei (8) where me is mean SMP t dwelling time in the state eE . With the help of Formulas (5)-(7) integrals contained in the Formula (8) are converted into:  A. I. PESCHANSKY Copyright © 2011 SciRes. AM 407 1 21 2121 000 ddddd, x g E x meeFtGttxGtthyxfyy M 2 21 100 000 21 00 00 ddd dd dddd, xx nnn n E x gn meeqlxxt tdxxyl y yGt t q xGtthyyxy sl ssM p 0 21 10 21 1 00 dd 1dd , n nn n E l n gg n p meeqlxxx q q MftHttqtHttMM p 21 1 00 d1 dd. n l n gg n E meeMf tHttqtHtt Consequently, the final probability that the server is free is defined by the formula 00 1 00 lim,,1 1d d n tl n gg n q MM p pteE M ftH ttqtHtt (9) and the final probabilities p1 and p2 that the server is busy either with the primary service or with the re-servicing are: 11 1 00 lim,,, 1d d n tl n gg n M pteE M ftH t tqtHtt (10) 22 1 00 lim, ,. 1d d n tl n gg n qM p pteE M ftH ttqtHtt (11) It is necessary to note that the ratio 1 00 dd n l n gg n f tH ttqtHt t determines an average value of requests lost per time unit of a complete request service. Let us define mean stationary dwelling times i TE in the extracted subsets ,02 i Ei.. According to [7 ] we have 1 \ dd,,0.2 ii ii EEE TEme eePeEi . (12) One can define the values of expressions in denomi- nators of Formulas (12). To do it let us take integrals of both parts of the system (1) equations. The result is 0 021 \0000 21 21 0000 21 2 0 d,d21d12d 22d dd12d12d 12d EE ePeE pftGttpGxxxpxxxpGxxx pftGttpFxgxxpxxxpxxx pp xxp 12121 , q pp  A. I. PESCHANSKY Copyright © 2011 SciRes. AM 408 1 121 \0 d,10d, EE ePeEx x 2 22121 2121 \0000 d,d21ddd . EE ePeEq ftGttqGxxxq ftGttq ftGttq Consequently, mean system dwelling times in the extracted subsets are defined by the formulas 01 00 1d, n l n gg n q TEMftHtdtqtHt tMM p 12 1 ,.TE MTEM p (13) It is necessary to note that in case if with the probabil- ity equal to 1 satisfactory request service is carried out the system characteristics defined by the Formulas (9), (10) and (13) coincide with ones found in [6]. To illustrate some subcases of the results gained let us write down QS 10, 10,10MMMGGIM cha- racteristics. The system 10MM stationary characteristics. If the RV ,, densities have the form t f te , ,,0 tt gtete t sys tem stat ionary cha- racteristics are defined by the formulas 11 01 1 2 1,1, 1, qq pp pp pp pqq 012 11 1 ,, . TETETE p The system 10MG stationary characteristics. In case when ,0, t gte t and densities , f t t are of general kind we have , t n lx e , n l g H xx 1 00 1 dd . n l n gg n n n f tH ttqtHt t q MMqMM p The Formulas (9)-(11) and (13) for defining system stationary characteristics convert into 01 2 1,, 11 , 1 M pp qq MMMM pp qM p pq MM p 01 2 11 ,, .TETEMTEM p The system 10GI M stationary characteristics. For this system the incoming flux of requests is generated by RV with density g t of a general kind, and ,,0 tt ftete t . Let us find the func- tionals contained in the formulas for defining stationary characteristics. We have 00 0 dd d, 1 gg tg f tH ttFtht t g ehtt g where 0 d t g gtet is Laplace transformation of the density g t; 11 00 11 0 dd 1 d. 1 nn n ll nn gg nn l nt n gn nn qtHttq thtt qehttql g From the recurrence formula 1 0 1 00 d d,d nn ng ltsl sts luuvytyuy the recurrence formula for defining n l can be con- cluded: 11 000 11 dd,d d d1 ty t nnn g nn ltltetltvytey g ll g That is why the sum of series  A. I. PESCHANSKY Copyright © 2011 SciRes. AM 409 1 1 1 nn n Sql g is the solution of differential equation 1 1 ql SqS g . This solution obeys the condition 0 lim 1q gS p . This equation solution is defi- ned by the formula 11 0 d 1 p q qxlx Sx gx . As 11 gxg lx xg we find out that 1 0 d 11 p q qxgxg Sx gxgx . Consequently, system stationary characteristics are defined by the following ratios 0 1 0 11 1, 1d 1 p q q qg p p xgxg M x xgx 1 1 0 1, 1d 1 p q q g p xgxg M x xgx 2 1 0 1 , 1d 1 p q q qg p p xgxg M x xgx 12 11 ,,TETEp 1 00 11 d. 11 1 p q qxgxg q TE Mx gg p xgx 5. Conclusions In the present work semi-Markovian model of the opera- tion of the single-server queue system 10GI G with losses in which unsatisfactory request service quality is admitted has been built. Service quality control is carried out immediately, and in case of unsatisfactory service quality re-servicing is executed until the service is regar- ded as satisfactory. With the help of this model stationary characteristics in explicit form have been defined. These are: the final probabilities of system’s dwelling in a stan- dby state, in the states of primary service and re-servic- ing, and, besides, mean stationary dwelling times in these states. These characteristics depend on mean time period s between requests’ income, mean service time, average value of requests lost per time unit of a complete request service and the probability of unsatisfactory service. In case of satisfactory service only the ch aracteristics found coincide with the formerly defined ones. 6. References [1] J. Riordan, “Stochastic Service Systems,” Member Tech- nical Staff Bell Telephone Laboratories, Inc., John Wiley & Sons, Inc., New York, 1962. [2] B. V. Gnedenko and I. N. Kovalenko, “An Introduction to Queuing Theory,” Nauka, Moscow, 1987. [3] V. V. Anisimov, O. K. Zakusilov and V. S. Donchenko, “Elements of Queuing Theory and System Asymptotic Analysis,” Higher School, Kiev, 1987. [4] B. V. Gnedenko and D. Konig, “Handbuch der Bedie- nungsteorie II (For meen und Andere Ergebnisse),” Verlag, Berlin, 1984. [5] Y. Y. Obzherin and A. I. Peschansky, “Stationary Cha- racteristics of a Single-Server Queue System with a Sin- gle Waiting Space,” Cybernetics and System Analysis, Vol. 42, No. 5, 2006, pp. 51-62. [6] A. N. Korlat, V. N. Kuznetsov, M. I. Novikov and A. F. Turbin, “Semi-Markovian Models of Restorable and Ser- vice Systems,” Shtiintsa, Kishinev, 1991. [7] V. S. Korolyuk and A. F. Turbin, “Markovian Restoration Processes in the Problems of Sy stem Reliability,” Naukova Dumka, Kiev, 1982. [8] F. Beichelt and P Franken, “Zuverlässigkeit und Instan- phaltung. Mathematische Methoden,” VEB Verlag Technik, Berlin, 1983. [9] I. N. Kovalenko, N. Y. Kuznetsov and V. M. Shurenkov, “Stochastic Processes. Guidance,” Naukova Dumka, Kiev, 1983. |

