Journal of Power and Energy Engineering, 2014, 2, 198-202
Published Online April 2014 in SciRes. http://www.scirp.org/journal/jpee
http://dx.doi.org/10.4236/jpee.2014.24028
How to cite this paper: Dosaev, M.Z., Klimina, L.A., Lokshin, B.Ya., Selyutskiy, Y.D. and Hwang, S.-S. (2014) On Optimization
of Power Coefficient of HAWT. Journal of Power and Energy Engineering, 2, 198-202.
http://dx.doi.org/10.4236/jpee.2014.24028
On Optimization of Power Coefficient of
HAWT
Marat Z. Dosaev1, Lyubov A. Klimina1, Boris Ya. Lokshin1, Yury D. Selyutskiy1,
Shih-Shin Hwang2
1Institute of Mechanics, Lomonosov Moscow State University, Moscow, Russia
2Mechanical Engineering Department, Chien Hsin University of Science and Technologies, Zhongli City, Taiwan
Received December 2013
Abstract
The horizontal axis wind turbine (HAWT) blades rotation in the steady wind flow is considered.
We discuss the problem of determining the blade twist which could guarantee the maximum value
of the power coefficient. We define the blade twist as the technological turn of sections of blade
around its axis. This turn changes the effective pitch angle of turbine blade along its length. For
description of aerodynamic load upon the blades we used the quasi-steady approach. Air veloci-
ties of centers of pressure of blade sections are represented when taking into account components
induced by flow and vortex. We reduced the functional maximization problem to find the maxi-
mum of non-dimensional function. This function is given by Riemann integral depending on sec-
tion pitch angle and tip speed ratio. We suggested the algorithm for solving the problem under
consideration for a given blade shape.
Keywords
HAWT Blade; Tip Speed Ratio; Maximum of Power Coefficient
1. Introduction
The problem of designing the new shape for wind turbine blade is very complicated. Along with taking into ac-
count vibration and strength properties of blade, one must allow for necessity to utilize the maximum energy of
wind. Wide spreading of different types of wind turbine enables to construct engineering techniques for blade
design. For example, in [1,2] authors proposed the engineering method for choosing blades parameters, such as
the aerodynamic profile, blade width, pitch angle, and etc for several sections along the flow. On the other hand
the wind turbine aerodynamics is comprehensively studied [3]. Some authors use analytical approaches for
power efficiency estimating of wind turbine. The method based on using Goldstein functions is proposed in [4]
for ideal turbine with the finite number of blades. The simple enough algorithm of numerical estimation of the
upper bound of the power coefficient is suggested.
In present paper, we propose the analytical-computational approach for calculating the distribution of twist
blade angle along the blade length, which guarantee the maximum value of power coefficient for given blade
section profile and give distribution of blade width (Figure 1). We use the mechanical-mathematical model of

M. Z. Dosaev et al.
199
Figure 1. Blade twist for several sections.
aerodynamic load upon turbine blades developed in [5]. This model is based on quasi-steady approach. In order
to advance this model we introduce the components that related with induced velocities (see for example, [5]).
2. Problem Formulation
We consider the turbine with radius R (where R is a distance between axis of rotation and blade tip) that has n
blades (usually n = 3 - 6) and rotates with angular speed
Ω
in steady airflow. The wind speed W is directed
along the turbine axis. The output power P of turbine looks as following:
3
0.5( )
p
P CSW λρ = ⋅
,
where
λ
is TSR (tip speed ratio) of turbine,
ρ
is the air density,
2
SR π =
is turbine swept area,
()
p
C λ
is
the power coefficient that characterizes the efficiency of wind turbine.
We assume that the blade section, which is located at distance r (0 < r < R) from axis of rotation, represents
the given airfoil. The shape of section is the same for all blade sections. We formulate the following problem: to
determine the specified value
λ
and specified dependence
()r
ϑϑ
=
for twist angle of blade along its length,
which ensure the maximum value of power coefficient.
We use the flat cross-section hypothesis for needed characteristics obtaining. We allocate the section element
dr which is located at distance r from axis of rotation (Figure 2). Dependence b = b(r) is given. The air velocity
of point of intersection of blade axis and blade section is a sum of flow speed W(1 - а) and speed
(1 )ra
′
Ω+
of
its rotation. Here coefficients
,aa
′
to be determined are functions of r.
In Figure 3, the side view of this element is shown. In this projection, it is convenient to introduce all re-
quired values: pitch angle
θ
, angle of attack
α
, velocity
V
with respect to the flow, angle
φ
between the
turbine plane and
V
, and vectors
D
,
L
—components of the aerodynamic force (drag and lift, respectively)
acting upon the selected element. By construction, we have:
222 2
,tg(1) /(1)
(1)sin ,(1)cos ,
(1)() (1)
W ara
WaVra V
VWa ra
θ φαφ
φφ
′
=−= −Ω+
′
− =Ω+=
′
=− +Ω +
(2. 1)
Aerodynamic forces are defined by the following conventional formulae:
2
0.5( )
D
DCV dS αρ =
,
2
0.5( )
L
LCV dS αρ =
(2.2)
where
()dSb rdr=
is the element area, and aerodynamic coefficients
(), ()
DL
CC αα
are known functions for
a given airfoil [6]. Note that such approach to describing the aerodynamics was used in [7].
The aerodynamic torque
dM
with respect to the rotation axis produced on this element is given by the ex-
pression
(cossin )dMr LD φφ = −
or, taking into account (2.1) and (2.2),
()( )( ) ( )
()( )()()( )() ( )
2
2
2
2
0.5cos sin
0.51( )111
LD
LD
dMrb rCCV dr
rb rWa CaCrWaraWdr
αφα φρ
ρ αα
= −
′′
=−−+Ω× − +Ω+ 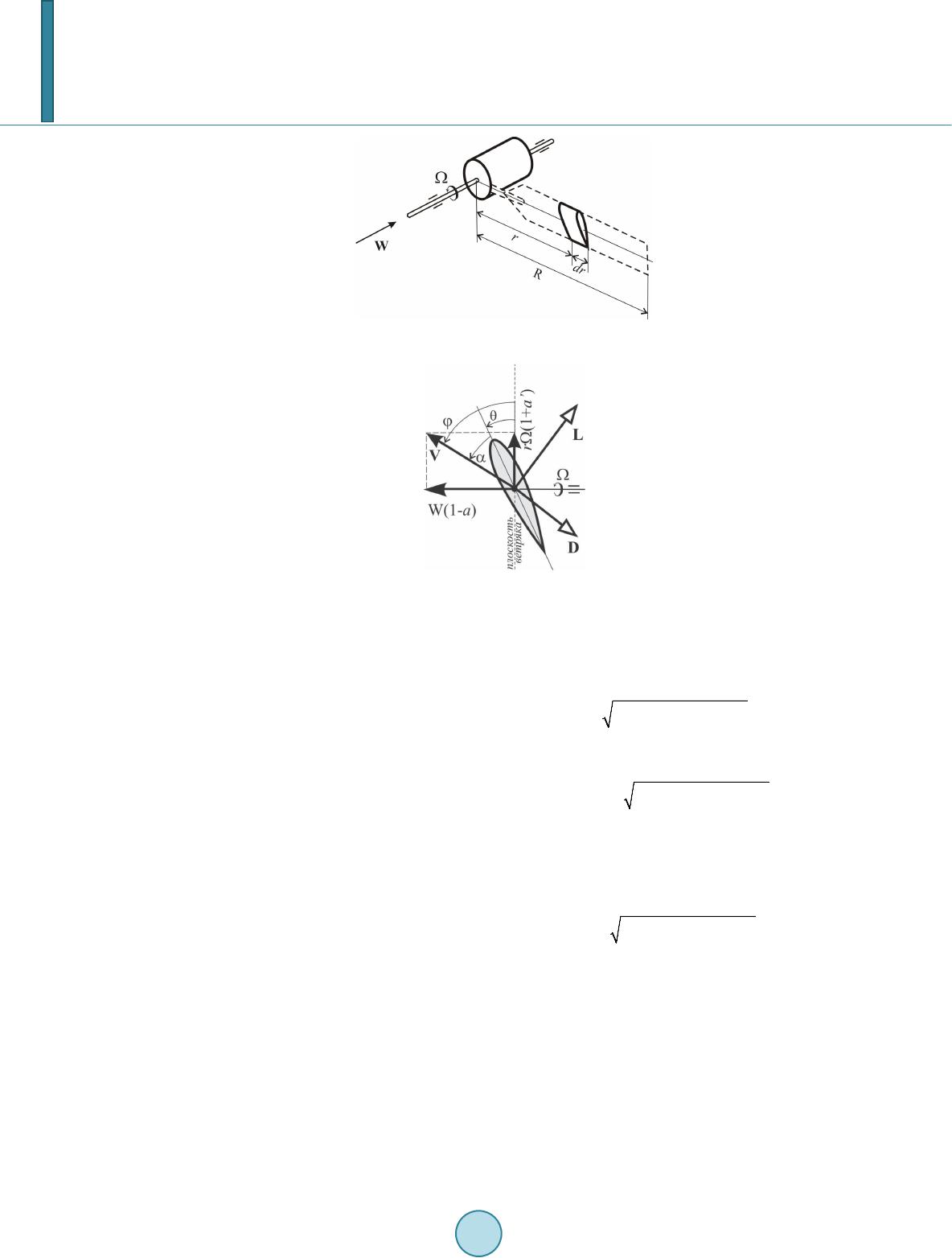


M. Z. Dosaev et al.
200
Figure 2. Blade element.
Figure 3. Side view of blade element.
Denote:
//r WrR ωλ =Ω=
(2.3)
Then the torque produced by all blades can be represented as an integral
()()() ()( )()()
22
22
0
0.5111 1
R
LD
MnWrb ra CaCaadr ρααωω ′′ =−−+− ++


∫
The power
PM= Ω
looks as follows:
()()( )()( )()()
22
31 2
0
0.5111 1
R
LD
PnWrb rRa CaCaadr ρ λααωω
−
′′
=−−+− ++


∫
(2.4)
Substituting r in (2.4) using the expression (2.3), we obtain
23
0.5( )Pn RW ρλ = Φ
(2 .5 )
Here the non-dimensional function is introduced
()()( )()( )()()
22
11 2
01 111
LD
bRa CaCaad
λ
λ λωααωωω
−− ′′
Φ=−−+− ++

 ∫
(2 .6 )
Comparing (2.5) with the general formula
23
0.5 p PC RW ρπ =
for the power produced by the wind turbine,
one can readily see that the following relation holds:
1
() ()
p
Cn λπλ
−
= Φ
, (2.7)
and the initial optimization problem is reduced to the problem of maximum search for the function (2.6).
3. Solution of the Problem
Before solving the problem of optimization of this coefficient (values to be varied are
()r θ
and
λ
, blade
chord b is a given function of
/rR ωλ =
, values
,aa
′
are also to be defined as functions of
/rR ωλ =
),
consider the process of calculation of the integrand in (2.6) for fixed
, ,,,rb ωλ θ
. For that, following [3], we

M. Z. Dosaev et al.
201
introduce the adjustment coefficient
2arccos() /
f
Fe π
−
=
, taking into account losses at the blade tip, where
( )/2fn λω ω = −
,
( )
1
2nb R σλπω
−
=
,
()cos ()sin
NL D
CC C αφαφ = +
is the component of aerodynamic
force along HAWT the axis, and
()sin ()cos
TL D
CC C αφ αφ = −
is the component of aerodynamic force lying
in the turbine plane. Then induced speeds coefficients can be represented as follows [3]:
( )
21
1
( )(4sin( )) ,
()4sin cos()
NN
TT
aC FC
aC FC
σα ϕσα
σα ϕϕσα
−
−
= +
′= −
(3.1)
Angles
α
and
ϕ
can be expressed as follows (using (2.1) and (2.3)):
α ϕθ = −
,
( )
( )
( )
11
arctg 11aa ϕω
−−
′ =−+
(3.2)
Relations (3.1)-(3.2) make a system of four equations with respect to
,,,aa ϕα
′
. Contrarily to the iterative
method of solving these equations proposed in [3,5], consider another way for determining the sought values.
Substituting (3.1) into the second Equation (3.2), we obtain
( )
( )
2
4sinsin cos0
NT
F CC ωϕϕϕ σω
−++=
(3.3 )
From here,
ϕ
is expressed via
,, αωλ
. In particular, for
0( )F ωλ ≈≈
we have:
[ ]
arctg() / ()
LD DL
CC CC ϕλλ =−−+
. After having solved (3.3), parameters
,aa
′
are also expressed from
(3.1) via
,, αωλ
, and then the angle
θ
is determined from the first Equation (3.2) as a function of the same
parameters
,, αωλ
. Thus, the integrand in (2.6) represents an explicit function of
,, αωλ
. Such representa-
tion is more preferable for solving the original problem of maximization of the coefficient
p
C
.
Now return to the problem of maximization of
p
C
, or of function
() λ Φ
. Taking into account that
λ
is a
constant (though unknown), the integral (2.6) can be interpreted as a functional defined on the class of differen-
tiable functions
()
αω
. Then the source problem is deduced to the problem of choice of a function
0
(,) αα ωλ =
that delivers maximum to the integral, and of subsequent choice of such a value
0
λ
that deliv-
ers maximum value to the function
()
λ Φ
.
In order to find
0
() αω
, we use the convenient method for solving variational problems, we obtain the fol-
lowing necessary condition of the maximum of the integral (Euler-Lagrange equation): the full derivative of the
integrand with respect to
α
is zero (this equation is not written here due to its complexity).
In [5], results of numerical solution of Equations (3.1)-(3.2) are given for several NACA airfoils, from which
one can see that coefficients
,
aa
′
almost do not change for
1 ω >
. Hence, we assume (as the first approxima-
tion) that
const, const
aa
′
= =
(3 .4 )
Then the mentioned Euler-Lagrange equation looks as follows
(1 )(1)0
LD
a dCdadCd αω α
′
− −+=
(3.5 )
From (3.5) it is possible to find
α
as a function of
ω
:
() α αω =
. One of branches of this solution will
contain the optimal dependence
0
(,) αα ωλ =
, and from (3.3) (or from (3.2)) it is possible to determine the in-
termediate variable
ϕ
, and then from (3.2) it is possible to derive the expression for the desired blade twist
containing the undetermined (so far) parameter
λ
:
()
( )
( )
011 0
( ,)arctg11( , )aa θ ωλωα ωλ
−−
′
= −+−
(3.6)
Substituting the obtained expression for
0
() αω
into the integrand in (2.6), we obtain the function
() λ Φ
of
single argument
λ
, maximum value of which is determined analytically (if possible) or numerically. Thus, the
desired optimal value
0
λ
will be found, after which the optimal blade twist is determined from (3.6) as a func-
tion of
0
, ((0,]) ωω λ ∈
. Note that
0
/, ((0,])rR rR ωλ = ∈
.
In principle, the problem is solved.
Taking into account dependences
(), ()
LD
CC αα
(e.g., [6]), one can show that the solution
() α αω =
of
Equation (3.5) exists as a monotonically decaying function. If it delivers maximum to the functional (3.6), then
upon having determined the optimal value of
0
λ
and returning back to the variable r, the optimal blade twist
can also be decreasing function
( )
( )()
( )
1
0 000
( )arctg11(/)rR raarR θ λαλ
−
′
=−+ −
.

M. Z. Dosaev et al.
202
This monotony is qualitatively confirmed by the practice of HAWT design.
4. Conclusion
In this paper we studied the problem of maximization of power coefficient for a HAWT by optimization of a
blade twist and tip speed ratio. We obtained an algorithm for determining of the optimal solution of this problem
in the frame of the quasi-steady model of aerodynamic action taking into account induced velocities. Each step
of this algorithm depends on parameters of the model, so the final shape of the twist can be specified for each
particular airfoil. Still qualitative features of the optimal solution remain for the general case: for instance, there
exists the optimal pitch angle function that is monotone along the blade length.
Acknowledgements
The work is partially supported by RFBR, projects NN 11-08-92005, 12-01-00364, and 14-08-01130.
References
[1] Perli, S.B. (1938) Windpump and Windelectrical Units. ONTI, Kharkov. (in Russian)
[2] Sabinin, G.H. (1931) Theory and Aerodynamic Calculation of Wind Engines. Trudi TsAGI, Moscow. (in Russian)
[3] Hansen, M.O.L. (2000) Aerodynamics of Wind Turbines. James and James, London.
[4] Okulov, V.L. and Sorensen, G. N. (2008) Ideal Wind Turbine with Finite Number of Blades. DAN, 420, 478-483. (in
Russian)
[5] Tenguria, N., Mittal, N.D. and Ahmed, S. (2011) Evaluation of Performance of Horizontal Axis Wind Turbine Blades
Based on Optimal Rotor Theory. Journal of Urban and Environmental Engineering, 5, 15-23.
http://dx.doi.org/10.4090/juee.2011.v5n1.015023
[6] Kashafutdinov, S.T. and Lushin, V.N. (1994) Atlas of Aerodyna mic Characteristics of Wing Airfoils. SO RASHN,
Novosibirsk. (in Russian)
[7] Dosaev, M.Z., Kobrin, A .I. , Lokshin, B.Ya., Samsonov, V.A. and Sely utsk iy, Yu.D. (2007) Constructive Theory of
Small-Scale Power Generators. Part I, MSU Publishing, Moscow.