 Journal of Power and Energy Engineering, 2014, 2, 169-175 Published Online April 2014 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2014.24024 How to cite this paper: Mao, Y.S., Tian, J.F. and Zhai, Q.Z. (2014) Wind Power Bidding Strategy Based on the Minimax Regret Criterion with Limited Distribution Information. Journal of Power and Energy Engineering, 2, 169-175. http://dx.doi.org/10.4236/jpee.2014.24024 Wind Power Bidding Strategy Based on the Minimax Regret Criterion with Limited Distribution Information* Yashan Mao, Jianfang Tian, Qiaozhu Zhai Systems Engineering Institute, MOE KLINNS Lab, Xi’an Jiaotong University, Xi’an, China Email: ysmao@sei.xjtu. edu.cn, j ftian@sei.xjtu.ed u.cn, qzzhai@sei.xjtu .edu.cn Received December 2013 Abstract In optimal wind bidding strategy related literatures, it is usually assumed that the full distribution information (for example, the cumulative distribution function or the probability density function) of wind power output is known. In real world applications, however, only very limited distribution information can be obtained. Therefore, the “optimal bidding strategy” obtained based on the hy- pothetical distribution may be far away from the true optimal one. In this paper, an optimal bid- ding strategy is obtained based on the minimax regret criterion. The salient feature of the new approach is that it requires only partial information of wind power distribution, for example, the expectation and the support set. Numerical test is then performed and the results suggest that the method established in this paper is effective. Keywords Bidding Strategy; Expected Profit; Partial Distribution Information; Minimax Regret Criterion; Imbalance Cost 1. Introduction Regarded as one of the most promising renewable resources, wind power is gaining importance in the power networks, and the proportion of wind power is also steadily increasing in the electricity markets in recent years. However, due to the intermittency and unpredictability of wind power generation, the realistic wind power deli- very amount is usually not equal to the bidding results determined in the day-ahead market. The wind power producer must pay the so called imbalance costs. Therefore, wind power producers are willing to adopt the op- timal bidding strategies which take two factors into consideration, i.e., both profit and imbalance cost. As a re- sult, wind power producers are striving to achieve maximum expected profit in day-ahead market. Although by using the wind power forecast results, wind producers can reduce the imbalance costs to some extent, high vola- tility of wind power makes the accuracy of long-term and even short-term forecast is much lower than that of the *The research was supported in part by the National Natural Science Foundation (61174146, 61221063), the Foundation for Authors of N a- tional Outstanding Doctoral Dissertation (201047).  Y. S. Mao et al. traditional load forecast, especially when the forecast horizon is extended [1,2]. Many approaches on optimal wind bidding strategies have been published in recent years. An optimal wind bidding strategy problem involving the existence of imbalance penalty and allowed imbalance band is consi- dered in [3], with analytical solutions provided under normal and Rayleigh distribution of wind power. A Cour- not model is employed in [4] to study the bidding strategies where the forecasting error is assumed to follow the normal distribution and the effects of forecasting error on the bidding results are also discussed in [5]. In [6-7], the realistic power outputs of the wind farm and the spot market prices are considered as independent random variables with known probability density functions to maximize the market participant revenue. It is found that the optimal bidding problems considered in the aforementioned approaches are all assumed to have full know- ledge of the wind power probability distribution, and the problem formulations are essentially equivalent to the well-known newsvendor problem [8]. However, in practice, since the randomness and volatility of the wind power generation in real-time, it is often difficult to accurately characterize the wind power distribution, espe- cially with little historical data or when different forecasts methods are used. On the other hand, it is much easier to obtain partial information of wind power distribution such as the range of wind power output (the support of the related random variable). Although the optimal wind bidding problems under the circumstance of lacking of distribution information of wind power are not fully discussed in literature, many different approaches [9-12], such as the maximin criterion, the minimax regret criterion and entropy maximization have been applied to the distribution-free newsvendor problem. Based on the mathematical equivalence of the two problems, some methods for solving the newsven- dor problem may be suitable for the wind bidding problems. The minimax regret criterion is thus adopted in this paper to find an optimal and robust bidding strategy. The only distribution information required by the method is the expectation and support of the wind power output. The contents of the paper are as follows. Section 2 provides an optimal bidding problem considering imbal- ance price mechanism and formulates it as a maximum expected profit model. An optimal bidding strategy based on the minimax regret criterion with partial distribution information of wind power is discussed in Section 3. The effectiveness and robustness of using this strategy are discussed based on a case study with the hypothe- sis that the wind power actually follows two commonly used distributions, and the results are stated in Section 4. The conclusion is then given in Section 5. 2. Problem Formulation In this paper, we follow the imbalance price mechanism model of the Nordic power market as described in [13]. The spot price, the imbalance price for overproduction (positive imbalance) and underproduction (negative im- balance) are all settled hourly, which can be derived from historical data. Although different imbalance price models depend on different market regulation rules, there exists a reasonable relation among the price for over- production ( ), the price for underproduction ( ), and the spot price ( ). It can be expressed by the fol- lowing inequality. (1) 2.1. A Basic Formulation The optimal bidding problem is to maximize the expected profit for the wind power producer trading in the day-ahead market. The complete day-ahead bidding scheme can be solved individually with 24-hour forecast data, and as a consequence, the bidding problem can be formulated hourly and expressed as follows, (){ }{ } max max,0max,0 t s sellbuy ttt tttttt p Rppwpp w λλ λ =+−− − (2) subject to (3) where pt is the quantity that the wind power producer bids in the day-ahead market for period t, represents the actual generation over the same time period, and is the upper bound of the wind power output (may be less than the installed capacity of the wind farm). However, the problem aforementioned cannot be solved directly since it includes a random variable  Y. S. Mao et al. which cannot be obtained in day-ahead. Thus, it’s necessary to change it into a deterministic one. 2.2. Maximum Expected Profit Model To deal with random variable in the basic formulation, a possible way is to use its expected value instead, which can be derived from a certain prediction model. Let represent the forecasting value. In addition, although inessential, we assume as a continuous random variable with a cumulative distribution function (c.d.f.) and the support of is an interval (i.e., and ). Then can be obtained as follows, (4 ) According to the above description (Equations (2)-(4)), is actually a function of random variable as stated in Equation (2), and the expected profit can be expressed as the following equation. (){ }{ } ()( )()( ) max ,0max ,0 tt tt s sellbuy ttt tttttt wp s sellbuy ttttttt ttt pw ERppEwpEp w pwpdF wpwdF w λλ λ λλ λ =+−− − =+− −− ∫∫ (5) So far, the original bidding problem has changed into a deterministic problem when and other para- meters are given. To maximize the expected profit of the wind producer, the expected value model can be estab- lished as follows, (6) subject to constraint (3). When , the objective function in Equation (6) turns into ( ) [ ] s sellsell t tttt p Ew λλ λ −+ , and therefore the optimal solution of Equation (6) is attained at since (see (1)). When , the function in Equation (6) is equal to ( ) [ ] s buybuy t tttt p Ew λλ λ −+ and therefore the optimal solution of (6) is attained at . Since the objective function in Equation (6) is continuous with varying from 0 to , the constraint (3) can thus be simplified as . For convenience, let buy s tt tbuy sell tt λλ βλλ − =− , and normalize the prices. By a simple algebraic transformation, the maximum expected profit model can then be finally rewritten as follows. ( ){} [ ] maxmin , sell t tt tttt buy sell tt ERp EpwpEw λ βλλ = −+ − (7) subject to (8) Note that this is a concave maximization problem, and solution which satisfies constraint (8) will be the glob- al optimal value. Additionally, if the wind power producer obtains the full knowledge of the possibilities of wind power distri- bution, the problem formulated can be regarded as the newsvendor model with the optimal bidding quantity eas- ily solved from the equation [8]. However, since the randomness and volatility of the wind power generation in real-time, the actual distribu- tion of the wind power is not necessarily known. On the other hand, it is much easier to estimate the expectation and the support of based on historical data. Thus, the urgent task is to propose a stochastically robust me- thod solving the optimal bidding problem with such limited distribution information of wind power. 3. Optimal Bidding Strategy Based on the Minimax Regret Criterion with Limited Information of Wind Power Distribution In what follows, the minimax regret criterion is adopted to solve the optimal bidding problem under uncertainty  Y. S. Mao et al. of wind power distribution. Supposing only the expectation and range of wind power output can be obtained, an optimal bidding strategy is then derived and proved in this section. 3.1. Optimal Bidding Problem with the Minimax Regret Criterion In absence of some information on the exact wind power distribution, the bidding quantity in the day-ahead market is usually regarded as unable to determine. Aiming at solving problem under this situation, we propose a methodology on the basis of the minimax regret criterion. As described in [12], the core idea of the minimax regret criterion is to minimize the wind power producer’s maximum profit loss from not making the optimal decision. Using this approach, problem in Equation (7) and (8) with this criterion can be reformulated as follows, ( )( ) { } ( ) ( )() { } { } ( { { } ) ( )() } minminmax max minmax max minmaxmaxmin ,min , tttttt ttt ttt ttt t t ttt ttt t ttt wpw wpwFwpw tt wpw wpwF w tttttt tt w wpw wpw F pERp ERp ERp ERp wpwp dFwpp θθ β ∗ ≤≤≤≤ ∈Ω≤ ≤ ≤≤ ≤ ≤∈Ω ≤≤ ≤ ≤∈Ω = =− = − =− +− ∫ (9) where ( ) { } ( ) max ttt tt wpw ERp ERp ≤≤ − measures the additional profit that could have been obtained with full information about the wind power distribution when given a decision and a probability distribution . is considered as the convex set of all possible distributions with the known support , and the maximum regret ( ) { } ( ) max max ttt tt F wpw ERp ERp ∈Ω≤ ≤ − can be regarded as the maximum possible loss in profit of the wind power producer when the exact wind power distribution is unknown. Additionally, the target of the inner problem ( )( ) { } max tt F ERp ERp ∈Ω − in Equation (9) is to find the distribution that maximized the regret for given and . 3.2. Optimal Bidding Strategy Based on the Minimax Regret Criterion with Expectation and Support Suppose the only information of the wind power distribution that can be obtained is the expectation and the support, based on the minimax regret criterion under this condition, [12] provides an optimal bidding strategy which can be adopted directly to solve the problem presented in this paper, and the optimal bidding strategy can be described as follows. If the distribution of wind power is nonnegative, with support and expectation , the optimal bid- ding quantity under the minimax regret criterion is equal to ( ) ( ) 2 1 1, 2 11 , 422 1 , 2 ttt tt tt tt tt t t tt tt tt tt t tt tt w if ww pwif ww ww w w if w ww β βµβ µµ β β µ ββ µ ∗ +− ≤ −− = +≤≤ − −− −≤ −− (10 ) It is necessary to emphasize that according to the derivation of this strategy presented in [12], the problem in (9), expressed as ( )( ) { } max tt FERp ERp ∈Ω − with wind power varying from to as well as the ex- pectation predicted in the period , can be formulated as follows, { }() ( ) () maxmin ,min , t t w tttt t w F wpwp dFw ∈Ω − ∫ (11 ) subject to  Y. S. Mao et al. (12) and (1 3) By strong duality [14], this problem is equivalent to the following dual problem (14) subject to { }{ } ( ) 01 min,min,0, ttttttt t wwpwpwww αα +−−≥∀≤ ≤ (15) which is a linear optimization problem, explicitly. Then, the optimal bidding strategy proposed in (10) can be easily obtained by solving this dual problem with detailed derivation presented in [12]. 4. Case Study The optimal bidding strategy proposed in Section 3 shows a straightforward result of bidding problem with par- tial information of wind power distribution. In this section, we first provide the illustrative results for a complete day-ahead bidding scheme based on the minimax regret criterion and then compare the profit from our approach with that based on two true distributions that the wind power is assumed to follow in practice. 4.1. Data A wind power plant is considered in this study and its installed capacity is 200MW. Looking at the 24-hour bid- ding scheme, the expectations of the day-ahead hourly wind power forecast can be obtained from [15]. Although the real distribution of wind power is not necessarily known, two commonly used distributions including normal distribution and uniform distribution are supposed to be followed by the real output of plant. And we select 10% of the expectations as standard deviations ( ) under normal distribution to calculate the variation ranges which guarantee that wind power fluctuates within the installed capacity in real time. Then the support of distribution can be calculated according to , . The prices used for this study are taken from the electricity market of Spanish [16]. 4.2. Results Based on the data described above, the optimal bidding quantity under the minimax regret criterion, according to (10), can be calculated hourly by assessing conditions involving both of the prices and the limited information of wind power distribution. In order to investigate the effectiveness of the proposed bidding strategy, one possible way is to calculate the profit loss under a certain distribution of wind power from not making the optimal solutions. That is to make a comparison between the expected profits obtained with the proposed strategy ( ) and the optimal profits with full knowledge of the wind power distribution ( ). Comparisons including the expected profits, the profit losses and the profit loss ratios along the whole period are displayed in Table 1. It can be seen there that the optimal profits with full knowledge of wind power distribution are larger than the expected profits obtained with the proposed strategy. Profit losses and the ratios are defined as: ()( ) *o Profit LossERpERp = − (16) ( ) o Profit Loss Ratio ERp = (17) Results in Table 1 show that, despite the lack of information of wind power distribution, the expected profit 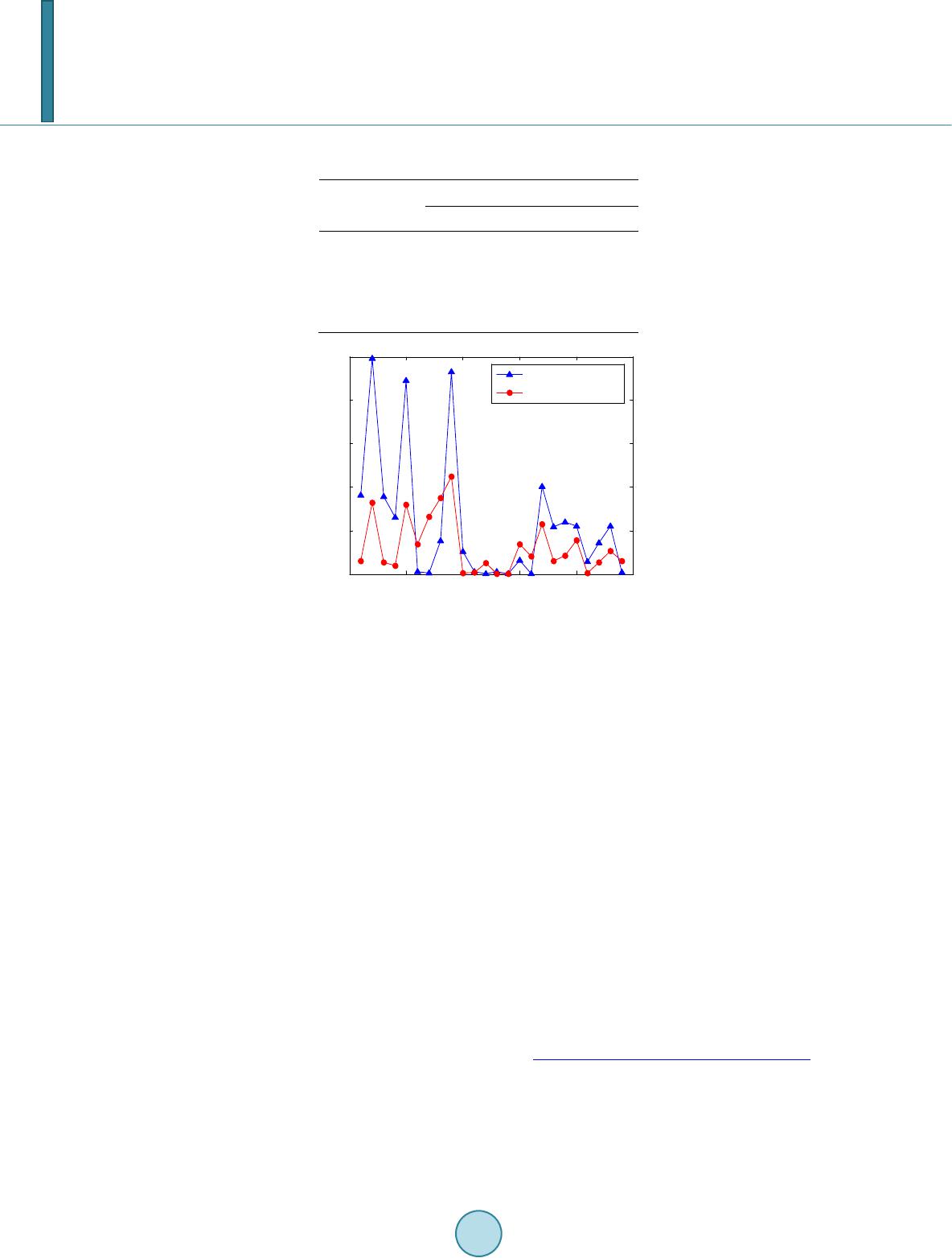 Y. S. Mao et al. Table 1. Profit loss of an entire day under normal dis- tribution and uniform distribution of wind power. Calculation Items Wind Power Distribution Normal Uniform (€) 54626.7 54328.3 (€) 54881.8 54501.9 Profit Loss (€) 255.1 173.6 Ratio (%) 0.4648 0.3185 Figure 1. Profit Loss calculated hourly under the nor- mal distribution and uniform distribution of wind power. with proposed bidding strategy in Section 3 is very close to the maximum expected profit when gaining full knowledge of the distribution. Although only two commonly used distributions are introduced to act as the real wind power distribution, the results, to a great extent, indicate the effectiveness of this bidding strategy. Ratios of the hourly profit loss under the above two wind power distributions are also plotted in Figure 1, which illustrates the superiority of the bidding strategy under the uncertainty of wind power distribution in every trading hour. 5. Conclusion This paper discusses the wind power bidding problem in day-ahead electricity market with limited distribution information of wind power. The optimal bidding problem is formulated into the expected profit. Suppose the expectation and variation range of wind power are the partial distribution information that can be predicted ac- curately, an optimal bidding strategy is adopted by applying the minimax regret criteria. Results from the model and case study reveal it a promising strategy. References [1] Galloway, S., Bel l, G., Burt, G., McDonald, J. and Siewierski, T. (2006) Managing the Risk of Trading Wind Energy in a Competitive Market. IEEE Proceedings of Generation, Transmission and Distribution, 153, 106-114. [2] Matevosyan, J. and Soder, L. (2006) Minimization of Imbalance Cost Trading Wind Power on the Short-Term Power market. IEEE Transactions on Power System, 21, 1396-1404. http://dx.doi.org/10.1109/TPWRS.2006.879276 [3] Zhang, X. (2012) Optimal Wind Bidding Strategy Considering Imbalance Cost and Allowed Imbalance Band. IEEE, EnergyTech, 1-5. [4] Zhang, H., Gao, F., Wu, J., Liu , K. and Zhai, Q. (2011) A Stochastic Cournot Bidding Model for Wind Power Produc- ers. IEEE International Conference on Automation and Logistics (ICAL), Chongqing, August 2011, 319-324. [5] Fabbri, A. , Gomez San Roman, T., Riv er Abbad, J. and Mendez Quezada, V.H. (2005) Assessment of the Cost Asso- 0510 15 20 25 0 0. 5 1 1. 5 2 2. 5 Hour Profit Loss Ratio (%) normal distribution uniform distribution  Y. S. Mao et al. ciated with Wind Generation Prediction Errors in a Liberalized Electricity Market. IEEE Transactions on Power Sys- tem, 20, 1440-1446. [6] Usaola, J. and Moreno, M.A. (2009) Optimal Bidding of Wind Energy in Intraday Markets. 6th International Confe- rence on the European Energy Market, 1-7. [7] Bueno, M., Moreno, M. A., Usaola, J. and No gales, F.J. (2010) Strategic Wind Energy Bidding in Adjustment Markets. 45th International IEEE Universities Power Engineering Conference (UPEC), August 2010, 1-6. [8] Hill, A.V. (2011) The Newsvendor Problem. Minneapolis: Clamshell Beach Press. [9] Zhu, Z., Zhang, J. and Ye, Y. (2006) Newsvendor Optimization with Limited Distribution Information. Working Paper, Stanford University, Stanford. [10] Natarajan, K., Shi , D. and Toh, K.C. (2012) A Probabilistic Model for Minmax Regret in Combinatorial Optimization. Working Paper, Singapore University of Technology and Design. [11] Yue, J., Chen, B. and Wang, M.C. (2006) Expected Value of Distribution Information for the Newsvendor Problem. Operations Research, 54, 1128-1136. http://dx.doi.org/10.1287/opre.1060.0318 [12] Perakis, G. and Roels, G. (2006) Regret in the Newsvendor Model with Partial Information. Working Paper, Opera- tions Research Center, Massachusetts Institute of Technology. [13] Xue, Y., Ve nkates h, B. and Chang, L. (2008) Bidding Wind Power in Short-Term Electricity Market Based on Mul- tiple-Objective Fuzzy Optimization. Canadian Conference on Electrical and Computer Engineering (CCECE 2008), 4-7 May 2008, 1135-1138. [14] Ramana, M.V., Tuncel, L. and Wolkowicz, H. (1997) Strong Duality for Semidefinite Programming. SIAM Journal on Optimization, 7, 641-662. http://dx.doi.org/10.1137/S1052623495288350 [15] Al-Awami, A.T. and El-Sharkawi, M.A. (2011) Coordinated Trading of Wind and Thermal Energy. IEEE Transactions on Sustainable Energy, 2, 277-287. http://dx.doi.org/10.1109/TSTE.2011.2111467 [16] (2014) Web of the Information System of the Spanish TSO. http://www.esios.ree .es/web-publica/
|