 Journal of Power and Energy Engineering, 2014, 2, 120-129 Published Online April 2014 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2014.24018 How to cite this paper: Aredes, M.A., França, B.W. and Aredes, M. (2014) Fuzzy Adaptive P&O Control for MPPT of a Photovoltaic Module. Journal of Power and Energy Engineering, 2, 120-129. http://dx.doi.org/10.4236/jpee.2014.24018 Fuzzy Adaptive P&O Control for MPPT of a Photovoltaic Module Maynara A. Aredes, Bruno W. França, Maurício Aredes Departament of Electrical Engineering,Federal Universityof Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil Email: maynara@lemt.ufrj.br, bruno@lemt.ufrj.br, aredes@lemt.ufrj.br Received December 2013 Abstract In this work a Maximum Power Point Tracker (MPPT) for photovoltaic modules is developed using fuzzy logic. As it is well known, the output of the photovoltaic module is a non-linear curve which has a unique point of maximum power (MPP) for a given condition of radiation and temperature. When a load is connected to the module, only in very specifics cases, the operation point will coin- cide with the MPP, for any other conditions the system will not operate with maximum power. Thus MPPT circuits must guarantee that photovoltaic modules operate with its maximum power at most of the time, independently to the radiation and temperature conditions. In order to achieve this objective, in this paper the input variables of the controller are transformed into lin- guistic variables, which associate with a set of rules results the displacement of the operation point so as to transfer the maximum power from the photovoltaic module to the load. Keywords Fuzzy Logic; MPPT; Photovoltaic Systems; Solar Cell 1. Introduction The photovoltaic generation of electrical energy has been widely discussed in the scientific community, in which a large number of papers have been published, increasing the knowledge about this subject. The photovoltaic technological growth is being achieved due to the following aspects: the enhancement of the photovoltaic cell material and the rise of the renewable sources. Both aspects agree with the current ecological trends, stimulated by the limited availability of the nonrenewable resources such as petroleum, natural gas, etc. The power electronic development has enabled the use of the photovoltaic energy, especially in the connec- tion between this source to the grid (AC systems) and to control the voltage and current to feed a specific load (DC system). In the second case, DC-DC converters are applied between the source and the load, aiming to guarantee the desired feeding aforementioned and also to achieve the maximum energy transfer to the load. In this way, many resources have been published [1-6], in order to obtain the Maximum Power Point Tracking (MPPT). In this work, a control method using Fuzzy logic is presented, applied to a buck-boost converter to perform a MPPT in DC systems. The effectiveness of the control method is verified through simulation analyses. 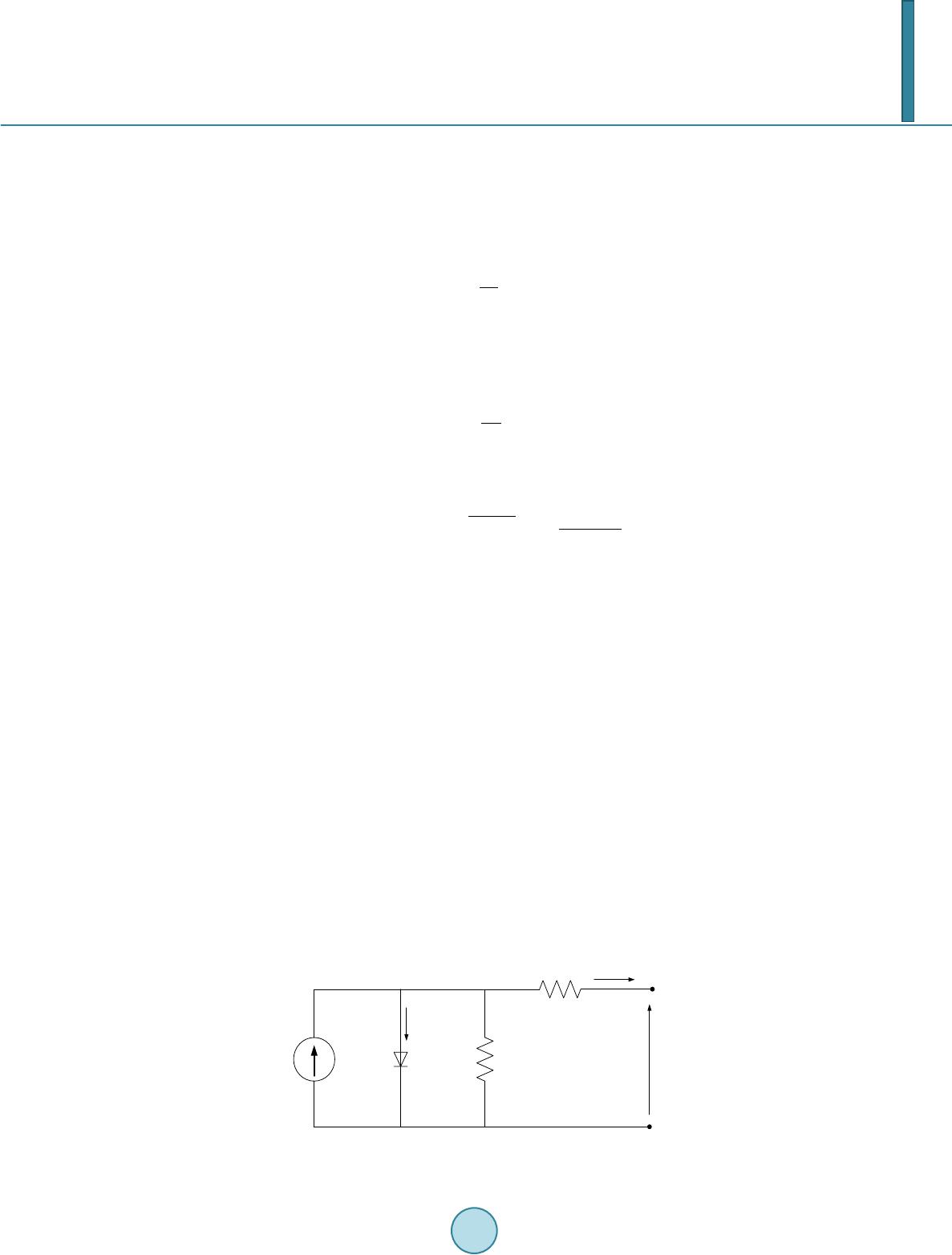 M. A. Aredes et al. 2. Mathematical Model of a Solar Panel The mathematical model of a solar cell can be obtained analyzing the simplified equivalent circuit of Figure 1. In this circuit the solar panel is represented by a current source in parallel to a diode and its series and parallel equivalent resistances [1]. The characteristic equation of the diode which describes the relation between current and voltage is given by (2). (1) where is the diode current, is the reverse bias saturation current of the diode, is the voltage across the diode, is the ideality factor of the diode and is the thermal voltage. The thermal voltage, has the function as shown in (2). (2) where k is the Boltzman constant Tis cell’s operating temperature in degree Kelvin and q is the electron charge. Using the diode equation (1) the relation between current and voltage of the circuit of Figure 1 is: ( ) 01 PV S T V IR nV PV S PV P V IR II IeR + + = −−− (3) where and are the current and output voltage of the circuit, is the current generated by the solar panel, and are the series and parallel equivalent resistances of the circuit, respectively. In real cells, is about and the parallel resistance more than . Thus, the function that describes the relation between the current and voltage of the solar cell depends on both the internal characteristics, and resistances, and external parameters such as temperature and intensity of solar radiation. In normal conditions the temperature is considered to be 25˚C, and the solar radiation is equal to 1000 W/m². Figures 2 and 3 show the variation of the characteristic curve for different values of temperature and radiation. 3. MPPT (Maximum Power Point Tracking) The output power of the solar cell can be estimated analyzing the curvesVxI in Figures 2 and 3. Figure 2 de- picts the curves VxI for different values of temperature and Figure 3 depicts the curves VxI for different values of solar radiation. In these figures, the maximum power points are highlighted for each curve. It is important to emphasize that for a constant solar radiation, as lower is the temperature the higher is the power will be supplied at the MPP. Otherwise, for a constant temperature, as higher is the solar radiation higher power will be supplied at the MPP. These characteristics are displayed is Figures 4 and 5, respectively. Both the solar radiation and the solar cell temperature are not constant throughout the day. In this way, a dy- namic MPPT controller is desired to optimize the solar cell power delivery. In order to obtain the higher VxI product, the MPPT controller is a closed loop controller embedded in a power electronic device to regulate the Figure 1. Equivalent circuit.  M. A. Aredes et al. Figure 2. I × V curve for different values of temperature. Figure 3. I × V curve for different values of solar radiation. Figure 4. P × V curve for different values of temperature.  M. A. Aredes et al. Figure 5. P × V curve for different values of solar radiation. output voltage. Therefore, the use of a power electronic device increases the total cost and may be not necessary depending on the load requirements. Thus, the MPPT control technology should be applied in special loads and/or complex electrical systems which justify its usage costs. 4. Buck-Boost Converter The buck-boost converter is widely used in photovoltaic systems, being responsible for the voltage regulation at the load bus. The output voltage can be controlled by this converter varying the duty cycle of the semiconductor switch (Figure 6). Controlling the output voltage, the energy transfer from the solar cell to the load can be regulated. The rela- tion between the load voltage , the source voltage , and the switch duty-cycle (D) is given by: (4) 5. Proposed P&O Control Using Fuzzy Logic The Perturb and Observe method (P&O) is one of the simplest and common control method to employ in pho- tovoltaic systems. It consists of increasing or decreasing the output voltage of the DC-DC converter by a fixed step value to achieve the MPP. The active power flow Pout(k) is calculated for each voltage variation and the new power value is compared to the last one Pout(k-1). If the Pout(k) is higher than Pout(k-1), then the next voltage variation will be kept in the same direction, otherwise it will go to the opposite direction. Usually the voltage step value is fixed around less than 1% of the output voltage Vout. Moreover, in ac- tual equipment, the voltage perturbation occurs with the same microcontroller sampling frequency and thus the MPPT is not achieved. In order to go with the MPPT and keep the P&O control advantages, recent studies have been focus on adap- tive control methods. One of these methods employs the fuzzy logic technique [1-4]. The adaptive control method using Fuzzy logic enhances the flexibility of the control, by varying the voltage step value. For a small value of the control dynamic is slow, however for large step values there is a high- er oscillation around the maximum power point, which can result in an undesired unstable condition. In this manner, the Fuzzy logic acts to adjust properly the amplitude to guarantee fast dynamic in transitory re- sponse, and also reduced power oscillation with satisfactory robustness in steady-state to goal with the MPPT. The proposed control method has two input signals and one output signal, as depicted in Figure 7. The inputs are the measured load voltage and current, and the output is the switch duty-cycle signal. The controller is com- posed by three main procedures: the Fuzzification, the Inference and the Deffuzification. 5.1. Fuzzification The Fuzzification is a procedure to transform real scalar values (crisp values) into fuzzy values. Fuzzy values  M. A. Aredes et al. Figure 6. Buck-boost converter. Figure 7. Input and output signals of the Fuzzy Controller. are grades classifications which composes sets of membership functions. Therefore, the inputs and outputs are used to calculate the voltage and power variation: (5) (6) where is the present measured output voltage and is the last sampling measured output voltage. The power variables and are obtained through the VxI product of the present and last sampling measured voltages and current signals, respectively. Both resultant signals ( and ) and the output variable (duty cycle variation of the converter) are divide in five categories: big negative (BN), small negative (SN), zero (Z), small positive (SP), big positive (BP). The membership functions were chosen intuitively, as shown in Figure 8. All variables were normalized by nominal operating values of known conditions of temperature and solar radiation. 5.2. Inference Table 1 and Figure 9 show the set of rules of the Fuzzy controller. All the inputs are Fuzzy variables: voltage variation , power variation and duty cycle variation (output of the controller). The inference Fuzzy method used was the Mandami method with max-min composition operation. 5.3. Defuzzification The output variable of the Fuzzy controller is a numerical variable, thus a defuzzification method is needed. The Centroid defuzzification method was chosen to transform the linguistic output into a physical variable (duty cycle of the buck-boost converter). The method is given by Equation (7), thus obtaining the amount of duty cycle that will be added to the previous value. Therefore the output voltage of the buck-boost converter will vary seeking the maximum power point. ( ) ( ) * . . C C zz dz zz dz µ µ = ∫ ∫ (7) 6. Simulation Results In order to verify the proposed controller performance, a MATLAB Simulink simulation was done. Figure 10 depicts the system simulation, which is composed of the power circuit and the controller. The power circuit has a PV module with 18 solar cells in series and 10 in parallel. This PV inputs a buck-boost converter which supplies a resistive load of 0.5 Ω. The Fuzzy adaptive P&O controller is mainly composed of: low-pass filters, to mitigate the high frequency components of the measured signals (current and  M. A. Aredes et al. Figure 8. Funções de pertinência das variáveis de entrada (ΔVeΔP) e de saída (ΔD). Figure 9. Fuzzy surface. 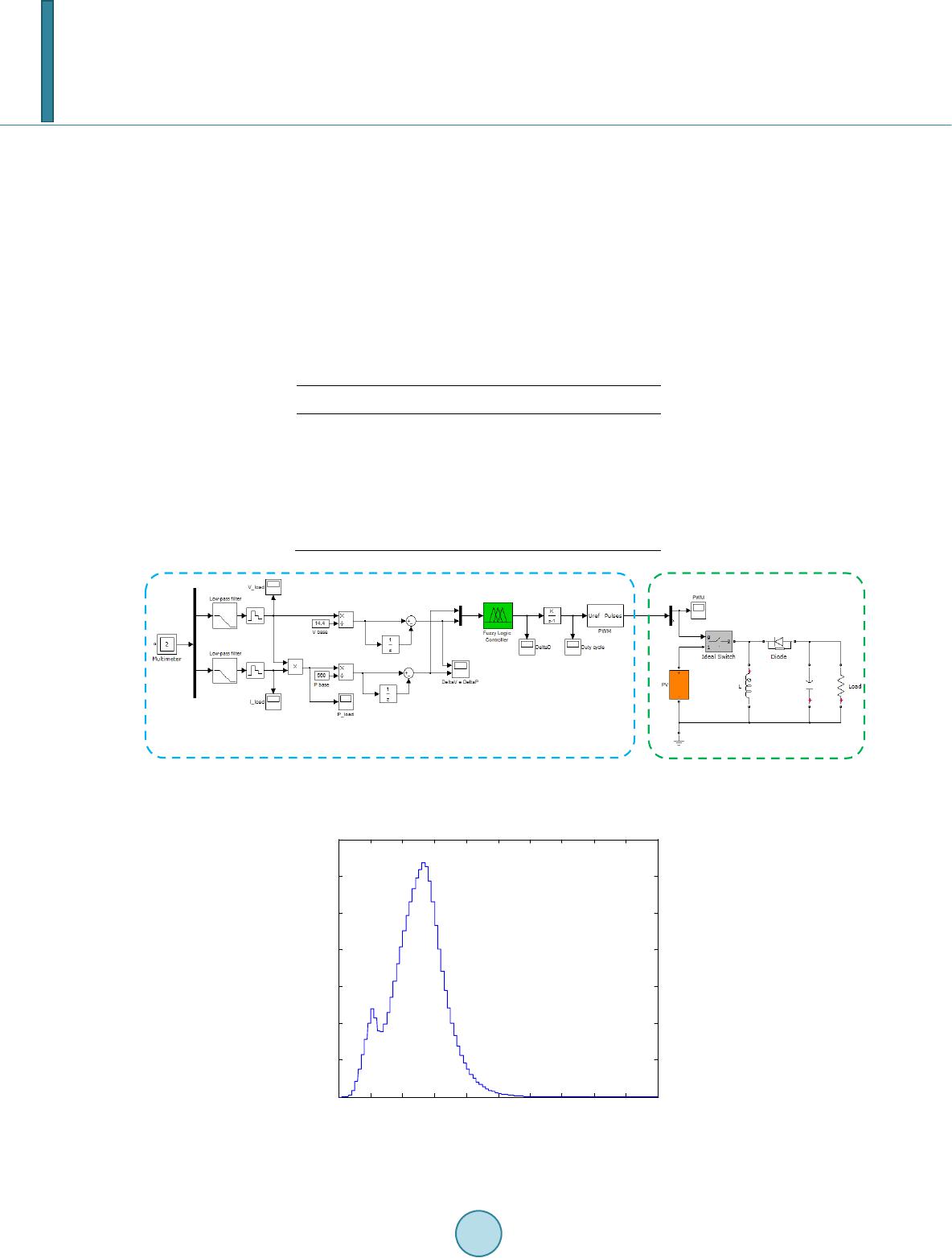 M. A. Aredes et al. voltage of the load); Fuzzy controller; and the PWM block. The Fuzzy block inputs are presented in Figures 11 and 12. According to the set of rules of the Fuzzy con- troller The MPP is achieved when both and are zero. Moreover, the dynamic response of the con- troller is shown in Figure 13 (output signal ), where the steady state is achieved in 2.5ms. Note that, at this time the power supplied by the PV module accomplished the maximum power point (Figure 14) at 13V (Figure 15) and duty cycle equal to 0.3 (Figure 16). 7. Conclusions A novel MPPT controller for photovoltaic systems was proposed using Fuzzy logic to achieve better perfor- mance in tracking the maximum power point of the solar cells. Table 1. Set of Rules. NG NP Z PP PG NG PG PP NP NP NG NP PP PP PP NP NP Z PP PP Z NP NP PP NP NP PP PP PG PG NG NP NP PP PG Figure 10. MATLAB Simulink simulation. Figure 11. Input signal ΔP of the Fuzzy controller. 00.5 11.5 22.5 33.5 44.5 5 x 10 -3 0 0. 005 0. 01 0. 015 0. 02 0. 025 0. 03 0. 035 time (s) DeltaP (p.u.)  M. A. Aredes et al. Figure 12. Input signal ΔV of the Fuzzy controller. Figure 13. Output signal ΔD of the Fuzzy controller. Figure 14. Load power. 00.5 11.5 22.5 33.5 44.5 5 x 10 -3 0 0. 005 0. 01 0. 015 0. 02 0. 025 0. 03 0. 035 0. 04 time (s) DeltaV (p.u.) 00.5 11.5 22.5 33.5 44.5 5 x 10 -3 -0.01 -0.005 0 0. 005 0. 01 0. 015 0. 02 0. 025 0. 03 time (s) DeltaD 00.5 11.5 22.5 33.5 44.5 5 x 10 -3 0 50 100 150 200 250 300 350 time (s) Load Power (W)  M. A. Aredes et al. Figure 15. Load voltage. Figure 16. Duty cycle. The set of rules of the controller were designed to vary the duty cycle variation, different from the classical P&O controller. Simulation results verified the efficiency of the controller, highlighting the fast response and good dynamic of the system. References [1] Xiao, W. and Dunford, W. (2004) A Modified Adaptive Hill Climbing MPPT Method for Photovoltaic Power Systems. IEEE Power Electronics Specialists Conference, 3, 1957-1963. [2] Won, C.-Y., Kim, D.-H., Kim, S.-C., Kim, W.-S. and Kim, H.-S. (1994) A New Maximum Power Point Tracker of Photovoltaic Arrays Using Fuzzy Controller. 25th Annual IEEE Power Electronics Specialists Conference, 1, 396-403. [3] Mohd Zainuri, M., Mohd Radzi, M., Soh, A. a nd Ra him, N. (2012) Adaptive P& O-Fuzzy Control MPPT for PV Boost dc-dc Converter. 2012 IEEE International Conference on Power and Energy (PECon), Kota Kinabalu, 2-5 December 2012, 524-529. [4] Kuo, Y.-C., Liang, T.-J. and Chen, J.-F. (2001) Novel Maximum-Power-Point-Tracking Controller for Photovoltaic Energy Conversion System. IEEE Transactions on Industrial Electronics, 48, 594-601. [5] Femia, N., Petrone, G., Spagnuolo, G. and Vitelli, M. (2005) Optimization of Perturb and Observe Maximum Power Point Tracking Method. IEEE Transactions on Power Electronics, 20, 963- 973. [6] Esram, T. and Chapman, P. (2007) Comparison of Photovoltaic Array Maximum Power Point Tracking Techniques. Energy Conversion, 22, 439-449. http://dx.doi.org/10.1109/TEC.2006.874230 00.5 11.5 22.5 33.5 44.5 5 x 10 -3 -2 0 2 4 6 8 10 12 14 time (s) Load voltage (V) 00.5 11.5 22.5 33.5 44.5 5 x 10 -3 -0.05 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 time (s) Duty Cycle  M. A. Aredes et al. [7] Chim, C., Neelakantan, P., Yoong, H. and Teo, K.T.K. (2011) Fuzzy Logic Based MPPT for Photovoltaic Modules In- fluenced by Solar Irradiation and Cell Temperature. 13th International Conference on Computer Modelling and Simu- lation (UKSim), Cambridge, 30 March-1 April 2011, 376-381. [8] Chin, C.S. , Chin, Y.K., Chua, B.L., Kiring, A. a nd Teo, K. (2012) Fuzzy Logic Based MPPT for PV Array under Par- tially Shaded Conditions. 2012 International Conference on Advanced Computer Science Applications and Technolo- gies (ACSAT), Kuala Lumpur, 26-28 November 2012, 133-138.
|