Paper Menu >>
Journal Menu >>
 HEALTH, 20 09, 1, 2-7 Published Online June 2009 in SciRes. http://www.scirp.org/journal/health Finite element analysis of a percutaneous aortic valve stent design Gideon Praveen Kumar1*, Lazar Mathew1 1School of Biotechnology, Chemical & Biomedical Engineering, VIT University, Vellore, India. *Corresponding author: Tel: +919894292348, Email: gidi99_5611@yahoo.co.in Received 15 April 2009; revised 28 April 2009; accepted 30 April 2009. ABSTRACT Aim: This paper discusses the design and Finite Element Analysis (FEA) of a Percutaneous Aor- tic Valve Stent. The aim of this study was to model a percutaneous aortic valve stent and subject it to finite element analysis. The design process was carried out to meet the functional and surgical requirements. Methods and Results: Analysis was done with different materials with loads ranging from 50 kgf/mm² to 73 kgf/mm². These forces were selected because these val- ues are far greater than the normal human blood pressure which ranges from 10kPa to 16kPa. It was also to understand the mechanical behavior of different stent materials under such high pressures. A stent model was generated and its physical, mechanical and behavioral properties were studied. Finite element analysis and simulation of the model enhanced the designer to optimize the geometry suitable for perform- ance during and after implantation. The design objective for the stent is to have long term du- rability, low thrombogenicity, resistance to mi- gration and paravalvular leak. Conclusion: The analysis performed in this paper may aid in understanding the stent’s tolerable pressures ranges in comparison with the physiological pressures exerted by the heart and cardiac blood flow during abnormal cardiovascular conditions. Keywor ds: stent; finite element analysis; blood flow; aortic valve stenosis; port size 1. INTRODUCTION The treatment of stenotic valvular diseases consists of routine procedures in interventional cardiology. To date, surgical approach is the only option to replace diseased cardiac valves. Recently stenosis of mitral, aortic or pulmonary valves is treated by percutaneous valve re- placement and has opened new perspectives on tran- scatheter placement of cardiac valves. Aortic valve re- placement was generally accomplished by using open heart valve surgery, whereas endovascular procedures for valve replacement may provide an alternative to car- diac surgery. Such endovascular procedures require minimal invasion of the human body, and there is con- siderable reduction and, in some instances, even elimi- nation of general anesthesia and intensive care unit stay. In Percutaneous replacement, the diseased valve is re- placed by a biological valve (porcine) via a catheter driven through the femoral artery to the aortic position. The valve is mounted on the stent, which is crimped into the catheter and is guided to the parent position of the aorta and deployed. Thus it pushes the diseased valve aside to position itself. Post operative complications are very minimal and the patient can get discharged within days after the procedure. The stents that are used give adequate support and stability to the valve and also pre- vent the valve from getting migrated either in the ante grade or retro grade direction. These stents also help in preventing paravalvular leaks. So modeling of an ideal stent design was done and the subjected to finite element analysis with loads much greater than the expected blood pressures even during adverse conditions. 2. STENT DESIGN The design of the stent depends on many unique pa- rameters, which include stent length, stent diameter, number of struts, strut diameter and port angle. The de- sign was an attempt to model a stent which would be an ideal partner to the tissue valve that replaces the diseased one [1]. Solid 3D models (Figure 1) were created using repeating unit geometry of each design using Solidworks Modeling Software. The unit consisted of 8 lips with two non crossing struts making a circular diameter of 16mm. Two struts join to form a lip creating a diamond shaped port. The port angle is 45 degrees and the distance be- tween the two struts at the center is 6.25mm, with 8 lips joining at the center to form the circular stent. The stent design has a constant strut thickness of 0.5 mm and a height of 18 mm.  G. P. Kumar et al. / HEALTH 1 (2009) 2-7 3 SciRes Copyright © 2009 HEALTH STENT DIA 16mm WIRE DIA 0.5MM 18 mm 9 mm 45 degree Figure 1. Model geometry of the stent. 3. MATERIAL MODEL Stainless steel 316L was the material that was used for analysis as it has a high strength to weight ratio and excellent biocompatibility when used in humans [6]. The material properties ideal for analysis are tabulated in Table 1. The material properties were assumed to be bilinear, elasto-plastic model with isotropic hard- ening. All materials were also assumed to follow Hooke’s Law, and frictional forces neglected due to the magnitude of this force being much less than the applied force. The implant was assumed to transmit all absorbed energy to the surrounding environment. The amount of energy transfer to and from the implant is zero. The effects due to body heat were also ne- glected to optimize effects. 4. FINITE ELEMENT ANALYSIS Finite element analysis with 316L stainless steel was performed using visual Nastran, a FEA package. Visual Nastran, a powerful general purpose finite element analysis solution for small to complex assemblies, was used for the entire analysis [6]. Stresses ranging between 50 kgf/mm2 and 73 kgf/mm2 were loaded on to the stent in the transverse direction. These pressures were selected as they are far greater than that of the normal human blood pressure which ranges from 10kPa to 16kPa. Ini- Table 1. List of properties used for analysis. Material Name 316 L Stainless Steel Young’s modulus (E) 201 GPa Poisson’s ratio 0.3 Yield stress 170 MPa tially the loads were given as a centripetal pressure around the circular stent in the transverse direction. The reason for choosing this direction is because of the fact that the pulsatile contraction of the aorta is in the same direction. The model was constrained to- wards one end of the stent. Owing to the direction of load application and the stent being constrained to- wards one end, the stent was able to crimp and re-expand without stent fracture even when the load applied was far greater than that of the normal physio- logical pressures. The model was then constrained towards the lower end of the stent. The upper portion of the stent is somewhat free and is along the longitu- dinal axis of the ascending aorta and the lower portion bears the aortic valve and is fixed to the aortic annulus. Similar pressures were applied in the upward direction to understand the mechanical and physical behavior of the stent. In the same position, pressures were applied in the downward direction to understand the behavior 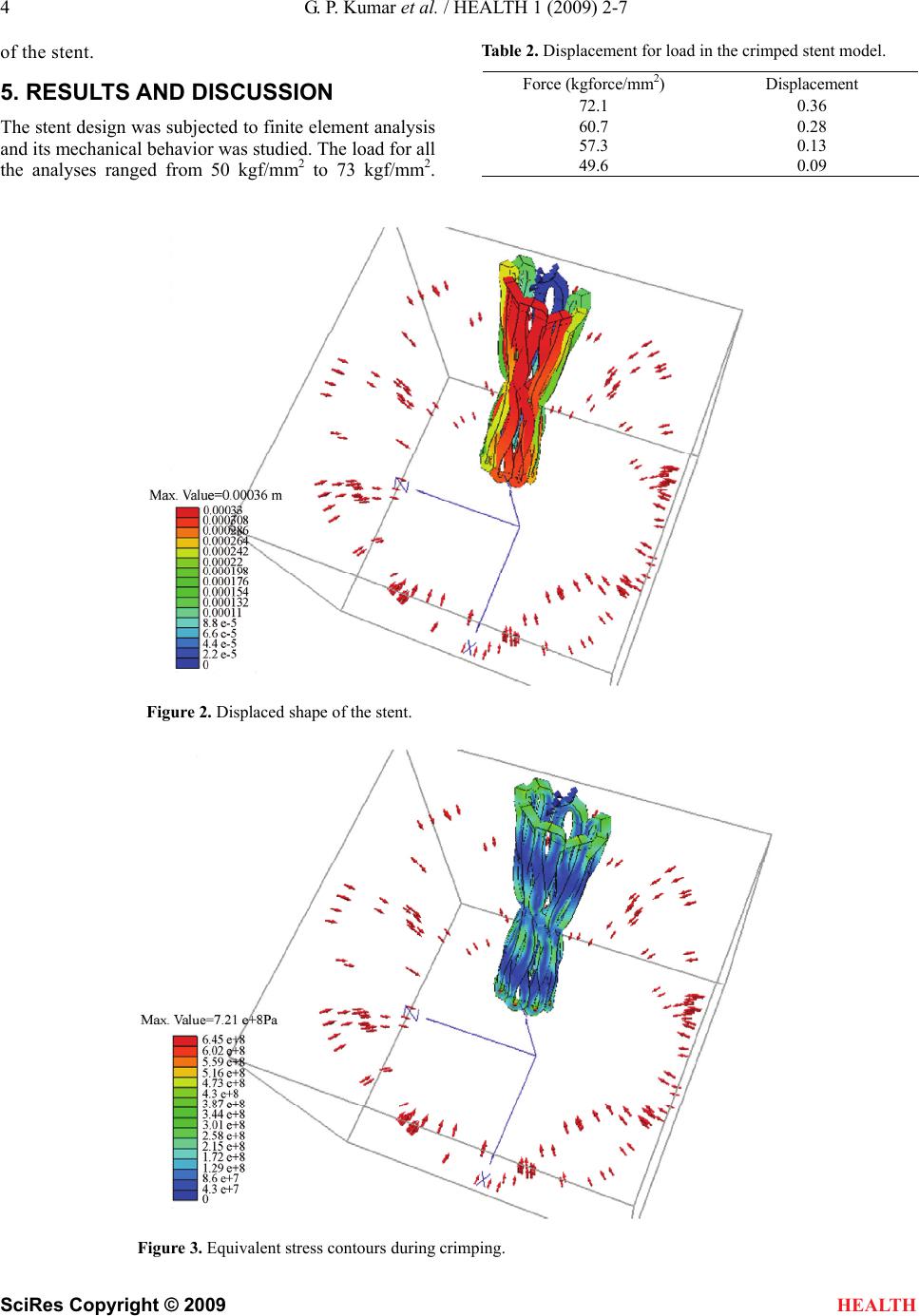 4 G. P. Kumar et al. / HEALTH 1 (2009) 2-7 SciRes Copyright © 2009 HEALTH of the stent. 5. RESULTS AND DISCUSSION The stent design was subjected to finite element analysis and its mechanical behavior was studied. The load for all the analyses ranged from 50 kgf/mm2 to 73 kgf/mm2. Table 2. Displacement for load in the crimped stent model. Force (kgforce/mm2) Displacement 72.1 0.36 60.7 0.28 57.3 0.13 49.6 0.09 Figure 2. Displaced shape of the stent. Figure 3. Equivalent stress contours during crimping. 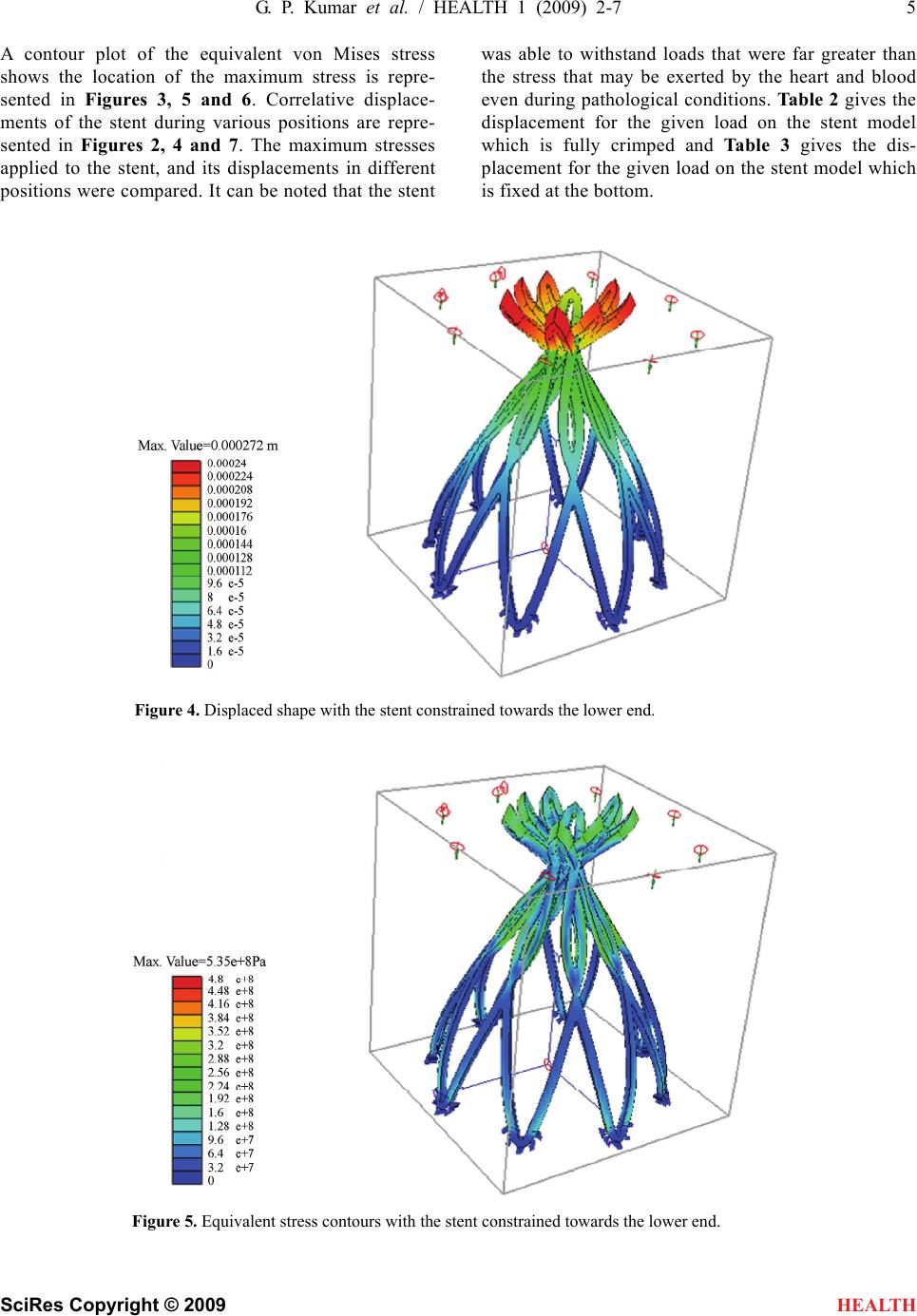 G. P. Kumar et al. / HEALTH 1 (2009) 2-7 5 SciRes Copyright © 2009 HEALTH A contour plot of the equivalent von Mises stress shows the location of the maximum stress is repre- sented in Figures 3, 5 and 6. Correlative displace- ments of the stent during various positions are repre- sented in Figures 2, 4 and 7. The maximum stresses applied to the stent, and its displacements in different positions were compared. It can be noted that the stent was able to withstand loads that were far greater than the stress that may be exerted by the heart and blood even during pathological conditions. Table 2 gives the displacement for the given load on the stent model which is fully crimped and Table 3 gives the dis- placement for the given load on the stent model which is fixed at the bottom. Figure 4. Displaced shape with the stent constrained towards the lower end. Figure 5. Equivalent stress contours with the stent constrained towards the lower end. 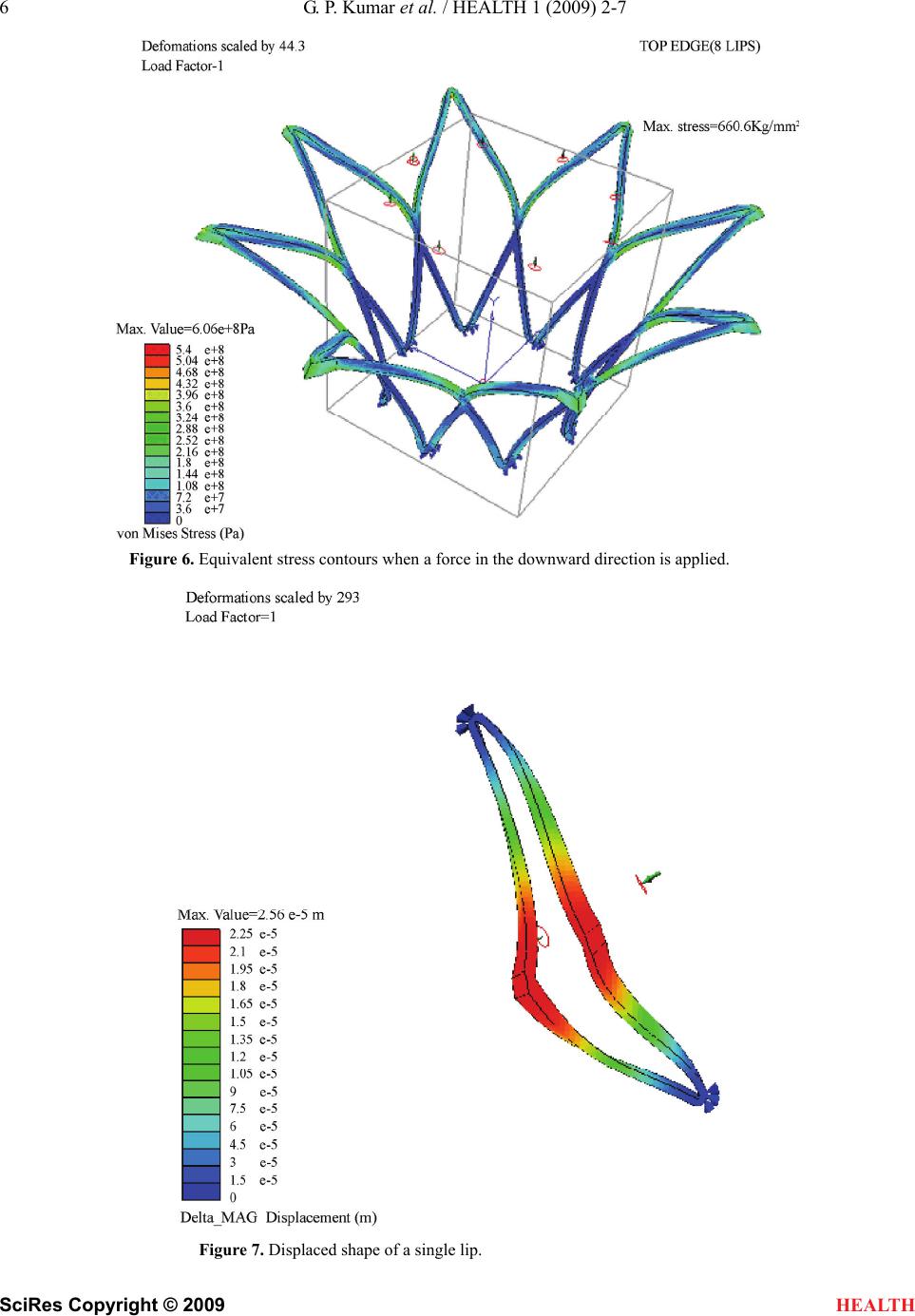 6 G. P. Kumar et al. / HEALTH 1 (2009) 2-7 SciRes Copyright © 2009 Figure 6. Equivalent stress contours when a force in the downward direction is applied. Figure 7. Displaced shape of a single lip. HEALTH  G. P. Kumar et al. / HEALTH 1 (2009) 2-7 7 SciRes Copyright © 2009 Table 3. Displacement for load in the stent model fixed at the bottom. Force (kgforce/mm2) Displacement (mm) 53.5 0.27 47.2 0.22 43.7 0.16 38.1 0.11 HEALTH 6. CONCLUSION The stent design modeled and subjected to Finite ele- ment analysis proved to be having ideal behavior for percutaneous replacement by withstanding loads that are well above the required level. The displacement was good enough to prove mild contractions during cardiac systole and diastole. REFERENCES [1] C. M. Allison, D. Crossman, and J. Gunn, (2004) The influence of physical stent parameters upon restenosis, Elsevier SAS. [2] K. W. Lau, A. Johan, U. Sigwart, and J. S. Hung, (2004) A stent is not just a stent: stent construction and design do matter in its clinical performance, Singapore Medical Journal. [3] D. R. McClean and N. Eigler, (2002) Stent design: Im- plications for restenosis, MedReviews, LLC. [4] (2004) Stent design properties and deployment ratio in- fluence indexes of wall shear stress: A three-dimensional computational fluid dynamics investigation within a normal artery, J Appl Physiol, 97, 424-430. [5] (2000) An overview of superelastic stent design, Min Invas Ther & Allied Technol, 9(3/4), 235-246. [6] (2007) Engineering aspects of stents design and their translation into clinical practice, Ann Ist super sAnItà, 43(1), 89-100. [7] (2005) To stent or not to stent aortic dissection:good news for a chosen few, but who? European Heart Journal, 26, 431-432, doi:10.1093/eurheartj/ehi119. [8] J. Q. Zhou, A. F. Corno, C. H. Huber, P. Tozzi, and L. K. von Segesser, (2003) Self-expandable valved stent of large size: off-bypass implantation in pulmonary position, Eur. J. Cardiothorac. Surg., 24(2), 212-216. [9] G . P. Kumar and L. Mathew, (2009) New stent design for percutaneous aortic valve replacement, International Journal of Cardiovascular Revascularization Medicine, 10(2), 121-124. |

