A Novel Solution Based on Differential Evolution for Short-Term Combined Economic Emission Hydrothermal Scheduling

doi:10.4236/eng.2009.11007

Paper Menu >>

Journal Menu >>

Engineering, 2009, 1, 1-54

Published Online June 2009 in SciRes (http://www.SciRP.org/journal/eng/).

A Novel Solution Based on Differential Evolution for

Short-Term Combined Economic Emission

Hydrothermal Scheduling

Chengfu Sun1, Songfeng Lu2

School of Computer Science and Technology,

Huazhong University of Science and Technology, Wuhan, China

Email: 1ajason509@smail.hust.edu.cn, 2lusongfeng@sina.com

Received April 17, 2009; revised May 13, 2009; acce pted May 18, 2009

Abstract

This paper presents a novel approach based on differential evolution for short-term combined economic

emission hydrothermal scheduling, which is formulated as a bi-objective problem: 1) minimizing fuel cost

and 2) minimizing emission cost. A penalty factor approach is employed to convert the bi-objective problem

into a single objective one. In the proposed approach, heuristic rules are proposed to handle water dynamic

balance constraints and heuristic strategies based on priority list are employed to repair active power balance

constraints violations. A feasibility-based selection technique is also devised to handle the reservoir storage

volumes constraints. The feasibility and effectiveness of the proposed approach are demonstrated and the test

results are compared with those of other methods reported in the literature. Numerical experiments show that

the proposed method can obtain better-quality solutions with higher precision than any other optimization

methods. Hence, the proposed method can well be extended for solving the large-scale hydrothermal sched-

uling.

Keywords: Hydrothermal Power Systems, Economic Load Scheduling, Combined Economic Emission

Scheduling, Differential Evolution

1. Introduction

One of the major problems existing today on electric

power systems is the optimum scheduling of hydrother-

mal plants. Short-term hydrothermal scheduling is a

daily planning task in power systems and its main objec-

tive is to minimize the to tal operational cost subjected to

a variety of constraints of hydraulic and power system

network. As the source for hydropower is the natural

water resources, the operational cost of hydroelectric

plants is insignificant. Thus, the objective of minimizing

the operational cost of a hydrothermal system essentially

reduces to minimize the fuel cost of thermal plants over a

scheduling horizon while satisfying various constraints.

Due to increasing concern over atmospheric pollution,

harmful emission produced by the thermal units must be

minimized simultaneously. So a revised economic power

dispatch program considering both the fuel cost and

emission is required. But minimizing pollution may lead

to an increase in generation cost and vice versa.

The importance of the generation scheduling problem

of hydrothermal systems is well recognized. Therefore,

many methods have been devised to solve this difficult

optimization problem for several decades. Some of these

methods are dynamic programming methodology [1],

linear programming [2], and decomposition techniques

[3]. Recently, aside from the above methods, optimal

hydrothermal scheduling problems have been solved by

meta-heuristic approaches such as genetic algorithm

[4-6], cultural algorithm [7] and particle swarm optimi-

zation [8] etc. Various heuristic methods such as heuristic

search technique [9], fuzzy satisfying evolutionary pro-

gramming procedures [10] and fuzzy decision-making

stochastic technique [11] have been applied to solve

C. F. SUN ET AL. 47

multi-objective short-term hydrothermal scheduling

problems. Because these meta-heuristic optimization

methods are able to provide higher quality solutions, they

have received more interest. One of these meta-heuristic

optimization method s is differential evolution (DE) [13].

A new optimization method known as DE, which is a

stochastic search algorithm based on population coopera-

tion and competition of individuals, has gradually be-

come more popular and has been successfully applied to

solve optimization problems particularly involving

non-smooth objective function. DE combines the simple

arithmetic operators with the classical evolution opera-

tors of crossover, mutation and selection to evolve from a

randomly generated population to a final solution. The

DE algorithm has been applied to various fields of power

system optimization such as dynamic economic dispatch

with valve-point effects [14], hydrothermal scheduling

[15], economic dispatch with non-smooth and

non-convex cost functions [16], optimal reactive power

planning in large-scale distribution system [17], and

economic dispatch problem [18].

This work presents a novel approach based on differ-

ential evolution to solve short-term combined economic

emission scheduling of cascaded hydrothermal systems.

Moreover, heuristic rules are proposed to handle the

water dynamic balance constraints and heuristic strate-

gies based on priority list are employed to handle active

power balance constraints. At the same time, a feasibil-

ity-based selection technique is devised to handle the

reservoir storage volumes constraints. The results ob-

tained with the proposed approach were analyzed and

compared with the results of the differential evolution

[12] and interactive fuzzy satisfying method based on

evolutio nary progra mming [10] reported in the literature.

The remainder of the paper is organized as follows.

The formulation of the short-term combined economic

emission scheduling of hydrothermal power systems

with cascaded reservoirs is introduced in Section 2, while

Section 3 explains the classical DE. Section 4 describes

the implementation of the proposed method for solving

the short-term hydrothermal scheduling and outlines

heuristic strategies to handle water dynamic balance

constraints and active power balance constraints. Section

5 presents the optimization results for the short-term

hydrothermal power systems scheduling. Lastly, section

6 draws the conclusions.

2. Problem Formulation

The hydrothermal scheduling problem combined eco-

nomic emission scheduling is formulated as a bi-objec-

tive optimization problem. It is concerned with the at-

tempt to minimize the fuel cost and as well as the emis-

sion of thermal units, while making full use of the avail-

ability of hydro-resources as much as possible. In the

formulation of the hydrothermal scheduling problem, the

following objectives and constraints must be taken into

account and the equality and inequality constraints must

simultaneously be satisfied.

2.1. Notations

In order to formulate the hydrothermal scheduling prob-

lem mathematically, the following notations is intro-

duced first:





it sit

P fuel cost of thermal plant including valve

point loading





it sit

eP emission of thermal plant i including valve

point loading

isisi

abc ,

isi

ef coefficients of thermal generating

plant

,,,

isisisisi





emission coefficients of thermal

plant

total time intervals over scheduling horizon

N, number of thermal and hydro plants respec-

tively h

hjt

P power generation of hydro generating plant

at time interval

P power generation of thermal generating unt i

at time interval i

P power demand at time intervalt

P total transmission loss at time interval t

123456

,,,,,

jjjj

CCCCCC

power generation coeffi-

cients of hydro plant

hjt

V storage volume of reservoir

at time interval t

hjt

Q water discharge rate of the

th reservoir at

time .

min

P minimum and maximum power genera-

tion by thermal plant

max

min

Pmax

P minimum and maximum power generation

by hydro plant

min ,

max

hj minimum and maximum storage volumes

of reservoir

hjt

at time interval inflow of hydro reservoir t

hjt

S spillage discharge rate of hydro plant

at time

interval



water transport delay from reservoir tom

R number of upstream hydro generating plants di-

rectly above reservoir

G current iteration generation

N number of the parameter vectors

2.2. Objective Functions

48 C. F. SUN ET AL.

generating unit with valve-point effects is considered.

2.2.1. Economic Scheduling

In this paper, non-smooth fuel cost function of therma







2min

sin

itsitsisi sitsi sitsisisisit

fPa bP cPefPP 

(1)

For a given hydrothermal system, the problem may be

described asinimization o total fuel cost associated to

the on-line N units for

intervals in the given time

horizon as defined by Equation (2) under a set of operat-

ing constraints as follo ws:

P (2)

the sum of a quadratic and an

exponential functio n.

amount of emis-

sion release defined by Equation(4) as

(4)

.3. Constraint s

follow-

inultaneously.

Active power balance constraint

(5)

ervoir water head, which can be

expressed as follows:



min []

it sit







2.2.2. Emission Sche duling

In this study, the amount of emission from each genera-

tor can be described as

 

exp

tsitsisi sitsi sitsisi sit (3)

The economic emission scheduling problem can be

expressed as the minimization of total

ePP PP

 

 



[]

it sit

EeP





While minimizing the above two objectives, the

g constraints must be satisfied sim

11ij

The hydroelectric generation is a function of water

discharge rate and res

sithjt Dt Lt

PPPP



12 345hjtjhjtjhjtj hjthjtjhjtjhjt6j

CV CQ CVQ CVCQC

(6)

Generation limits constraint

(8)

1) Reserv oi r st or age volume

(9)

2) Discharge rates limit

(10)

3) Water dynamic balance constraints



min max

sisit si

PPP (7)

min max

hjhjt hj

PPP

s constraints

min max

VVV

hj hjt

min max

hjhjt hj

QQQ



,1, ,

mj mj

hjthj thjthjthjthm thm t

VV IQSQS







 



(11)

3. Overview of Differential Evolution

Algorithm

As a population-based and stochastic global optimizer,

differential evolution (DE) is one of the latest evolution-

ary optimization methods proposed by Storn and Price

[13]. In a DE algorithm, candidate solutions are ran-

domly generated and evolved to final individual solution

by simple technique combining simple arithmetic opera-

tors with the classical events of mutation, crossover and

selection. One of the most frequently used mutation

strategies, named “DE/rand/1/bin”, will be employed in

this paper.

3.1. Mutation Operation

The essential ingredient in the mutation operation is the

vector difference. For each target vector,

the weighted difference between two randomly selected

vectors



1, 2,,

Xi N

and G

is added to a third randomly se-

lected vector G

to generate a mutated vector

using the following equation.



GG GG

ik lm

VXFXX 



(12)

whereG

and G

are randomly selected vectors and

ik l m



 ; The mutation factor is a user cho-

sen parameter to control t he amplification of the di fference

between two individuals so as to avoid search stagnation.

0F

3.2 Crossover Operation

Following the mutation phase, the crossover operation is

performed in order to increase the diversity in the

searching process.







ij j

ij G

Vif CRorjq

UXotherwise

















(13)

where





0, 1



, generated anew for each value of

, is

a uniformly distributed random number. The crossover

factor





0, 1CR

ij ij

controls the diversity of the popula-

tion. ,,

and , are the th parameter of the

th target vector, mutant vector and trial vector at gen-

eration , respectively.

3.3. Selection Operation

C. F. SUN ET AL. 49

Thereafter, a selection operator is applied to compare the

fitness function value of two competing vectors, namely,

target and trial vectors to determine who can survive for

the next generation.





UiffU fX

XXotherwise













(14)

where denotes the fitness function under optimization

(minimization).

4. Implementation of the Proposed Method

for Solving the Short-Term Hydrothermal

Scheduling

In this section, the procedures for solving short-term

scheduling problem of hydrothermal power system are

described in details. Especially, heuristic strategies will

be given to handle constraints of hydrothermal schedul-

ing problem. The process of the proposed method for

solving hydrothermal scheduling can be summarized as

follows.

4.1. Structure of Parameter Solution Vector

The structure of a solution for hydrothermal scheduling

problem is composed of a set of decision variables which

represent the discharge rate of the each hydro plant and

the power generated by each thermal unit over the

scheduling horizon.

11211 11211

12222 12222

12 12

hhhNss sN

hThThNTsTs TsNT

QQQ PPP

QQQPPP

QQQ PPP

















(15)

The elements and

hjt

P(1, 2,;

jNi



1, 2,,

N) are subjected to the water discharge rate and

the thermal generating capacity constraints as depicted in

Equation. (10) and (7), respectively. The water discharge

rate of the

th hydro plant in the dependent interval

must satisfy the water dynamic balance constraints in

Equation (11).

4.2. Initialization Parameter Vectors

During the initialization process, the candidate solution

of each parameter vector



1, 2,,

k





minmax min

hjt hjqhjhj

QQ rQQ (16)





minmax min

sit sissisi

PP rPP  (17)

where and are the random numbers uniformly dis-

tributed in





0,1 .

4.3. Combined Economic and Emission

Scheduling

The short-term combined economic emission scheduling

of hydrothermal power systems with cascaded reservoirs

is a bi-objective problem with the attempt to minimize

simultaneously fuel cost and emission of thermal plants.

The bi-objective optimization problem can be trans-

formed into a single objective one by introducing price

penalty factors. For more details, see Ref.

h[12].

4.4. Solution Modification

New values of water discharge rate and power

generation

,1hj t

Q



are generated through mutation and

crossover operation according to Equations (12) and (13),

respectively. The new values are not always guaranteed

to satisfy the constraints Equations (10) and (7), respec-

tively. If any value violating its constraint is modified in

the following way:

min min

min max

,1 ,1,1

max max

hjhj thj

hj thj thjhj thj

hjhj thj

QifQ Q

QQifQQQ

QifQ Q























(18)

min min

min max

,1 ,1,1

max max

sisi tsi

si tsitsisi tsi

sisi tsi

PifP P

PPifPPP

PifP P



 

















(19)

4.5. Heuristic Strategies to Handle Equality

Constraints

4.5.1. Handling Water Dynami c Bal ance Constraints

To meet exactly the restrictions on the initial and final

reservoir storage, the water discharge rate of theth

hydro plant in the dependent interval dis then calcu-

lated using Equation(21). The dependent water discharge

rate must satisfy the constraints in Equation (10). As-

suming the spillage in Equation (11) to be zero for sim-

plicity, the water dynamic balance constraints are

N is ran-

domly initialized within the feasible range as follows:



111 1

TT T

hjhjThjthm thjt

ttmt

VV QQI





 

 



 (20)

50 C. F. SUN ET AL.

where is the initial storage volume of reservoir;

is the final storage volume of reservoir. The pro-

cedures for repairing the water dynamic balance viola-

tions in hydrothermal scheduling are as follows:

0hj

V j

hjT

V j

Step 1: Set.

1j

Step 2: Randomly choose a time interval as a de-

pendent interval and setd

1count



Step 3: In order to meet equality constraint in Equation

(11), the water discharge rate of the

th hydro plant

in the dependent interval is then calculated by

hjd



111 1

TT T

hjdhjohjThjthm thjt

ttm t

QVVQQI





 



 



(21)

If the computed doesn’t violate the constraints in

Equation (10) then go to step 7; otherwise go to the next

step

hjd

Step 4: Cha n ge using Equation(18).

hjd

Step 5: A new random time interval is chosen en-

suring that it is not repeatedly selected

and .

1count count

Ste p 6 : I fcou , then go to step 3; otherwise go to

next step. nt T

Step 7: if , then go to step 2; other-

wise go to next step.

1,jj h

jN

Step 8: The modification process is terminated.

4.5.2. Handling Active Power Balance

Constraints

The power balance equality constraints in Equation(5)

still remain to be resolved after the water dynamic bal-

ance constraints are preserved. The heuristic strategy

based on priority list is proposed for handling the power

balance constraints. In this paper, priority list is created

according to each thermal plant parameter. When the

thermal plant is at its maximum output power, the aver-

age full-load cost it



of thermal plant at time interval

is defined by



max max

max

itsitit si

fP heP







 (22)

where is price penalty factor at time interval,



and 2



are the weight factors. The detail procedures

for handling active power balance constraints are as

follows:

Step 1: Calculate the average full-load cost it



using

Equation(22) at time intervalt. Arrange them in ascend-

ing order of it



to obtain a priority list.



PL t

Step 2: Set.

1t

Step 3: Set.

 

_tempPLtPL t

Step 4: The amount of active power balance violation

at time interval tis calculated

it hjt

tP PP



 

 Dt

. In this paper the

power loss is not considered for simplicity.

Step 5: If0





, go to Step 14; if, go to

Step 6; if

P



, go to Step 10.

Step 6: Set1m



Step 7: Set power of the generator unit with highest







_tempPL t

ktemp

to be .Then delete ther-

mal unit from.

mint

ksk

PP



t_PL

Step 8: Calculate the total power t

generated by

all thermal units at time intervalt. If

Phjt Dt







)

set and go to step 14;

otherwise s et.

min

(

ksihjtDt m

PP PP



 



mint

ksk

PP

Step 9 : 1mm



. If



, then go to Step 7; oth-

erwise go to Step 14

Ste p 10 : Se t1m



Step 11: Set power of the generator unit kwith low-

est







t to be.Then delete

thermal unit from.

_temp PL

ktemp

maxt

ksk

PP



_PL

Step 12: Calculate the total power

generated by

all thermal units at time intervalt. If

Phjt Dt







)

set and go to step 14;

otherwise se t.

max

(

ksihjtDtm

PP PP



 



maxt

ksk

PP

P

Step 13: 1mm



 .If

mN, then go to Step 11;

otherwise go to Step 14.

Step 14: 1tt



.IftT



, then go to Step 3; otherwise

go to Step 15.

Step 15: The mo dification process is terminated.

4.6. Selection Based Technique for Handling

Reservoir Storage Volumes Constraints

In this work, the feasibility-based selection rules are

applied to the proposed approach for handling the ine-

quality constraints of reservoir storage volumes con-

straints. The procedures for repairing the reservoir stor-

age volumes constraints are as follows:

Step 1: The overall reservoir storage volumes con-

straints violation of solution

is, which is

defined as



CV x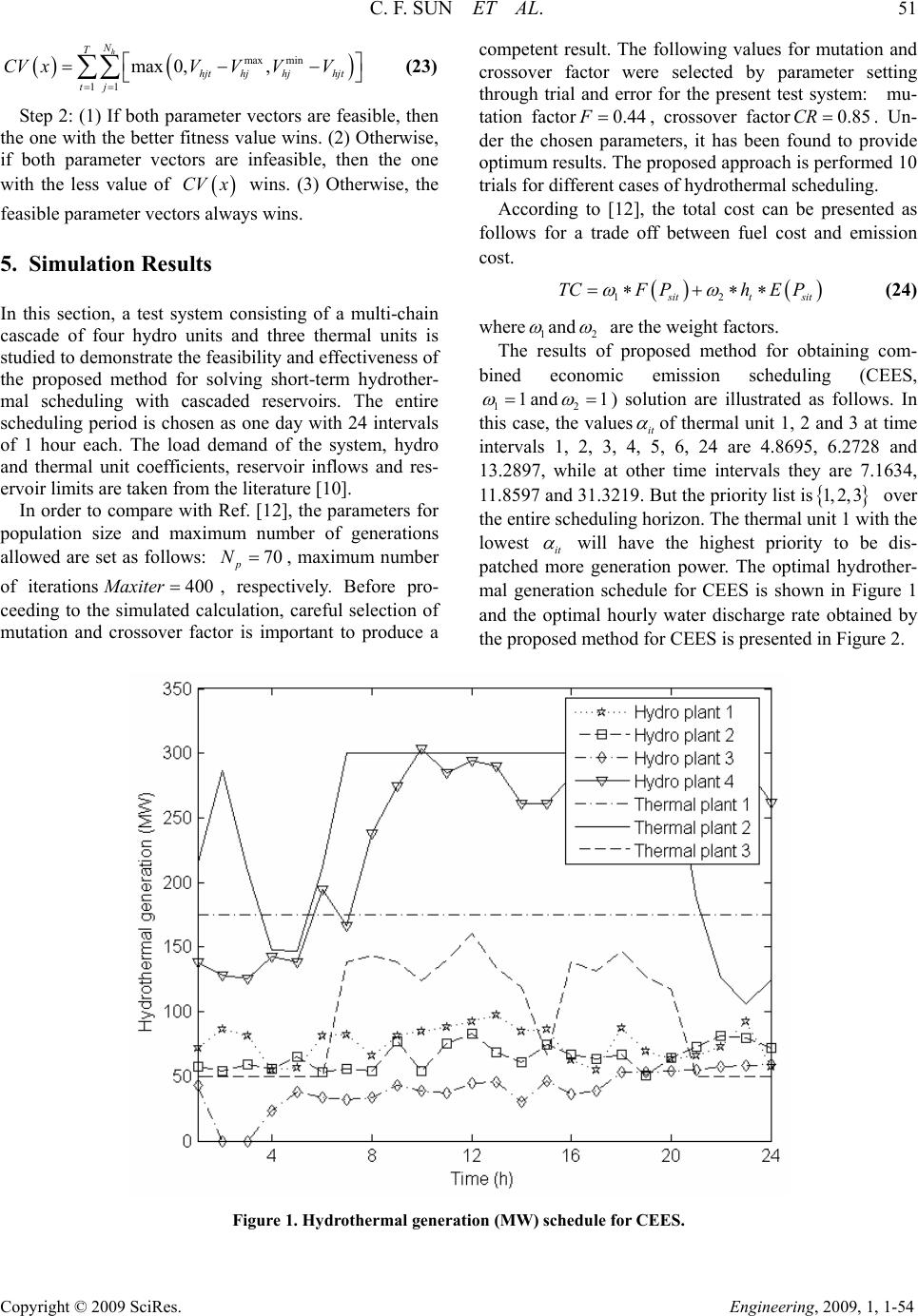

C. F. SUN ET AL. 51









and errot system:





max min

max 0,,

hjt hjhjhjt

CV xVVVV









 (23)

Step 2: (1) If both parameter vectors are feasible, then

the one with the better fitness value wins. (2) Otherwise,

if both parameter vectors are infeasible, then the one

with the less value of wins. (3) Otherwise, the

feasible parameter vectors always wins.



CV x

5. Simulation Results

In this section, a test system consisting of a multi-chain

cascade of four hydro units and three thermal units is

studied to demo ns trate th e feasibility an d effectiveness of

the proposed method for solving short-term hydrother-

mal scheduling with cascaded reservoirs. The entire

scheduling period is chosen as one day with 24 intervals

of 1 hour each. The load demand of the system, hydro

and thermal unit coefficients, reservoir inflows and res-

ervoir limits are taken from the literature [10].

In order to compare with Ref. [12], the parameters for

population size and maximum number of generations

allowed are set as follows: , maximum number

of iterations, respectively. Before pro-

ceeding to the simulated calculation, careful selection of

mutation and crossover factor is important to produce a

competent result. The following values for mutation and

crossover factor were selected by parameter setting

through trial r for the present tes mu-

tation factor0.44F

N

400Maxiter



, crossover factor0.85CR . Un-

der the chosen parameters, it has been found to provide

optimum results. The proposed appr oach is performed 10

tri

s forf between fuel cost ission

cost.

als for different cases of hydrot hermal schedu l i ng.

According to [12], the total cost can be presented as

follow a trade ofand em







it t

TCF PhE



sit

P  (24)

where1



and 2



are the weight factors.

The results of proposed method for obtaining com-

ic emission scheduling (CEES,

bined econom





and 21





) sotion are illustrated as follows. In

this case, the valuesit



of thermal unit 1, 2 and 3 at time

intervals 1, 2, 3, 4, 5, 6, 24 are 4.8695, 6.2728 and

13.2897, while at other time intervals they1634,

11.8597 and 31.3219 . But the pr iority list is



1, 2,3 over

the entire scheduling horizon. The thermal unit 1 with the

lowest it

are 7.



will have the highest priority to be dis-

patched more generation power. The optimal hydrother-

mal generation schedule for CEES is shown in Figure 1

and the optimal hourly water discharge rate obtained by

the proposed method for CEES is presented in Figure 2.

Figure 1. Hydrothermal generation (MW) schedule for CEES.

52 C. F. SUN ET AL.

Figure 2. Hourly hydro plant discharge () for CEES.

Figure 3. Reservoir storage volumes for CEES.

C. F. SUN ET AL. 53

The trajectories of reservoir storage volumes for CEES

are shown in Figure 3. Table 1 shows that using the pro-

posed method optimal fuel cost is found to be $44265.00,

while amount emission is found to be 18060.00 lb.

In Table 1, the optimal solutions of the fuel cost and

emission cost for economic load scheduling (ELS,



and 20



), economic emission scheduling (EES,



and 21t



) and CEES obtained from the pro-

posed approach have been compared with those of DE

[12]. From the results it is quite evident that the proposed

method provides better solutions for short-term com-

bined economic emission hydrothermal scheduling with

cascaded hydro reservoirs. Table 2 presents the best,

worst and mean value of fuel cost and emission of CEES

obtained by differential evolution without priority list,

particle swarm optimization without priority list and the

proposed approach. From the analysis of results in Table 2,

it can be seen that the proposed approach can produce

valuable trade off solutions for CEES. It also shows that

the two objectives of minimizing the fuel cost and emis-

sion cost are of conflicting nature, that is to say, mini-

mizing pollution increases fuel cost and vice versa. From

the results of CEES, it clearly sees that with some com-

promise in fuel cost, it is possible to obtain huge reduc-

tion in emission.

It can be seen clearly from Table 1 that the proposed

method yields much better results in terms of fuel cost,

the amount of emission than known optimization meth-

ods reported in the literature. It is also very important to

note that compared with the results of fuzzy satisfying

[10] the better results from [12] are obtained based on

violating the constraints of the test system, such as the

results of Table 1, Table 3 and Table 5 in Ref. [12], from

which it is clearly shown that the power generation of

thermal unit 1

Pviolates its constraint which

is 1at some time intervals. However, in this

study we obtain even better results while strictly satisfy-

ing all constraints of the test system.

20 175

P

6. Conclusions

In this paper, a novel approach in combination with

novel equality constraint handling techniques has been

successfully introduced to solve hydrothermal scheduling

with non-smooth fuel and emission cost functions. The

major advantages of this novel method are as follows: 1)

In order to handle constraints effectively, heuristic rules

are proposed to handle water dynamic balance con-

straints and heuristic strategies based on priority list are

employed to handle active power balance constraints; 2)

The feasibility-based selection rules are developed to

handle the reservoir storage volumes constraints. Addi-

tionally, the improved heuristic strategies can be simply

incorporated into differential evolution. Hence the pro-

posed method does not require the use of penalty func-

tions and explores the optimum solution at a relatively

lesser computational effort. Numerical experiments show

that the proposed method can obtain better-quality solu-

tions with higher precision than any other optimization

methods reported in the literature. Hence, the proposed

method can well be extended for solving the large-scale

hydrothermal scheduling.

7. Acknowledgements

The authors gratefully acknowledge the financial sup-

ports from National N a tur a l Science Foundation of China

under Grant no. 10876012. The authors thank the

anonymous Reviewers and Editors for constructive and

detailed comments.

Table 1. Comparison of cost for ELS, EES and CEES by

proposed method and DE.

Fuel cost

(

)

Emission

(

)

ELS 42766.0031002.00

EES 46066.0017655.00

The proposed method

CEES 44265.0018060.00

ELS 43500.0021092.00

EES 51449.0018257.00

Differential evolution (DE)

CEES 44914.0019615.00

Table 2. Comparison of cost of CEES by

proposed method, DE and PSO.

Best

Value Worst

ValueMean

Value

Fuel cost($) 44265 4525844622

The proposed

method Emission(lb) 17797 1825518069

Fuel cost($) 47999 4879248390

Differential

evolution without

priority list Emission(lb) 17076 1771617362

Fuel cost($) 45670 4689546530

PSO without

priority list Emission(lb) 16980 1780717295

54 C. F. SUN ET AL.

8. References

[1] J. Tang and B. Peter, “Hydrothermal scheduling via ex-

tended differential dynamic programming and mixed co-

ordination,” IEEE Transactions on Power System, Vol. 10,

pp. 2021-2028 , 1 9 9 5 .

[2] M. Piekutowski, “Optimal short-term scheduling for a

large-scale cascaded hydro system,” IEEE Transactions

on Power System, Vol. 9, pp. 805-811, 1994.

[3] M. V. F. Pereira and L. M. V. G. Pinto, “A decomposition

approach to the economic dispatch of the hydrothermal

systems,” IEEE Transactions on Power Systems, Vol. 101,

pp. 3851-3860 , 1 9 8 2 .

[4] M. Ramirez and P. E. Ontae, “The short-term hydrother-

mal coordination via genetic algorithms,” Electric Power

Components and Systems, Vol. 34, pp. 1-19, 2006.

[5] E. Gil, J. Bustos, and H. Rudnick, “Short-term hydro-

thermal generation scheduling model using a genetic al-

gorithm,” IEEE Transactions on Power System, Vol. 18,

pp. 1256-1264 , 2 0 0 3 .

[6] X. Yuan and Y. Yuan, “A hybrid chaotic genetic algorithm

for short-term hydro system scheduling,” Mathematics

and Computers in Simulation, Vol. 59, pp. 319-327,

2002.

[7] X. Yuan and Y. Yuan, “Application of cultural algorithm

to generation scheduling of hydrothermal systems,” En-

ergy Conversion and Management, Vol. 47, pp. 2192-

2201, 2006.

[8] B. Yu, X. Yuan, and J. Wang, “Short-term hydro-thermal

scheduling using particle swarm optimization method,”

Energy Conversion and Management, Vol. 48, pp. 1902-

1908, 2007.

[9] J. S. Dhillon and D.P. Kothari, “Multi-objective short-

term hydrothermal scheduling based on heuristic search

technique,” Asian Journal of Information Technology, Vol.

6, pp. 447-454, 2007.

[10] M. Basu, “An interactive fuzzy satisfying method based

on evolutionary programming technique for multi-objec-

tive short-term hydrothermal scheduling,” Electric Power

Systems Research, Vol. 69, pp. 277-285, 2004.

[11] J. S. Dhillon, S. C. Parti, and D. P. Kothari, “Fuzzy deci-

sion-making in stochastic multi-objective short-term

hydrothermal scheduling,” IEE Proceedings of Genera-

tion Transmission and Distribution, Vol. 149, pp.

191-200, 2002.

[12] K. K. Mandal and N. Chakraborty, “Short-term combined

economic emission scheduling of hydrothermal power

systems with cascaded reservoirs using differential evolu-

tion,” Energy Conversion and Management, Vol. 50, pp.

97-104, 2009.

[13] R. Storn and K. Price, “Differential evolution–a simple

and efficient heuristic for global optimization over con-

tinuous spaces,” Journal of Global Optimization, Vol. 11,

pp. 341-359, 1997.

[14] X. H. Yuan, L. Wang, Y. C. Zhang, and Y. B. Yuan, “A

hybrid differential evolution method for dynamic eco-

nomic dispatch with valve-point effects,” Expert System

with Application, Vol. 36, pp. 4042-4048, 2009.

[15] X. H. Yuan, B. Cao, B. Yang, and Y. B. Yuan. “Hydro-

thermal scheduling using chaotic hybrid differential evo-

lution”, Energy Conversion and Management, Vol. 49, pp.

3627-3633, 2008.

[16] S. K. Wang, J. P. Chiou, and C. W. Liu, “Non-smooth/

non-convex economic dispatch by a novel hybrid differ-

ential evolution algorithm,” IEE Proceeding Generation

Transmission and Distribution, Vol. 1, pp. 793-803, 2007.

[17] C. F. Changa, J. J. Wong, J. P. Chiou, and C. T. Su, “Ro-

bust searching hybrid differential evolution method for

optimal reactive power planning in large-scale distribu-

tion sytems,” Electric Power Systems Research, Vol. 77,

pp. 430-437, 2007.

[18] J. P. Chiou, “Variable scaling hybrid differential evolution

for large-scale economic dispatch problems,” Electric

Power Systems Research, Vol. 77, pp. 212-2 1 8, 2007.