Engineering, 2009, 1, 1-54
Published Online June 2009 in SciRes (http://www.SciRP.org/journal/eng/).
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
Skyhook Surface Sliding Mode Control on Semi-Active Vehicle
Suspension System for Ride Comfort Enhancement
Yi Chen*
Department of Mechanical Engineering, University of Glasgow, Glasgow, United Kingdom
Received March 25, 2009; revised April 11, 2009; accepted April 18, 2009
Abstract
A skyhook surface sliding mode control method was proposed and applied to the control on the semi-active
vehicle suspension system for its ride comfort enhancement. A two degree of freedom dynamic model of a
vehicle semi-active suspension system was given, which focused on the passenger’s ride comfort perform-
ance. A simulation with the given initial conditions has been devised in MATLAB/SIMULINK. The simula-
tion results were showing that there was an enhanced level of ride comfort for the vehicle semi-active sus-
pension system with the skyhook surface sliding mode controller.
Keywords: Sliding Mode Control, Skyhook Damper, Fuzzy Logic Control, Semi-Active Suspension System
1. Introduction
The ride comfort is one of the most important character-
istics for a vehicle suspension system. By reducing the
vibration transmission and keeping proper tire contacts,
the active and semi-active suspension system are de-
signed and developed to achieve better ride comfort per-
formance than the passive suspension system. The active
suspension is designed to use separate actuators which
can exert an independent force on the suspension, this
action is to improve the suspension ride comfort per-
formance. The active suspension system has been inves-
tigated since 1930s, but for the bottle neck of complex
and high cost for its hardware, it has been hard for a
wide practical usage and it is only available on premium
luxury vehicle [1]. Semi-active (SA) suspension system
was introduced in the early 1970s, it has been considered
as good alternative between active and passive suspen-
sion system. The conceptual idea of SA suspension is to
replace active force actuators with continually adjustable
elements, which can vary or shift the rate of the energy
dissipation in response to instantaneous condition of mo-
tion. SA suspension system can only change the viscous
damping coefficient of the shock absorber, it will not add
additional energy to the suspension system. The SA sus-
pension system is also less expensive and energy cost
than active suspension system in operation [2]. In recent
years, research on SA suspension system has been con-
tinuing to advance with respect to their capabilities, nar-
rowing the gap between SA and active suspension sys-
tem. SA suspension system can achieve the majority of
the performance characteristics of active suspension sys-
tem, which cause a wide class of practical applications.
Magnetorheological / Electrorheological (MR/ER) [3
-5] dampers are both of the most widely studied and
tested components of the SA suspension system. MR/ER
fluids are materials that respond to an applied mag-
netic/electrical field with a change in rheological behav-
iour.
Variable structure control (VSC) with sliding mode
control was introduced in the early 1950s by Emelyanov
and was published in 1960s [6], further work was devel-
oped by several researchers [7-9]. Sliding mode control
(SMC) has been recognized as a robust and efficient
control method for complex high order nonlinear dy-
namical system. The major advantage of sliding mode
control is the low sensitivity to a system's parameter
changing under various uncertainty conditions, and it can
decouple system motion into independent partial com-
*Yi Chen is with the Department of Mechanical Engineering, Univer-
sity of Glasgow, Glasgow, United Kingdom, G12 8QQ. Tel:
44(0)-141-330-2477, Fax: [phone].

24 Y. CHEN
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
ponents of lower dimension, which reduces the complex-
ity of the system control and feedback design. A major
drawback of traditional SMC is chattering, which is gen-
erally disadvantageous within control system.
In recent years, a lot of literature has been generated in
the area of SMC and has covered the improvement for
traditional SMC, they harnessed to achieve better per-
formance and reduce the chattering problem. A skyhook
surface sliding mode control (SkyhookSMC) method
will be developed and applied to the semi-active vehicle
suspension system for the ride comfort enhancement in
this paper.
It has been also well recognized, fuzzy logic control
(FLC) is effective and robust control method for various
applications, the FLC’s rule-base comes from human's
practical experience, however, the linguistic expression
of the FLC rule-base makes it difficult to make guarantee
the stability and robustness of the control system [10-11].
In order to compare and validate the control effects from
the SkyhookSMC, a FLC controller is also designed in
this paper.
2. Two Degree of Freedom Semi-Active
Suspension System
The role of the vehicle suspension system is to support
and isolate the vehicle body and payload from road dis-
turbances, maintain the traction force between tires and
road surface. The SA suspension system can offer both
the reliability and versatility including passenger ride
comfort with less power demand.
A two degree of freedom model which focused on the
passenger ride comfort performance is proposed for SA
suspension system in Figure 1. The SA suspension model
can be defined by the Equation (1), where, m1 and m2 are
the unsprung mass and the sprung mass respectively, k1
is tire deflection stiffness, k2 and c2 are suspension stiff-
ness and damping coefficients respectively, ce is the
semi-active damping coefficient which can generate
damping force of fd by MR/ER absorber in Equation (2).
z1, z2 and q are the displacements for unsprung mass,
sprung mass and road disturbance respectively, g is the
acceleration of gravity. In order to observe the SA sus-
pension status, the Equation (1) is re-written as a
state-space in Equation (3).
(1)
(2)
(3)
In Equation (3), X is the state matrix for 2-DOF SA
suspension system, which including tire deformation,
suspension deformation, unsprung mass velocity and
sprung mass velocity. Y is the output matrix, which in-
cluding vehicle body acceleration, tire deformation, sus-
pension deformation. U is the control force matrix. Q is
the external disturbance matrix, which contains two dis-
turbance signals: road profile of velocity and gravity
acceleration for 2-DOF SA suspension system modelling.
A, B, C, D, E, F are coefficient matrixes.
3. Sliding Mode Control with Skyhook
Surface Design
In designing a SkyhookSMC, the objective is to consider
Figure 1. Two degree of freedom semi-active suspension
system.

Y. CHEN 25
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
the non-linear tether system as the controlled plant, and
therefore defined by the general state-space in Equation
(4), where x
∈ Rn is the state vector, n is the order of the
non-linear system, and u ∈ Rm is the input vector, m is
the number of inputs.
(4)
s(e,t) is the sliding surface of the hyper-plane, which is
given in Equation (5) and shown in Figure 2, where λ is
a positive constant that defines the slope of the sliding
surface.
(5)
In the 2-DOF SA suspension system, we let n = 2,
given that, as it is a second-order system in which s de-
fines the position and velocity errors.
(6)
From Equations (5) and (6), the second-order tracking
problem is now being replaced by a first-order stabiliza-
tion problem in which the scalar s is kept at zero by
means of a governing condition [12]. This is obtained
from use of the Lyapunov stability theorem, given in
Equation (7), and it states that the origin is a globally
asymptotically stable equilibrium point for the control
system. Equation (7) is positive definite and its time de-
rivative is given in inequality (8), to satisfy the negative
definite condition, the system should satisfy the inequal-
ity in (8).
(7)
(8)
The ideal Skyhook control strategy was introduced in
1974 by Karnopp et al. [13], which is known as one of
the most effective in terms of the simplicity of the con-
trol algorithm. Figure 3 gives the ideal skyhook control
scheme, the basic idea is to link the vehicle body sprung
Figure 2. Sliding surface design.
mass to the stationary sky by a controllable ‘skyhook’
damper, which could generate the controllable force of
fskyhook and reduce the vertical vibrations by the road dis-
turbance of all kinds [14-15]. Their original work uses
only one inertia damper between the sprung mass and the
inertia frame. The skyhook control is applicable for both
a semi-active system as well as an active system. In
practical, the skyhook control law was designed to
modulate the damping force by a passive device to ap-
proximate the force that would be generated by a damper
fixed to an inertial reference as the ‘sky’.
The skyhook control can reduce the resonant peak of
the sprung mass quite significantly and thus can achieve
a good ride quality. By borrowing this idea to reduce the
sliding chattering phenomenon, in Figure 4, a soft switch-
ing control law is introduced for the major sliding sur-
face switching activity in Equation (9), which is to
achieve good switch quality for the SkyhookSMC. The
variable of s is defined in Equation (6), which contains
the system information. It can be taken as a part of the
SkyhookSMC control law in Equation (9), where c0 is an
Figure 3. Ideal Skyhook control scheme.
Figure 4. Sliding mode surface design with skyhook con-
trol law.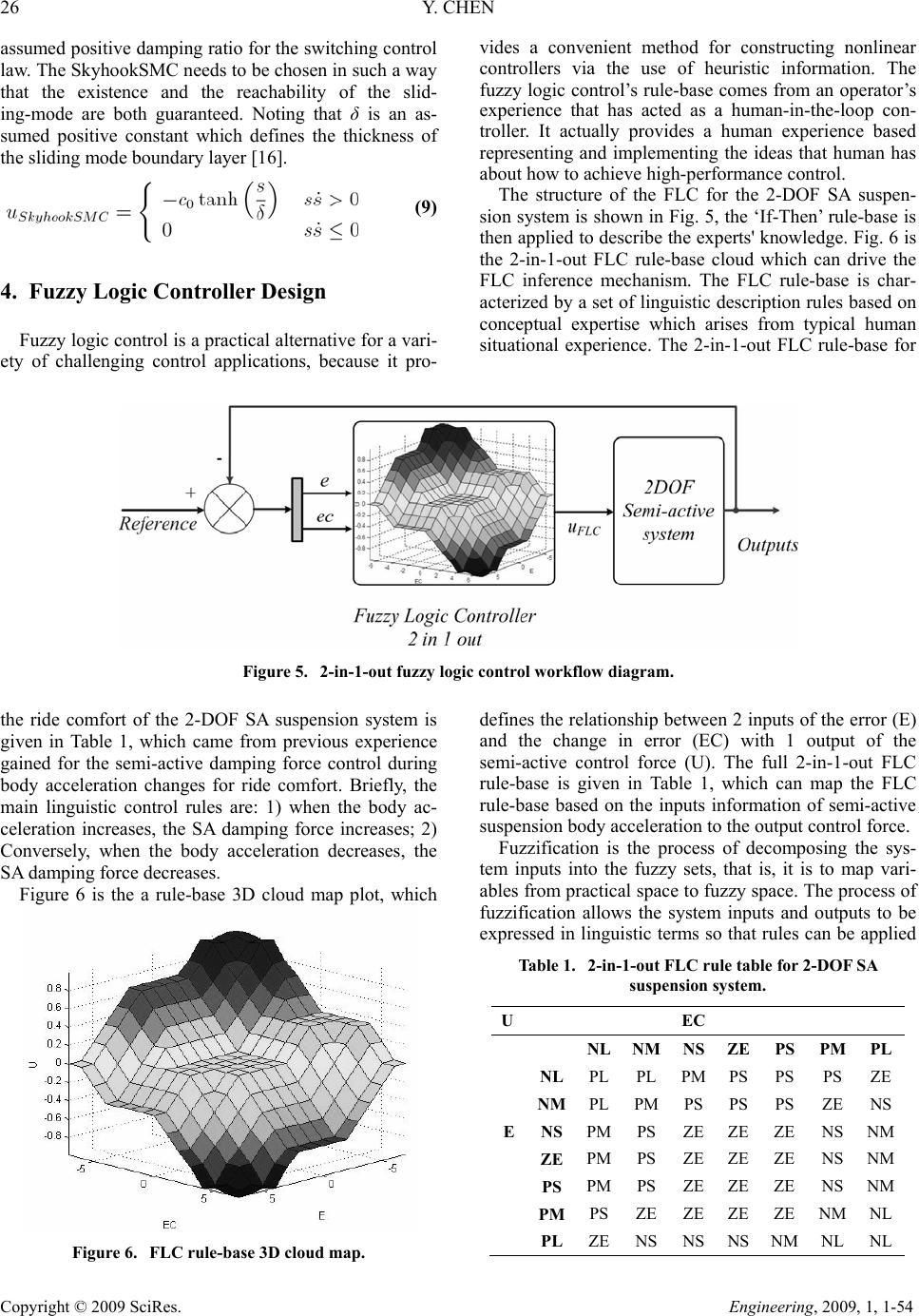

26 Y. CHEN
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
assumed positive damping ratio for the switching control
law. The SkyhookSMC needs to be chosen in such a way
that the existence and the reachability of the slid-
ing-mode are both guaranteed. Noting that δ is an as-
sumed positive constant which defines the thickness of
the sliding mode boundary layer [16].
(9)
4. Fuzzy Logic Controller Design
Fuzzy logic control is a practical alternative for a vari-
ety of challenging control applications, because it pro-
vides a convenient method for constructing nonlinear
controllers via the use of heuristic information. The
fuzzy logic control’s rule-base comes from an operator’s
experience that has acted as a human-in-the-loop con-
troller. It actually provides a human experience based
representing and implementing the ideas that human has
about how to achieve high-performance control.
The structure of the FLC for the 2-DOF SA suspen-
sion system is shown in Fig. 5, the ‘If-Then’ rule-base is
then applied to describe the experts' knowledge. Fig. 6 is
the 2-in-1-out FLC rule-base cloud which can drive the
FLC inference mechanism. The FLC rule-base is char-
acterized by a set of linguistic description rules based on
conceptual expertise which arises from typical human
situational experience. The 2-in-1-out FLC rule-base for
Figure 5. 2-in-1-out fuzzy logic control workflow diagram.
defines the relationship between 2 inputs of the error (E)
and the change in error (EC) with 1 output of the
semi-active control force (U). The full 2-in-1-out FLC
rule-base is given in Table 1, which can map the FLC
rule-base based on the inputs information of semi-active
suspension body acceleration to the output control force.
the ride comfort of the 2-DOF SA suspension system is
given in Table 1, which came from previous experience
gained for the semi-active damping force control during
body acceleration changes for ride comfort. Briefly, the
main linguistic control rules are: 1) when the body ac-
celeration increases, the SA damping force increases; 2)
Conversely, when the body acceleration decreases, the
SA damping force decreases.
Fuzzification is the process of decomposing the sys-
tem inputs into the fuzzy sets, that is, it is to map vari-
ables from practical space to fuzzy space. The process of
fuzzification allows the system inputs and outputs to be
expressed in linguistic terms so that rules can be applied
Figure 6 is the a rule-base 3D cloud map plot, which
Table 1. 2-in-1-out FLC rule table for 2-DOF SA
suspension system.
U EC
NLNMNS ZE PS PMPL
NL PLPLPM PS PS PSZE
NM PLPM PS PS PS ZENS
ENSPMPSZE ZE ZE NS NM
ZE PMPSZE ZE ZE NSNM
PS PMPSZE ZE ZE NSNM
PM PSZEZE ZE ZE NMNL
PL ZENSNS NS NM NLNL
Figure 6. FLC rule-base 3D cloud map.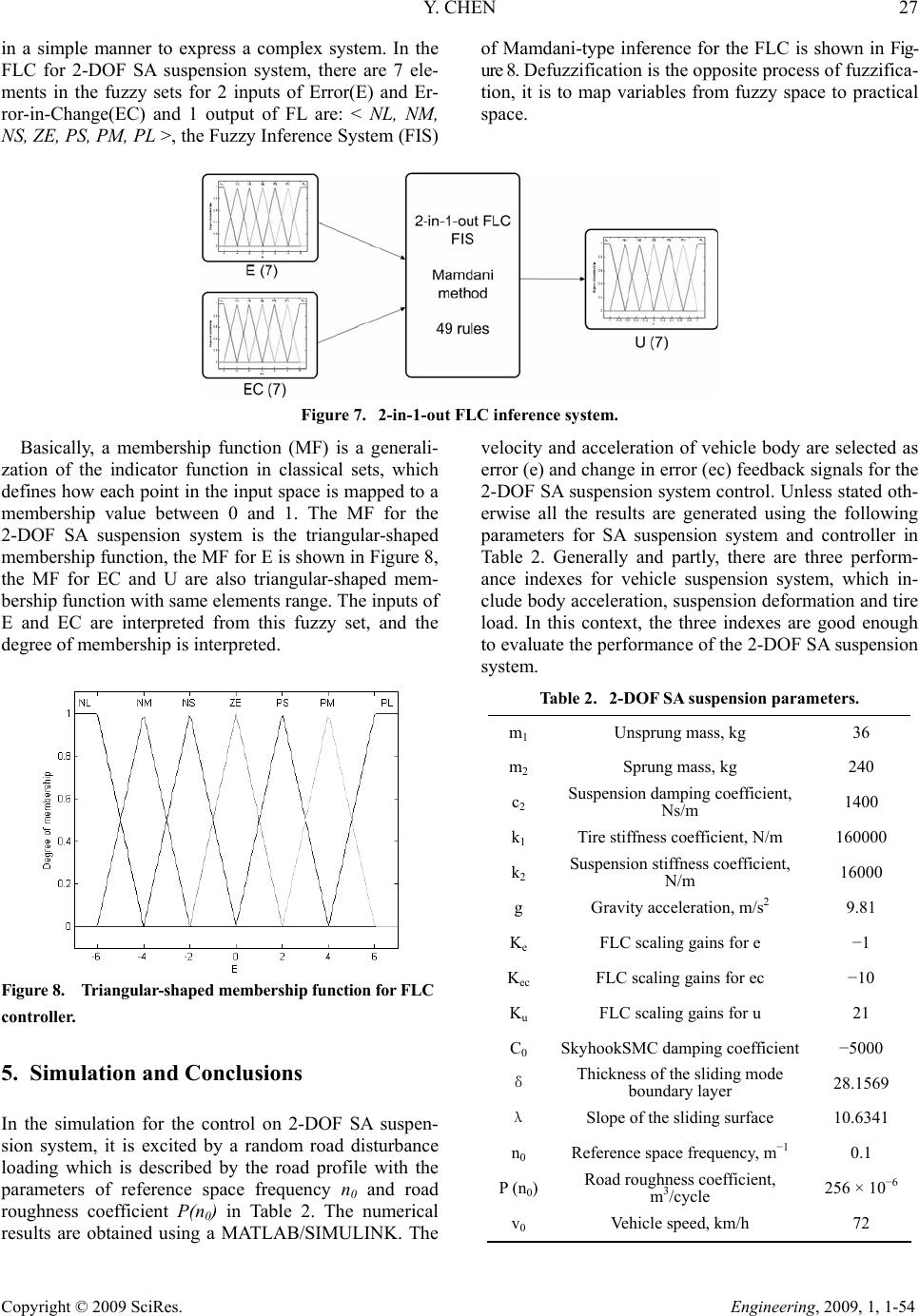

Y. CHEN 27
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
in a simple manner to express a complex system. In the
FLC for 2-DOF SA suspension system, there are 7 ele-
ments in the fuzzy sets for 2 inputs of Error(E) and Er-
ror-in-Change(EC) and 1 output of FL are: < NL, NM,
NS, ZE, PS, PM, PL >, the Fuzzy Inference System (FIS)
of Mamdani-type inference for the FLC is shown in Fig-
ure 8. Defuzzification is the opposite process of fuzzifica-
tion, it is to map variables from fuzzy space to practical
space.
Figure 7. 2-in-1-out FLC inference system.
Basically, a membership function (MF) is a generali-
zation of the indicator function in classical sets, which
defines how each point in the input space is mapped to a
membership value between 0 and 1. The MF for the
2-DOF SA suspension system is the triangular-shaped
membership function, the MF for E is shown in Figure 8,
the MF for EC and U are also triangular-shaped mem-
bership function with same elements range. The inputs of
E and EC are interpreted from this fuzzy set, and the
degree of membership is interpreted.
Figure 8. Tr iangular -shaped membership function for FLC
controller.
5. Simulation and Conclusions
In the simulation for the control on 2-DOF SA suspen-
sion system, it is excited by a random road disturbance
loading which is described by the road profile with the
parameters of reference space frequency n0 and road
roughness coefficient P(n 0) in Table 2. The numerical
esults are obtained using a MATLAB/SIMULINK. The
velocity and acceleration of vehicle body are selected as
error (e) and change in error (ec) feedback signals for the
2-DOF SA suspension system control. Unless stated oth-
erwise all the results are generated using the following
parameters for SA suspension system and controller in
Table 2. Generally and partly, there are three perform-
ance indexes for vehicle suspension system, which in-
clude body acceleration, suspension deformation and tire
load. In this context, the three indexes are good enough
to evaluate the performance of the 2-DOF SA suspension
system.
r
Table 2. 2-DOF SA suspension parameters.
m1 Unsprung mass, kg 36
m2 Sprung mass, kg 240
c2 Suspension damping coefficient,
Ns/m 1400
k1 Tire stiffness coefficient, N/m 160000
k2 Suspension stiffness coefficient,
N/m 16000
g Gravity acceleration, m/s2 9.81
Ke FLC scaling gains for e −1
Kec FLC scaling gains for ec −10
Ku FLC scaling gains for u 21
C0 SkyhookSMC damping coefficient −5000
δ Thickness of the sliding mode
boundary layer 28.1569
λ Slope of the sliding surface 10.6341
n0 Reference space frequency, m−1 0.1
P (n0)Road roughness coefficient,
m3/cycle 256 × 10−6
v0 Vehicle speed, km/h 72

28 Y. CHEN
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
Figure 9. MATLAB/SIMULINK block for 2-DOF SA suspension system.
Figure 9 is the SkyhookSMC and FLC MAT-
LAB/SIMULINK block for 2-DOF SA suspension sys-
tem, which can compare the ride comfort performance
with both SkyhookSMC and FLC control methods, all
the post-simulation data analysis and plots are also gen-
erated by this SIMULINK block and its support MAT-
LAB functions.
Mostly, a road profile is a series of random data in the
actual surroundings. That is reason to describe the road
profile by statistical techniques. One practical statistical
way to generate road input is describing the road rough-
ness in power spectral density (PSD). To generate the
road profile of a random base excitation for the 2-DOF
SA suspension simulation disturbance, a spectrum of the
geometrical road profile with road class roughness-C is
considered. The vehicle is travelling with a constant
speed v0, the time histories data of road irregularity are
described by PSD method [17-19]. According to Inter-
national Standard Organization (ISO)2631 [20], the ride
comfort is specified in terms of root mean square (RMS)
acceleration over a frequency range, in this simulation
the RMS values for SkyhookSMC and FLC are {1.0530,
1.3134}, respectively, which confirms the validation of
the SkyhookSMC on the ride comfort enhancement for
2-DOF SA suspension system.
The FLC parameters require a judicious choice of the
scaling gains of {Ke, Kec} for fuzzification and the scal-
ing gain of {Ku} for defuzzification, in which, the {Ku} is
used to map the control force from the fuzzy space range
to practical space range that actuators can work practi-
cally. Similarly, the SkyhookSMC damping coefficient c0
is required to expand the normalised controller output
force into a practical range. The thickness of the sliding
mode boundary layer is given by δ = 28.1569, and the
slope of the sliding surface λ = 10.6341. Both of δ and λ
value came from previous passive 2-DOF SA suspension
system simulation results without control. With different
simulation results of SkyhookSMC and FLC for the
2-DOF SA suspension system, all the control methods
have an effect on the ride comfort enhancement for the
2-DOF suspension system in the given initial conditions.
Figure 10 gives the vertical behaviour of body accel-
eration - ride comfort performance. The upper subplot in
Fig. 10 contains the body acceleration plots for SA sus-
pension with FLC and passive suspension system, the
FLC has body acceleration reducing effects on the pas-
sive suspension system to some extend, which depends
on the human experience in FLC’s rule-base. Meanwhile,
the lower subplot in Figure 10 compares the control ef-
fects of SkyhookSMC and FLC control methods, it
shows SkyhookSMC has better control effect than the
FLC on body acceleration reducing.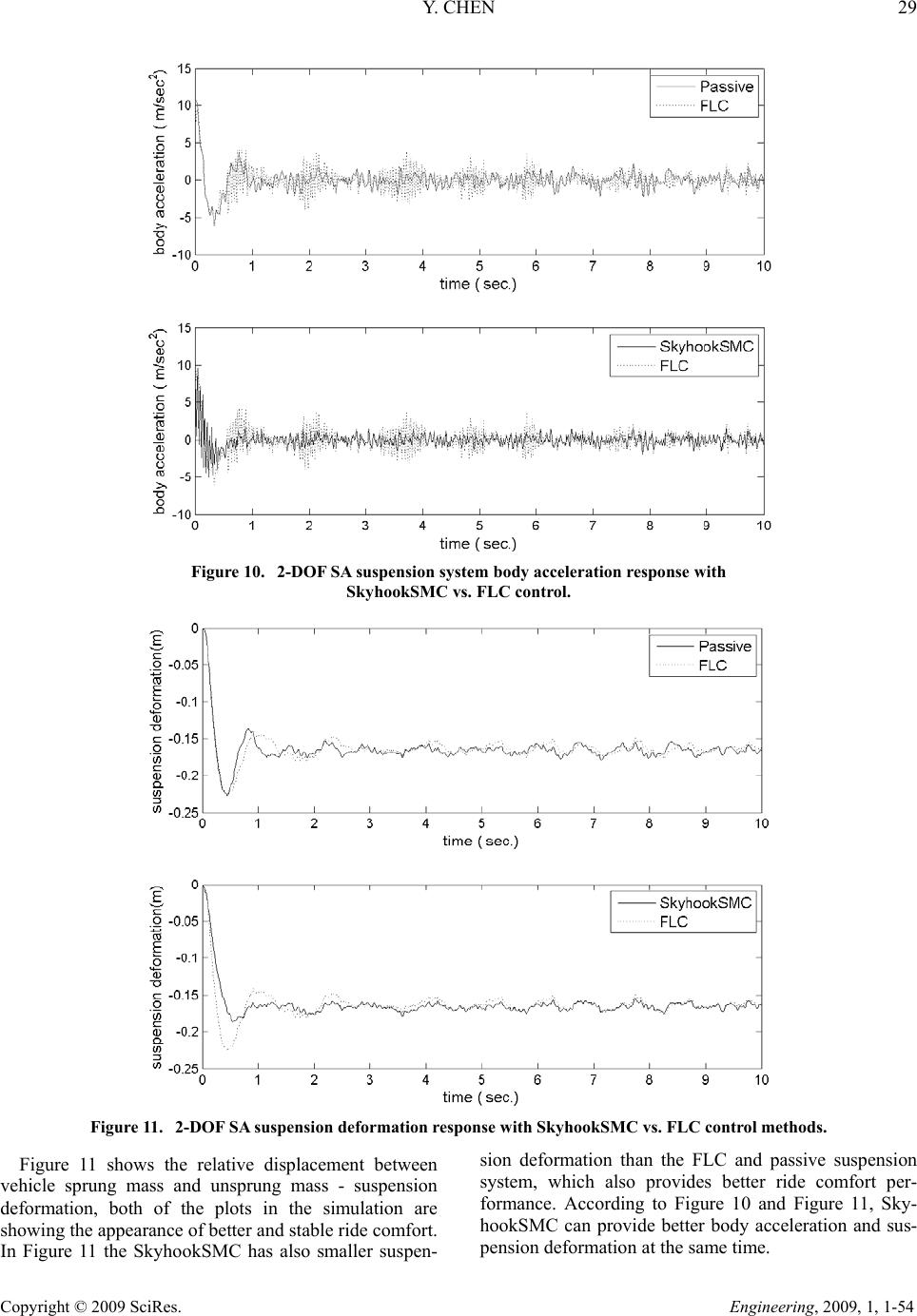

Y. CHEN 29
C opyright © 2009 SciRes. Engineering, 2009, 1, 1-54
Figure 10. 2-DOF SA suspension system body acceleration response with
SkyhookSMC vs. FLC control.
Figure 11. 2-DOF SA suspension deformation response with SkyhookSMC vs. FLC control methods.
Figure 11 shows the relative displacement between
vehicle sprung mass and unsprung mass - suspension
deformation, both of the plots in the simulation are
showing the appearance of better and stable ride comfort.
In Figure 11 the SkyhookSMC has also smaller suspen-
sion deformation than the FLC and passive suspension
system, which also provides better ride comfort per-
formance. According to Figure 10 and Figure 11, Sky-
hookSMC can provide better body acceleration and sus-
pension deformation at the same time.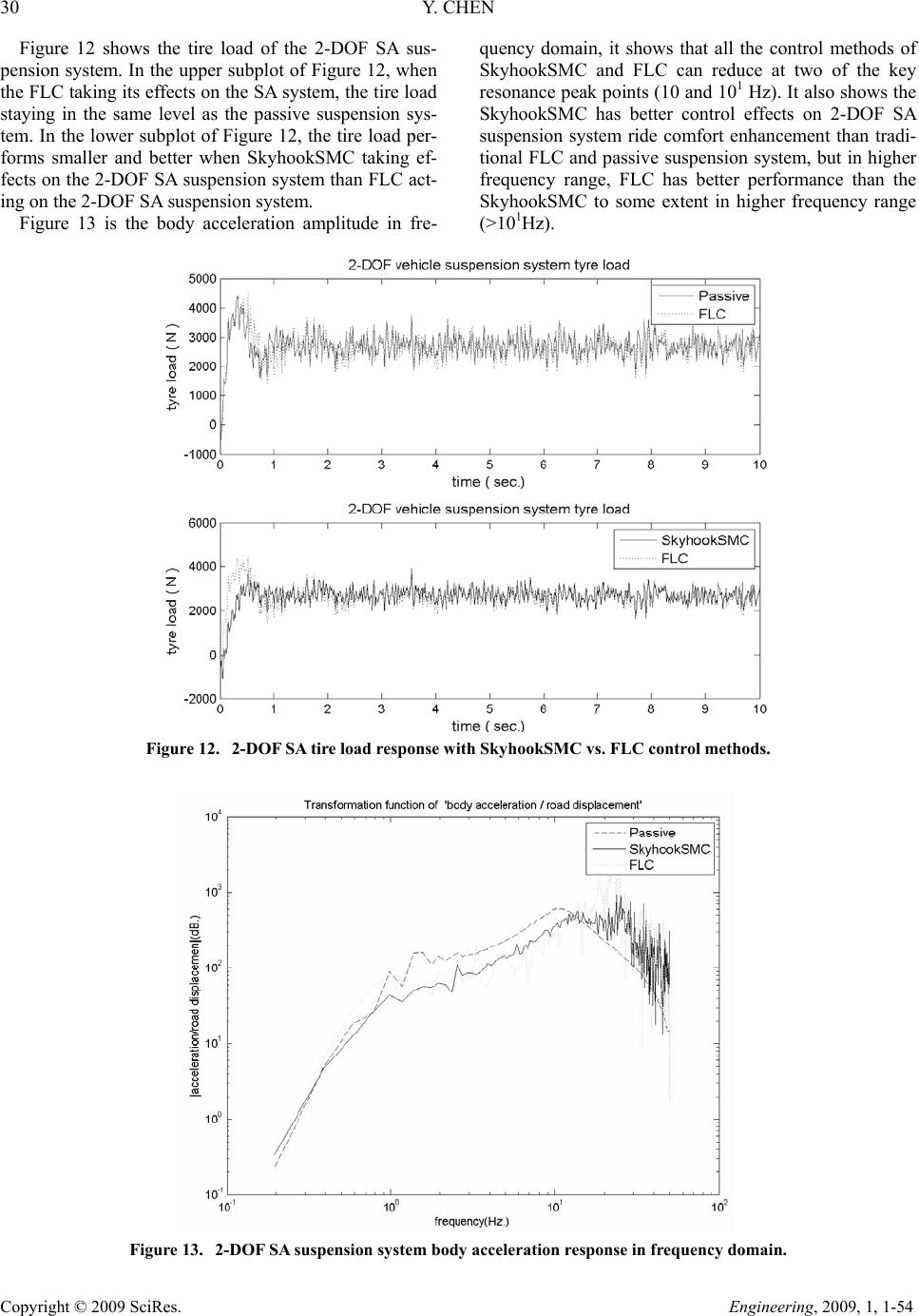

30 Y. CHEN
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
Figure 12 shows the tire load of the 2-DOF SA sus-
pension system. In the upper subplot of Figure 12, when
the FLC taking its effects on the SA system, the tire load
staying in the same level as the passive suspension sys-
tem. In the lower subplot of Figure 12, the tire load per-
forms smaller and better when SkyhookSMC taking ef-
fects on the 2-DOF SA suspension system than FLC act-
ing on the 2-DOF SA suspension system.
Figure 13 is the body acceleration amplitude in fre-
quency domain, it shows that all the control methods of
SkyhookSMC and FLC can reduce at two of the key
resonance peak points (10 and 101 Hz). It also shows the
SkyhookSMC has better control effects on 2-DOF SA
suspension system ride comfort enhancement than tradi-
tional FLC and passive suspension system, but in higher
frequency range, FLC has better performance than the
SkyhookSMC to some extent in higher frequency range
(>101Hz).
Figure 12. 2-DOF SA tire load response with SkyhookSMC vs. FLC control methods.
Figure 13. 2-DOF SA suspension system body acceleration response in frequency domain.

Y. CHEN 31
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
Figure 14. 2-DOF SA suspension system body response phase plot.
Figure 15. Sliding surface switching plot.
The phase plot (body velocity vs. body acceleration) is
shown in Figure 14 as limit cycles with behaviour for
2-DOF SA suspension body vertical vibration, the curves
started from the initial value point of (0,g), and gathered
to the stable points area around (0,0) in close-wise direc-
tion, clearly, SkyhookSMC controller goes faster from
the start point to steady status point, which corroborated
the 2-DOF SA suspension system’s SkyhookSMC con-
trollable steady-state.
6. Future Work
The further study on the FLC and SkyhookSMC control
methods by experimental system for the 2-DOF SA sus-
pension system need to be designed. The further control
methods will be studied to balance the control ability of
FLC and SkyhookSMC to make obvious enhancement
for the 2-DOF SA suspension system ride comfort in
both time and frequency domain.

32 Y. CHEN
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
The parameter settings for the FLC and SkyhookSMC,
including the SkyhookSMC damping coefficient c0,
thickness of the sliding mode boundary layer δ, slope of
the sliding surface λ and FLC scaling gains of {Ke, Kec,
Ku}, need further consideration because the current
simulation results come from manual parameter selection
which based on passive suspension system simulation
results. In order to enhance the parameter selection proc-
ess and validation, some computational intelligence (CI)
optimisation tools, such as Genetic Algorithms (GA) and
Artificial Neural Networks (ANN), could be applied for
parameter selection for the FLC and SkyhookSMC, this
can hopefully give some reference sets for parameter
selection. A GA has been used as an optimisation tool for
parameter selection of the motorised momentum ex-
change tether system payload transfer from low Earth
orbit to geostationary Earth orbit, and the GA’s optimisa-
tion ability has therefore been reasonably demonstrated
[21].
7. Acknowledgements
The author would like to acknowledge the support pro-
vided by the Overseas Research Students Awards
Scheme and the Scholarship awarded by the University
of Glasgow’s Faculty of Engineering.
8. References
[1] K. Yi, M. Wargelin, and K. Hedrick, “Dynamic tire force
control by semiactive suspensions,” Journal of Dynamic
Systems, Measurement, and Control, Vol. 115, No. 3, pp.
465-474, 1993.
[2] N. Jalili, “A comparative study and analysis of
semi-active vibration-control systems,” Journal of Vibra-
tion and Acoustics, Vol. 124, No. 4, pp. 593-605, 2002.
[3] R. Stanway, “The development of force actuators using
ER and MR fluid technology,” Actuator Technology:
Current Practice and New Developments, IEE Collo-
quium on (Digest No: 1996/110), Vol. 6, pp. 1-5, 1996.
[4] L. Caracoglia and N. P. Jones, “Passive hybrid technique
for the vibration mitigation of systems of interconnected
stays,” Journal of Sound and Vibration, Vol. 307, No. 3-5,
pp. 849-864, 2007.
[5] Q. Zhou, S. R. K. Nielsen, and W. L. Qu, “Semi-active
control of shallow cables with magnetorheological
dampers under harmonic axial support motion,” Journal
of Sound and Vibration, Vol. 311, No. 3-5, pp. 683-706,
2008.
[6] S. V. Emelyanov, “Variable structure control systems (in
Russian),” Moscow: Nauka, 1967.
[7] Y. Itkis, “Control systems of variable structure,” New
York: Wiley, 1976.
[8] V. A. Utkin, “Sliding modes and their application in vari-
able structure systems,” Moscow: Nauka (in Russian),
1978.
[9] J. Y. Hung, W. Gao, and J. C. Hung, “Variable structure
control: A survey,” IEEE Transactions on Industrial Elec-
tronics, pp. 2-22, 1993.
[10] L. A. Zadeh, “Fuzzy sets,” Information and Control, Vol.
8, No. 3, pp. 338–353, 1965.
[11] K. M. Passino and S. Yurkovich, “Fuzzy control,” Addi-
son Wesley Longman, Menlo Park, CA, 1998.
[12] J. J. E. Slotine and W. P. Li, “Applied nonlinear control,”
Prentice-Hall International, 1991.
[13] D. C. Karnopp, M. J. Crosby, and R. A. Harwood, “Vi-
bration control using semi-active force generators,”
Journals of Engineering for Industry, Transactions of the
ASME, Vol. 94, pp. 619-626, 1974.
[14] H.-S. Kima and P. N. Roschke, “Design of fuzzy logic
controller for smart base isolation system using genetic
algorithm,” Engineering Structures, Vol. 28, No. 1, pp.
84-96, 2006.
[15] S. M. Savaresi, E. Silani, and S. Bittanti, “Accelera-
tion-Driven-Damper (ADD): An optimal control algo-
rithm for comfort-oriented semiactive suspensions,”
ASME Transactions: Journal of Dynamic Systems,
Measurement and Control, Vol. 127, No. 2, pp. 218-229,
2005.
[16] J. J. E. Slotine, “Tracking control of non-linear systems
using sliding surfaces with application to robot manipula-
tions,” PhD Dissertation, Laboratory for Information and
Decision Systems, Massachusetts Institute of Technology,
1982.
[17] E. M. Elbeheiry and D. C. Karnopp, “Optimal control of
vehicle random vibration with constrained suspension
deflection,” Journal of Sound and Vibration, Vol. 189, No.
5, pp. 547-564, 1996.
[18] Y. Liu, H. Matsuhisaa, and H. Utsunoa, “Semi-active
vibration isolation system with variable stiffness and
damping control,” Journal of Sound and Vibration, Vol.
313, No. 1-2, pp. 16-28, 2008.
[19] K. Ramji, A. Gupta, V. H. Saran, V. K. Goel, and V.
Kumar, “Road roughness measurements using PSD ap-
proach,” Journal of the Institution of Engineers, Vol. 85,
pp. 193-201, 2004.
[20] International Organization for Standardization, “Me-
chanical vibration and shock – evaluation of human ex-
posure to whole-body vibration – Part 1: General re-
quirements,” ISO 2631-1, 1997.
[21] Y. Chen and M. P. Cartmell, “Multi-objective optimisa-
tion on motorised momentum exchange tether for pay-
load orbital transfer,” IEEE Congress on Evolutionary
Computation, pp. 987-993, September 25-28, 2007.