Engineering, 2009, 1, 1-54
Published Online June 2009 in SciRes (http://www.SciRP.org/journal/eng/).
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
An Identified Study on the Active Network of
a Thermoacoustic Regenerator
Guozhong Ding1, Feng Wu2, Gang Zhou3, Xiaoqin g Z ha ng1, Jiuyang Yu2
1School of Energy and Power Engineering, State key laboratory of coal combustion,
Huazhong University of Science and Technology, Wuhan, Hubei, China
2School of Science, Wuhan Institute of Technology, Wuha n, China
3Technical Institute of Physics and Chemistry, Chinese Academy of Science, Beijing, China
Received March 27, 2009; revised April 30, 2009; accepted May 4, 2009
Abstract
An active thermo-acoustic network model of regenerator which is a key component to accomplish the con-
version between thermal-and acoustic power in thermo-acoustic system has been established in this paper.
The experiment was carried out to quantify the network. A method called least square is employed in order to
identify the H matrix describing the system. The results obtained here show that the active thermo-acoustic
network can reliably depict the characteristics of a thermo-acoustic system.
Keywords: Regenerator, Active Network, H Matrix, System Identification
1. Introduction
The regenerator, which produces thermo-acoustic effects,
is a key component for thermo-acoustic engines (refrig-
erators), and its performance has a significant impact on
engine system. In recent years research on regenerators
has received significant attention due to the complexity
of oscillating flow. Gary et al. developed a computa-
tional model for a regenerator based upon the bounded
derivative method by Kreiss [1]. Y. Matsubara studied
the effect of void volume in regenerator [2]. Kwanwoo et
al. made use of a novel flow analysis method for regen-
erator under oscillating flow [3] and Chen et al. studied
the heat transfer characteristics of oscillating flow re-
generator [4]. While their method produces accurate re-
sults, the implementation is difficult. Swift [5] showed
that regenerators can convert heat into acoustic work,
and a regenerator with longitude temperature gradient is
an active network. The regenerator network model [6],
which is based on linear thermo-acoustic theory, was
adopted for theoretical analysis and engineering calcula-
tion.
The system identification is a powerful tool for
investigation of practical engineering devices. By means
of fitting experimental data, model parameters can be
found and applied to the model for use in engineering.
The objective of this paper is to identify these parameters
of the thermo-acoustic network describing the regenera-
tor in a thermo-acoustic engine. An active network
model of regenerator has been established by solving
transport equations describing the regenerator used in
this paper. By adopting capillary numbers as identifica-
tion parameter, the transport matrix of the network is
identified systematically, this includes effects of the re-
sistance and compliance to avoid linear error of the
model. The results obtained herein will be useful for
quantifying the network describing the regenerators and
for the optimal design of real regenerators, although the
model relies on linearity of the phenomenon, and ignore
so me complexity.
2. The Acoustic Properties of a Regenerator
The gas flow in the regenerator is considered as periodic
one-dimensional unsteady flow. The interaction between
porous material and working medium leads to the fol-
lowing equations that describe the propagation of the 1Corresponding aut h or, Fax:[phone].

G. Z. DING ET AL. 17
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
sound waves in a “porous medium”:
2
2
20
z
PP
zc




 
(1)
2
zz
v
j
P
z
c



 (2)
where P is sound pressure,
1
p
z
p
c
c
s
j




,
2
2
p
p
z
z
c
c

 ,
p
f

 it denotes the density of the medium inside the
material; , is air/porous mate-
rial coupling factor.
2(1
ps
sRjK   )

is angular frequency. While the
porosity and the density of the porous material can be
measured easily, the definition of sound velocity
p
c
needs a hypothesis about the thermodynamic process that
the fluid undergoes inside the porous material.
Generally porous materials have a complex propaga-
tion constant 0

and acoustic impedance 0
Z
. The real
part of the propagation constant is directly related to
sound wave attenuation inside the porous material; the
acoustic impedance is high at low frequency and asymp-
totically tends to that of the medium at higher frequen-
cies.
A volumetric porosity

is defined simply as the ra-
tio of connected void volume to the total volume
of the sample regenerator , and hydraulic diameter
are defined as follow s:
void
V
ltota
V
void
total
V
V
  (3)
4(1 )
h
rd


 (4)
These quantities are easy to measure accurately for
stacked screens. As the frequency increases, the viscous
penetration depth decreases, so the mesh of stacked
screens need be chosen with the resonance frequency of
the thermo-acoustic engine. The loss of the regenerator is
a very difficult term because the heat transfer process has
some complexity such as the presence of heat exchang-
ers, minor losses associated with an abrupt ch ange in the
cross section of the flow passage. Its viscous distribution
function v and heat distribution function k, mainly
dependent on the geometry of regenerator channels, their
expression for cylinders only as follows:
h h


 



  
01
00
01
00
(1)/2 (1)/
,
(1)/(1)/ (1)/
(1)/2 (1)/
,
(1)/(1)/ (1)/
vh
vv
hvhv hv
h
hh
Ji rJi r
hf
Ji ri rJi r
Ji rJi r
hf
Ji ri rJi r


v
h














(5)
v
f
and k
f
denotes spatial-mean values of viscous
distribution function and heat distribution function,
where J is Bessel function. 2/
kk

  is the fluid’s
thermal penetration depth, and
0
p
K
kc

 is its thermal
diffusivity. 2
v



 is the viscous pen et rat i on depth.
3. Active Network for No Isothermal
Regenerators
An actual regenerator possesses longitude temperature
oscillation and longitude pressure oscillation, and there
is transverse temperature oscillation in fluid about a
thermal penetration depth near the surface of solid
boundary. The major difference between regenerators
and stacks is that regenerators tend to be more like a po-
rous medium, consisting of extremely narrow, smaller
than the viscous penetration depth, tortuous paths. The
characteristics could not be described by passive network.
According to linear thermo-acoustic theory [5], regen-
erators can convert energy between thermal and acoustic
work by coupling longitude sound wave (pressure wave)
and transverse thermal wave (temperature wave), and
this can be described by two subsystems , in which sub-
system 1 links with acoustic field in regen erator chan n els
and subsystem 2 links with the thermal penetration depth.
The performance of regenerator depends on the optimi-
zation of the coupling between the two subsystems.
Nomenclature: P-sound pressure,

-frequency, c-sound velocity,
s-air/porous material coupling factor, 0

-complex propagation con-
stant,

-volumetric porosity, -hydraulic diameter, -viscous
distribution function, -heat distribution function,
h
rv h
k
hv
f
-viscous dis-
tribution function, k
f
-heat distribution function, k

thermal pene-
tration depth, v

-viscous penetration depth, J-volumetric flow rate,
Z-impedance, Y-admittance, -Prandtl number, Pr 0

- mean density,
A
-channel area,

-ratio of specific heats, -average temperature,
m
T
'
A
-transport matrix, Re-real of complex number,

-phase shift,
-temperature difference. T
For an actual regenerator with temperature gradient, a
capillary model is adopted in regenerator channels. By
solving basic control equations (mass conversation equa-
tion, momentum equation, energy equation and state

18 G. Z. DING ET AL.
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
equation) under the condition of known boundary, the
transport equations for no isoentropy oscillation can be
obtained as follows [6-8]:
PZJ
z
JYP J
z






 


(6)
where P is the ordinary pressure wave and J is volumet-
ric flow rate, 0
(1 )
v
i
Z
A
f

,
0
[1 (1)]
iA
Y
pf



,
1
(1 )(1)
kv m
rvm
f
fd
PfTd



T
z
.
Z is the impedance and Y is admittance per unit length
of channel ,, Pr 0

, A,

,

, are the fluid’s
Prandtl number, mean density, channel area of regenera-
tor , ratio of specific heats, average temperature and an-
gular frequency respectively.
m
T
The second term of Equation (6) in the right is a
source, it denotes a flow source, where

is the
thermo-acoustic source parameter of the regenerator. On
one hand, it is confirmed by mathematically configura-
tion of Equation (6). On the other hand, position oscilla-
tion of medium results in pressure oscillation of medium
in control volume physically, temperature variation and
density variation. The density oscillations in the thermal
boundary layer act as a volume flow source and result in
the change of velocity oscillation. The temperature
variation produces a source in the flow field, and these
characteristics can be called flow source [6,8]. The input
power deposited in acoustic field prompts pressure os-
cillation interfering with impedance. So there are a flow
source in no isothermal capillary network, this is J

.
The thermo-acoustic source parameter

is also called
as flow amplification factor. The flow gain J

pro-
duced by flow source will increase the acoustic field in
regenerator medium (acoustic workJ

), and in the
end of the regenerator stable acoustic work output can be
obtained.
According to network theory [5,8], flow process of
no isothermal tubes of ideal small length in terms of
Equation (6) can be expressed for an active network as
Figure 1 shown.
The transport equations responding to Figure 1 are
expressed as:
1
()( )
11
()1( )
11
()
()
Yz Zz
Zz
PzPz z
zz
J
zYz Jz
zz
Pz z
AJz z


 

 






z













 







o
o
P
(7)
where is a transport matrix. For the tube whose
length is l, its network is made up of many such net-
works shown as Figure 1, so we can obtain:
'
A
11 12
21 22
()
ioo
k
ioo
PPP
AA
AA
AA
J
JJ J

  

 

  



 

(8)
where i and o denote input and output.
Figure 1. Schematic diagram of type network model. 
4. H Matrix Model and Identification
4.1. H Matrix Model
Obviously, it is not convenient to use Equation (8) to
calculate the network. For quantifying the network,
Equation (6) can be modified as:
2
2
2
2
0
0
PP
YZP
z z
JJ
YZJ
zz














(9)
where

, Y, Z are spacial mean value of responding
parameter, approximately substitute for middle value in
the regenerator. Solving Equation (9) with boundary P(0)
and J0 and from Equatio n (6), we can obtain:
11 12 ()(0) (0)PzH PHJ



 (10)
21 22
()(0) (0)
J
zHP HJ



 (11)
where 1221
11
12
exp()exp( )z
Hz

 


 (12)
1221
12
12
[ exp()exp()]
Z
z
H




z
(13)
1221
21
12
[ exp()exp()]Yz
H




z
(14)

G. Z. DING ET AL. 19
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
112 2
22
12
exp()exp()z
H




z
(15)
2
111 4
22 YZ
   , 2
211 4
22 YZ
 
According to above equations, the output of acoustic
work in the regenerators depends on flow source pa-
rameters

. As

=0, above equations are transport
equations for isothermal regenerator, they are ideal
transport equations; As 0

, the network is equi-
valent with self-actuated oscillation shown as Figure 2,
where direct power supply corresponds to input heat, and
sound oscillation induced by solid medium cooperating
with gas micro mass in regenerator channels corresponds
to self-actuated oscillation.
Suppose z=l in Equations (10) and (11), transport
equations for channel length l are obtained:
(16)
() (0)
() (0)
Pl P
H
Jl J
 

 
 



where .
11 121112
21 2221 22
zl
HH HH
HHH HH







Regenerators can be regarded as capillary bundles
made up of N capillary. Accord ing to network character-
istics:
() (0)
()/ (0)/
Pl P
H
J
lNJ N










(17)
Equation (17) becomes
(18)
11 12
21 22
/ () (0)
() (0)
HHN Pl P
HN H
Jl J

 

 
 

4.2. Identification of H Matrix
Capillary number N are regarded as identification pa-
rameter x, Equation (18) becomes
12
11 00
21022 0
l
l
H
PHP J
x
J
HxP HJ





(19)
The acoustic work of regenerators can be obtained as:
**
00
11
Re() ()
22
i
illii
B
WPJPJAx
x

i
C
1i
i
(20)
where ,
2*
0112
Re[ ]
ii
AP HHi2*
01
222
Re[ ]
ii
BJ HH
****
11 22001221 00
Re[( 1)]
i
CHHPJHHPJ
Re denotes the real of complex number. i stands for
Figure 2. Self-actuated oscillation.
experiment number. System identification adopts ex-
treme theory, by solving function ()Wx
, the minimum
of target functional analysis can be obtained. When
theoretical ()Wx
 shows an optimal agreement with
measured i
W

, x is an optimal evaluation. Error law
function can be expressed as [11]:
2
1
() ()
2i
ii
i
B
FxAxC W
xi


 




 (21)
In order to get the minimum of error law function, let
0
F
x


, we can obtain :
43 0xbxdxe

 (22)
where 2
(2)
ii i
i
i
i
A
CW
bA




, 2
(2
ii i
i
i
i
BC W
dA



)
,
2
2
i
i
i
i
B
e
A



There should be 4 solutions. The right one can be
chosen by mesh numbers and hydraulic diameter.
5. Experimental Identification
5.1. Experimenta l A pparatus
In order to identify the H matrix, a regenerator test ap-
paratus with external actuator has been established, and
its configuration is shown as Figure 3 and Figure 4. Input
work is given by linear compressor, amplified output
work is measured at the work receiver of an orifice valve
and a buffer. In experiments, the helium gas as working
medium is charged at 1.0MPa, while four kinds of dense
meshes (#120, #150, #200, #250) were tested. Their
geometric properties are shown as table 1. The pressures
at two end of regenerator are measured by two piezo-
electricity sensors of type CY-Yd-203, their signals are
amplified by electric charge amplifier of type YE5853,
and their phase shift is measured by SR830 DSP lock-in
amplifier. The working frequency of linear compressor
can be regulated by signal source. The hot heat ex-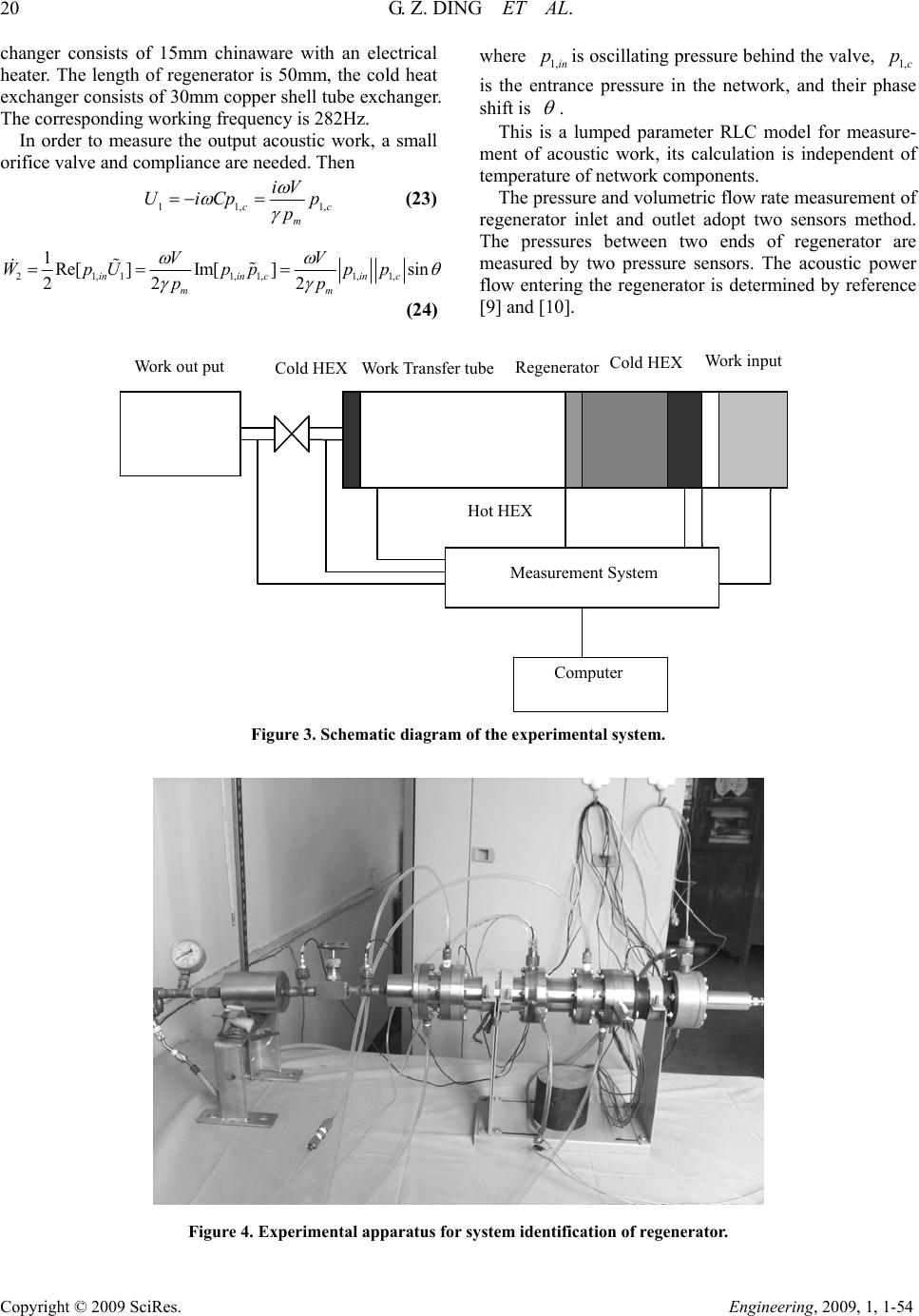

20 G. Z. DING ET AL.
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
changer consists of 15mm chinaware with an electrical
heater. The length of regenerator is 50mm, the cold heat
exchanger consists of 30mm copper shell tube exch anger.
The corresponding working frequency is 282Hz.
where is oscillating pressure behind the valve,
is the entrance pressure in the network, and their phase
shift is
1, in
p1,c p

.
This is a lumped parameter RLC model for measure-
ment of acoustic work, its calculation is independent of
temperature of network components.
In order to measure the output acoustic work, a small
orifice valve and compliance are needed. Then
11,c
m
iV
UiCp p
p

  The pressure and volumetric flow rate measurement of
regenerator inlet and outlet adopt two sensors method.
The pressures between two ends of regenerator are
measured by two pressure sensors. The acoustic power
flow entering the regenerator is determined by reference
[9] and [10].
1,c
(23)
21,11, 1,1,1,
1Re[ ]Im[]sin
22 2
inin cinc
mm
VV
WpUpp pp
pp



 
 
(24)
Work input Cold HEX
Work out put Regenerator
Work T ransfer tube
Cold HEX
Computer
Measurement System
Hot HEX
Figure 3. Schematic diagram of the experimental system.
Figure 4. Experimental apparatus for system identification of regenerator.

G. Z. DING ET AL. 21
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
Table 1. Geometric properties of regenerator Specimens
(regenerator length=50mm,inner diameter=22mm).
Type of wire
screen Mesh num- ber/cm Hole diame- ter(mm) Wire diame- ter(mm) Porosity (%) Hydraulic diame- ter(um)
80 31.5 0.198 0.12 70.3 71.1
120 47.2 0.132 0.08 70.3 47.4
150 59.1 0.104 0.065 69.8 37.7
200 78.7 0.074 0.053 67.2 27.2
The stacked screen is made up of #200 wire meshes
(Table 1), its porosity is 0.672, and the temperature dif-
ference between the two ends of regenerator is 226K
（the
whole experimental range is 220K~400K）, and the
oscillating frequency dependence can be found in Ref-
erence [9].
5.2. Experimental Results
Based on the experiment, the relation between the capil-
lary number and wire meshes is shown as Figure 5 ac-
cording to Equation (22). The calculated data and meas-
ured data of output acoustic work in regenerator after
identification are shown as Figure 6 (for meshes #200).
The error in the dimension measurements is less than
1.0%. The thermocouples with an accuracy of

0.75%
are utilized to measure both fluid and wall temperature.
The error between measured and calculated acoustic
work is less than 3% according to Figure 6.
The output acoustic work and COPR of regenerators
for different wire meshes are shown as follows:
From Figure 7, the length of regenerators need be
chosen accurately. The meshes of regenerators must
match with the working frequency of thermo-acoustic
engines.
80100 120 140 160 180 200
150
200
250
300
350
400
450
500 024681
0
2
4
6
8
10
0
x(capillary number)
wire meshes
Figure 5. The relation of the identified capillary number
and wire meshes.
300 320 340 360 380 400 420 440 460
16
18
20
22
24
26
28
30
32
34
36
02468
0
2
4
6
8
10
10
the output acoustic work(W)
temperat ure difference(K)
calculation
experiment
Figure 6. The relation of the output work and temperature
difference of regenerator.
0.00 0.01 0.020.030.04 0.050.060.070.08 0.09 0.10
0
10
20
30
40
50
60
70
80
the output acoustic work(W)
the length of regenerator(m)
80 mesh
120mesh
150mesh
200mesh
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10
0.00
0.05
0.10
0.15
0.20
0.25
0.30
0.35
0.40
0.45
0.50
COPR
the length of regenerat or
80 mesh
120mesh
150mesh
200mesh
Figure 7. The output acoustic work and COPR of regenerators.

22 G. Z. DING ET AL.
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
6. Conclusions
The lumped parameter H matrix of regenerator network
is derived by establishing an active thermo-acoustic
network model of regenerator, and identification pa-
rameters using capillary number N of system network
are identified. The calculated results and measured data
of output acoustic work in regenerators show a well
agreement by identifying H matrix. The identified H
matrix provides convenience for engineering calculation
of regenerator, and provided a basis for whole network
of thermo-acoustic engines.
7. Acknowledgements
The paper is supported by the Natural Science Fund of
P. R. China (project No. 50676068).
8. References
[1] J. Gary, D. E. Pancy, and R. Radebaugh, “A computa-
tional model for a regenerator,” in: Proceedings of Third
Cryocooler Conference, NIST Special Publication, Vol.
698, pp.199-211, 1985.
[2] Y. Matsubara, “Effect of void volume in regenerator,” in:
Proceedings of The Sixth International Cryocooler Con-
ference, 1990.
[3] K. Nam and S. Jeong, “Novel flow analysis of regenera-
tor under oscillating flow with pulsating pressure,”
Cryogenics, Vol. 45, pp. 368-379, 2005.
[4] Y. Y. Chen, E. C. Luo, and W. Dai, “Heat transfer charac-
teristics of oscillating flow regenerator filled with circular
tubes or parallel plates,” Cryogenics, Vol. 47, pp. 40-48,
2007.
[5] G. W. Swift, “Thermoacoustic engines,” Journal of the
Acoustical Society of America, Vol. 84, No. 4, pp.
1145-1179, 1988.
[6] X. H. Deng, “Thermoacoustic theory of regenerator and
design theory for thermoacoustic engine [D],” Wuhan:
Huazhong University of Science and Technology, 1994.
[7] F. Wu, et al., “Active network modeling for regenerator
cryocooler [A],” Proceedings of Symposium on Energy
Engineering in the 21st Century [C], Begell House New
York, Wallingford, 2000.
[8] F. Z. Guo, “Dynamic heat transfer [M],” Wuhan:
Huazhong University of Science and Technology Press,
1997.
[9] Q. Tu, Q. Li, F. Wu, and F. Z. Guo, “Network model ap-
proach for calculating oscillating frequency of ther-
moacoustic prime mover,” Cryogenic, Vol. 43, pp. 351-
357, 2003.
[10] Q. Tu, C. Wu, Q. Li, F. Wu, and F. Z. Guo, “Influence of
temperature gradient on acoustic characteristic parame-
ters of stack in TAE,” International Journal of Engineer-
ing Science, Vol. 41, pp. 1337-1349, 2003.