A Scalable Model of the Substrate Network in Deep n-Well RF MOSFETs with Multiple Fingers

doi:10.4236/cs.2011.22014

Circuits and Systems, 2011, 2, 91-100

doi:10.4236/cs.2011.22014 Published Online April 2011 (http://www.SciRP.org/journal/cs)

A Scalable Model of the Substrate Network in Deep N-Well

RF MOSFETs with Multiple Fingers

Jun Liu1,2, Maris sa Condon2

1Key Laboratory of RF Circuits and Systems, Ministry of Education, Hangzhou Dianzi University, Hangzhou, China

2School of Electronic Engineering, Dublin City University, Dublin, Ireland

E-mail: ljun77@163.com

Received January 18, 2011; revised March 4, 2011; accepte d M arch 11, 2011

Abstract

A novel scalable model of substrate components for deep n-well (DNW) RF MOSFETs with different num-

ber of fingers is presented for the first time. The test structure developed in [1] is employed to directly access

the characteristics of the substrate to extract the different substrate components. A methodology is developed

to directly extract the parameters for the substrate network from the measured data. By using the measured

two-port data of a set of nMOSFETs with different number of fingers, with the DNW in grounded and float

configuration, respectively, the parameters of the scalable substrate model are obtained. The method and the

substrate model are further verified and validated by matching the measured and simulated output admit-

tances. Excellent agreement up to 40 GHz for configurations in common-source has been achieved.

Keywords: Deep N-Well (DNW), RF Mosfets, Substrate Network, Scalable Model

1. Introduction

THE incorporation of a Deep N-Well (DNW) implantation

into a standard CMOS technology has become a popular

choice for reducing undesired interference in CMOS

mixed-signal/RF SoC designs [2-6]. Substrate network

parameters are of the utmost importance in accurately

modeling the output admittance of RF MOSFETs. For

mixed-signal/RF SoC design, a scalable model of RF

MOSFETs is useful. Many papers have reported about

scalable models of substrate network components [7-13].

However, there are few detailed works on scalable mod-

els with substrate network components in DNW RF

MOSFETs with different number of fingers. In contrast

to the RF MOSFET without DNW implantation (as seen

from the nMOSFETs in Figure 1), the DNW actually

partitions the substrate of a DNW RF MOSFET into three

parts [1]: The DNW itself, the p-well in the DNW, and

the original substrate where the DNW is formed. The

DNW layer forms a capacitive coupling path in the sub-

strate, which exists no matter what the electrical con-

figuration is. Furthermore, most previous works [7-19]

dealt with substrate parasitic effects in RF MOSFETs by

using resistance networks only. The capacitive coupling

effect, which is physically in existence, is always ne-

glected. All of these make the previously reported sub-

strate models less physically reasonable to use for accu-

rately extracting the substrate network components of

DNW RF MOSFETs.

In this paper, a compact, physically based substrate

network is proposed targeted specifically at DNW RF

MOSFET modeling. A novel test structure proposed in

[1] is expanded and employed in deriving and extracting

the Nf - dependent equations involving substrate compo-

nents in multi-finger DNW RF MOSFETs. The geomet-

ric effects such as shallow trench isolation (STI), which

have never been considered in previous reported works,

are accurately modeled. The results show that the sub-

strate components within the p-well and th e capacitances

caused by the DNW are strongly dependent on Nf, while

the parasitic components in the original p-substrate have

a slight depe n dence on Nf in multi-finge r devices.

To verify the validity of the derived scalab le model of

the substrate network components, a macro-model con-

sisting of the BSIM3v3.2 model core with the proposed

substrate-network based on the extracted parameters, is

simulated in Agilent Advanced Design System (ADS).

Excellent agreement between the simulated and meas-

ured output admittance for a set of devices with different

number of fingers up to 40 GHz validated the accuracy

of the methodology proposed for DNW RF-MOSFET

modeling in this paper.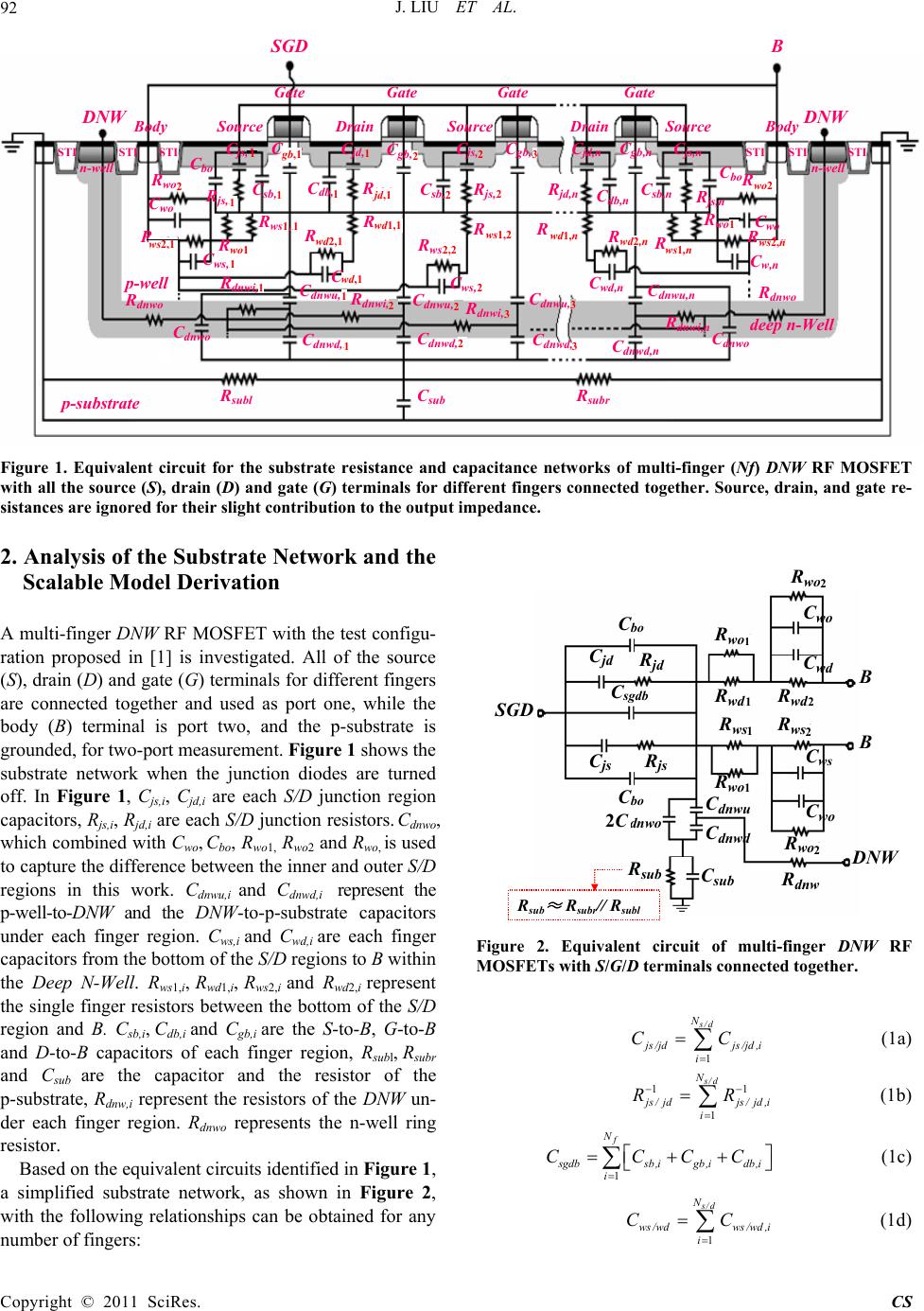

J. LIU ET AL.

92

DNW

C

db,1

C

gb,1

C

bo

C

js,1

R

js,1

C

dnwo

C

sub

R

subl

R

subr

C

ws,1

R

ws1,n

R

ws2,n

R

ws1,1

C

wo

R

wo2

C

wo

R

wo2

C

dnwo

C

dnwd,1

C

dnwu,1

C

dnwd,2

C

dnwu,2

C

dnwd,3

C

dnwu,3

C

dnwd,n

C

dnwu,n

C

bo

C

js,n

R

js,n

C

sb,1

C

jd,1

R

jd,1

C

gb,n

C

sb,2

C

gb,2

C

js,2

R

js,2

C

gb,3

C

db,n

C

sb,n

C

jd,n

R

jd,n

R

ws2,1

R

wd2,1

R

wd1,1

C

wd,1

R

ws2,2

R

ws1,2

C

ws,2

R

wd2,n

R

wd1,n

C

wd,n

C

w,n

p-substrate

p-well

STI STISTI STI

SourceDrainSourceDrain Source

GateGate GateGate

deep n-Well

Body Body

R

dnwo

R

dnwo

R

dnwi,n

R

dnwi,3

R

dnwi,2

R

dnwi,1

B

S

GD

n-well n-well

STISTI

DNW

R

wo1

R

wo1

Figure 1. Equivalent circuit for the substrate resistance and capacitance networks of multi-finger (Nf) DNW RF MOSFET

with all the source (S), drain (D) and gate (G) terminals for different fingers connected together. Source, drain, and gate re-

sistances are ignored for their slight contribution to the output impedance.

2. Analysis of the Substrate Network and the

Scalable Model Derivation

A multi-finger DNW RF MOSFET wi th the test configu-

ration proposed in [1] is investigated. All of the source

(S), drain (D) and gate (G) terminals for diff erent fingers

are connected together and used as port one, while the

body (B) terminal is port two, and the p-substrate is

grounded, for two-port measurement. Figure 1 shows the

substrate network when the junction diodes are turned

off. In Figure 1, Cjs,i, Cjd,i are each S/D junction region

capacitors, Rjs,i, Rjd,i are each S/D junction resistors. Cdnwo,

which combined with Cwo, Cbo, Rwo1, Rwo2 and Rwo, is used

to capture the difference between the inner and outer S/D

regions in this work. Cdnwu,i and Cdnwd,i represent the

p-well-to-DNW and the DNW-to-p-substrate capacitors

under each finger region. Cws,i and C

wd,i are each finger

capacitors from the bottom of the S/D regions to B within

the Deep N-Well. Rws1,i, Rwd1,i, Rws2,i and R

wd2,i represent

the single finger resistors between the bottom of the S/D

region and B. Csb,i, Cdb,i and Cgb,i are the S-to-B, G-to-B

and D-to-B capacitors of each finger region, R

subl, Rsubr

and C

sub are the capacitor and the resistor of the

p-substrate, Rdnw,i represent the resistors of the DNW un-

der each finger region. Rdnwo represents the n-well ring

resistor.

Based on the equivalen t circuits iden tified in Figure 1,

a simplified substrate network, as shown in Figure 2,

with the following relationships can be obtained for any

number of fi ng ers :

B

C

bo

C

sgdb

C

jd

R

js

2C

dnwo

R

sub

C

js

R

ws1

R

jd

R

wd1

C

sub

B

C

dnwd

C

dnwu

C

bo

C

wd

R

wd2

SGD R

ws2

C

ws

C

wo

R

wo2

R

wo2

C

wo

R

dnw

DNW

R

sub

≈

R

subr

// R

subl

R

wo1

R

wo1

Figure 2. Equivalent circuit of multi-finger DNW RF

MOSFETs with S/G/D terminals connected together.

1

s/d

N

j

s /jdjs /jd ,i

i

CC



 (1a)

11

1

s/d

N

j

s /jdjs/jd ,i

i

RR





 (1b)

1

f

N

s

gdbsb,igb,idb,i

i

CCCC













 (1c)

1

s/d

N

ws /wdws /wd ,i

i

CC



 (1d)

wo1

wd2,1

wd,1

wd1,1

jd,1

ws1,2 wd1,n

3

2

2,2

2

1

2 1

12

3

2

1

wo2

1

ws1,n

wd

2

,

n

1

2

3

1

ws2

,

1

2

1

2

1

2

2C

g

b,1

ws2

,

n

J. LIU ET AL.

93

11

11 11

1

s/d

N

ws/ wdws/ wd,i

i

RR





 (1e)

111

s

ubsubl subr

RRR



 (1f)

11

22 22

1

s/d

N

ws/ wdws/ wd,i

i

RR





 (1g)

1

f

N

dnwu dnwu,i

i

CC













 (1h)

1

f

N

dnwddnwd ,i

i

CC













 (1i)

1

2f

N

dnw dnwodnw,i

i

RR R























 (1j)

where, Cjs, Cjd represent the total S/D junction region

capacitances, Rjs,, Rjd represent the total S/D junction re-

sistances, Rsub represents the total resistance of the

p-substrate, Cdnw represents the total capacitance caused

by the DNW, Cws, Cwd are the total capacitances from the

bottom of the S/D regions to B within the Deep N-Well,

Rws1/wd1 and Rws2/wd2 are the total resistances between the

bottom of the S/D regions and B within the Deep N-Well

and Ns and Nd represent the numbers of source and drain

diffusion regions, respectively. In the model, when the

number fing ers is odd, Ns = Nd = (Nf + 1)/2. Ns = Nf/2 + 1

and Nd = Nf/2 when the number of fingers is even.

Assuming that there are no differences in the inner S/D

regions, the above equations, (1a)-(1h), can be formed as

follows:

j

s/jds/dj,i

CNC (2a)

j

s/ jdj/is/d

RRN (2b)

2

s

gdbfsdb,igb,i

CNCC







(2c)

ws/wds/ dw,i

CNC (2d)

1

11 w,i

ws/wd

s

/d

R

RN

 (2e)

2

22 w,i

ws/wd

s

/d

R

RN

 (2f)

dnwuf dnwu,i

CNC (2g)

dnwdfdnwd,i

CNC (2h)

2dnwi

dnw dnwo

f

R

RRN



(2i)

where

j

,i js,i jd,i

CC C



j

,i js,i jd,i

RR R,

s

db sb,idb,i

CCC

w,iws,iwd,i

CC C



,11 1w,iws,iwd,i

RR R

and 22 2w,iws,iwd,i

RR R.

In this paper, the following equations are used to em-

pirically model the Nf - dependence of Rsub and Csub:

s

ubsubIfsubunit

RRNR



 (2j)

s

ubsubIfsubunit

CC NC



 (2k)

where RsubI and CsubI represent the p-substrate resistance

and capacitance of a one-finger device, Rsubunit and Csubunit

are used to explain the increase in Rsub and Csub with the

increase in the number of gate fingers.

3. Scalable Model Parameter Extraction

In order to accurately predict the scalability of the sub-

strate elements, a direct parameter extraction methodol-

ogy is of the utmost importance. In this work, two dif-

ferent test configurations are used. One has the DNW

floating (as shown in Figure 3(a)) and the other has the

DNW grounded (as shown in Figure 4(a)). In each case,

all S/D/G terminals for different fingers are connected

together as port one, the B terminal is port two, and the

p-substrate grounded. The equivalent circuits shown in

Figure 3(b) and Figure 4(b) can easily be derived from

the complete equivalent circuit shown in Figure 2, for

SSSSSSS

DDDDDDD

SS

Source (S)

Drain (D)

Gate (G)

SGD

DNW

Metal Level 1( M1 )n-well

Body

(B)

(a)

(M1)

D

N

W

n-well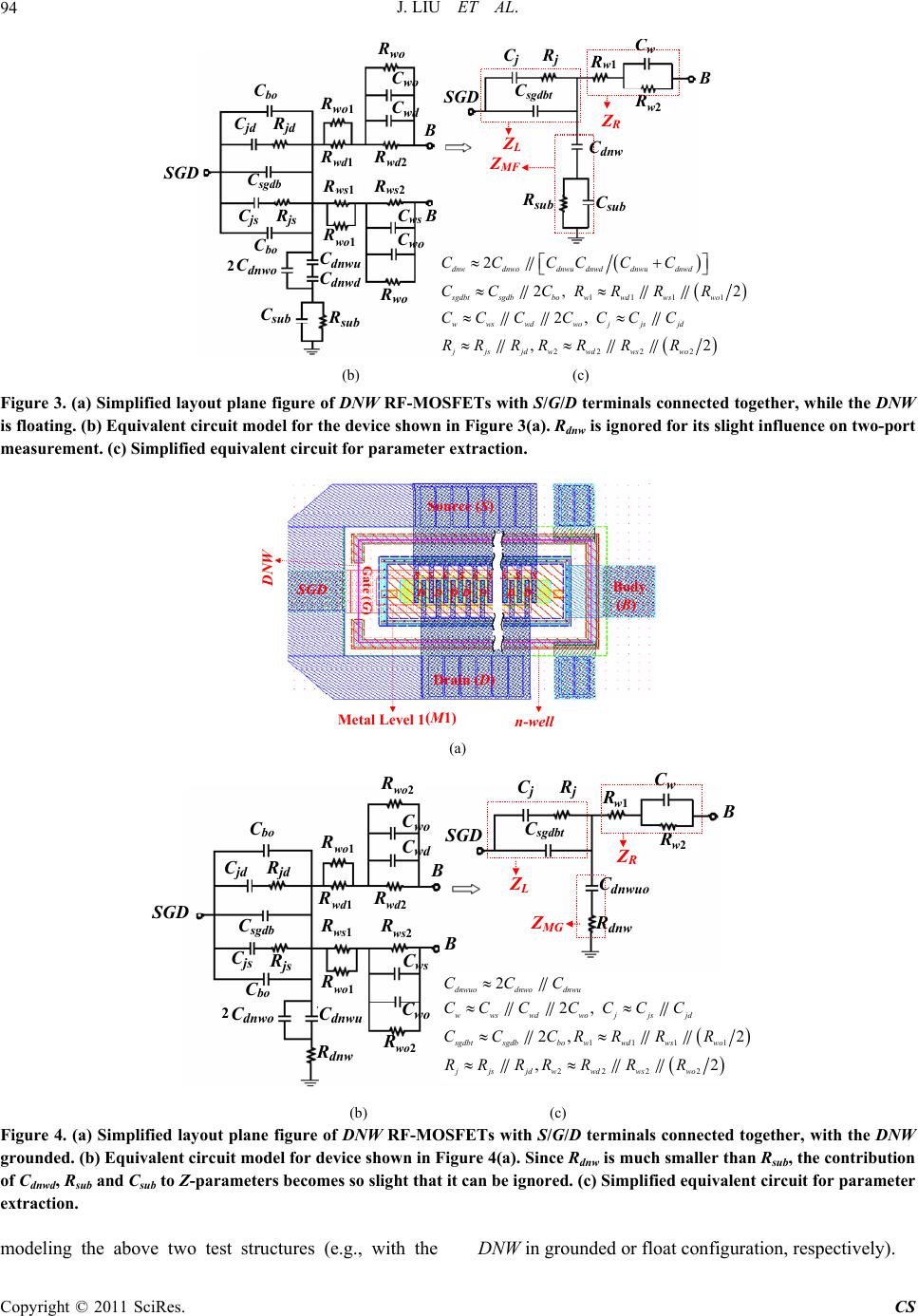

J. LIU ET AL.

94

B

C

bo

C

sgdb

C

jd

R

js

2C

dnwo

R

sub

C

js

R

ws1

R

jd

R

wd1

C

sub

B

C

dnwd

C

dnwu

C

bo

C

wd

R

wd2

B

SGD

C

j

R

j

C

w

R

w1

R

w2

C

dnw

C

sub

R

sub

C

w

≈

C

ws

//C

wd

//2C

wo

,C

j

≈

C

js

// C

jd

R

j

≈

R

js

// R

jd

,

R

w1

≈

R

wd1

// R

ws1

//(R

wo1

/2)

R

w2

≈

R

wd2

//R

ws2

// (R

wo2

/2)

C

sgdbt

≈

C

sgdb

//2C

bo,

R

ws2

C

ws

C

wo

R

wo

R

wo

C

wo

C

sgdbt

C

dnw

≈

2C

dnwo

//[C

dnwu

C

dnwd

/(C

dnwu

+C

dnwd

)]

SGD

Z

L

Z

MF

Z

R

wo1

R

wo1

(b) (c)

Figure 3. (a) Simplified layout plane figure of DNW RF-MOSFETs with S/G/D terminals connected together , while the DNW

is floating. (b) Equivalent circuit model for the device shown in Figure 3(a). Rdnw is ignored for its slight influence on two-port

measurement. (c) Simplified equivalent circuit for parameter extraction.

SSSSSSS

DDDDDDD

SS

Source (S)

Drain (D)

Gate (G)

SGD

Metal Level 1( M1 )n-well

Body

(B)

DNW

(a)

B

C

bo

C

sgdb

C

jd

R

js

2C

dnwo

C

js

R

ws1

R

jd

R

wd1

B

C

dnwu

C

bo

C

wd

R

wd2

B

SGD

C

j

R

j

C

w

R

w1

R

w2

C

dnwuo

C

w

≈

C

ws

//C

wd

//2C

wo

,C

j

≈

C

js

// C

jd

R

j

≈

R

js

// R

jd

,R

w2

≈

R

wd2

//R

ws2

// (R

wo2

/2)

C

sgdbt

≈

C

sgdb

//2C

bo,

R

ws2

C

ws

C

wo

R

wo2

R

wo2

C

wo

C

sgdbt

C

dnwuo

≈

2C

dnwo

//C

dnwu

SGD

R

dnw

R

dnw

Z

L

Z

MG

Z

R

wo1

R

wo1

R

w1

≈

R

wd1

//R

ws1

// (R

wo1

/2)

(b) (c)

Figure 4. (a) Simplified layout plane figure of DNW RF-MOSFETs with S/G/D terminals connected together, with the DNW

grounded. (b) Equivalent circuit mode l for devic e show n in Figure 4(a). Since Rdnw is much smaller than Rsub, the contribution

of Cdnwd, Rsub and Csub to Z-parameters becomes so slight that it can be ignored. (c) Simplified equivalent circuit for parameter

extraction.

modeling the above two test structures (e.g., with the DNW in grounded or float configuration, respectively).

1

wd1 wd2

ws2

ws1

wo1

2

w2

w1







1111

222 2

2

2, 2

2,

,2

dnwdnwodnwu dnwddnwudnwd

sgdbtsgdbbo wwdwswo

wws wdwojjsjd

jjsjd wwdwswo

CC CCCC

CC CRRRR

CCCCCCC

RR RRRRR













 



(M1) n-well

DNW

wo2

wo1

wd2wd1

ws2

ws1

wo1

wo2

w2

2



111 1

222 2

2

2,

2, 2

,2

dnwuodnwo dnwu

wws wdwoj jsjd

sgdbtsgdbbo wwdwswo

jjsjd wwdwswo

CCC

CCCCCCC

CC CRRRR

RR RRRRR







 



w1

J. LIU ET AL.

95

As seen from Figure 3(b) and Figure 4(b), since the

topologies from S to B are the same as that from D to B,

both of the equivalent circuits shown in Figure 3(b) and

Figure 4(b) can be reduced to T-networks by using sim-

ple approaches as shown at the bottom of Figure 3(c)

and Figure 4(c). Based on (2a)-(2i) and the approaches

used to simplify Figure 3(b) and Figure 4(b) to Figure

3(c) and Figure 4(c), respectively, the elements of the

two T-networks shown in Figure 3(c) and Figure 4(c)

can be calculated with the following equations:



1

j

fj,i

CN C (3a)



1

jj,if

RR N (3b)



21

wwofw,i

CCNC (3c)







11

1

11

05 1

wow ,if

w

wow,if

.R RN

R.R RN





(3d)







22

2

22

05 1

wow ,if

w

wow ,if

.R RN

R.R RN





(3e)

22

s

gdbtbofsdb,i gb,i

CCNCC







(3f)

2

dnwuodnwofdnwu,i

CCNC (3g)

2

dnwdnwofdnw,i

CCNC (3h)

where

dnwu,idnwd ,i

dnw,i

dnwu,idnwd ,i

CC

CCC

 (3h.1)

Using (3h.1), Cdnw,i can be calculated as follows:

dnwu,i dnw,i

dnwd ,i

dnwu,idnw,i

CC

CCC

 (3h.2)

(2c), (2g)-(2k) and (3a)-(3h) give the Nf -dependent eq-

uations of the equivalent circuit in Figure 2. This enables

the direct identification of the scalability of the substrate

components. This will be shown later in this section.

As the ZL and ZR of the T-network shown in Figure

4(c) are the same as the ZL and ZR shown in Figure 3(c),

with the ground terminal as reference, the Z-parameters

of the T-networks shown in Figure 3(c) and Figure 4(c)

can be calculated approximately with the following equ-

ations:



1

11 12

Ldnw_ floating,dnw_ floating,

ZZZ 







1

11 12

dnw_ grounded ,dnw _ grounded ,

ZZ









22

222 222

11

jj j

s

gdbt

jj jj

CR C

jjC

CR CR







 

 (4a)

22 12

R

dnw_floating,dnw_floating,

ZZ Z





22 12dnw_ grounded ,dnw_grounded ,

ZZ





2

22

122 222 2

22

11

www

w

ww ww

RRC

Rj

RC RC





 



(4b)

12 22 2

1sub

MFdnw_ floating,

s

ub sub

R

ZZ RC







2

22 2

1

1sub sub

dnw

sub sub

RC

jj

C

RC







 (4c)

12 1

MGdnw_grounded ,dnwdnwuo

ZZ RjC



 (4d)

where Zdnw_floating and Z

dnw_grounded are measured Z-para-

meters of DNW RF MOSFETs with S/G/D terminals

connected together, when the DNW is floating or grounded,

respectively.

Further, the real and imaginary parts of the above

Z-parameter expressions can be rearranged as follows:





22

2

1

Re j

j

L

RCR

Z



 (5a)





1

222

Im 1

j

sgdbt L

j

C

CZ

CR

























(5b)



2

22

1

Im w

Rww

C

ZRC



 (5c)



2

122 2

2

Re 1w

wR

ww

R

RZ RC





 (5d)





112 2

Re

M

Fsubsub sub

Z

RRC





 (5e)









1

2222

Im 1

dnwMFsub subsub sub

CZRC/RC

 







 





(5f)





Re

dnw MG

RZ (5g)



1

Im

M

G dnwuo

ZC









 (5h)

Using (5a) and (5c), Rj and Cw can be extracted from

the slopes of the linear regression curves of the experi-

menta l







1

2Re L

Z



 and





Im

R

Z



 versus2



,

respectively. (5a) and (5c), after subtracting Rj and Cw,

give Cj and Rw2. Further, (5b) and (5d) give Csgdbt and Rw1.

Using (5e), Rsub and Csub can be determined from the

intercept of the linear regre ssion curve of th e experimen-

tal





1

M

F

Re Zversus 2



, and the slope gives Csub after

subtracting Rsub. After subtracting Rsub and Csub, (5f)

gives Cdnw. Using (5h), Cdnwuo can be extracted from the

slope of the linear regression curve of the experimental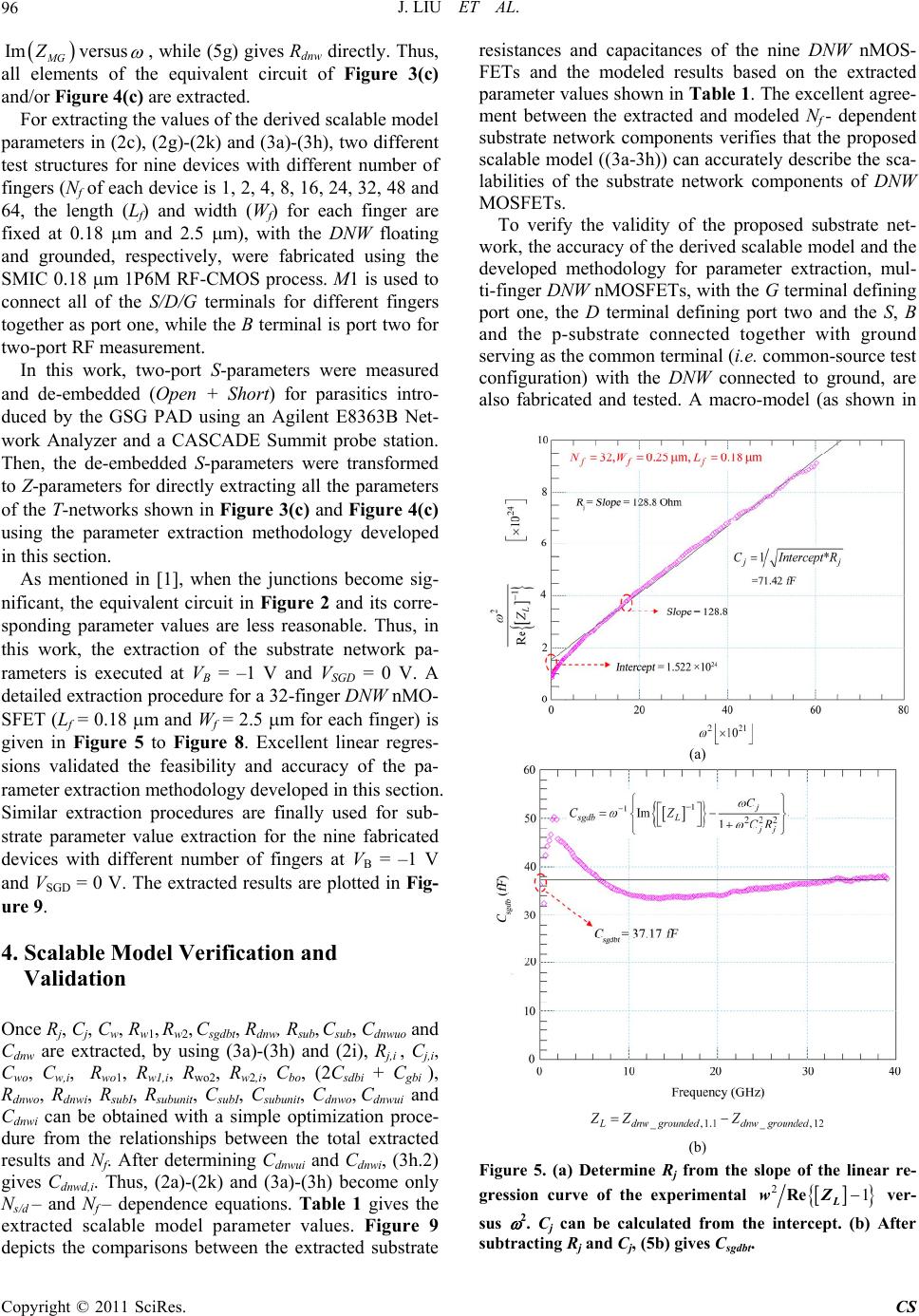

J. LIU ET AL.

96



Im

M

G

Zversus



, while (5g) gives Rdnw directly. Thus,

all elements of the equivalent circuit of Figure 3(c)

and/or F i gure 4(c) are extracted.

For extracting the values of the derived scalable model

parameters in (2c), (2g)-(2k) and (3a)-(3h), two different

test structures for nine devices with different number of

fingers (Nf of each device is 1, 2, 4, 8, 16, 24, 32, 48 and

64, the length (Lf) and width (Wf) for each finger are

fixed at 0.18 m and 2.5 m), with the DNW floating

and grounded, respectively, were fabricated using the

SMIC 0.18 m 1P6M RF-CMOS process. M1 is used to

connect all of the S/D/G terminals for different fingers

together as port one, while the B terminal is port two for

two-port RF measurement.

In this work, two-port S-parameters were measured

and de-embedded (Open + Short) for parasitics intro-

duced by the GSG PAD using an Agilent E8363B Net-

work Analyzer and a CASCADE Summit probe station.

Then, the de-embedded S-parameters were transformed

to Z-parameters for directly extracting all the parameters

of the T-networks shown in Figure 3(c) and Figure 4(c)

using the parameter extraction methodology developed

in this section.

As mentioned in [1], when the junctions become sig-

nificant, the equivalent circuit in Figure 2 and its corre-

sponding parameter values are less reasonable. Thus, in

this work, the extraction of the substrate network pa-

rameters is executed at VB = –1 V and VSGD = 0 V. A

detailed extraction procedure for a 32-finger DNW nMO-

SFET (Lf = 0.18 m and Wf = 2.5 m for each finger) is

given in Figure 5 to Figure 8. Excellent linear regres-

sions validated the feasibility and accuracy of the pa-

rameter extraction methodology developed in this section.

Similar extraction procedures are finally used for sub-

strate parameter value extraction for the nine fabricated

devices with different number of fingers at VB = –1 V

and VSGD = 0 V. The extracted results are plotted in Fig-

ure 9.

4. Scalable Model Verification and

Validation

Once Rj, Cj, Cw, Rw1, Rw2, Csgdbt, Rdnw, Rsub, Csub, Cdnwuo and

Cdnw are extracted, by using (3a)-(3h) and (2i), Rj,i , Cj,i,

Cwo, Cw,i, Rwo1, Rw1,i, Rwo2, Rw2,i, Cbo, (2Csdbi + C

gbi ),

Rdnwo, Rdnwi, RsubI, Rsubunit, CsubI, Csubunit, Cdnwo, Cdnwui and

Cdnwi can be obtained with a simple optimization proce-

dure from the relationships between the total extracted

results and Nf. After determining Cdnwui and Cdnwi, (3h.2)

gives Cdnwd,i. Thus, (2a)-(2k) and (3a)-(3h) become only

Ns/d – and Nf – dependence equations. Table 1 gives the

extracted scalable model parameter values. Figure 9

depicts the comparisons between the extracted substrate

resistances and capacitances of the nine DNW nMOS-

FETs and the modeled results based on the extracted

parameter values shown in Table 1. The excellent agree-

ment between the extracted and modeled Nf - dependent

substrate network components verifies that the proposed

scalable model ((3a-3h)) can accurately describe the sca-

labilities of the substrate network components of DNW

MOSFETs.

To verify the validity of the proposed substrate net-

work, the accuracy of the derived scalable model and the

developed methodology for parameter extraction, mul-

ti-finger DNW nMOSFETs, with the G terminal defining

port one, the D terminal defining port two and the S, B

and the p-substrate connected together with ground

serving as the common terminal (i.e. common-source test

configuration) with the DNW connected to ground, are

also fabricated and tested. A macro-model (as shown in

(a)

(b)

Figure 5. (a) Determine Rj from the slope of the linear re-

gression curve of the experimental









21



L

wZRe ver-

sus



2. Cj can be calculated from the intercept. (b) After

subtracting Rj and Cj, (5b) gives Csgdbt.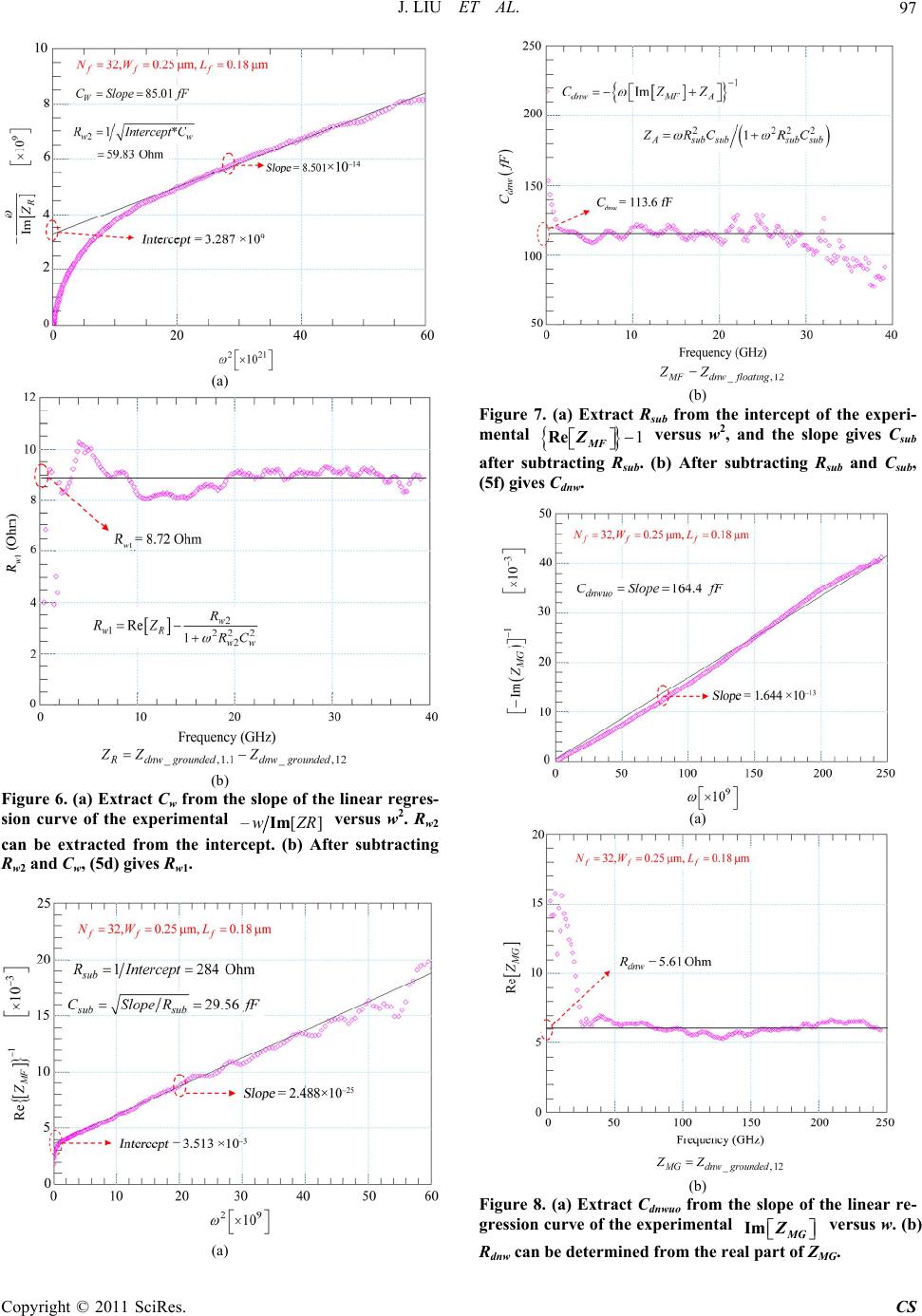

J. LIU ET AL.

97

(a)

(b)

Figure 6. (a) Extract Cw from the slope of the linear regres-

sion curve of the experimental –[]wZRIm versus w2. Rw2

can be extracted from the intercept. (b) After subtracting

Rw2 and Cw, (5d) gives Rw1.

(a)

(b)

Figure 7. (a) Extract Rsub from the intercept of the experi-

mental





1







MF

ZRe versus w2, and the slope gives Csub

after subtracting Rsub. (b) After subtracting Rsub and Csub,

(5f) gives Cdnw.

(a)

(b)

Figure 8. (a) Extract Cdnwuo from the slope of the linear re-

gression curve of the experimental 



MG

ZIm versus w. (b)

Rdnw can be determined from the real part of ZMG.

J. LIU ET AL.

98

Figure 10) for common-source connected DNW RF

MOSFETs modeling was developed. The model consists

of the BSIM3v3.2 model core with the proposed new

substrate-network and is simulated in Agilent Advanced

Design System (ADS) directly.

In Figure 10, Rg, Rd, and Rs are G, D and S terminal

series resistances, Cds is D-to-S capacitance. Cgs, and Cgd

represent the G-to-S and G-to-D capacitances, respec-

tively. Cgb, Cdb and C

sb indicate the G-to-B, D-to-B,

S-to-B capacitances, and the sum of the three compo-

nents has been extracted in section 4. A conventional

method developed in [13] is used to extract the initial

values of three terminal series resistances from de-em-

0

50

100

150

200

250

300

350

1 2 4 816243248640

500

1000

1500

2000

2500

Resistance (Ohm)

Resistance (Ohm )

R

j

R

dnw

R

w2

R

sub

R

w1

Number of fingers (N

f

)

Symbol : Measurement

Line : Proposed model

(a)

0

50

100

150

200

250

300

350

400

124816 2432 48 64

0

5

10

15

20

25

30

35

Capacitance (fF)

C

j

C

w

C

sgdbt

C

sub

C

dnw

Number of fingers (N

f

)

Symbol : Measurement

Line : Proposed model

C

dnwuo

(b)

Figure 9. (a) Extracted and modeled substrate resistances

and (b) capacitances of DNW nMOSFETs with different

number of fingers, while the length (Lf) and width (Wf) for

each finger are fixed at 0.18 m and 2.5 m.

Table 1. Extracted para meter values of the proposed model

of the substrate network in DNW RF MOSFETs

Rj,i() Cj,i(fF) Cwo(fF) Cw,i(fF) Rwo1 ()

4162 2.395 30.64 0.737 87.78

Rwo2() Rw2,i () Cbo(fF) 2Csdbi+Cgbi(fF)

203.7 2775 5.471 0.91

Rdnwi () RsubI () Rsubunit () CsubI(fF) Csubunit(fF)

73.79 282.8 0.137 26.18 0.11

Cdnwui(fF) Cdnwdi(fF) Rw1,i () Rdnwo () Cdnwo(fF)

5.045 4.771 447.7 3.46 15.2

Table 2. Values of the extracted external capacitors from

common source connected devices with different Nf, at zero

bias.(Lf = 0.18 m;Wf = 2.5 m)

Nf Cgs/d (fF)Cgb (fF) Cds (fF)

1 0.66 3.4 0.68

2 3.5 4.2 1.02

4 3.9 7.2 3.1

8 8.6 8.5 10.7

16 18.4 10.3 24.1

24 28.3 13.2 41.2

32 36.1 15.5 54.6

48 55.4 16.2 83.4

64 72.2 17.5 110.2

C

js

R

js

2C

dnwo

C

sub

R

sub

C

ws

R

ws1

R

ws2

R

wd1

G

S/B/DNW

Cds

C

jd

Rjd

R

wd2

C

wd

Rg

Rd

Rs

D

BSIM3v3.2 core

C

dnwd

C

dnwu

Cdb

Csb

C

wo

C

wo

R

wo1

R

wo2

R

wo1

R

wo2

R

dnw

Cgd

Cgb

Cgs

Cbo

Figure 10. Macro-model for DNW RF-MOSFETs modeling

when S/D junctions are not significant. The test configura-

tion with the G terminal defining port one, the D terminal

defining port two and the S, B and the p-substrate con-

nected together with ground serving as the common termi-

nal (i.e. common-source test configuration), with the DNW

is tied to ground using M1 (metal level 1), are used in

two-port measurement. All the parameters of the BSIM3v3.2,

including the terminal resistances Rd, Rg and Rs, are ex-

tracted beforehand.

bedded Y-parameters. By using the extraction method

proposed in [13], the following equations are employed

for the remaining components extraction:



12

Im

gd

Y

C



 (6a)

g

sgd

CC



(6b)





11 12

Im

g

bgd

YY

CC







(6c)

According to (1c), the total Cgb of an RF MOSFET

with the number of fingers is Nf can be calculated as fol-

lows:

w2

w

1

wo1

wo2

wd2

w

s

2

wo2

BSIM3v3.2 core

wo1

w

s

1

2

C

wd1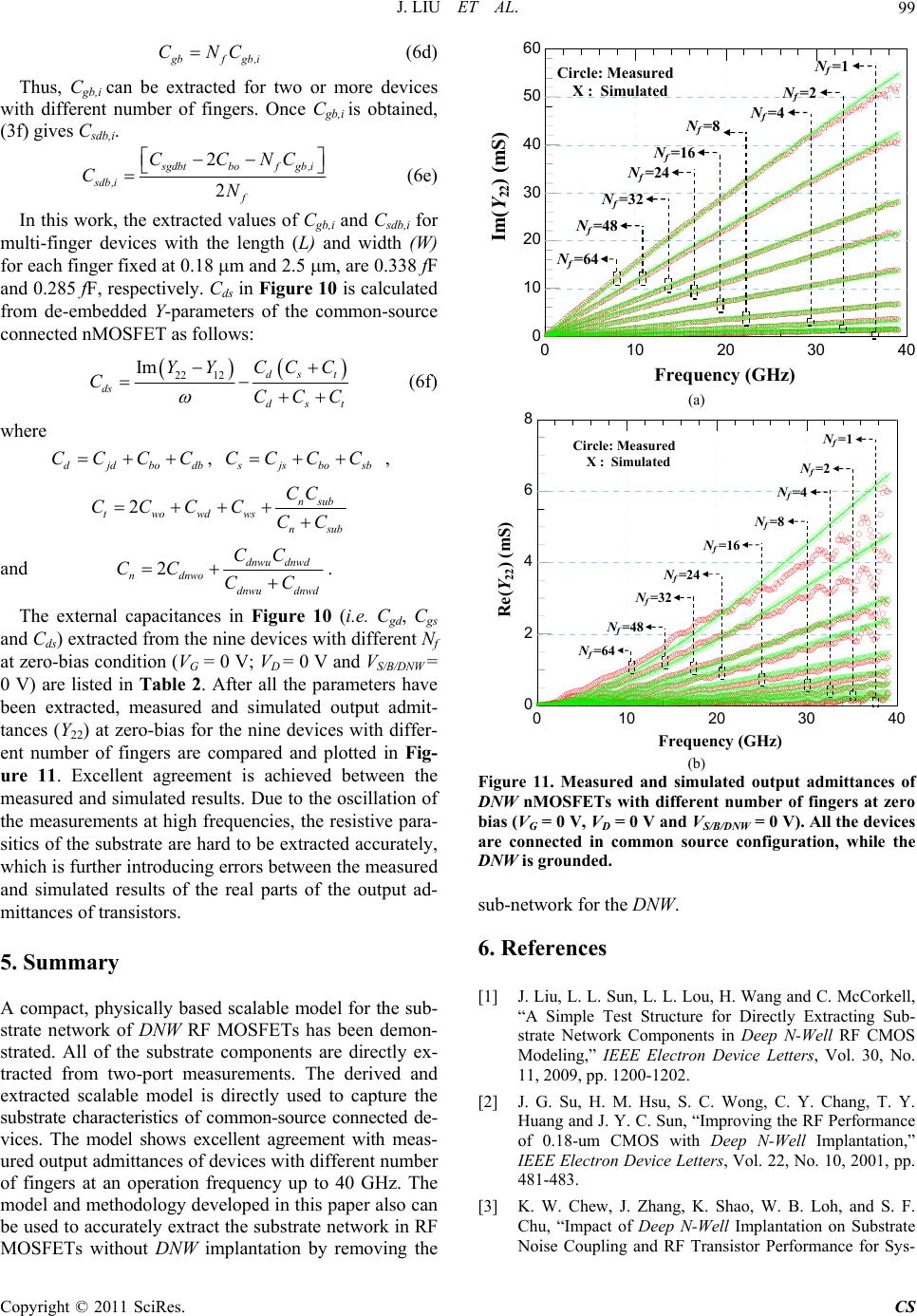

J. LIU ET AL.

99

g

bfgb,i

CNC (6d)

Thus, Cgb,i can be extracted for two or more devices

with different number of fingers. Once Cgb,i is obtained,

(3f) gives Csdb,i.

2

s

gdbtbofgb,i

sdb,i f

CCNC

CN







 (6e)

In this work, the extracted values of Cgb,i and Csdb,i for

multi-finger devices with the length (L) and width (W)

for each finger fixed at 0.18 m and 2.5 m, are 0.338 fF

and 0.285 fF, respectively. Cds in Figure 10 is calculated

from de-embedded Y-parameters of the common-source

connected nMOSFET as follows:



22 12

Im ds t

ds dst

CC C

YY

CCCC









 (6f)

where

djdbodb

CCCC,

s

js bo sb

CCC C ,

2nsub

twowdws

nsub

CC

CCCCCC





and 2dnwu dnwd

ndnwo dnwu dnwd

CC

CC CC



.

The external capacitances in Figure 10 (i.e. Cgd, Cgs

and Cds) extracted from the nine devices with different Nf

at zero-bias condition (VG = 0 V; VD = 0 V and VS/B/DNW =

0 V) are listed in Table 2. After all the parameters have

been extracted, measured and simulated output admit-

tances (Y22) at zero-bias for the nine devices with differ-

ent number of fingers are compared and plotted in Fig-

ure 11. Excellent agreement is achieved between the

measured and simulated results. Due to the oscillation of

the measurements at high frequencies, the resistive para-

sitics of the substrate are hard to be extracted accurately,

which is further introducing errors between the measured

and simulated results of the real parts of the output ad-

mittances of transistors.

5. Summary

A compact, physically based scalable model for the sub-

strate network of DNW RF MOSFETs has been demon-

strated. All of the substrate components are directly ex-

tracted from two-port measurements. The derived and

extracted scalable model is directly used to capture the

substrate characteristics of common-source connected de-

vices. The model shows excellent agreement with meas-

ured output admittances of devices with different number

of fingers at an operation frequency up to 40 GHz. The

model and methodology developed in this paper also can

be used to accurately extract the substrate network in RF

MOSFETs without DNW implantation by removing the

0 10203040

0

10

20

30

40

50

60

Im(Y

22

) (mS)

Frequency (GHz)

Circle: Measured

X : Simulated

N

f

=64

N

f

=48

N

f

=32

N

f

=24

N

f

=16

N

f

=8 N

f

=4N

f

=2

N

f

=1

(a)

0 10203040

0

2

4

6

8

Re(Y

22

) (mS)

Frequency (GHz)

Circle: Measured

X : Simulated

N

f

=64

N

f

=48

N

f

=32

N

f

=24

N

f

=16

N

f

=8

N

f

=4

N

f

=2

N

f

=1

(b)

Figure 11. Measured and simulated output admittances of

DNW nMOSFETs with different number of fingers at zero

bias (VG = 0 V, VD = 0 V and VS/B/DNW = 0 V). All the devices

are connected in common source configuration, while the

DNW is grounded.

sub-network for the DNW.

6. References

[1] J. Liu, L. L. Sun, L. L. Lou, H. Wang and C. McCorkell,

“A Simple Test Structure for Directly Extracting Sub-

strate Network Components in Deep N-Well RF CMOS

Modeling,” IEEE Electron Device Letters, Vol. 30, No.

11, 2009, pp. 1200-1202.

[2] J. G. Su, H. M. Hsu, S. C. Wong, C. Y. Chang, T. Y.

Huang and J. Y. C. Sun, “Improving the RF Performance

of 0.18-um CMOS with Deep N-Well Implantation,”

IEEE Electron Device Letters, Vol. 22, No. 10, 2001, pp.

481-483.

[3] K. W. Chew, J. Zhang, K. Shao, W. B. Loh, and S. F.

Chu, “Impact of Deep N-Well Implantation on Substrate

Noise Coupling and RF Transistor Performance for Sys-

J. LIU ET AL.

100

tems-on-a-Chip Integration,” Proceeding of the 32nd

European Solid-State Device Research Conference, Bo-

logna, 24-26 September 2002, pp. 251-254.

[4] D. Kosaka, M. Nagata, Y. Hiraoka, I. Imanishi, M. Mae-

da, Y. Murasaka and A. Iwata, “Isolation Strategy

Against Substrate Coupling in CMOS Mixed-Signal/RF

Circuits,” Symposium on VLSI Circuits Digest of Techni-

cal Papers, Kyoto, 16-18 June 2005, pp. 276-279.

[5] J. Kang, D. Yu, Y. Yang and B. Kim, “Highly Linear

0.18-m CMOS Power Amplifier with Deep-N-Well

Structure,” IEEE Journal of Solid-State Circuits, Vol. 41,

No. 5, 2006, pp. 1073-1080.

doi:10.1109/JSSC.2006.874059

[6] S. F. W. M. Hatta and N. Soin, “Performance of the For-

ward-Biased RF LNA with Deep N-Well NMOS Tran-

sistor,” Proceeding of International Conference on Sem-

iconductor Electronics, Johor Bahru, 25-27 November

2008, pp. 465-469.

[7] J. Han and H. Shin, “A Scalable Model for the Substrate

Resistance in Multi-Finger RF MOSFETs,” IEEE MTT-S

International Microwave Symposium Digest, Philadelphia,

8-13 June 2003, pp. 2105-2108.

[8] Y. Cheng and M. Matloubian, “Parameter Extraction of

Accurate and Scaleable Substrate Resistance Components

in RF MOSFETs, ” IEEE Electron Device Letters, Vol. 23,

No. 4, 2002, pp. 221-223. doi:10.1109/55.992845

[9] N. Srirattana, D. Heo, H. M. Park, A. Raghavan, P. E.

Allen and J. Laskar, “A New Analytical Scalable Sub-

strate Network Model for RF MOSFETs,” IEEE MTT-S

Microwave Symposium Digest, Fort Worth, 6-11 June

2004, pp. 699-702.

[10] I. M. Kang, S. J. Jung, T. H. Choi, H. W. Lee, G. Jo, Y. K.

Kim, H. G. Kim and K. M. Choi, “Scalable Model of

Substrate Resistance Components in RF MOSFETs with

Bar-Type Body Contact Considered Layout Dimensions,”

IEEE Electron Device Letters, Vol. 30, No. 4, 2009, pp.

404-406. doi:10.1109/LED.2009.2014085

[11] S. P. Voinigescu, M. Tazlauanu, P. C. Ho and M. T.

Yang, “Direct Extraction Methodology for Geome-

try-Scalable RF-CMOS Models,” International Confer-

ence on Microelectronic Test Structures, Awaji, 22-25

March 2004, pp. 235-240.

[12] S. P. Kao, C. Y. Lee, C. Y. Wang, J. D.-S. Deng, C. C.

Chang and C. H. Kao, “An Analytical Extraction Method

for Scalable Substrate Resistance Model in RF MOS-

FETs,” 2007 International Semiconductor Device Re-

search Symposium, College Park, 12-14 December 2007,

pp. 1-2.

[13] B. Parvais, S. Hu, M. Dehan, A. Mercha and S. Decou-

tere, “An Analytical Extraction Method for Scalable Sub-

strate Resistance Model in RF MOSFETs,” Custom Inte-

grated Circuits Conference, San Jose, 16-19 September

2007, pp. 503-506.

[14] Y. Cheng, M. J. Deen and C. H. Chen, “MOSFET Mod-

eling for RF IC Design,” IEEE Transactions on Electron

Devices, Vol. 52, No. 7, 2005, pp. 1286-1303.

doi:10.1109/TED.2005.850656

[15] M. M. Tabrizi, E. Fathi, M. Fathipour and N. Masoumi,

“Extracting of Substrate Network Resistances in RF

CMOS Transistors,” Topical Meeting on Silicon Mono-

lithic Integrated Circuits in RF Systems, Atlanta, 8-10

September 2004, pp. 219-222.

[16] J. Han, M. Je and H. Shin, “A Simple and Accurate Me-

thod for Extracting Substrate Resistance of RF MOS-

FETs,” IEEE Electron Device Letters, Vol. 23, No. 7,

2002, pp. 434-436.

[17] Y. S. Lin, “An Analysis of Small-Signal Source-Body

Resistance Effect on RF MOSFET for Low-Cost Sys-

tem-on-Chip (SoC) Applications,” IEEE Transactions on

Electron Devices, Vol. 52, No. 7, 2005, pp. 1442-1451.

doi:10.1109/TED.2005.850691

[18] S. C. Rustagi, L. Huailin, S. Jinglin and Z. X. Yong,

“BSIM3 RF Models for MOS Transistors: A Novel

Technique for Substrate Network Extraction,” Proceed-

ing of IEEE International Conference on Microelectronic

Test Structures, Monterey, 17-20 March 2003, pp.

118-123.

[19] U. Mahalingam, S. C. Rustagi and G. S. Samudra, “Di-

rect Extraction of Substrate Network Parameters for RF

MOSFET Modeling Using a Simple Test Structure,”

IEEE Device Letters, Vol. 27, No. 2, 2006, pp. 130-132.

doi:10.1109/LED.2005.863132

Paper Menu >>

Journal Menu >>