Engineering, 2009, 1, 1-54
Published Online June 2009 in SciRes (http://www.SciRP.org/journal/eng/).
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
Embedded Control of LCL Resonant Converter
Analysis, Design, Simulation and
Experimental Results
S. Selvaperumal1, C. Christober Asir Rajan2
1Department of EEE, Mepco Schlenk Engineering College, Sivakasi, India
2Department of EEE, Pondicherry Engineering College, Pondicherry, India
Received April 3, 2009; revised May 19, 2009; accepted May 22, 2009
Abstract
The Objective of this paper is to give more insight into CCM Operation of the LCL Converter to obtain op-
timum design using state-space analysis and to verify the results using PSPICE Simulation for wide variation
in loading conditions. LCL Resonant Full Bridge Converter (RFB) is a new, high performance DC-DC con-
verter. High frequency dc-dc resonant converters are widely used in many space and radar power supplies
owing to their small size and lightweight. The limitations of two element resonant topologies can be over-
come by adding a third reactive element termed as modified series resonant converter (SRC). A three ele-
ment resonant converter capable of driving voltage type load with load independent operation is presented.
We have used embedded based triggering circuit and the embedded ‘C’ Program is checked in Keil Software
and also triggering circuit is simulated in PSPICE Software. To compare the simulated results with hardware
results and designed resonant converter is 200W and the switching frequency is 50 KHz.
Keywords: Continuous Current Mode, High-frequency Link, MOSFET, Zero-Current Switching, Resonant
Converter
1. Introduction
In Converter applications solid-state devices are operated
at very high frequency. So the switching losses are more
than the conduction losses [1] and it becomes a major
cause of poor efficiency of the converter circuit [2,3].
This leads to the search of a converter that can provide
high efficiency [4], lower component stress [5], high
power, high switching frequency, lightweight as well as
low cost and high power operation [6]. In order to keep
the switching power losses low and to reduce the prob-
lem of EMI, the resonant converter is suggested
[7-9].
The resonant converter is a new high performance
DC-DC converter [10]. A resonant converter can be op-
erated either below resonant (leading p.f) mode or above
resonant (lagging p.f) mode. The most popular resonant
converter configuration is series resonant converter
(SRC), parallel resonant converter (PRC) and series par-
allel resonant converter (SPRC). A SRC has high effi-
ciency from full load to very light loads [11,12]. Where
as a PRC has lower efficiency at reduced loads due to
circulating currents [13,14].
The limitations of two element resonant topologies can
be over come by adding a third reactive element, termed
as modified SRC. SRC has voltage regulation problems
in light load conditions [15,16]; to over come this prob-
lem the modified SRC is presented. The LCL-resonant
converter using voltage source type load has nearly load
independent output voltage under some operating condi-
tions [17]. These converters are analyzed by using
state-space approach. Based on this analysis, a simple
design procedure is proposed. Using PSPICE software
simulates the LCL-Resonant Full Bridge Converter. The
proposed results are improved power densities in air
borne applications.

8 S. SELVAPERUMAL ET AL.
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
2. Modified Series Resonant Converter
A Series Resonant Full Bridge Converter (SRC) modi-
fied by adding an inductor in parallel with the trans-
former primary is presented. This configuration is re-
ferred to as an “LCL Resonance Full Bridge Converter”.
A three element (LCL) Resonance Full Bridge Converter
capable of driving voltage type load with load inde-
pendent operation is analyzed. In such a converter has
load independent characteristics, there is no analysis or
design procedure available. It is shown in this project
that these type of converter requires a very narrow range
of frequencies control from full load to very light loads
and can operate with load short circuit while processing
the desirable features of the SRC. The resonance con-
verter operating in the above resonance (lagging power
factor) mode has a number of advantages (e.g. No need
for lossy snubbers and di/dt limiting inductors). There-
fore, the proposed converter configuration in the above
resonance mode, State-space approach is used for the
converter analysis. A modified SRFB Converter with
capacity output filter has been presented.
3. Circuit Description
The resonant tank of this converter consists of three re-
active energy storage elements (LCL) as opposed to the
conventional resonant converter that has only two ele-
ments. The first stage converts a dc voltage to a high
frequency ac voltage. The second stage of the converter
is to convert the ac power to dc power by suitable high
frequency rectifier and filter circuit. Power from the
resonant circuit is taken either through a transformer in
series with the resonant circuit (or) across the capacitor
comprising the resonant circuit as shown in Fig.1. In
both cases the high frequency feature of the link allows
the use of a high frequency transformer to provide volt-
age transformation and ohmic isolation between the dc
source and the load.
In Series Resonant Converter (SRC), the load voltage
can be controlled by varying the switching frequency or
by varying the phase difference between the two inverts
where the switching frequency of each is fixed to the
resonant frequency. The phase domain control scheme is
suitable for wide variation of load condition because the
output voltage is independent of load.
The basic circuit diagram of the full bridge LCL reso-
nant converter with capacitive output filter is shown in
Figure 1.
The major advantages of this series link load SRC is
that the resonating blocks the DC supply voltage and
there is no commutation failure if MOSFET are used as
switches. Moreover, since the dc current is absent in the
primary side of the transformer, there is no possibility of
current balancing. Another advantage of this circuit is
that the device currents are proportional to load current.
This increases the efficiency of the converter at light
loads to some extent because the device losses also de-
crease with the load current. Close to the resonant fre-
quency the load current becomes maximum for a fixed
load resistance. If the load gets short at this condition
very large current would flow through the circuit. This
may damage the switching devices. To make the circuit
short circuit proof, the operating frequency should be
changed.
The filter circuit has some disadvantage. It is a ca-
pacitor input filter and the capacitor must carry large
ripple current. It may be as much as 48% of the load
current. The disadvantage is more severe for large output
current with low voltage. Therefore, this circuit is suit-
able for high voltage low current regulators.
4. State – Space Analysis
4.1. Assumptions in State Space Analysis
The following assumptions are made in the state spare
analysis of the LCL Resonant Full Bridge Converter.
1) The switches, diodes, inductors, and capacitors used
are ideal.
2) The effect of snubber capacitors is neglected.
Figure 1. DC- DC converter employing LCL full bridge operating in CCM.

S. SELVAPERUMAL ET AL. 9
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
Figure 2. Equivalent circuit model of LCL RFBC.
3) Losses in the tank circuit and neglected.
4) Dc supply used is smooth.
5) Only fundamental components of the waveforms
are used in the analysis.
6) Ideal hf transformer with turns ration n =1.
The equivalent circuit shown in Figure 2 is used for
the analysis. The vector space equation for the converter
is:
X = AX + BU (1)
where m and n take values as shown in Table 1 repre-
senting different modes of continuous and discontinuous
conduction.
However, in the discontinuous conduction mode 7, the
converter operates like a simple SRC with resonant fre-
quency, fo and iLs=iLp. It is interesting to note that in all
six continuous conduction modes, the voltage VLP is
clamped and the current iLp is independent of the other
two state variables. As a result, the 3rd order matrix (1)
can be reduced to second order equation for which the
solutions are readily available [2].
The state equation describing period tp-1 < t < tp
mVg = Ls (diLs/dt) + nVo–Vc (2)
(diLs/dt) = (m/Ls)Vg – (nVo/Ls) – (1/Ls)Vc (3)
(dVCs/dt) = (1/Cs) iLs (4)
(diLp/dt) = (nVo/Lp) (5)
State matrix: X = AX + BU





01/ 0//
()
1/00( )00
000() 0/
smss
Ls Lsg
cs scs
o
p
Lp Lp
LLn
iit
V
dVC Vt
dt V
iit
 
  
  
 
  
  
   
L
nL





(6)
Table 1. Different mode of operation.
Mode m n So id
1 +1 +1 ON > 0
2 0 +1 ON > 0
3 -1 +1 ON > 0
4 +1 -1 ON > 0
5 0 -1 ON > 0
6 -1 -1 ON > 0
7 0 - OFF 0
8 +1 - OFF 0
9 -1 - OFF 0
The sum of the zero input response and the zero state
response.
X(t) = [ (t) [X (o) ] ] + L-1 ( (s) B[U (s) ] (7)
The transition matrix
(t) = L-1 [ (S)] (8)
= L-1 [(SI-A) -1] (9)
(S I - A) = S3 + S ώ2
= S (S2 + ώ2) (10)
where ώ=1/√LC

2
2
22
2
2
22
22
/0
/0
00
/0
1/0
()
00
SSC
AdjSIAS LsS
Sώ
SSC
SLs S
SS ώ
Sώ



















22 22
22 22
/1/()
()1/ ()/()0
00
SS ώCs Sώ
SLsSώSS ώ
S


 


 




0
1
11
11 1
cos sin0
() sincos0
00
ώtώtCsώ
tώtLsώώt 







1
 Zero state response, = L-1 [( (s) B [U (s)]]

10 S. SELVAPERUMAL ET AL.
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
22 22
122 22
11
11
1
()/sin(
/1/()0///
1/()/()000[1c o s() ]
0010// /( )
p
p
p
mVgnVo Zosώtt
SS ώCs SώmLsnLsVgS
LLsSώSS ώmVg nVoώtt
SnLpVoS
VoLp tt







 



 









)
p

x(t) = [  (t) [ x(o) ] + L-1 [  (s) B[U (s)] ]
1 1111111
111 11
1
cos()sin()/0 ()()/sin()
()
()sin()/cos1( )0( )[1
() 001()
ppLsp
Ls
cs cs
ppp
Lp Lp p
ώtt tώttLsώittmVgnVo Zosώtt
it
Vt ώtt Csώώ ttVtt mVgnVo
it itt
 



  








 




11
1
cos ()]
/( )
p
p
ώtt
nVoLp tt











I Ls(t) = cos ώ1 (t-tp-1) ILs(tp-1) + (sin ώ 1(t-tp-1) / Ls ώ1) VCs(tp-1)+ ( ( mVg-nVo) / Zos) sin ώ1 (t-tp-1) (11)
I Ls(t) = ILs ( tp-1 ) cos[ώ1(t - tp-1)] + [(mVg – nVo –Vcs (tp-1) / Zos ] sin[ώos(t - tp-1)] (12)
Vcs(t) = iLs (tp-1) Zos sin [ώos ( t - tp-1)] + (m Vg - nVo) [1-cos ώ1(t-tp-1)] + Vcs (tp-1) cos [ώ1(t-tp-1)] (13)
iLp (t) = iLp ( t p-1) + ( n / Lp ) Vo ( t - tp-1 ) (14)
where, tp-1 is the time at the start of any, ccm. tp is the time at the end of the same ccm.
Similarly, the solutions for the discontinuous conduction mode are: iLs = iLp.
iLs(t) = iLp(t) = iLs ( tp-1 ) cos [ώo ( t – t p-1) ] + [(mVg-Vcs (tp-1) / Zo) sin( t - tp-1)] (1 5)
VCs(t) = iLs (t p-1) Zo sin [ώo( t - tp-1)] + mVg[1-cos[ώo(t - tp-1)]] + Vcs(tp-1) cos (ώo (t -t p-1)] (16)
where D is the duty cycle =  / (Ts / 2)
From Mo equation, it can be concluded that the output
voltage is not dependent on the load resistance and con-
verter gain follows a sine function. These results are
completely validated experimentally by plotting the
variation of Mo with duty ratio. At the optimum normal-
ized switching frequency fno, mo is independent of varia-
tions in the load resistance for all pulse widths. The de-
viation increases with reducing values of load resistance
or increasing values of load current for the given voltage.
This arises because of sensing resistance of 0.5  used in
series with the resonant element for monitoring its and
also finite resistance offered by diodes and MOSFET’S
in conduction. In order to maintain the output voltage
constant at desired value against the variations in the
load resistance and supply voltage variations, the pulse
width has to be changed in a closed-loop manner. How-
ever, the required change in pulse width to maintain con-
stant output voltage against load variations and constant
input voltage is very small.
5. Design Procedure
5.1. Design: (Operating Switching Frequency =
50khz)
It is desired to design the converter with the following
specifications:
1) Power output =200W
2) Minimum input voltage =100V
3) Minimum output voltage =125V
4) Maximum load current = 1.6 A
5) Maximum overload current = 4A
6) Inductance ratio (KL) = 1
The hf transformer turns ratio assumed to be unity.
The load resistance:
RL= Maximum output voltage / maximum output current.
= 100 / 1.6
= 62.5
 63
Figure 3. Variation of voltage gain with the duty ratio.

S. SELVAPERUMAL ET AL. 11
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
The input rms voltage to the diode bridge:
0
()22/
Lp
VV

 (17)
The input rms current at the input of the diode bridge
0
[/22]
I
  (18)
The reflected ac resistance on the input side of the di-
ode bridge is
/
acLP d
R
VI (19)

00
/ 22///22
LP d
VI VI  

00
2222 /VI   
0
2
0
/8/
LP d
VIV I

 (20)
For maximum power output
2
/8/s
sL
LC R

 (21)
2
875/


60.8
Since the switching frequency is 50 KHz
3
1/2/5010s
s
LC
60.8
s
s
LC
/60.8ss CL (22)
3
1/2/ 60.85010
ss
LL
3
60.8 /25010
s
L  
from this
1/ 2()
s
Ps
o
f
LLC




 (23)
185
s
L



0.052sCF


From the availability of the capacitors, is in chosen as
0.05μF.The inductance Ls is obtained as 202μH. In the
experimental setup, the actual inductance used is 200μH,
which is close to the designed value.
6. Simulation of LcLResonant Full
Bridge Converter
The simulated circuit of LCL Resonant Full Bridge
Converter is shown in Figure 4.
Power MOSFET, are used as switches M1, M2, M3
and M4 in the converters for an operating frequency of
50KHz. The anti parallel diodes, D1, D2, D3 and D4
connected across the switches are not need because they
have inherent anti-parallel body diodes. The forward
current and the reverse voltage ratings of the diode are
the same as the current and voltage ratings of the MOS-
FET. The internal diode is characterized by forward
voltage drop and reverse recovery parameters like a dis-
crete diode.
The resistor, inductor, capacitors, the power diodes
and the power MOSFET’S are represented by their
PSPICE Model. MOSFET IRF 330 is selected as the
switching device which meets the peak current and volt-
age requirements.
Figure 4. LCL resonant converter circuit.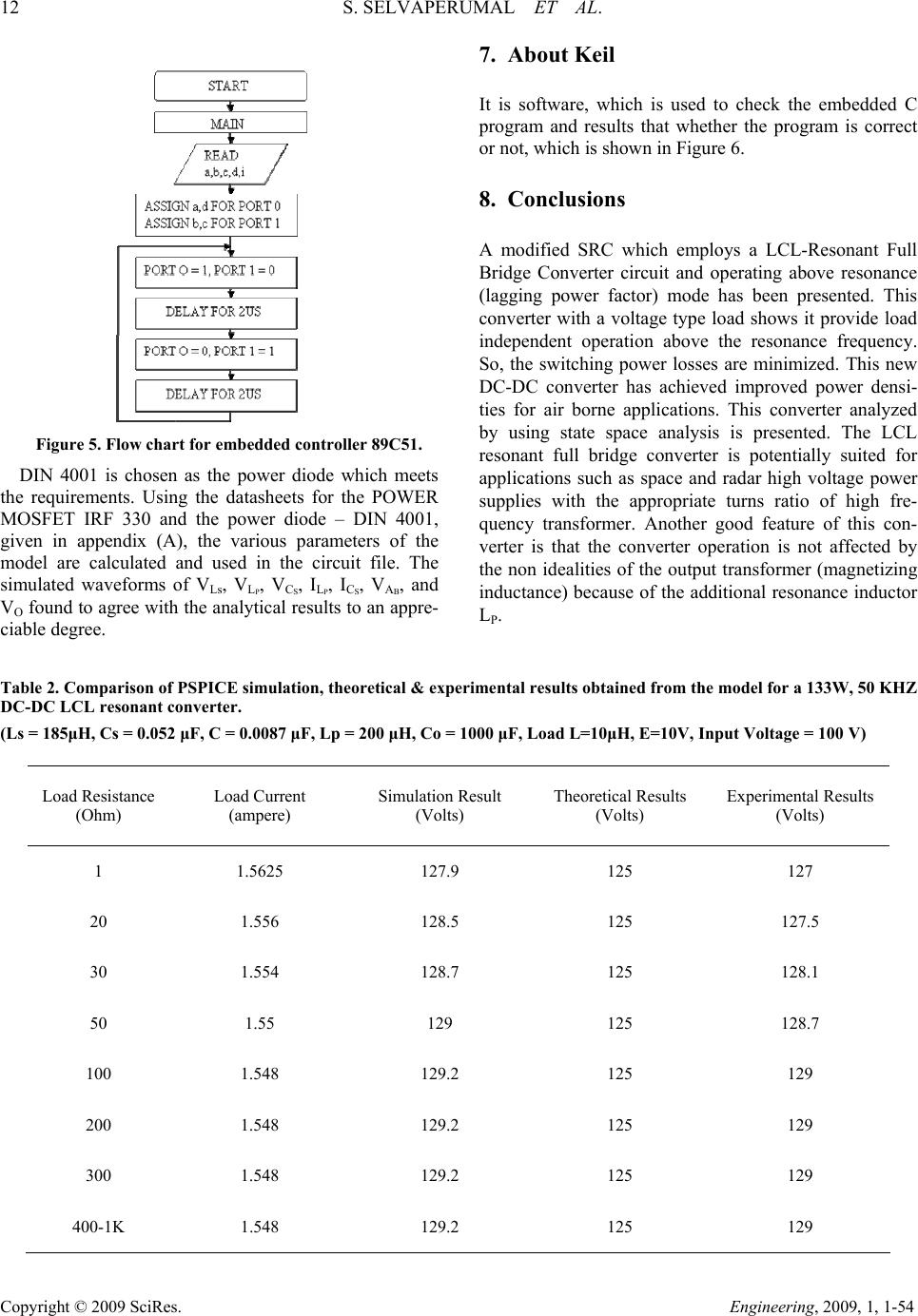

12 S. SELVAPERUMAL ET AL.
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
Figure 5. Flow chart for embedded controller 89C51.
DIN 4001 is chosen as the power diode which meets
the requirements. Using the datasheets for the POWER
MOSFET IRF 330 and the power diode – DIN 4001,
given in appendix (A), the various parameters of the
model are calculated and used in the circuit file. The
simulated waveforms of VLs, VLP, VCS, ILP, ICS, VAB, and
VO found to agree with the analytical results to an appre-
ciable degree.
7. About Keil
It is software, which is used to check the embedded C
program and results that whether the program is correct
or not, which is shown in Figure 6.
8. Conclusions
A modified SRC which employs a LCL-Resonant Full
Bridge Converter circuit and operating above resonance
(lagging power factor) mode has been presented. This
converter with a voltage type load shows it provide load
independent operation above the resonance frequency.
So, the switching power losses are minimized. This new
DC-DC converter has achieved improved power densi-
ties for air borne applications. This converter analyzed
by using state space analysis is presented. The LCL
resonant full bridge converter is potentially suited for
applications such as space and radar high voltage power
supplies with the appropriate turns ratio of high fre-
quency transformer. Another good feature of this con-
verter is that the converter operation is not affected by
the non idealities of the output transformer (magnetizing
inductance) because of the additional resonance inductor
LP.
Table 2. Comparison of PSPICE simulation, theoretical & experimental results obtained from the model for a 133W, 50 KHZ
DC-DC LCL resonant converter.
(Ls = 185μH, Cs = 0.052 μF, C = 0.0087 μF, Lp = 200 μH, Co = 1000 μF, Load L=10μH, E=10V, Input Voltage = 100 V)
Load Resistance
(Ohm)
Load Current
(ampere)
Simulation Result
(Volts)
Theoretical Results
(Volts)
Experimental Results
(Volts)
1 1.5625 127.9 125 127
20 1.556 128.5 125 127.5
30 1.554 128.7 125 128.1
50 1.55 129 125 128.7
100 1.548 129.2 125 129
200 1.548 129.2 125 129
300 1.548 129.2 125 129
400-1K 1.548 129.2 125 129

S. SELVAPERUMAL ET AL. 13
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
From Table 2, it is known that the hardware result for
open loop LCL resonant converter varies from 127 V to
129V. But theoretical result should not go beyond 125V.
So there is a scope for future extension.
The LCL-resonant full bridge converter is simulated
by using PSPICE software. The simulation is carried out
for 120μS which is equivalent to six cycles, and simula-
tion results are obtained. The triggering circuit of
LCL-RFB converter is also simulated by using PSPICE
software. The hardware implementation of triggering
circuit and the power circuit are obtained and the results
are compared to the simulation results.
9. Scope of Future Extension
Analysis, design, simulation and fabrication of closed
loop LCL resonant converter.
Comparison result of open loop and closed loop LCL
resonant converter.
Figure 6. Program result for embedded controller output using Keil software.
Figure 7. Prototype model -embedded control of LCL resonant converter.

14 S. SELVAPERUMAL ET AL.
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
Figure 8. Experimental results of gate voltage (X axis represents time in micro seconds and Y axis represents Gate Voltage.
The amplitude is 5V. If M1 & M4 conduct 0-20µs then M1 & M4 are in OFF State. If M2 & M3 conduct 20µs - 40µs then M2
& M3 are in OFF State).
Figure 9. Experimental results obtained from the model for a 133W, 50 KHZ DC-DC LCL Resonant Converter output volt-
age = 127. 5 V (Ls = 185μH, Cs = 0.052 μF, C = 0.0087 μF, Lp = 200 μH, R= 20Ω, Co = 1000 μF, Load L=10μH, E=10V, Input
Voltage = 100 V).
10. References
[1] A. K. S. Bhat, “Analysis and design of a modified series
resonant converter,” IEEE Transactions, Power Electron-
ics, Vol. 8, pp. 423-430, October 1995.
[2] A. K. S. Bha, “Analysis and design of LCL-Type series
resonant converter,” IEEE INTELEC, pp. 172-178, 1994.
[3] A. K. S. Bhat, “Analysis and design of a fixed-frequency
LCL-Type series resonant converter with capacitive out-
put filter,” IEE PROC-Circuits Devices System, Vol. 144,
No. 2, April 1997.
[4] R. Sevverns, “Topologie for three element resonant con-
verter,” in IEEE Applied Power Electronics, Conference
Record, pp. 712-722, March 1990.
[5] E. G. Schmidtner, “A new High-Frequency resonant
Converter topology,” in High Frequency Power Conver-
sion Conference Record, pp. 390-403, 1988.
[6] R. L. Steigerwald, “A comparison of half bridge resonant
converter topology,” IEEE Transaction, Power Electron-
ics, Vol. 3, pp.174-182, April 1988.
[7] T. H. Solane, “Design of high-efficiency series resonant
converter above resonance,” IEEE Transactions, Aero-
space Electronics System, Vol. 26, pp. 393-402, March
1990.
[8] V. Agarwal, V. Belaguli, and A. K. S. Bhat, “Large sig-
nal analysis using discrete time domain modeling for
LCC-type parallel resonant converter operating in discon-
tinuous current mode,” in Canadian Conference Electrical

S. SELVAPERUMAL ET AL. 15
Copyright © 2009 SciRes. Engineering, 2009, 1, 1-54
and Computer Engineering, pp. 83–88, 1993.
[9] K. S Bhat, “Analysis and design of a series parallel reso-
nant converter,” IEEE Transactions on Power Electronics,
Vol. 8, pp.1–11, 1993.
[10] V. Belaguli, “Series-parallel and parallel series resonant
converters operating on the utility line-analysis, simula-
tion and experimental results,” Ph.D. Dissertation, Uni-
versity Victoria, 1995.
[11] R. Severns, “Topologies for three element resonant con-
verters,” in IEEE Applied Power Electronics, Conference
Record, pp. 712–722, 1990.
[12] H. Neufeld, “Half-bridge resonant converter using the
CS-360,” Cherry Semiconductor, Application Note, 1990.
[13] B. P. McGrath, “Design of a soft-switched 6-kw battery
charger for traction applications,” IEEE Transactions on
Power Electronics, Vol. 22, No. 4, pp.1136–1142, July 2007.
[14] H. Deng, “Analysis and design of iterative learning con-
trol strategies for UPS inverters,” IEEE Transactions on
Industrial Electronics, Vol. 54, No. 3, pp. 1739–1751,
June 2007.
[15] F. Z. Peng, “Z-Source inverter for motor drives,” IEEE
Transactions on Power Electronics, Vol. 20, No. 4,
pp.857–862, July 2005.
[16] V. Belaguli, “Series-parallel and resonant converter oper-
ating in DCM–Analysis, design, simulation and experi-
mental results,” IEEE Transactions on Circuits and Sys-
tems, Vol. 47, pp. 433–441, 2000.
[17] Y. Jang, “Isolated boost converters,” IEEE Transactions
on Power Electronics, Vol. 22, No. 4, pp. 1514–1521,
July 2007.