Paper Menu >>
Journal Menu >>
 Circuits and Systems, 2011, 2, 74-84 doi:10.4236/cs.2011.22012 Published Online April 2011 (http://www.SciRP.org/journal/cs) Copyright © 2011 SciRes. CS A 12-Bit 1-Gsample/s Nyquist Current-Steering DAC in 0.35 µm CMOS for Wireless Transmitter Peiman Aliparast1,2, Hossein B. Bahar2, Ziaadin D. Koozehkanani2, Jafar Sobhi2, Gader Karimian2 1Young Research Club, Islamic AZAD University of Sofian, Sofian, Iran 2Faculty of Electrical and Computer Engineering, University of Tabriz, Tabriz, Iran E-mail: p-aliparast@tabrizu.ac.ir Received December 26, 2010; revised January 25, 2011; accepted March 4, 2011 Abstract The present work deals with 12-bit Nyquist current-steering CMOS digital-to-analog converter (DAC) which is an essential part in baseband section of wireless transmitter circuits. Using oversampling ratio (OSR) for the proposed DAC leads to avoid use of an active analog reconstruction filter. The optimum segmentation (75%) has been used to get the best DNL and reduce glitch energy. This segmentation ratio guarantees the monotonicity. Higher performance is achieved using a new 3-D thermometer decoding method which re- duces the area, power consumption and the number of control signals of the digital section. Using two digital channels in parallel, helps reach 1-GSample/s frequency. Simulation results show that the spurious- free-dynamic-range (SFDR) in Nyquist rate is better than 64 dB for sampling frequency up to 1-GSample/s. The analog voltage supply is 3.3 V while the digital part of the chip operates with only 2.4 V. Total power consumption in Nyquist rate measurement is 144.9 mW. The chip has been processed in a standard 0.35 µm CMOS technology. Active area of chip is 1.37 mm2. Keywords: Wireless Transmitter, 3-D Thermometer Decoding, Current Steering DAC, WLAN, Integrated Circuits, CMOS 1. Introduction The rapid improvement in the field of wireless commu- nications and the image signal processing area requires the designers to put an increasing amount of design effort in the integration of digital and analog systems on a chip (SoC). High performance DACs find applications in the area of wireless transceivers such as Wireless Local Area Networks (WLAN) and Wireless Metropolitan Area Networks (WMAN), image signal processor such as High Definition Television (HDTV), digital signal syn- thesizers, and etc. CMOS current mode DACs are the natural candidate for such applications Because of their high speed, low power, and cost effectiveness [1]. No- wadays the WLAN products are increasing in the market. The WLAN infrastructure such as access points con- nected to the internet exists now everywhere in homes, offices, and public spaces such as WLAN hotspots. New services or applications are being created by connecting various kinds of WLAN products with the WLAN infra- structure. Figure 1 shows the typical structure of a direct conversion (zero-IF) transmission chain for wireless ap- plications. Two DACs are needed to convert the I and Q digital modulated signals coming from the digital signal proces- sor (DSP) into analog waveforms, which are smoothed by the following low-pass reconstruction filters. These base- band signals are then shifted to radio frequency (RF) by two quadrature mixers, and summed up to obtain the final waveform to be transmitted at the antenna, after the am- plification prov ided by the power amplifier (PA) [2]. The baseband sections of such telecom standard transmitters typically consist of cascading of a digital-to-analog con- Figure 1. General block diagram of direct conversion for wireless transmitter chain . I Q  P. ALIPARAST ET AL. Copyright © 2011 SciRes. CS 75 verter (DAC), receiving the digital signal processor (DSP) bit-stream, and an analog reconstruction filter, which has to suppress the DAC spectral images. Digital interpola- tions filter to be situated between the DSP (which typi- cally operates at Nyquist frequency) and the DAC, to enhance the data-rate to the desired value. The design of such a baseband section of wideband wireless communi- cation systems has to optimize the trade-off between two possible approaches: A low DAC conversion frequency, implies a low power in terpolation filter, with demand to a high-order, power-hungry analog reconstruction filter, and a high DAC conversion frequency, implies a digital filter with a high interpolation factor, that relaxes the re- quired performance of the analog smoothing filter. This trade-off is presently optimized with a DAC data-rate about 8-10 times the signal bandwidth and a 4-6th order analog reconstruction filter. For instance, in the case of the WLAN IEEE 802.11a standard (whose signal band- width is equal to 10 MHz), the DAC data-rate is around 100 MHz as illustrated in Figure 2 [2-4]. Due to the upcoming higher data rate standards (IEEE 802.16 and 802.11n, for instance), future implementa- tions will involve with several critical issues on this ba- seband section architecture. As the new standards will present a larger signal bandwidth (25 MHz for the up- coming IEEE 802.16, for instance [5]), the use of tradi- tional transmission (TX) baseband architectures will re- sult in a more and more critical design of the analog fil- ters, since their cut-off frequency has to be increased (with an increasing sensitivity to the lower CMOS gain and to the non-dominant poles) [6]. Figure 3 shows this work which exploits the DAC oversampling ratio (OSR) to avoid the use of an active analog reconstruction filter [2]. As a matter of fact, the DAC conversion frequency is increased up to 1 GHz. 2. High Speed Conventional Current-Steering DACs 2.1. Binary Weighted Architecture VS. Unary Decoded Architecture Current-steering DACs are based on an array of matched current sources which are unity decoded or binary weighted [7]. As shown in Figure 4, the reference source is simply replicated in each branch of the DAC, and each branch current is switched on or off based on the input code. For the binary version, the reference current is multiplied by a power of two, creating larger currents to represent higher-magnitude digital signals. In the unit- element version, each current branch produces an equal amount of current, and thus 2N current source elements are needed. The performance of the DAC is specified through static parameters: Integral Non-Linearity (INL), Differential Non-Linearity (DNL) and parametric yield; and dynamic parameters: glitch energy, settling time and SFDR [8]. Static performance is mainly dominated by systematic and random errors. Systematic errors caused by process, temperature and electrical slow variation gradients are almost cancelled by proper layout tech- niques [9]. Random errors are determined solely by mismatch due to fast variation gradients. Advantages and disadvantages of these structures are Figure 2. Traditional baseband analog section for wireless transmitters. Figure 3. This work which exploits impact of the DAC conversion frequency on the filter implementation.  P. ALIPARAST ET AL. Copyright © 2011 SciRes. CS 76 Figure 4. (a) Unit-element current-steering DAC; (b) Bi- nary current-steering DAC. summarized below: Thermometer: Advantages Low glitch energy Monotonicity Small DNL errors Disadvantages Digital decoding with more area and power consumption Increased number of control signals Binary: Advantages Low digital power consumption Small number of control signals Disadvantages Monotonicity not guaranteed Larger DNL errors Large glitch energy Figure 5 also summarizes aforementioned points graphically. 2.2. Segmented DAC Structure Usually, to leverage the clear advantages of the ther- mometer-coded architecture and to obtain a small area simultaneously, a compromise is found by using seg- mentation [10]. The DAC is divided into two sub-DACs, one for the MSBs and one for the LSBs. Thermometer coding is used in the MSB where the accuracy is needed mostly. Because of the reduced number of bits in this section, the size is considerably smaller than a true ther- mometer coded design. The LSB section can either be done using the binary-weighted or the thermome- ter-coded approach. We will refer to a fully bi- nary-weighted design as 0% segmented, whereas a fully thermometer-coded design is referred to as 100% seg- mented. The design of current-steering DAC starts with an architectural selection to find the optimum segmenta- tion ratio (m over n) that minimizes the overall digital and analog area [10-12]. The INL is independent of the segmentation ratio and depends only on the mis- match if the output impedance is made large en ough [7]. Figure 5. Binary weighted versus Unary-decoded. The DNL speciation depends on the segmentation ratio but it is always satisfied provided that the INL is below 0.5 LSB for reasonable segmentation ratios. The glitch energy is determined by the number of binary bits b, be- ing the optimum architecture in th is sense a totally unary DAC. However, this is unfeasible in practice due to the large area and delay that the thermometer decoder would exhibit. The minimization of the glitch energy is then done in circuit level design and layout of the switch and latch array and current source cell [13].The optimum segmentation is workout 75% in [10,12] so we have used this segmentation to achieve the best performance in high-speed design. Thus we consider 9-bit as thermome- ter-coded and 3-bit as binary-weighted. Figure 6 shows a typical block diagram of an n-bit segmented cur- rent-steering DAC which uses the advantages of both architectures. Input word is segmented between b less significant bits that switch a binary weighted array and m= n – b most significant bits that control switching of a unary current source array. The m input bits are ther- mometer decoded to switch individually each of the un- ary sources [14-16]. A dummy decoder is placed in the binary weighted input path to equalize the delay. A latch is placed just before the switch transistors of each current source to minimize any timing error [10]. 3. New Thermometer Decoding Arch it ec t ur e Figure 7 shows a block diagram of a conventional row and column decoded 12-b it current-steer ing DAC. In this  P. ALIPARAST ET AL. Copyright © 2011 SciRes. CS 77 Figure 6. A typical segmented current-steering DAC archi- tecture. Figure 7. Block diagram of a conventional row and column decoded 12-bit current-steering DAC. block diagram, the lower significant bits are applied to a dummy decoder [17]. This decoder creates a delay pro- portional to the Binary-to-Thermometer decoder and causes the signal to arrive at the switches synchro nously. The f ive L SB b its are colu mn de coded an d the f our MSB bits are row decoded. Column decoder is a 5-input 31-output Binary-to-Thermometer Decoder and row de- coder is a 4-input 15-output Binary-to-Thermometer Decoder. Outputs of the decoders control 511 current cells in the main matrix. But if we think about Bi- nary-to-Thermometer Decoder structure we understand that β-bit increase of the input of the decoder cause the area, complexity, number of control signal and power consumption of the decoder increase with 2β. In fact power and area are doubled with only one bit increase in the input of the decoder and we can write: 4to15BTD 23to7BTDP P (1) 4to15 BTD23to7BTDA A (2) Thus: 5to 31 BTD43to7 BTDP P (3) 5to31BTD43to7 BTDA A (4) where BTD is Binary-to-Thermometer Decoder, P is the power consumption of the decoder and A is active area that the decoder uses. Now consider Figure 8 that shows a 3D decoding architecture. In this block diagram three BTD have been used. Three bits for height, three bits for row and three bits for column and every cell is selected with 3 parameters (R, C and H). In fact we have only used three (3to7 BTD) instead of two (5to31 BTD) and (4to15 BTD) thus power consumption and area of the circuit have been improved two times because: 4to15 BTD23to7 BTDP P + 5to31BTD 43to7BTDP P 4to15BTD5to31 BTD63to7BTDP P P (5) And for area we have: 4to15BTD 23to7BTDA A + 5to31BTD43to7BTDA A 4to15BTD5to31 BTD63to7BTDA A A (6) In this structure 3 LSB bits are column decoded, 3 middle bits are row decoded and 3 MSB bits are height decoded. On the other hand, we have only used 21 con- trol signals instead of 46 control signals thus the number of control signals has been decreased by 55 percent hence we can achieve the best speed and performance. 4. The Current Cell, Latch and Driver Static and dynamic performance of current-steering Figure 8. Block diagram of a novel method row and column and height decoded 12-bit 3-D DAC. I out+ I out– I out+ I out–  P. ALIPARAST ET AL. Copyright © 2011 SciRes. CS 78 DACs is mostly determined by the accuracy of the cur- rent sources, finite output impedance, and switching time. Figure 9 shows a current source transistor MCS, an addi- tional cascode transistor MCAS that increases the output impedance and two complementary switch transistors MSW. This figure shows cascode current source and switch structure for 1LSB while for realizing unary cur- rent source cell (8LSB) we used same structure with 8 parallel transistors. In proposed 12-bit DAC three bits are binary weighted so it uses the current source of Figure 9 and remaining 9 bits are thermometer decoded and need unary current sources. Since two D/A converters pro- cessed in the same technology do not necessarily have the same specifications due to technological variations, therefore it is of the utmost importance to know th e rela- tionship that exists between the specifications of the cir- cuit and the matching properties of used technology. For a current-steering D/A converter, the INL is mainly de- termined by the matching behavior of the current sources. A parameter that is well suited for expressing this tech- nology versus DAC specification relation is the INL yield [16]. This INL yield is defined as the ratio of the number of D/A converters with an INL smaller than 1 LSB to the total number of tested D/A converters. As defined by Pelgrom, mismatch “is the process that causes time- independent random variations in physical quanti- ties of identically designed devices” [18]. Pelgrom’s pa- per has become the de facto standard for analysis of tran- sistor matching, and thus his formula for the standard deviation of saturation current for two identically sized devices has been used for the design. This formula is: 222 222 4T GS T IV IVV (7) where Figure 9. Current source cell topology. 2 222 VT TVT A VSD WL (8) and 2 222 2 ASD WL (9) Most of these variables are process-dependent con- stants. Using these results, an equation for the minimum size device that still provides a reasonable current stan- dard deviation can be determined [13]: 2 22 22 4 1 2 VT cs minGS T A IA WL IVV (10) where Aβ, AVT , VGS and VT are process parameters, while I is the current generated by a given source and σI is the relative standard deviation of one current source. The same aspect ratio can be obtained for different areas W×L, except for the MCS transistor, because the usual INL-mismatch specification eliminates one degree of freedom. The relative standard deviation of a unit current source σI/I has to be small enough to fulfil the INL< 0.5 LSB specification given a parametric yield [17]: 2 21 05 2 2 upper bound N INL I yield Iinv _ normal.. (11) where inv_normal is the inverse cumulative normal dis- tribution. The MCS transistor size is found by: 22 2 22 4 4VT nox AA I WVV I CI (12) 2222 24 4 nox VT C LA.VA I I. I (13) where µnCOX is the MOS transistor gain factor and ΔV = (VGS – VT ). Applying Equations (12) and (13) we arrived in Wmin = 4 µm and Lmin = 5 µm for the current source. But in design of cascode current sources, to achieve high speed, we need to choose the size of cascode transistor as small as possible. With different size for WCAS and WCS, we have to use contact in node Y (Figure 9) which in- creases parasitic capacitance and decreases the speed . So in a trade off, we decided to decrease WCS as small as possible and use the same size with WCAS. In other words we have chosen WCAS = WCS = 2 µm, and avoid using contact in node Y. To compensate for reduction in WCS in Equation (14), we increase the values of LCS (LCS = 10 µm) and ΔV while we keep LCAS at its minimum size 0.35 µm. Thus we do not use these Equations (12) and (13) and use only mismatch Equation (10) to reach a  P. ALIPARAST ET AL. Copyright © 2011 SciRes. CS 79 minimum sizing of current cell. With this method, the speed of switch is high also INL < 0.5 LSB is satisfied. The small-signal output impedance for the current source topology of Figure 9 is given by: outSWCAS dsSWdsCAS dsCS Rgm .gm.r.r.r (14) The optimum MSW and MCAS gate bias voltages con- cerning the output impedance are found by differentiat- ing Rout with respect to VgSW and VgCAS. For the SW and CAS gate bias voltages that maximize output impedance are found as: 122 3 gCASTo minCSCASSW VVVVV V (15) 12 3 gSWTo minCSCASSW VVVVV V (16) Figure 10 shows the biasing scheme for the cascoded current sources. The PMOS sections of the biasing cir- cuits are labeled as Global biasing while the NMOS sections are labeled as Local biasing. In the actual im- plementation, the global biasing is realized using a common-centroid layout to reduce effects of gradients. The local biasing is separated into four quadrants. There is no direct connection between any two quadrants. This will improve both DNL as well as INL performance [10]. A driver circuit with a reduced swing placed between the latch and the switch reduces the clock feed-through to the output node as well [19,20]. Figure 11(a) shows a current source, switch, latch and driver cell. A new swing-reduced-device (SRD) circuit is designed (shown in Figure 11(b) ). The latch circu it co mplemen tary outpu t levels and non-symmetrical cross point are designed to minimize glitches [13]. The waveforms of the different nodes are shown in Figure 11(c) without SRD circuit and Figure 11(d) with SRD circuit. Signals with sym- metrical crossing point are fed from the left and SRD makes a non-symmetrical crossing point which reduces the spike at node VX considerably. In SRD circuit, MSRD1 is always on and when MSRD2 is off, VgSW approaches 2.4 V (power supply value of digital part). When MSRD2 is on with proper sizing of MSRD2, VgSW can be set to de- sired value because VgSW in this case will be equal to VSG of MSRD2 transistors. In this circuit for complete switch- ing of MSW transistors we need 350 mV differential volt- age, so VSG of MSRD2 is set to 2.05 V. On the other hand for non-symmetric crossing it’s enough to choose bigger size for MSRD1 than MSRD2. Size of MSRD1 and MSRD2 has been given in Table 1, also SRD output wave forms and its effect in reducing spike in node VX is shown in Figure 11(d). The capacitive coupling to the analog output is minimized by limiting the amplitude of the control sig- nals just high enough to switch the tail current com- pletely to the desired output branch of the differential Figure 10. Biasing scheme for current sources. pair. In addition the switch transistors are kept relatively small in order to avoid large parasitic capacitances. Table 1. Current source and SRD transistors dimensions and currents. Transistor Size ID MCS W = 2 µm, L = 10 µm 5 µA MCAS W = 2 µm, L = 0.35 µm 5 µA MSW W = 0.5 µm, L = 0.35 µm - MSRD1 W = 1.5 µm, L = 2 µm - MSRD2 W = 1 µm, L = 2 µm - 5. Layout and a Few Techniques to Achieve High Speed Clock distribution for 1 GHz is very difficult and getting data in this speed is very hard thus we have used 2 chan- nels for digital section. Every channel works at 500MHz and then results of two channels are combined at the in- put of the switch to get 1 GHz. Figure 12 shows the structure used for digital section of the DAC. Channel 1 samples input data with clock and channel 2 samples input data with clock-not. A buffer just before switch combines the output of two digital channels. It sends the output of digital channel 1 with clock and the output of digital channel 2 with clock-no t to the input of switch. In fact in one period of clock we take 2 samples of the input code and at the output it seems that the circuit works at 1 GHz. On the other hand, we use master-slave operation in all digital circuits and use pipelining scheme, so in overall the digital circuit only senses one gate-delay. For example the structure of one of 3-input 7-output Bi- nary-to-Thermometer Decoder has been shown in Figure 13. Layout of all digital section has been done manually to guarantee the best speed, low power and minimum area. Figure 14 shows the complete layout of the DAC, latches and switches which are grouped in a separated 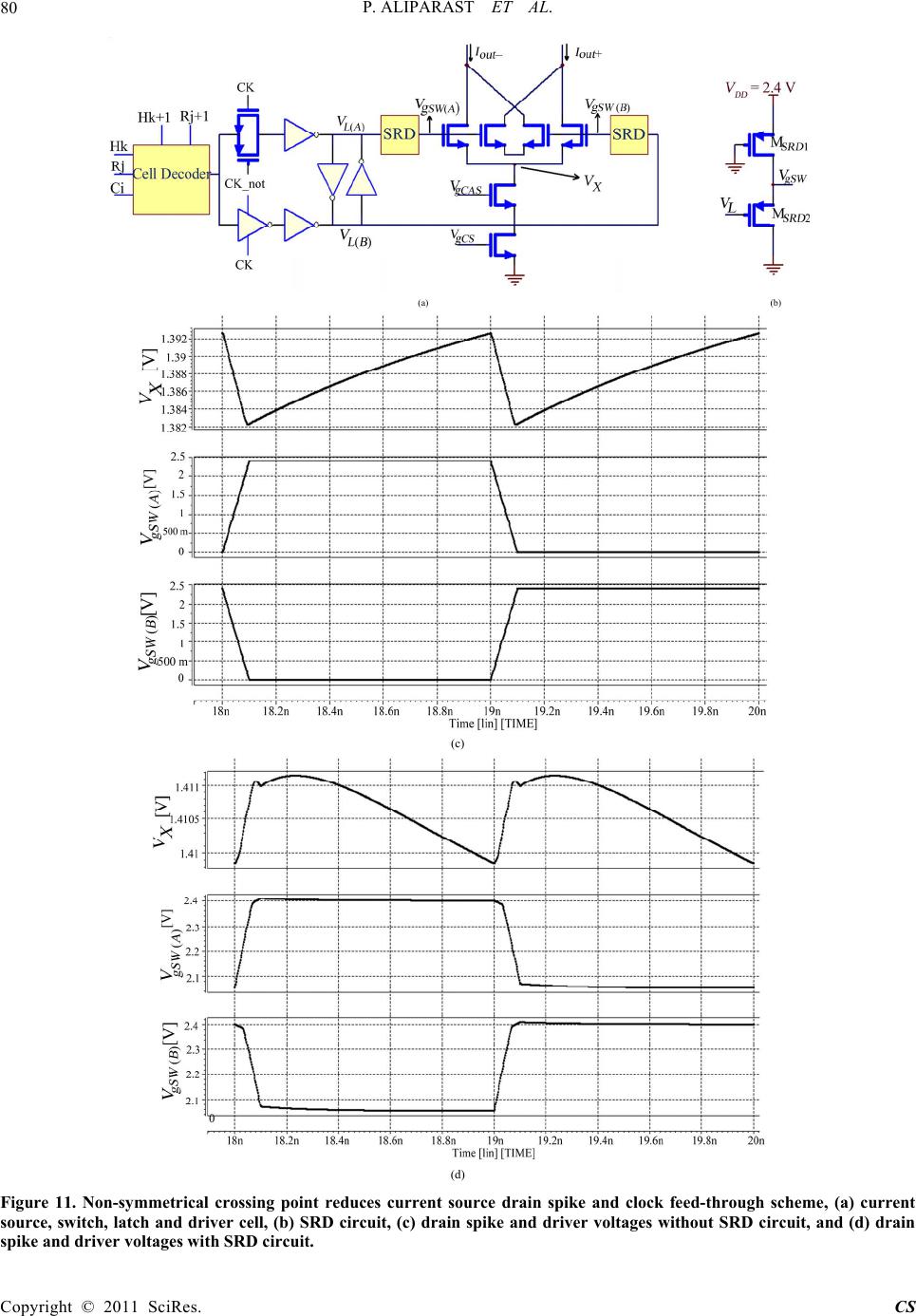 P. ALIPARAST ET AL. Copyright © 2011 SciRes. CS 80 (a) (b) (c) (d) Figure 11. Non-symmetrical crossing point reduces current source drain spike and clock feed-through scheme, (a) current source, switch, latch and driver cell, (b) SRD circuit, (c) drain spike and driver voltages without SRD circuit, and (d) drain spike and driver voltages with SRD circuit. 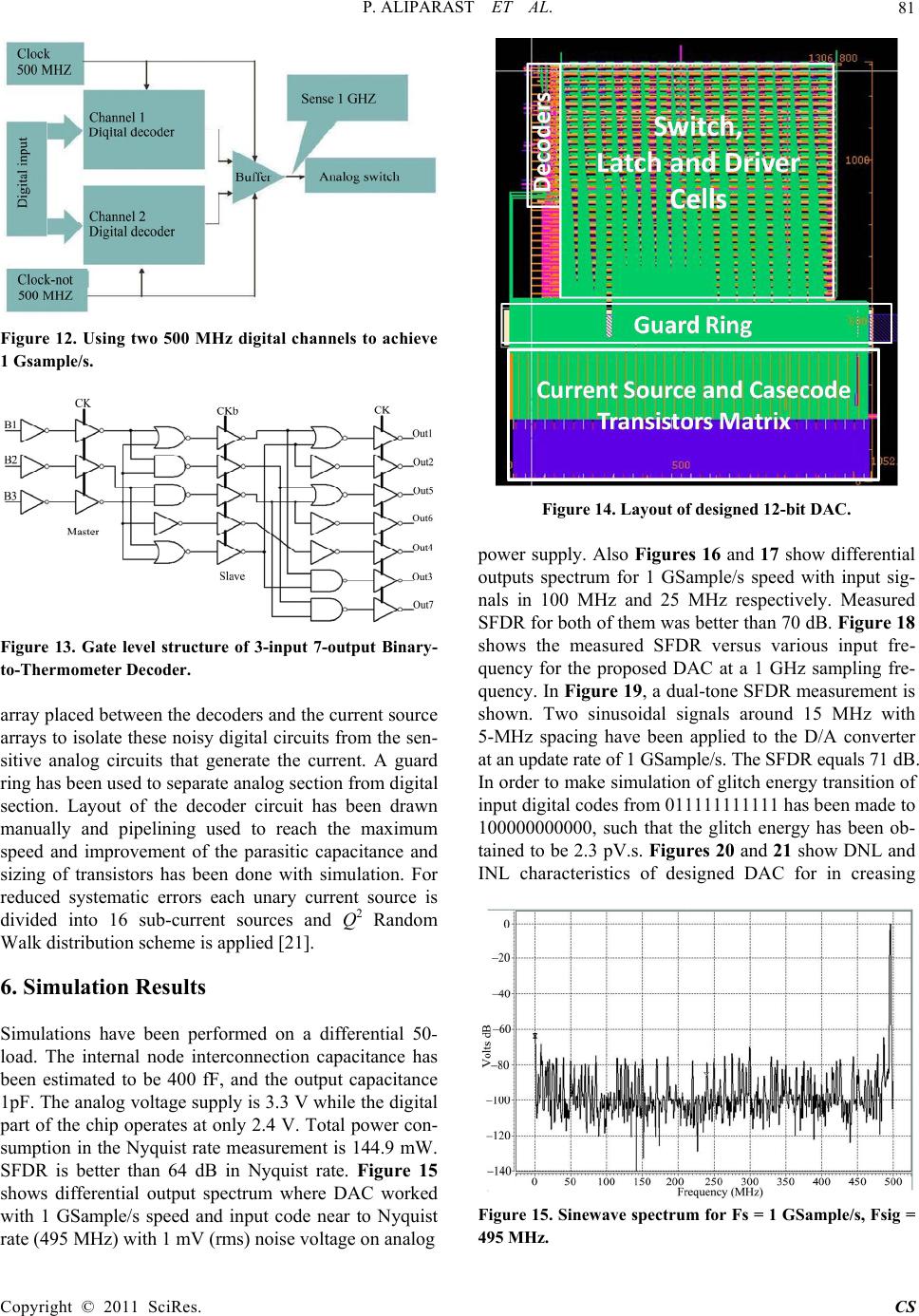 P. ALIPARAST ET AL. Copyright © 2011 SciRes. CS 81 Figure 12. Using two 500 MHz digital channels to achieve 1 Gsample/s. Figure 13. Gate level structure of 3-input 7-output Binary- to-Thermometer Decoder. array placed between the decoders and the current source arrays to isolate these noisy digital circuits fro m the sen- sitive analog circuits that generate the current. A guard ring has been used to separate analog section from digital section. Layout of the decoder circuit has been drawn manually and pipelining used to reach the maximum speed and improvement of the parasitic capacitance and sizing of transistors has been done with simulation. For reduced systematic errors each unary current source is divided into 16 sub-current sources and Q2 Random Walk distribution scheme is applied [21]. 6. Simulation Results Simulations have been performed on a differential 50- load. The internal node interconnection capacitance has been estimated to be 400 fF, and the output capacitance 1pF. The analog vo ltage supply is 3.3 V while the digital part of the chip operates at only 2.4 V. Total power con- sumption in the Nyquist rate measurement is 144.9 mW. SFDR is better than 64 dB in Nyquist rate. Figure 15 shows differential output spectrum where DAC worked with 1 GSample/s speed and input code near to Nyquist rate (495 MHz) with 1 mV (rms) noise voltage on analog Figure 14. Layout of designed 12-bit DAC. power supply. Also Figures 16 and 17 show differential outputs spectrum for 1 GSample/s speed with input sig- nals in 100 MHz and 25 MHz respectively. Measured SFDR for both of them was better than 70 dB. Figure 18 shows the measured SFDR versus various input fre- quency for the proposed DAC at a 1 GHz sampling fre- quency. In Figure 19, a dual-tone SFDR measurement is shown. Two sinusoidal signals around 15 MHz with 5-MHz spacing have been applied to the D/A converter at an update rate of 1 GSample/s. The SFDR equals 71 dB. In order to make simulation of glitch energy transitio n of input digital codes from 01111111 1111 has been made to 100000000000, such that the glitch energy has been ob- tained to be 2 .3 pV.s. Figures 20 and 21 show DNL and INL characteristics of designed DAC for in creasing Figure 15. Sinewave spectrum for Fs = 1 GSample/s, Fsig = 495 MHz.  P. ALIPARAST ET AL. Copyright © 2011 SciRes. CS 82 Figure 16. Sinewave spectrum for Fs = 1 GSample/s, Fsig = 100 MHz. Figure 17. Sinewave spectrum for Fs = 1 GSample/s, Fsig = 25 MHz. input code from 0 to 4096. The INL and DNL obtained from post layout four corners Monte-Carlo simulations considering process mismatch parameters are better than 0.74 LSB and 0.49 LSB, respectively. Table 2 Table 2. Performance summary. Technology 0.35 µm (1P4M) TSMC Mixed Mode CMOS Resolution 12-bit Update rate Up to 1 GS/s Max. output swing 2Vpp diff. DNL Better than 0.49LSB INL Better than 0.74LSB SFDR (495 MHz@1 GS/s) 64 dB SFDR (100 MHz@1 GS/s) 70 dB SFDR (25 MHz@1 GS/s) 71 dB SFDR (1 MHz@1 GS/s) 72 dB ENOB (25 MHz@1 GS/s) 10.7-bit ENOB (1 MHz@1 GS/s) 11-bit Analog Power consumption (at 1 GS/s) 69.3 mW (21 mA from 3.3 V) Digital Power consumption (at 1 GS/s) 75.6 mW (31.5 mA from 2.4 V) Total Power consumption (at 1 GS/s) 144.9 mW Analog/Digital voltage supply 3.3 V/2.4 V Active area 1 306 µm×1052 µm Figure 18. SFDR versus input frequency for the proposed DAC at 1 GHz sampling frequency. Figure 19. Simulated dual-tone spectrum for Fs = 1 GSample/s, Fsig = 20 MHz and 10MHz. Figure 20. DAC INL characteristic. summarizes some of important performance parameters of the DAC. 7. Conclusion In this article a 3.3 V, 12-bit, current-steering, 9 + 3 seg-  P. ALIPARAST ET AL. Copyright © 2011 SciRes. CS 83 Figure 21. DAC DNL characteristic. mented architecture digital to analog converter for base-band of wireless transmitter circuits has been pre- sented. A new 3-D thermometer decoding scheme has been used in digital section which reduces the area power consumption and number of control signals considerably. Simulations have been performed to analyze and solve some of important dynamic linearity limitations. Using two digital channels in parallel, one operating with clock and the other operating with clock-not for the sampling rate of 1 GS/s while each channel operates only at 500 MHz. This clocking strategy makes clock distribution much easier. Analog switches and SRD circuits have been op- timized not only to get minimum area and maximum speed but also to improve dynamic behavior of the DAC. Segmentation (75%) decreases DNL error and glitch energy considerably and guarantees needed improvement of SFDR. Separate power supplies have been used for digital and analog parts. Digital section operates at lower supply voltage than an alog p art. This increases speed and reduces power consumption of the digital part and at the same time decreases power supply noise and improve the performance of the analog part. The technology used is a 0.35 µm, single-poly four-metal, 3.3 V, standard TSMC Mixed Mode CMOS process. The active area of the DAC, as shown in Figure 14, is 1052 µm × 1306 µm. 8. References [1] S. M. Ha, T. K. Nam and K. S. Yoon, “An I/Q Channel 12-bit 120 Ms/s CMOS DAC with Three Stage Ther- mometer Decoders for WLAN,” Proceedings of the IEEE Asia Pacific Conference on Circuits and Systems, Singa- pore, 4-7 December 2006, pp. 355-358. doi:10.1109/APCCAS.2006.342443 [2] N. Ghittori, et al., “1.2-V Low-Power Multi-Mode Dac+Filter Blocks for Reconfigurable (WLAN/UMTS, WLAN/Bluetooth) Transmitters,” IEEE Journal of Solid- State Circuits, Vol. 41, No. 9, 2006, pp. 1970-1982. doi:10.1109/JSSC.2006.880602 [3] S. Khorram, et al., “A Fully Integrated SOC for 802.11 b in 0.18 µm CMOS,” IEEE Journal of Solid-State Circuits, Vol. 40, No. 12, 2005, pp. 2492-2501. doi:10.1109/JSSC.2005.857419 [4] S. Mehta, et al., “An 802.11 g WLAN SOC,” IEEE Journal of Solid-State Circuits, Vol. 40, No. 12, 2005, pp. 2483-2491. doi:10.1109/JSSC.2005.857418 [5] C. Eklund, R. Marks, K. Stanwood and S. Wang, “IEEE Standard 802.16: A Technical Overview of the Wireless Man Air Interface for Broadband Wireless Ac ce ss,” IEEE Communications Magazine, Vol. 40, No. 6, 2002, pp. 98-107. doi:10.1109/MCOM.2002.1007415 [6] N. Ghittori, et al., “An IEEE 802.11 and 802.16 WLAN Wireless Transmitter Baseband Architecture with a 1.2-V, 600-Ms/s, 2.4-mW DAC,” Analog Integrated Circuits and Signal Processing, Vol. 59, No. 3, 2009, pp. 231-242. doi:10.1007/s10470-008-9262-x [7] B. Razavi, “Principles of Data Conversion Systems,” Wiley-IEEE Press, New Jersey, 1995. [8] P. Hendriks, “Specifying Communication DACs,” IEEE Spectrum, Vol. 34, No. 7, 1997, pp. 58-69. doi:10.1109/MSPEC.1997.609817 [9] Y. Cong and R. Geiger, “Switching Sequence Optimiza- tion for Gradient Error Compensation in Thermome- ter-Decoded DAC Arrays,” IEEE Transaction on Circuits and Systems-II, Vol. 47, No. 7, 2000, pp. 585-595. doi:10.1109/82.850417 [10] C. Lin.and K. Bult, “A 10-bit, 500-Ms/s CMOS DAC in 0.6 mm2,” IEEE Journal of Solid-State Circuits, Vol. 33, No. 12, 1998, pp. 1948-1958. doi:10.1109/4.735535 [11] J. Vandenbussche, et al., “Systematic de Sign of High-Accuracy Current-Steering D/A Converter Macro Cells for Integrated VLSI Systems,” IEEE Transaction on Circuits and Systems II: Analog and Digital Signal Processing, Vol. 48, No. 3, 2001, pp. 300-309. doi:10.1109/82.924073 [12] J. Gonzalez and E. Alarcon, “Clock-Jitter Induced Distor- tion in High-Speed CMOS Switched-Current Segmented Digital to Analog Converters,” International Symposium on Circuits and Systems (ISCAS’01), Sydney, 6-9 May 2001, pp. 1512-1515. [13] J. Bastos, M. Steyaert and W. Sansen, “A High Yield 12-Bit 250-Ms/s CMOS D/A Converter,” IEEE Custom Integrated Circuits Conference (CICC), San Diego, 5-8 May 1996, pp. 431-434. [14] L. Sumanen, M. Waltari and K. Halonen, “A 10-Bit High-Speed Low-Power CMOS D/A Converter in 0.2 mm2,” IEEE International Conference on Electronics, Circuits and Systems, Lisboan, 7-10 September 1998, pp. 15-18. [15] Y. Nakamura, T. Miki, A. Maeda, H. Kondoh and N. Yazwa, “A 10-b 70-Ms/s CMOS D/A Converter,” IEEE Journal of Solid-State Circuits, Vol. 26, No. 4, 1991, pp. 637-642. doi:10.1109/4.75066 [16] M. Albiol, J. Gonzalez and E. Alarcon, “Mismatch and Dynamic Modeling of Current Sources in Current-Steer- ing CMOS D/A Converters: An Extended Design Proce- dure,” IEEE Transactions on Circuits and Systems I: Regular Papers, Vol. 51, No. 1, 2004, pp. 159-169. doi:10.1109/TCSI.2003.821287  P. ALIPARAST ET AL. Copyright © 2011 SciRes. CS 84 [17] A. Bosch, M. Borremans, M. Steyaert and W. Sansen, “A 10-Bit 1-Gs/s Nyquist Current Steering CMOS D/A Converter,” IEEE Journal of Solid-State Circuits, Vol. 36, No. 3, 2001, pp. 315-324. doi:10.1109/4.910469 [18] M. Pelgrom, A. Duinmaijer and A. Welbers, “Matching Properties of MOS Transistors,” IEEE Journal of Sol- id-State Circuits, Vol. 24, No. 5, 1989, pp. 1433-1440. doi:10.1109/JSSC.1989.572629 [19] H. Kohno, et al., “A 350-Ms/s 3.3V 8-Bit CMOS D/A Converter Using a Delayed Driving Scheme,” IEEE Cus- tom Integrated Circuits Conference (CICC), Santa Clara, 1-4 May 1995, pp. 211-214. [20] L. Luh, J. Choma, J. Draper, “ A High-Speed Fully Dif- ferential Current Switch,” IEEE Transactions on Circuits and Systems-II: Analog and Digital Signal Processing, Vol. 47, No. 4, 2000, pp. 358-363. doi:10.1109/82.839672 [21] G. Van der Plas, et al., “A 14-Bit Intrinsic Accuracy Q2 Random Walk CMOS DAC,” IEEE Journal of Solid- State Circuits, Vol. 34, No. 12, 1999, pp. 1708-1718. doi:10.1109/4.808896 |

