Descriptively probabilistic relationship between mutated primary structure of von Hippel-Lindau protein and its clinical outcome

doi:10.4236/jbise.2009.23032

Paper Menu >>

Journal Menu >>

J. Biomedical Science and Engineering, 2009, 2, 190-199

Published Online June 2009 in SciRes. http://www.scirp.org/journal/jbise

JBiSE

Descriptively pr obabilisti c relations hip betwee n muta ted

primary structure of von Hippel-Lindau protein and its

clinical outcome

Shao-Min Yan1, Guang Wu2*

1National Engineering Research Center for Non-food Biorefinery, Guangxi Academy of Sciences, 98 Daling Road, Nanning, Guangxi

Province, CN-530007, China; 2Computational Mutation Project, DreamSciTech Consulting, 301, Building 12, Nanyou A-zone, Jianna n

Road, Shenzhen, Guangdong Province CN-518054, China; *Corresponding author (hongguanglishibahao@yahoo.com), Tel: +86 771

2503 930, Fax: +86 755 2664 8177.

Received 5 August 2008; revised 4 January 2009; accepted 7 January 2009.

ABSTRACT

In this study, we use the cross-impact analysis

to build a descriptively probabilistic relationship

between mutant von Hippel-Lindau protein and

its clinical outcome after quantifying mutant

von Hippel-Lindau proteins with the amino-acid

distribution probability, then we use the Bayes-

ian equation to determine the probability that

the von Hippel-Lindau disease occurs under a

mutation, and finally we attempt to distinguish

the classifications of clinical outcomes as well

as the endocrine and nonendocrine neoplasia

induced by mutations of von Hippel-Lindau

protein. The results show that a patient has 9/10

chance of being von Hippel-Lindau disease

when a new mutation occurs in von Hippel-

Lindau protein, the possible distinguishing of

classifications of clinical outcomes using mod-

eling, and the explanation of the endocrine and

nonendocrine neoplasia in modeling v iew.

Keywor ds: Amino Acid; Bayes’ Law; Cross-Impact

Analysis; Distribution Probability; Mutation; Von

Hippel-Lin d au Disease

1. INTRODUCTION

Perhaps, the first step to study the genotype-phenotype

relationship is to determine a protein in relation to a dis-

ease, and the second step would be to build a quantitative

relationship between mutant protein and its clinical out-

come. Then we ma y be in the position to predict the clini-

cal outcome based on such a quantitative relati onship, even

to predict new functions led by new mutations.

Thus, we need the methods, which can quantify a pro-

tein sequence as a numeric sequence in order to build a

quantitative relationship. In fact, we have various ways

to quantify a protein sequence, for example, to use the

physicochemical property of amino acid to quantify a

protein sequence [1].

Since 1999, we have developed three approaches to

quantify each amino acid in a protein as well as a whole

protein (for reviews, see [2,3,4]), and our quantifications

indeed differ before and after mutation, thus it is possi-

ble to use our approaches to build a quantitative rela-

tionship between changed primary structure and changed

functio n of protein.

In 1911 and 1926, von Hippel and Lindau described

the von Hippel-Lindau disease [5,6], later on Melmon

and Rosen established the notion of the von Hippel-

Lindau disease [7], which is an autosomal dominant dis-

order characterized by cerebellar, spinal cord, and retinal

hemangioblastomas; cysts of the kidney, pancreas, liver,

and epididymis; and has an increased frequency of renal

cancer (renal cell carcinoma or hypernephroma), pan-

creatic cancer, and pheochromocytoma [8,9,10]. The von

Hippel-Lindau disease has a birth incidence of about 1 in

36000 and about 20% of cases arise as de novo muta-

tions without a family history [11,12].

The von Hippel -Li ndau disease tum or supp ressor gene

was identified in 1993 [13], of which mutations are the

major cause for developing the von Hippel-Lindau dis-

ease. Pathologically relevant is inactivation of the von

Hippel-Lindau gene and subsequent loss of the function

of the von Hippel-Lindau protein, and Elongin B, C

complex [14,15]. The dysfunction of the ubiquitination

of hypoxia-inducible factors is an important step in the

development of various tumors [15,16,17,18,19]. Also, a

recent study elucidated the role of NGF/JunB/ EglN3-

related pathways in developmental apoptosis linking to

tumourigenesis [2 0].

Clinically the von Hippel-Lindau disease is classified

into two types: type I without pheochromocytoma and

type II with pheochromocytoma [10,17]. On the other

hand, more than 300 different von Hippel-Lindau muta-

S. M. Yan et al. / J. Biomedical Science and Engineering 2 (2009) 190-199 191

tions have been described at DNA level [21,22,23,24],

and more than 100 at protein level. It would be great

helpful if we can build a quantitative relationship be-

tween von Hippel-Lindau protein mutation and von

Hippel-Lindau disease status, that is, the relationship

between mutant protein and its clinical outcome.

In this study, we build a descriptively quantitative rela-

tionship between changed primary structure of mutated

von Hippel-Lindau protein and the classification of its

clinical outcome, distinguish the classifications of clinical

outcomes as well as the endocrine and nonendocrine neo-

plasia induced by mutations of von Hippel-Lindau protein.

2. MATERIALS AND METHODS

2.1. Data

The human von Hippel-Lindau disease tumor suppr essor

with total 132 mutations (accession number P40337;

December 4, 2007; Entry version 91) is obtained from

UniProtKB/Swiss-Prot entry [25]. Among them, 123 are

missense point mutations , 7 deletions and 3 insertions.

2.2. Amino-Acid Distribution Probability

Among three approaches developed by us, the amino-acid

distribution probability is mainly related to the positions of

amino acids along the protein, which is suitable for mutation

analysis, and we have used this approach in a number of our

previous studies [2,3,4,26,27,28,29,30,31,32,33,34,35,36,37,

38,39,40,41,42,43,44]. The quantification is developed along

such a thought, for example, how do two amino acids dis-

tribute along a protein sequence? Our intuition may suggest

that there would be one amino acid in the first half of the

sequence and anothe r one in the second half. In fact, there are

only three possible distributions, 1) both amino acids are in

the first half, 2) one amino acid is in each half and 3) both

amino acids are in the second half. Thus, each distribution

has the probability of 1 /3. If we do not distinguish either the

first half or second half but are simply interested in whether

both amino acids are in both halves or in any half, there will

be the probability of 1/2 for each distribution.

If we are interested in the distribution probability of

three amino acids in a protein, we naturally imagine to

grouping the protein into three partitions, and our intuition

may suggest that each partition contains an amino acid. If

we do not distinguish the first, second and third partition,

actually there are to tally three types of dis tributions , i.e. 1)

each amino acid is in each partition, 2) two amino acids are

in a partition and an amino acid is in another partition, and

3) three amino aci ds are in a partition.

In this situation, the distribution probability can be

calculated according to the statistical mechanics, which

classifies the distribution of elementary particles in en-

ergy states according to three assumptions of whether

distinguishing each particle and energy state, i.e. Max-

well-Boltzmann, Fermi-Dirac and Bose-Einstein as-

sumptions [45]. We actually use the Maxwell-Boltzmann

assumption for computing amino-acid distribution

probability, which is equal to 

 !...!!

10 n

qqq

rrr

r



 !...!!

[45], where r is the number of amino

acids, n is the number of partitions, rn is the number of

amino acids in the n-th partition, qn is the number of

partitions with the same number of amino acids, and ! is

the factorial function.

Thus, the distribution probabilities are different for

these three types of distributions of three amino acids,

say, 0.2222 for 1), 0.6667 for 2) and 0.1111 for 3).

Clearly the protein can only adopt one type of distribu-

tion for these three amino acids, which is the actual dis-

tribution probability.

For four amino acids, there are five distributions, 1) each

partition contains an amino acid, 2) a partition contains

two amino acids and two partitions contain an amino acid

each, 3) two partitions contain two amino acids each, 4) a

partition contains an amino acid and a partition contains

three amino acids, and 5) a partition contains four amino

acids. Their distribution probabilities are 0.0938 for 1),

0.5625 for 2), 0.1406 for 3), 0.1875 for 4), and 0.0156 for

5). Furthermore, there are seven distributions for five

amino acids, 11 distributions for six amino acids, 15 dis-

tributions for seven amino acids, and so on.

2.3. Quantification of Wild-Type von Hippel-

Lindau Protein

Table 1. Amino acids, their composition and distribution prob-

ability in wild-type human von Hippel-Lindau protein. (A,

alanine; R, arginine; N, asparagine; D, aspartic acid; C, cys-

teine; E, glutamic acid; Q, glutamine; G, glycine; H, histidine; I,

isoleucine; L, leucine; K, lysine; M, methionine; F, phenyla-

lanine; P, proline; S, serine; T, threonine; W, tryptophan; Y,

tyrosine; V, valine.)

Amino acid Number Distribution probability

A 10 0.0476

R 20 0.0067

N 9 0.1770

D 11 0.1077

C 2 0.5000

E 30 0.0001

Q 8 0.0673

G 18 0.0389

H 5 0.0640

I 6 0.1543

L 20 0.0422

K 3 0.1111

M 3 0.6667

F 5 0.2880

P 19 0.0319

S 11 0.0404

T 7 0.2142

W 3 0.6667

Y 6 0.2315

V 17 0.1280

192 S. M. Yan et al. / J. Biomedical Science and Engineering 2 (2009) 190-199

With respect to the wild-type von Hippel-Lindau protein,

for example, there are eight glutamines “Q” in von Hip-

pel-Lindau protein (Table 1). We may ask how these

eight Qs distribute along the von Hippel-Lindau protein?

According to the problem of the occupancy of subpopu-

lations and partition s [45], the simple way to answer this

question is to imagine that we would divide the von Hip-

pel-Lindau protein into eight equal partitions, and each

partition has about 27 amino acids (213/8=26.625) be-

cause the von Hippel-Lindau protein is composed of 213

amino acids, then there would be 22 configurations for all

the possible distributions of eight Qs (Table 2).

Here, we calculate two distribution probabilities in Ta-

ble 2 as example according to the above equation. For

eight Qs equally distribute in each partition (the second

row in Table 2), we have q0=0, q1=8, . . . q8=0; and r1=1,

r2=1, . . . r8=1. Thus, we have the distribution probability,

0.0024

16777216

11111111

40320

1111111403201

40320

!1!1!1!1!1!1!1!1

!0!0!0!0!0!0!0!8!0

!8 8





















Clearly, the von Hippel-Lindau protein can adopt only

one distribution pattern, which is that two partitions

contain zero Q, five partitions contain one Q and one

partition contains three Qs (the fourth row in Tab le 2 ).

So we have q0=2, q1=5, q2=0, q3=1, q4=0, q5=0, q6=0,

q7=0, q8=0; and r1=0, r2=0, r3=1, r4=1, r5=1, r6=1, r7=1,

r8=3, that is,

0.0673

16777216

61111111

40320

11111111202

40320

!3!1!1!1!1!1!0!0

!0!0!0!0!0!0!1!0!5!2

!8 8





















In such a manner, we can quantify each amino acid in

wild-type von Hippel-Lindau protein. Thereafter, we can

assign these probabilities to each amino acid in the von

Hippel-Lindau protein as shown in Figure 1, from which

we get the visual sense of how these distribution prob-

abilities go along the von Hippel-Lindau protein, and

more importantly we can sum up these distribution prob-

abilities together for al l 213 amino acids in t he pr ot ei n.

us a way to estimate the position of am ino acid in a protein,

because there is a standard method for the computation

using Maxwell-Bolzmann assumption, which saves us

from inventing new computational methods. Moreover, the

primary structure is the base for higher - le vel structure, t hus

any mutation in primary structure would lead to the change

in distribution probability, in higher-level structure, and

finally the biological function. This is the biological mean-

ing of use of Maxwell- Bolzmann assumption for quantify-

Actually, the Maxwell-Bolzmann assumption provides

Table 2. All possible distributions of eight glutamines in von Hippel-Lindau protein. (Bold and italic is the real distribution.)

Partition 1 Partition 2 Partition 3 Partition 4 Partition 5 Partition 6 Partition 7 Partition 8 Probability

1 1 1 1 1 1 1 1 0.002403

1 1 1 1 1 1 2 0.0673

1 1 1 1 1 3 0.0673

1 1 1 1 4 0.0280

1 1 1 5 5.6076e-3

1 1 6 5.6076e-4

1 7 2.6703e-5

8 4.7684e-7

1 1 1 1 2 2 0.2523

1 1 1 2 3 0.2243

1 1 2 4 0.0421

1 2 5 3.3646e-3

2 6 9.3460e-5

1 1 2 2 2 0.1682

1 2 2 3 0.0841

2 2 4

4.2057e-3

2 2 2 2 0.0105

1 1 3 3 0.0280

2 3 3 5.6076e-3

1 3 4 5.6076e-3

4 4 1.1683e-4

3 5 1.8692e-4

JBiSE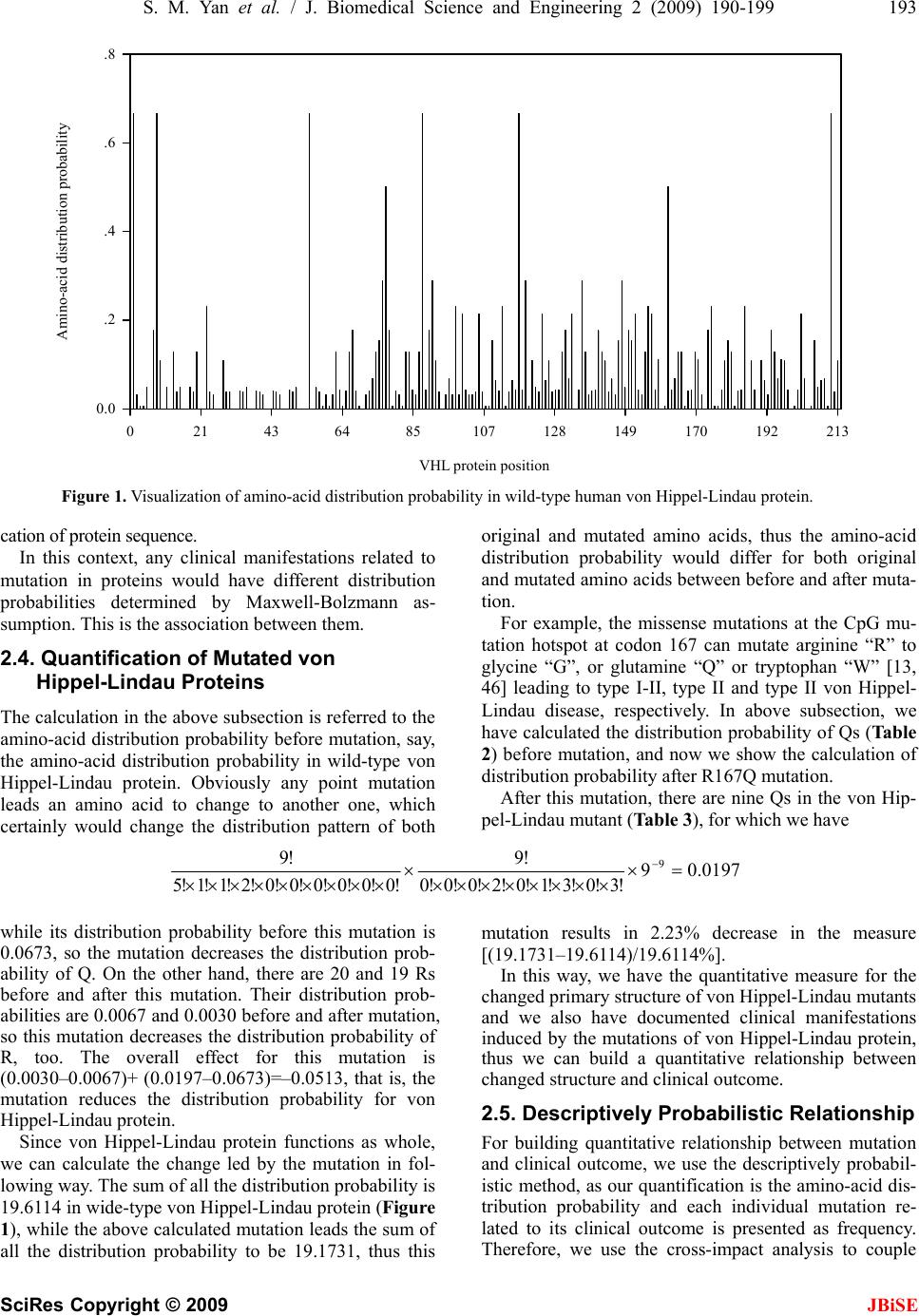

S. M. Yan et al. / J. Biomedical Science and Engineering 2 (2009) 190-199 193

VHL protein position

021436485107 128 149 170 192 213

Amino-acid distribution probability

0.0

VHL protein position

Amino-acid distribution probability

Figure 1. Visualization of amino-acid distribution probability in wild-type human von Hippel-Lindau protein.

cation of protein sequence.

In this context, any clinical manifestations related to

mutation in proteins would have different distribution

probabilities determined by Maxwell-Bolzmann as-

sumption. This is the association between them.

2.4. Quantification of Mutated von

Hippel-Lindau Proteins

The calculation in the abov e subsection is referred to the

amino-acid distribution probability before mutation, say,

the amino-acid distribution probability in wild-type von

Hippel-Lindau protein. Obviously any point mutation

leads an amino acid to change to another one, which

certainly would change the distribution pattern of both

original and mutated amino acids, thus the amino-acid

distribution probability would differ for both original

and mutated amino acids between before and after muta-

tion.

For example, the missense mutations at the CpG mu-

tation hotspot at codon 167 can mutate arginine “R” to

glycine “G”, or glutamine “Q” or tryptophan “W” [13,

46] leading to type I-II, type II and type II von Hippel-

Lindau disease, respectively. In above subsection, we

have calculated the distribution probab ility of Qs (Table

2) before mutation, and now we show the calculation of

distribution probability after R167Q mutation.

After this mutation, there are nine Qs in the von Hip-

pel-Lindau mutant (Table 3), for which we hav e

0.01979

!3!0!3!1!0!2!0!0!0

!0!0!0!0!0!0!2!1!1!5

!9 9









while its distribution probability before this mutation is

0.0673, so the mutation decreases the distribution prob-

ability of Q. On the other hand, there are 20 and 19 Rs

before and after this mutation. Their distribution prob-

abilities are 0.0067 and 0.0030 b efore an d after mutation,

so this mutation decreases the distribution probability of

R, too. The overall effect for this mutation is

(0.0030–0.0067)+ (0.0197–0.0673)=–0.0513, that is, the

mutation reduces the distribution probability for von

Hippel-Lindau protein.

Since von Hippel-Lindau protein functions as whole,

we can calculate the change led by the mutation in fol-

lowing way. The su m of all th e d istribution probab ility is

19.6114 in wide-type von Hippel-Lindau protein (Figure

1), while the above calculated mutation leads the sum of

mutation results in 2.23% decrease in the measure

[(19.1731–19.6114)/19.6114%].

In this way, we have the quan

all the distribution probability to be 19.1731, thus this

titative measure for the

elationship

anged primary structure o f von Hippel-Li ndau mutant s

and we also have documented clinical manifestations

induced by the mutations of von Hippel-Lindau protein,

thus we can build a quantitative relationship between

changed structure and clinical outcome.

2.5. Descriptively Probabilistic R

For building quantitative relationship between mutation

and clinical outcome, we use the descriptively probabil-

istic method, as our quantification is the amino-acid dis-

tribution probability and each individual mutation re-

lated to its clinical outcome is presented as frequency.

Therefore, we use the cross-impact analysis to couple

194 S. M. Yan et al. / J. Biomedical Science and Engineering 2 (2009) 190-199

Partition I II III IV V VI VII VIIIIX

Table 3. Distribution pattern of glutamines before and after

mutation at position 167 in von Hippel-Lindau protein.

Befor e mutation0 0 1 11 1 1 3 -

After mutation 0 0 0 20 1 3 0 3

em [35,47,48,49,50,51,52,53], because the amino-acid

tical

n is based on permutation, and can

nted as mean±SD for normal distribu-

CUSSION

obability in

s on the re-

distribution probability either increases or decreases af-

ter mutation, which is a 2-possibilty event, and the

clinical outcome either occurs or does not occur after

mutation, which is a yes-and-no event. Thereafter, we

can use the Bayesian equation to calculate the probabil-

ity of occurrence of clinical outcome under a mutation.

2.6. Classification of Clinical Outcomes

It is extremely challenging how to use a mathema

modeling to distinguish the clinical outcomes with re-

spect to mutant von Hippel-Lindau protein because of

the variety of clinical outcomes. In an effort towards

solving this problem, we employ our second quantifica-

tion, amino-acid pair pred ictability, whose relational an d

applications have been published intensively (for re-

views, see [2,3,4]).

This quantificatio

calculated in the following way. For example, there

are 30 glutamic acids “E” and 20 Rs in von Hippel-

Lindau protein, the predicted frequency of amino-acid

pair ER would be 3 (30/21320/212212=2.817), while

we do find three ERs in the protein, so the amino- acid

pair ER is predictable. Still, the predicted frequency of

EE would be 4 (30/21329/212212=4.085), but actually

the EE appears nine times in reality. This is the case that

the actual frequenc y is larger than its predicte d one. In this

manner, we can quantify a protein sequence according to

the percentage of how many amino-acid pairs are predict-

able among all the amino-acid pairs in given protein as

well as its mutants. For instance, the predictable portion of

amino-acid pairs is 27.54% in wild-type von Hip-

pel-Lindau protein and 31.88% in its P25L mutant.

2.7. Statistics

The data are prese

tion or median with interquatile range for non-normal

distribution. The Kruskal-Wallis one-way ANOVA and

Chi-square are used for statistical inference, and P < 0.05

is considered significant.

3. RESULTS AND DIS

After computing amino-acid distribution pr

wild-type von Hippel-Lindau protein and in its 132 mu-

tants, we have 132 changed amino-acid distribution

probabilities. Firstly, we can use the cross-impact analy-

sis to build a quantitative relationship between the in-

crease/decrease of distribution probability after muta-

tions and the clinical diag nosis, because the cross-impact

analysis is particularly suited for two relevant events

coupled together [35 ,47,48,49,50,51,52,53].

Figure 2 displays the cross-impact analysi

tionship between changed primary structure and von

Hippel-Lindau disease. At the level of amino-acid dis-

tribution probability, P(2) and



Pare the decreased

and increased probabilities ind ucy mutations, and 53

and 79 mutations result in the distribution probability

decreased and increased, respectively. At the level of

clinical diagnosis: 1)

ed b





2|1P is the impact probability

(conditional probabilitt the von Hippel-Lindau

disease is diagnosed under the condition of increased

distribution probability, and 70 mutations have such an

effect. 2)

y) tha





2|1P is the impact probability that other

disease is sed under the condition of increased

distribution probability, and 9 mutations work in such a

manner. 3) P(1|2) is the impact probability that the von

Hippel-Lindau disease is diagnosed under the condition

of decreased distribution probability, and 44 mutations

play such a role. 4)

diagno





2|1P is the impact probability

that other disease is ded under the condition of

decreased distribution probability, and 9 mutations fall

into this category. At the level of combined events, we

can see the combined results of changed structure and

von Hippel-Lindau disease.

Ta bl e 4 lists the calculate

iagnos

d probabilities with respect

to Figure 2, from which several interesting points can be

drawn. 1) As





2P is larger than P(2), a mutation has a

larger chance of ireasing the distribution probability in

von Hippel-Lindau mutant. 2) As



P much lar-

ger than

2|1 is





2|1P, a mutation that ins the distribu-

tion probabas about n ine ten th chan ce o f b eing vo n

Hippel-Lindau disease. 3) As P(1|2) is much larger than

crease

ility h





2|1P, a mutation that decreases the distribution

lity has much larger chance of being von Hippel-

Lindau disease.

probabi

able 4. Computed probabilities in reference to the cross-im-T

pact analysis in Figure 2.

P(2)=53/132=0.4015





2P=1–P(2)=1–0.4015=0.5985=79/132





2=70/79=0.8861 |1P





2|1P=1–





2|1P=1–0.8861=0.1139=9/79

P(1|2)==0.83044/532





2|1P=1–P(1|2)=1–0.8302=0.1698=9/53





21P=





2|1P×





2P=70/79×79/132=0.5303=70/132





21P=





2|1P×





P(12)= |2)×P=44

=9/79×79/132=0.0682=9/132

P(1 (2)/53×53/132=0.3333=44/132





21P=





2|1P×P(2)=9/53×53/132=0.0682=9/132

S. M. Yan et al. / J. Biomedical Science and Engineering 2 (2009) 190-199 195

Mutation

Probability increases (n = 79)

Probability decreases (n = 53)

P(2)

P(2) = 1 -- P(2)

Di s t ribut ion probabil it y (eve nt 2)Clinical diagnosis (event 1)Combined event

Other d i sea se ( n = 9 )

VHL disease (n = 44)

VHL disease (n = 70)

Other diseas

P(12) = 70/132

JBiSE

e (n = 9)

P(12) = 9/132

P(1|2)

P(1|2) = 1 -- P(1|2)

P(1|2) = 1 -- P(1|

P(12) = 44/132

P(12) = 9/132

Figure 2. Cross-impact relationship among von Hippel-Lindau protein mutation, changed

amino- acid distribution probability, and clinical diagnosis.

Secondly, wse the Bayes’ law

e u







2|1P



1|2 P

P, whindicates the probabilities o

nces of two ev [54], to determine the p

(1), von Hippelndau disease under a mu

ause P(2) and



have already been

ross- imwhile is the p

at the distributrobability con-

ition that the voippel-Lindau disease is diagnosed.

As P(1|2)=44/0.8302 (Table 4), and = 44/

4+70)=0.3860,

ich

ents

-Li



ion p

n H

53=

f occur-

robability,

tation, be-

defined in

robability

c2|

pact analysis,



1|2P

th decreases under the



1|2P

 



3860.0

.08302 4015.0

1|2

2|1



(4 P

0.8635, namely, the patient has nine tenth chance of

eing von Hippel-Lindau disease when a new mutation

found in von Hippel-Lindau protein.

Among patients with von Hippel-Lindau disease,

bout 40% of mutations are genomic deletions and the

st are predominantly truncating or missense mutations,

hich do not occur within the first 53 amino acids

5,56]. In this study, we focus on the mutations of von

ippel-Lindau protein. From a probabilistic viewpo

ur results indicate the chance of being diagnos

von Hippel-Lindau disease when a new von Hippel-

Lindau mutant occurs.

The von Hippel-Lindau disease is characterized by

marked phenotypic variability [5 7,58], due to mosaicism

[59], modifier effects [60], and mainly allelic heteroge-

neity [61]. All these result in complicated clinical classi-

fications. Thus, we use the predictable portion of amino-

acid pairs to model the classifications.

Figure 3 illustrates the classification with respect to

the predictable portion of amino-acid pairs. Although

there are large overlaps among classifications, our quan-

tification already disting uishes them to some degr ee. For

example, in comparison with von Hippel - Lindau disease,

our quantification shows relatively lower in pheochro-

mocytoma and higher in other disorders (P=0.079,

Kruskal-Wallis one-w ay ANOVA). The lack of statistical

significance is certainly, in part, due to few cases in

some groups, however the trend is clear, which paves the

way for further classification using more sophisticated

mathematical models.

Genotype-phenotype relationships have revealed that

a certain number of missense mutations are associated

with a high risk of pheochromocyto ma but the mutatio ns

eir functions are associated with a low

ts with type II von Hippel-Lindau dis-

ease have missense mutations whereas the large dele-

[5int,

ed as the that totally loss th

risk. Most patien

196 S. M. Yan et al. / J. Biomedical Science and Engineering 2 (2009) 190-199

pairs induced by mutations of von Hip-

eo), von Hippel-Lindau disease and other

with an interquatile range (P = 0.079,

Figure 3. Predictable portion of amino-a

pel-Lindau protein in pheochromocytoma

disorders. The data are presented as med

Kruskal-Wallis one-way ANOVA).

cid

(Ph

ian

nendo-

161116 21 27 32 3742 47 52

Figure 4. Distribution of changed amino-acid d

crine neoplasia induced by mutations of von

istribution probability in endocrine and no

Hippel-Lindau protein (P = 0.094, Chi-square).

Changed amino-acid distribution probability (%)

-10

Endocrine neoplasia

Mutants in von Hippel-Linda u protein

1713 19 25 32 38 44 50 56 62

Changed amino-acid distribution probability(%)

Nonendocrine neoplasia

Nonendocrine neopla sia

-20

-10

Mutants in von Hippel-Lindau protein

S. M. Yan et al. / J. Biomedical Science and Engineering 2 (2009) 190-199 197

ype I

ribution probability (upper panel),

h might provide the much clearer pattern,

l viewpoint, one could consider t

is different. Without suc

t a theoretical study finds

ical assays. Our ap-

tions and truncating mutations predominate in t

families [11,19,62,63]. Many missense mutations caus-

ing a type I phenotype are involved in the core hydro-

phobic residues and were predicted to disrupt protein

structure, whereas type II phenotype missense mutations

nvolved in substitutiare ions at a surface amino acid that

does not cause a total loss of function [64,65].

Figure 4 displays the distribution of changed amino-

acid distribution probability in endocrine neoplasia

(pheochromocytoma, type II von Hippel-Lindau disease)

and nonendocrine neoplasia (type I von Hippel-Lindau

disease). As can be seen, the mutations that led to the

endocrine neoplasia have the trend to increase the

amino-acid dist

whereas the mutations that led to nonendocrine neopla-

sia have the effect to either increase or decrease the

amino-acid distribution probability (lower panel). The

difference between two panels is mainly considered

from view of symmetry. As the x-axis is related to the

number of von Hippel-Lindau mutations, this figure

would be different when more mutations would be found

in future, whic

although we did not find the statistical difference be-

tween two panels (P=0.094, Chi-square) now.

From a theoreticao No.

calculate the distribution probability of all 19 potential

types of mutations at each position of von Hippel-Lindau

protein, and then find the link between mutations and

clinical outcomes. However, the amount of computation

is huge because it would be equal to 2.36910272 muta-

tions (19213), which is not only beyond the capacity of

any computers, but also beyond the capacity for com-

parison. Actually, we really know that each position does

not have 19 types of potential mutations, because this

mutation process is gov erned by the tran slation probab il-

ity between RNA codon and mutated amino acids [66,

67,68]. On the other hand, our study is focused on the

documented data rather than the simulated data.

In this study, we use a single valu e, the sum of all dis-

tribution probability to represent the normal von Hippel-

Lindau protein and its mutated proteins, respectively,

because there is no other way to use a single value dy-

namically to represent a protein, namely, the value is

different when a proteinh a

measure, we cannot model a protein dynamically with its

mutations. To the best of knowledge, currently it is only

the accession number that can represent a protein

uniquely, however it has nothing to do with the protein

itself, i.e. composition, length, function, etc.

In general, one would hope to verify this type of study

against the real-life cases, which is possible in future

although it would deal with a large-scale collaboration

because this type of diseases is not frequently seen in

clinical settings, for example, the von Hippel-Lindau

disease has a birth incid ence of abou t 1 in 36 000 [11,12].

It will take years to verify wha

with fast-speed computational technique. Even, we can-

not verify all the theoretical studies, for example, we

cannot create another earth without global warming.

The implications of this study include two aspects. 1)

relationship between changed primary structTheure and

changed function is very meaningful, because it provides

the dynamic rather than static relationship between mu-

tant protein and its function. This can furthermore pro-

vide us the basis for building a dynamic model to predict

the new function in mutant proteins. Nevertheless, we

need to quantify the proteins in order to build a dynamic

model and this study is doing in su ch a way. 2) Fro m the

clinical viewpoint, the classification of von Hippel-

Lindau disease as well as many mutation related diseases

needs a considerable amount of clin

proach can provide a probabilistic estimate for disease

classification after determining which amino acid has

mutated, because the primary structure of protein is the

base for its high-level structure and function.

4. ACKNOWLEDGEMENTS

This study was partly supported by Guangxi Science Foundation (No.

0537012-G and 0991080), and Guangxi Academy of Sciences (project

9YJ17SW07).

REFERENCES

[1] K. C. Chou, (2004) Structure bioinformatics and its im-

pact to biomedical science, Curr. Med. Chem, 11,

2105-2134.

[2] G. Wu and S. Yan, (2002) Randomness in the primary

structure of protein: Methods and implications, Mol. Biol.

Today, 3, 55-69.

[3] G. Wu and S. Yan, (2006) Mutation trend of hemaggluti-

nin of influenza A virus: A review from computational

mutation viewpoint, Acta Pharmacol. Sin., 27, 513-526.

[4] G. Wu and S. Yan, (2008) Lecture notes on computational

mutation, Nova Science Publishers, New York, 2008.

[5] Von Hippel, (1911) Die anatomische Grund lage der von

mir beschriebenen ‘sehr seltenen Erkrankung der Netz-

haut’, Graefes. Arch. Ophthalmol., 79, 350-377.

[6] A. Lindau, (1926) Studien uber kleinhirncysten, bau,

pathogenese und bezoejimgem zur angiomatosis retinae,

Acta Pathol. Microbiol. Scand., Suppl 1, 1-128.

[7] K. L. Melmon and S. W. Rosen, (1964) Lindau’s disease,

Am. J. Med., 36, 595-617.

[8] V. V. Michels, (1988) Investigative studies in von Hip-

pel-Lindau disease, Neurofibromatosis, 1, 159-163.

[9] H. P. Neumann, (1987) Basic criteria for clinical diagno-

sis and genetic counselling in von Hippel-Lindau syn-

drome, Vasa, 16, 220-226.

[10] R. R. Lonser, G. M. Glenn, M. Walther, E. Y. Chew, S. K.

Libutti, W. M. Linehan, and E. H. Oldfield, (2003) von

Hippel-Lindau disease, Lancet, 361, 2059-2067.

[11] E. R. Maher, A. R. Webster, F. M. Richards, J. S. Green,

P. A. Crossey, S. J. Payne, and A. T. Moore, (1996) Phe-

notypic expression in von Hippel-Lindau disease: Corre-

198 S. M. Yan et al. / J. Biomedical Science and Engineering 2 (2009) 190-199

Mol. Genet., 4,

ity by the von

Kaelin, (2002) Molecular basis of the VHL

er, and oxygen sensing, J. Am. Soc. Nephrol.,

gical basis, clinical criteria, genetic testing,

. Tory, I. Kuzmin, T. Stackhouse, F. Latif, W.

lations with phenotype, Hum. Mutat.,

mas, (1998) Germ-

von Hip-

von Hippel-Lindau disease tumor

suppressor gene, Hum. Mutat., 12, 417-423.

5] A. Bairoch and R. Apweiler, (2000) The SWISS-PROT

protein sequence data bank and its supplement TrEMBL

cid pairs in human haemoglobin

alysis of presence

Analysis of distributions of

-198.

lations with germline VHL gene mutations, J. Med.

Genet., 33, 328-332.

[12] F. M. Richards, S. J. Payne, B. Zbar, N. A. Affara, M. A.

Ferguson-Smith, and E. R. Maher, (1995) Molecular

analysis of de novo germline mutations in the von Hip-

pel-Lindau disease gene, Hum.

2139-2143.

[13] F. Latif, K. Tory, J. Gnarra, M. Yao, F. M. Duh, M. L.

Orcutt, et al., (1993) Identification of the von Hip-

pel-Lindau disease tumor suppressor gene, Science, 260,

1317-1320

[14] P. O. Schnell, M. L. Ignacak, A. L. Bauer, J. B. Striet, W.

R. Paulding, and M. F. Czyzyk-Krzeska, (2003) Regula-

tion of tyrosine hydroxylase promoter activ [28]

Hippel-Lindau tumor suppressor protein and hy-

poxia-inducible transcription factors, J. Neurochem., 85,

483-491.

[15] W. G. Jr.

hereditary cancer syndrome, Nat. Rev. Cancer, 2,

673-682.

[16] W. G. Jr. Kaelin, (2003) The von Hippel-Lindau gene,

kidney canc

14, 2703 -2711.

[17] T. Shuin, I. Yamasaki, K. Tamura, H. Okuda, M. Furihata,

and S. Ashida, (2006) Von Hippel-Lindau disease: Mo-

lecular patholo

and a

clinical features of tumors and treatment, Jpn. J. Clin.

Oncol., 36, 337-343.

[18] M. Ohh, (2006) Ubiquitin pathway in VHL cancer syn-

drome, Neoplasia, 8, 623-629.

[19] F. Chen, T. Kishida, M. Yao, T. Hustad, D. Glavac, M.

Dean, J. R. Gnarra, M. L. Orcutt, F. M. Duh, G. Glenn, J.

Green, Y. E. Hsia, J. Lamiell, H. Li, M. H. Wei, L.

Schmidt, K

M. Linehan, M. Lerman, and B. Zbar, (1995) Germline

mutations in the von Hippel-Lindau disease tumor sup-

pressor gene: Corre

5, 66-75.

[20] S. Lee, E. Nakamura, H. Yang, W. Wei, M. S. Linggi, M.

P. Sajan, R. V. Farese, R. S. Freeman, B. D. Carter, W. G.

Jr. Kaelin, and S. Schlisio, (2005) Neuronal apoptosis

linked to EglN3 prolyl hydroxylase and familial phaeo-

chromocytoma genes: developmental culling and cancer.

Cancer Cell, 8, 1-13.

[21] Clinical Research Group for VHL in Japan, (1995)

Germline mutations in the von Hippel-Lindau disease

(VHL) gene in Japanese VHL, Hum. Mol. Genet., 4,

2233-2237.

[22] H. P. Neumann, B. Bender, I. Zauner, D. P. Berger, C.

Eng, H. Brauch, and B. Zbar, (1996) Monogenetic hy-

pertension and pheochromocytoma, Am. J. Kidney Dis.,

28, 329-333.

[23] S. Olschwang, S. Richard, C. Boisson, S. Giraud, P.

Laurent- Puig, F. Resche, and G. Tho

line mutation profile of the VHL gene in

pel-Lindau disease and in sporadic hemangioblastoma,

Hum. Mutat., 12, 424-430.

[24] C. Stolle, G. Glenn, B. Zbar, J. S. Humphrey, P. Choyke,

M. Walther, S. Pack, K. Hurley, C. Andrey, R. Klausner,

and W. M. Linehan, (1998) Improved detection of germ-

line mutations in the

in 2000, Nucleic Acids Res., 28, 45-48.

[26] N. Gao, S. Yan, and G. Wu, (2006) Pattern of positions

sensitive to mutations in human haemoglobin -chain,

Protein Pept. Lett., 13, 101-107.

[27] G. Wu and S. Yan, (2000) Prediction of distributions of

amino acids and amino a

-chain and its seven variants causing-thalassemia from

their occurrences according to the random mechanism,

Comp. Haematol. Int, 10, 80-84.

G. Wu and S. Yan, (2001) Analysis of distributions of

amino acids, amino acid pairs and triplets in human

insulin precursor and four variants from their occur-

rences according to the random mechanism, J. Bio-

chem. Mol. Biol. Biophys., 5, 293-300.

[29] G. Wu and S. Yan, (2001) Analysis of distributions of

amino acids and amino acid pairs in human tumor necro-

sis factor precursor and its eight variants according to

random mechanism, J. Mol. Model, 7, 318-323.

[30] G. Wu and S. Yan, (2002) Random an

bsence of two-and three-amino-acid sequences and

distributions of amino acids, two- and three-amino-acid

sequences in bovine p53 protein, Mol. Biol. Today, 3,

31-37.

[31] G. Wu and S. Yan, (2002)

amino acids in the primary structure of apoptosis regula-

tor Bcl-2 family according to the random mechanism, J.

Biochem. Mol. Biol. Biophys, 6, 407-414.

[32] G. Wu and S. Yan, (2002) Analysis of distributions of

amino acids in the primary structure of tumor suppressor

p53 family according to the random mechanism, J. Mol.

Model, 8, 191

[33] G. Wu and S. Yan, (2004) Determination of sensitive

positions to mutations in human p53 protein, Biochem.

Biophys. Res. Commun., 321, 313-319.

[34] G. Wu and S. Yan, (2005) Searching of main cause lead-

ing to severe influenza A virus mutations and conse-

quently to influenza pandemics/epidemics, Am. J. Infect.

Dis., 1, 116-123.

[35] G. Wu and S. Yan, (2005) Prediction of mutation trend in

hemagglutinins and neuraminidases from influenza A vi-

ruses by means of cross-impact analysis, Biochem. Bio-

phys. Res. Commun., 326, 475-482.

G. Wu and S. Yan, (2006) Timing

[36] of mutation in hemag-

glutinins from influenza A virus by means of amino-acid

distribution rank and fast Fourier transform, Protein Pept.

Lett., 13, 143-148.

[37] G. Wu and S. Yan, (2006) Prediction of possible muta-

tions in H5N1 hemagglutinins of influenza A virus by

means of logistic regression, Comp. Clin. Pathol., 15,

255-261.

[38] G. Wu and S. Yan, (2006) Prediction of mutations in

H5N1 hemagglutinins from influenza A virus, Protein

Pept. Lett., 13, 971-976.

[39] G. Wu and S. Yan, (2007) Improvement of model for

prediction of hemagglutinin mutations in H5N1 influenza

S. M. Yan et al. / J. Biomedical Science and Engineering 2 (2009) 190-199 199

guishing of arginine, leucine and ser-

ine, Protein Pept. Lett., 14, 191-196.

0] G. Wu and S. Yan, (2007) Improvement of prediction of

mutation positions in H5N1 hemagglutinins of influenza

A virus using neural network with distinguishing of ar-

ginine, leucine and serine, Protein Pept. Lett., 14,

465-470.

1] G. Wu and S. Yan, (2007) Prediction of mutations engi-

neered by randomness in H5N1 neuraminidases from in-

fluenza A virus, Amino Acids, 34, 81-90.

2] G. Wu and S. Yan, (2007) Prediction of mutations in H1

neuraminidases from North America influenza A virus

engineered by internal randomness, Mol. Divers., 11,

131-140.

[43] G. Wu and S. Yan, (2008) Prediction of mutations initi-

ated by internal power in H3N2 hemagglutinins of influ-

enza A virus from North America, Int. J. Pept. Res. Ther.,

14, 41-51.

[44] G. Wu and S. Yan, (2008) Prediction of mutation in

H3N2 hemagglutinins of influenza A virus from North

America based on different datasets, Protein Pept. Lett.,

15, 144-152.

[45] W. Feller, (1968) An introduction to probability theory

and its applications, 3rd ed, Wiley, New York, 1, 34-40.

[46] B. Zbar, T. Kishida, F. Chen, L. Schmidt, E. R. Maher, F.

M. Richards, P. A. Crossey, A. R. Webster, N. A. Affara,

M. A. Ferguson-Smith, et al., (1996) Germline mutations

in the Von Hippel-Lindau disease (VHL) gene in families

from North America, Europe, and Japan, Hum. Mutat., 8,

348-357.

[47] T. G. Gordon and H. Hayward, (1968) Initial experiments

with the cross-impact matrix method of forecasting, Fu-

tures, 1, 100-116.

[48] T. G. Gordon, (1969) Cross-impact matrices - an illustra-

tion of their use for policy analysis, Futures, 2, 527-531.

[49] S. Enzer, (1970) Delphi and cross-impact techniques: an

effective combination for systematic futures analysis,

Futures, 3, 48-61.

[50] S. Enzer, (1970) Cross-impact techniques in technology

assessment, Futures, 4, 30-51.

[51] A. P. Sage, (1977) Methodology for large-scale systems,

McGraw-Hill, New York, 165-203.

[52] G. Wu, (2000) Application of cross-impact analysis to the

relationship between aldehyde dehydrogenase 2 and

flushing, Alcohol Alcohol., 35, 55-59.

[53] G. Wu and S. Yan, (2008) Building quantitative relation-

ship between changed sequence and changed oxygen af-

finity in human hemoglobin-chain, Protein Pept. Lett., 15,

341-345.

[54] Wikipedia, (2008) Bayes’ theorem,

http://en.wikipedia.org/wiki/ Bayes’_theorem.

[55] S. O. Ang, H. Chen, K. Hirota, V. R. Gordeuk, J. Jelinek,

Y. Guan, E. Liu, A. I. Sergueeva, G. Y. Miasnikova, D.

Mole, P. H. Maxwell, D. W. Stockton, G. L. Semenza,

and J. T. Prchal., (2002) Disruption of oxygen homeosta-

sis underlies congenital Chuvash polycythemia, Nature

Genet., 32, 614-621.

[56] Y. Pastore, K. Jedlickova, Y. Guan, E. Liu, J. Fahner, H.

Hasle, J. F. Prchal, and J. T. Prchal., (2003) Mutations of

von Hippel- Lindau tumor-suppressor gene and congeni-

tal polycythe mia, Am. J. Hum. Gene t. , 73, 412 -419.

[57] E. R. Maher, (2004) Von Hippel-Lindau disease, Curr.

Mol. Med., 4, 833-842.

[58] E. R. Woodward and E. R. Maher, (2006) Von Hip-

pel-Lindau disease and endocrine tumour susceptibility,

End. Relat. Cancer, 13, 415-425.

[59] M. T. Sgambati, C. Stolle, P. L. Choyke, M. M. Walther,

B. Zbar, W. M. Linehan, and G. M. Glenn, (2000) Mo-

saicism in von Hippel-Lindau disease: lessons from kin-

dreds with germline mutations identified in offspring

with mosaic parents, Am. J. Hum. Genet., 66, 84-91.

[60] A. R. Webster, F. M. Richards, F. E. MacRonald, A. T.

Moore, and E. R. Maher, (1998) An analysis of pheno-

typic variation in the familial cancer syndrome von

Hippel-Lindau disease: evidence for modifier effects,

Am. J. Hum. Genet., 63, 1025-1035.

[61] P. A. Crossey, C. Eng, M. Ginalska-Malinowska, T. W. J.

Lennard, J. R. Sampson, B. A. J. Ponder, and E. R.

Maher, (1995) Molecular genetic diagnosis of von Hip-

pel-Lindau disease in familial phaeochromocytoma, J.

Med. Genet., 32, 885-886.

[62] P. A. Crossey, F. M. Richards, K. Foster, J. S. Green, A.

Prowse, F. Latif, M. I. Lerman, B. Zbar, N. A. Affara, M.

A. Ferguson-Smith, and R. Maher, (1994) Buys CHCM,

identification of intragenic mutations in the von Hip-

pel-Lindau disease tumour suppressor gene and correla-

tion with disease phenotype, Hum. Mol. Genet., 3,

1303-1308.

[63] E. R. Maher, A. R. Webster, F. M. Richards, J. S. Green,

P. A. Crossey, S. J. Payne, and A. T. Moore, (2000) Phe-

notypic expression in von Hippel-Lindau disease: corre-

lations with germline VHL gene mutations, J. Med.

Genet., 37, 62-63.

[64] C. E. Stebbins, W. G. Jr. Kaelin, and N. P. Pavletich,

(1999) Structure of the VHL-ElonginC-ElonginB com-

plex: Implications for VHL tumor suppressor function,

Science, 284, 455-461.

[65] S. J. Marx and W. F. Simonds, (2005) Hereditary hor-

mone excess: Genes, molecular pathways, and syn-

dromes, End. Rev., 26, 615-661.

[66] G. Wu and S. Yan, (2005) Determination of mutation

trend in proteins by means of translation probability be-

tween RNA codes and mutated amino acids, Biochem.

Biophys. Res. Commun., 337, 692-700.

[67] G. Wu and S. Yan, (2006) Determination of mutation

trend in hemagglutinins by means of translation prob-

ability between RNA codons and mutated amino acids,

Protein Pept. Lett., 13, 601-609.

[68] G. Wu and S. Yan, (2007) Translation probability be-

tween RNA codons and translated amino acids, and its

applications to protein mutations, in: Leading-Edge

Messenger RNA Research Communications, ed. Os-

trovskiy M. H. Nova Science Publishers, New York,

Chapter 3, 47-65.

JBiSE

viruses with distin