Journal of Computer and Communications, 2014, 2, 188-195
Published Online March 2014 in SciRes. http://www.scirp.org/journal/jcc
http://dx.doi.org/10.4236/jcc.2014.24025
How to cite this paper: Mao, J. and Shioya, H. (2014) A Refinement of Extracting Approximate Symmetry Planes Based on
Least Square. Journal of Computer and Communications, 2, 188-195. http://dx.doi.org/10.4236/jcc.2014.24025
A Refinement of Extracting Approximate
Symmetry Planes Based on Least Square
Jun Mao1,2, Hiroyuki Shioya2
1College of Computer Science and Technology, Henan Polytechnic University, Jiaozuo, China
2Computer Science and Systems Engineering, Muroran Institute of Technology, Muroran, Japan
Received October 2013
Abstract
Extracting approximate symmetry planes is a challenge due to the difficulty of accurately measur-
ing numerical values. Introducing the approximate symmetry planes of a 3D point set, this paper
presents a new method by gathering normal vectors of potential of the planes, clustering the high
probability ones, and then testing and verifying the planes. An experiment showed that the me-
thod is effective, robust and universal for extracting the complete approximate planes of symme-
try of a random 3D point set.
Keywords
Approximate Symmetry Plane; 3D Point Set; Least Squares
1. Introduction
Detection of symmetry plays an important role in how we recognize and understand the world around us for
many objects are characterized by the presence of such patterns. Humans recognize a shape not only by its local
and global geometrical variations, but also by a high-level understanding of the structure of the shape. Most pre-
vious works concentrated on characterizing the local geometry or topology but ignored an important global
structural shape descriptor: symmetry. Humans have been shown to be very sensitive to symmetry in visual pat-
terns, and symmetry is detected and recognized rapidly [1].
Symmetry also abounds in man-made objects, often as a result of economic, manufacturing, functional, or
aesthetic considerations. One of the most prominent examples is organisms: biological symmetries are found in
almost all species.
Discovering regular features in a 3-D model is a challenging task, since we typically have no prior knowledge
of the size, shape, or location of the individual elements that define the pattern. Structures can be incomplete or
corrupted by noise, and hidden among large components of the 3-D models that are not part of the pattern and
therefore function as clutter or outliers.
The problem of symmetry detection has been extensively studied in numerous fields, including visual percep-
tion, computer vision, robotics, and computational geometry. Many applications of object recognition or identi-
fication involve symmetry features associated with point sets, a widely-encountered problem in the detection of

J. Mao, H. Shioya
189
bilateral symmetry [2], reverse engineering [3], and 3D MR brain image processing [4]. Early methods concen-
trated on finding perfect symmetries in 2D or 3D planar point sets [5,6].
This paper presents a method for extracting approximate planes, which predicts the norm vectors by the
least-squares point-set matching algorithm in order to evaluate the degree of symmetry by measuring the simi-
larity between two point sets, the original one and the projected one. An effective, robust, universal algorithm
for identifying the most approximate symmetry planes from a point set is proposed.
2. Definitions and Problem Statement
2.1. Approxi mate Sym metry P lan es
In general, symmetry is defined as follows: An n-dimensional object has mir ror -symmetry if it is invariant under
reflection about a hyper-plane of dimension (n-1) passing through the center of mass of the object. Thus, a 2D
object is mirror-symmetric if it is invariant under reflection about a line (called the axis of mirror-symmetr y) and
a 3D object is mirror-symmetric if it is invariant upon reflection about a plane.
A 2D object has rotational-symmetry of order n if it is invariant under rotation of
2/ n π
radians about the
centroid of the object. A 3D object has rotational-symmetry of order n if it is invariant under rotation of
2/n π
radians about an axis passing through the centroid of the object. This axis is the rotational symmetry axis. Rota-
tional symmetry of order n is denoted as Cn-Symmetry [7,8].
The general mathematical definition of symmetry is inadequate to describe and quantify the symmetries found
in the natural world or those found in the visual world. Furthermore, even perfectly symmetric objects lose their
exact symmetry when projected onto the image plane or the retina due to occlusion, perspective, transformation
digitization, and so forth. Thus, although symmetry is usually considered to be a binary feature, i.e. an object is
either symmetric or it is not symmetric, we view symmetry as a continuous feature where intermediate values of
symmetry denote some intermediate amount of symmetry. Zabrodsky introduced a “Symmetry Distance” that
can measure and quantify all types of symmetries of objects [9-11]. Focusing on a comparison of the “amount” of
symmetry of different shapes and the amount of different symmetries of a single shape, the definition benefits
less extracting the axis or planes of mirror-symmetry. Instead, a definition of approximate mirror-symmetry
emphasis in describing the relationship between approximate mirror-symmetry and the axis or planes of mirror-
symmetry is given in what follows in the passage.
Unless noted otherwise, the following notations are used in this paper:
• Matrices are denoted by boldface capital letters, such as
,,PWX
.
• Vectors are denoted by boldface lowercase letters, such as
,,pwx
.
• Scalars are denoted by lowercase letters or Greek letters, such as
,,,, ,
pwx αβδ
.
• The norm of a vector
x
is denoted by
x
.
• The transpose of a matrix
X
is denoted by
′
X
or
t
X
.
• The transpose of a vector
x
is denoted by
′
x
or
t
x
.
2.2. Mirror-Symmetry Point Set of Random Plane
In
3

, given a point set
P
{ }
1 123
,,(p,) ,1,,,,
t
niii i
ppin= ==Pp pp
and random plane
π
0 123
:0,( ,,)1
tt
ww wwand π += ==wx ww
for
i
∈pP
, the m irro r-symmetry point
i
′ p
can be obtained by the following equation, as shown in Figure 1:
0
2( )
t
ii i
′= −+ppwpw w
(1)
Then we obtain the mirror-symmetry point set
′P
of
P
about the plane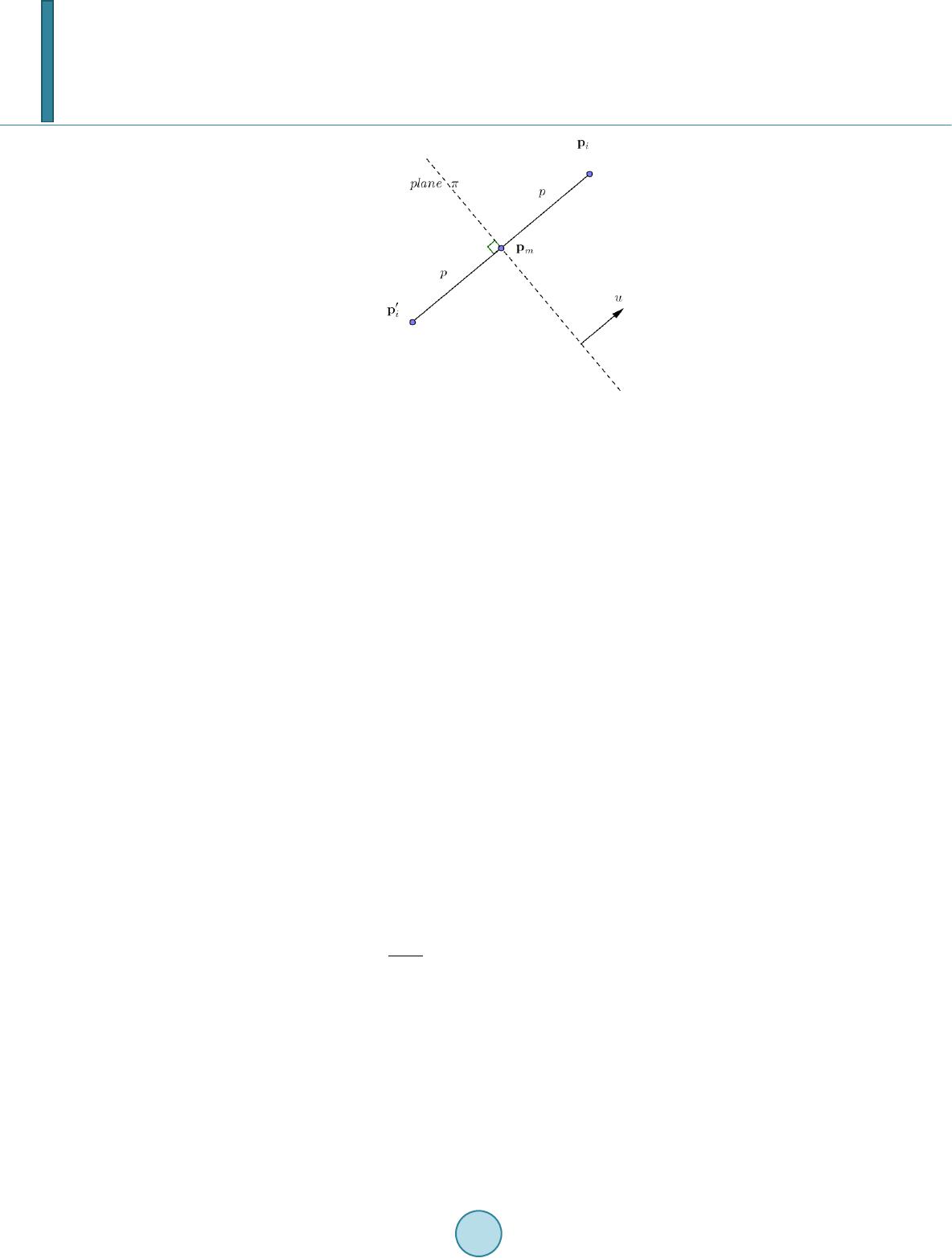
π
:

J. Mao, H. Shioya
190
Figure 1. The mirror-symmetry point pair.
{ }
1 123
,,(p,pp) ,1,,,,
t
niii i
in
′′′′′ ′
=′ ==Pp pp
2.3. Least-Squares Distance between P and P′
Referring to [12,13], the distance between
P
and
′P
,
,()D′PP
, is defined as:
2
11
1
1
( ,)min
1,1, 2,,
1,1,2,,
01,,1, 2,,
.
nn
ij ij
ij
n
ij
i
n
ij
j
ij
Dx
xj n
xi n
xor i
t
jn
s
= =
=
=
′= −′
= =
=



=
= =





∑∑
∑
∑
PPp p



‖‖
(2)
Suppose that
1
ij
x=
, then the point
i
p
and point
j
′p
are called a Least-Squares Point Pair (LSPP), and
i
p
and
j
p
are called Original Least-Squares Point Pair (OLS PP), where
j
∈pP
.
As shown in Figure 2,
1
p
and
1
′p
are a LSPP, and
2
p
and
3
′p
are a LSPP too.
1
p
and itself are an
OLSPP, and
2
p
and
3
p
are an OLSPP.
2.4. Definition of ε-Approximate Mirror-Sym m etry
Referring to the definition of exact mirror-symmetry, the definition of approximate mirror-symmetry is as fol-
lows:
In
3

, given a point set
P
,
1
n
i
i
c
n
=
=
∑
p
p
, if there exists plane
π
:
123
:0,( ,,)1
tt t
c
w wwand π −== =wx wpww 
Satisfied
min( ,)D ε ′=PP
(3)
′
P
is the mirro r-symmetry point set
′
P
of
P
about the plane
π
, and
0 ε ≥
is sufficiently small, for in-
stance,
1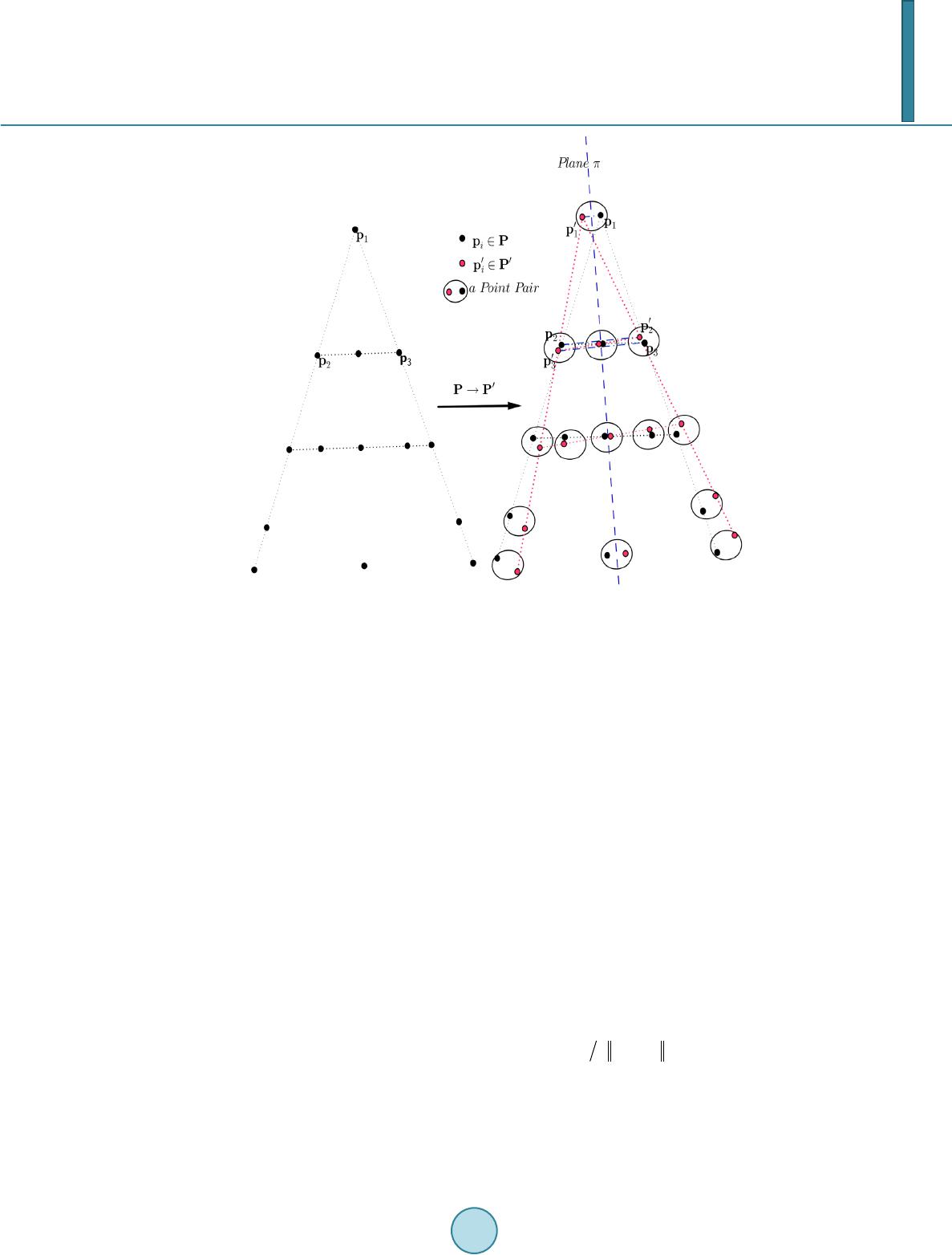
,0
n
ic
i
α αε
=
−≤ →
∑
pp
(4)

J. Mao, H. Shioya
191
Figure 2. Distance between point set P and P′.
Then if
0
ε =
, the point set
P
is mirror-symmetrical about the plane
π
. If
ε
is positive and sufficiently
small, then the point set
P
is approximately mirror-symmetrical about
π
.
3. Probability Distribution Method
Any OLSSP defines a unique reflection with respect to the bisector plane through
/2( )
ij
+pp
with normal di-
rection
ij
−pp
. Hence, such a pair provides evidence for the existence of this specific reflective symmetry.
By looking at all such pairs we can accumulate this evidence and extract the relevant symmetry relation(s).
Only if many point pairs agree on (roughly) the same reflection plane do we have reason to believe that the cor-
responding symmetry is truly present in the set. Thus, we can detect potential symmetries by looking at clusters
of points in the space of transformations as shown in Figure 3 [14].
3.1. Pairing
Suppose that
i
p
and
j
p
are OLSPP. We assume that
1
d
is small enough and
1 23
d min{,}dd  
is sa-
tisfied, where
1ij
d−′=pp 
,
2ic
d= −pp
and
3jc
d= − pp
.
As shown in Figure 4, let
,,
ci j
∈′w ppp
,
( )0
tcm
′−=wp p
,
1=′w
then
cos β ′=ww
,
max
ββ ≤
,
max 1
sin()d 2
cm
β = −pp
where,
()/2, ()/2
mijmj j
+′= ′=+p ppppp
,
and

J. Mao, H. Shioya
192
Figure 3. Clustering unit normal vectors of potential planes of symmetry.
Figure 4. The relation between W and W′.
m } n ,i{
cmic jc
− −≥ −pppp pp 
.
So,
max
sin()0,cos1 ββ →→
, and finally
≈′ww
.
The above features of OLSPP can be used to choose the potential OLSPP and the planes of mirror-symmetry.
3.2. Mean-Shift Clustering
After pairing, no more than
n(n1) / 2−


unit normal vectors
′w
are obtained. If there are enough (nearl y
/2n
) normal vectors in a small district or cluster, then a plane of symmetry is assumed and the district is called
a high-density cluster. Note here that the point set is assumed to be non-collinear. Of course, it is not hard to
check the collinearity of the point set.
We use mean-shift clustering [15] to locate the maximum of the density function. The window radius
r
is

J. Mao, H. Shioya
193
suggested to be
2)(
ic
ε
−
∑pp
. Finding that the window contains more than
3
n
nodes, the averages of each node
set are potential norm vectors of approximate symmetry planes.
Note that if
12 1
t′′
→−ww
, the two vectors in fact correspond to the same plane.
3.3. Extraction
A significant vector detected by the mean-shift clustering algorithm does not necessarily correspond to a mea-
ningful symmetry. Since the spatial relation of sample points is lost during the mapping to transformation space,
sample pairs from uncorrelated parts of the object can accumulate to form discernible clusters. We use Equation
(1), Equation (2) and Equation (3) to check these candidate norm vectors.
Suppose that
′w
is a potential norm vector, then the potential plane of symmetry is
123
: 0,
(, , )
tt
c
t
www
π ′ ′−′=
′=′ ′ ′
wx wp
w
Using Equation (1), the symmetry point set
′P
of
P
corresponding to
π ′
can be determined. By the Iter-
ative Closest Point (ICP ) [16] algorithm employed to minimize the difference between two clouds of points, we
can count out
(, )D′PP
. Using Equation (3), it is decided whether the plane is one of the approximate planes or
not.
4. Experimental Results
The results of applying the proposed method to specially designed data are described. Evaluation data were de-
signed to test the algorithm.
4.1. Illustration of Data
As shown in Fi gu re 5, to make the results of the algorithm more appreciable, a point set
P
(480 points, 480 ×
3 matrix) was evenly picked from the surface of a 3D “heart-lik e” surface, which was mesh-gridded from the
implicit function
22 232323
((9 / 4)1)(9 /80)fxy zxzyz= ++−−−
which evidently embodies only two symmetry planes:
0= x
and
0=y
.
Then, as shown in Figure 6, normally distributed random noise was added to each point.
= +PPN
(5)
N
is a
0, 0.02 µσ = =
, normally distributed random 480 × 3 matrix.
4.2. Experimental Results and Analysis
By our method, as shown in Figure 6, four corresponding mirror symmetry point sets (marked by red +), are
shown, and in Table 1, the numeral values valve can be checked in Table 1. For the wildly errors of NO.(a) and
NO.(d), which are also shown present in the figure, the corresponding vectors are rejected.
For
c
p
= (1.2943e−003, −9.5077e−004, 2.6443e−001)t
So, the outcome planes are
(−1.2389e−003, −9.9809e−001, 2.2970e−003)
x
+ (1.5547e−003) = 0
and
(−9.8665e−001, 7.6978e−003, −2.9780e−002)
x
− (9.1590e−003) = 0.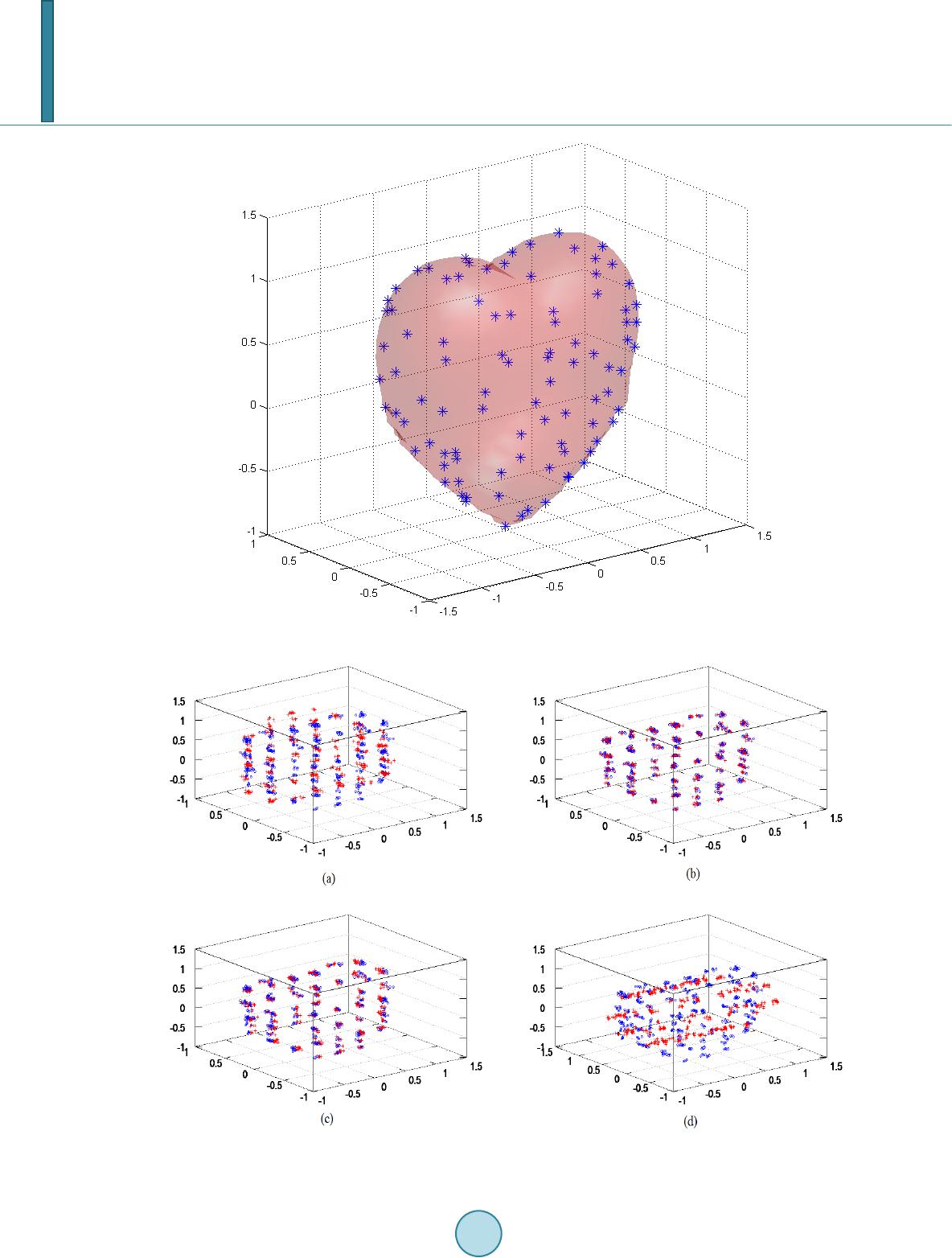

J. Mao, H. Shioya
194
Figure 5. Picking point set P from a 3D “heartlike” surface.
Figure 6. P and P′ corresponding four candidate vectors.

J. Mao, H. Shioya
195
Table 1. Four final candidate vectors.
Figure No. Norm vector, errors and results
Norm vector Error Results
8(a) −4.4745e−003, 1.7389e−002, 9.8743e−001 7.5958e−002 No
8(b) −1.2389e−003, −9.9809e−001, 2.2970e−003, , 2.2518e−002 Yes
8(c) −9.8665e−001, 7.6978e−003, −2.9780e−002, 2.4563e−002 Yes
8(d) 3.3643e−003, −8.6846e−001, −4.8384e−001, 8.8539e−002 No
5. Acknowledgements
I would like to thank Jianming Shi for his encouragement, patience and expert advice, and my family, especially
my wife and my son, and friends of Muroran Institute of Technology and Henan Polytechnic University, who
have supported me throughout my research.
References
[1] Blakemore, C. and Campbell, F. (1969) On the Existence of Neurones in the Human Visual System Selectively Sensi-
tive to the Orientation and Size of Retinal Images. The Journal of Physiology, 203, 237-260.
[2] Dakin, S. C. and Watt, J. (2002) Detection of Bilateral Symmetry Using Spatial Filters. In: Tyler, C.W., Ed., Human
Symmetry Perception and Its Computational Analysis, Lawrence Erlbaum Associates, New Jersey, 187-207.
[3] Tao, J. and Kuang, J.Y. (2007) A 3-D Point Set Registration Method in Reverse Engineering. Computers & Industrial
Engineering, 53, 270-276. http://dx.doi.org/10.1016/j.cie.2007.06.020
[4] Tuzikov, A.V., Colliot, O. and Bloch, I. (2003) Evaluation of the Symmetry Plane in 3D MR Brain Images. Pattern
Recognition Letters, 24, 2219-2233. http://dx.doi.org/10.1016/S0167-8655(03)00049-7
[5] Atallah, M. (1985) On Symmetry Detection. IEEE Transactions on Computers, 34, 663-666.
http://dx.doi.org/10.1109/TC.1985.1676605
[6] Wolter, J., Woo, T. and Volz, R. (1985) Optimal Algorithms for Symmetry Detection in Two and Three Dimensions.
The Visual Computer. http://dx.doi.org/10.1007/BF01901268
[7] Weyl, H. (1952) Symmetry. Princeton University Press.
[8] Miller, W. (1972) Symmetry Groups and Their Applications. Academic Press, London.
[9] Zabrodsky, H., Pelog, S. and Andavnir, D. (1995) Symmetry as a Continuous Feature. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 17, 1154-1166. http://dx.doi.org/10.1109/34.476508
[10] Zabrodsky, H. (1990) Symmetry VA Review. Tech. Rep. No. 90-16, CS Department, The Hebrew University of Jeru-
salem.
[11] Zabrodsky, H. and Wei nshal l, D. (1997) Using Bilateral Symmetry to Improve 3D Reconstruction from Image Se-
quences. Computer Vision and Image Understanding, 67, 48-57. http://dx.doi.org/10.1006/cviu.1996.0506
[12] Arun, K.S., Huang, T.S. and Blostein, S.D. (1987) Least-sSquares Fitting of Two 3-D Point Sets. IEEE Transactions
on Pattern Recognition and Machine Intelligence (PAMI), 9, 698-700.
[13] Umeyama S. (1991) Least-Squares Estimation of Transformation Parameters between Two Point Patterns. IEEE Tran-
sactions on Pattern Analysis and Machine Intelligence, 13, 376-380.
[14] Besl, P.J. and McKay, N.D. (1992) A Method for Registration of 3D Shapes. IEEE Transactions on Pattern Analysis
and Machine Intelligence, 14, 239-254. http://dx.doi.org/10.1109/34.121791
[15] Cheng, Y.Z. (1995) Mean Shift, Mode Seeking, and Clustering. IEEE Transactions on Pattern Analysis and Machine
Intelligence (IEEE), 17, 790-799.
[16] Besl, P. J. and McKay, N.D. (1992) A Method for Registration of 3D Shapes. IEEE Transactions on Pattern Analysis
and Machine Intelligence, 14, 239-254. http://dx.doi.org/10.1109/34.121791