 Journal of Computer and Communications, 2014, 2, 163-171 Published Online March 2014 in SciRes. http://www.scirp.org/journal/jcc http://dx.doi.org/10.4236/jcc.2014.24022 How to cite this paper: Yeh, J.-H., Joung, F.-J. and Lin, J.-C. (2014) CDV Index: A Validity Index for Better Clustering Quality Measurement. Journal of Computer and Communications, 2, 163-171. http://dx.doi.org/10.4236/jcc.2014.24022 CDV Index: A Validity Index for Better Clustering Quality Measurement Jian-Hua Yeh1, Fei-Jie Joung1, Jia-Chi Lin2 1Department of Computer Science and Information Engineering, Aletheia University, Taipe i, Chinese Taipei 2Department of Fashion and Administration Management, St. Johns University, Taip ei, Chinese Taipei Email: jhyeh@mail.au.edu.tw Received Novemb er 2013 Abstract In this paper, a cluster validity index called CDV index is presented. The CDV index is capable of providing a quality measurement for the goodness of a clustering result for a data set. The CDV index is composed of three major factors, including a statistically calculated external diameter factor, a restorer factor to reduce the effect of data dimension, and a number of clusters related punishment factor. With the calculation of the product of the three factors under various number of clusters settings, the best clustering result for some number of clusters setting is able to be found by searching for the minimum value of CDV curve. In the empirical experiments presented in this research, K-Means clustering method is chosen for its simplicity and execution speed. For the presentation of the effectiveness and superiority of the CDV index in the experiments, several traditional cluster validity indexes were implemented as the control group of experiments, in- cluding DI, DB I, ADI, and the most effective PBM index in recent years. The data sets of the expe- riments are also carefully selected to justify the generalization of CDV index, including three real world data sets and three artificial data sets which are the simulation of real world data distribu- tion. These data sets are all tested to present the superior features of CDV index. Keywords Cluster Validity Index; Unsupervised Learning; K-Means Clustering; Intra Cluster Compactness; Inter Cluster Dispersedness 1. Introduction In the past decade, the amount of data of the world has been grown and accumulated fast, which makes a severe challenge on effectively processing of data for the human beings. To process these fast-growing data properly and correctly, and transforming these data into useful contents, has drawn a lot of attention in the research fields. Machine learning [1] is one of the most important research domains to provide suitable algorithms for solving these problems. Machine learning algorithms analyze data sets and extract useful and interesting patterns, which then apply on the unknown incoming data for prediction. Since lots of machine learning algorithms are based on probabilistic or statistical models, these algorithms are also called statistical learning methods. The machine learning algorithms are widely-used in various domains, such as data mining, computer vision, natural language  J.-H. Yeh et al. processing, bioinfo rmatics, search engines, medical diagnosis, fraud detection, voice and hand-writing recogni- tion, games, and robotics. From the above application domains, we are able to categorize these domain problems into two major parts: supervised learning and unsupervised learning. For supervised learning problems, there exists a given data set to learn a mapping function from data to class label, when a new, unknown data comes, the mapping function out- put the prediction based on the given data. The data for supervised learning contains input and output part, also called feature data and class labels, and the class labels in the training data set is manually given. Regression and classification problems are frequently seen supervised problems. For unsupervised learning problems, the big- gest difference from supervised learning is on the absence of manually given class labels. The goal of unsuper- vised learning is generally on finding the underlying structure of data sets. Clustering is the best known unsu- pervised learning problem [2]. The clustering algorithm is a kind of method used to find closely related data items. Through a previously de- fined distance measure, this algorithm is able to group data items iteratively to form an underlying structure of the data. This structure, which is not explicitly shown, represents the similarity relationships among the data items. One of the widely known applications of clustering algorithms is the business decision support, such as searching for consumers of similar behavior patterns. By finding similar consumer groups, the company is able to effectively define suitable market strategy. Another widely known application of clustering algorithms is on bioinformatics domain, which finds similar gene patterns to deduce the homogeniety of biological pathway be- tween genes. Although there exist important applications of clustering algorithms, there are still several serious issues to solve, such as the quality control factor of the algorithms. Here the quality control factor is the proper clustering number for each data set to be clustered. The proper cluster number is the necessary parameter to be given in the whole clustering process. Different number of clusters setting will result in different clustering re- sults, which lead to different kinds of underlying structure of the data set. The different result of clustering may give a totally different interpretation of the data set, which will largely affect the marketing strategy. That is the reason why the cluster number plays an important role of the clustering algorithms. In this research, we propose a method to judge the quality of the clustering result. This judgment method is able to check whether the current clustering result is a suitable structure representation or not. The proposed method considers both the intra cluster and inter cluster relationships, with a properly defined penalty function, to form an numerical index for judgment. This index is called Cluster Discreteness Validity (CDV). With CDV, we are able to correctly find the underlying structure of data sets. The experiment results also showed that all the real world data sets and artificial ones are correctly processed through our method. Several traditional cluster validity indexes are also compared in this paper to show the superior property of CDV. 2. Related Works The clustering problem is one of the most well known research issues in the machine learning domain. The rea- son behinds the popularity of the clustering algorithms is on the widely used application domain. The clustering problem is to provide the solution for the following scenario: Suppose we have a set of data items, which con- sists of multiple dimensions of numerical data. If we want to organize these data items into several coherent and contrasted groups through an objective flow of process, each group contains data items of some sense of similar- ity, and different group of items are dissimilar in the same judgment standard. This objective flow of process is then called clustering. Though there are different kinds of clustering algorithms, the goal of these methods is to do the following process: If there exists a data set X, by deducing a partition matrix U(X), the data set is parti- tioned into K groups, as described below. { } 12 12 { ,,...}() , 1,2,...,,1,2,...,n , ,...,,1,2,..., ,1,2,..., , n kjkjj k ni ij Xxxxis a data setDeduce a Knpartition matrixUX UuwherekKjuisthe membership valueofxto cluster C The set ofcluster CCCCCiK CCfor iKj ϕ ϕ = × == = = ≠= = = 1 1,2,..., , K i i Ki j CX = = ≠ = (1)  J.-H. Yeh et al. In Equation (1), the value of ukj is either 0 or 1 for traditional crisp clustering problems. From the above defi- nition, we can easily catch that the value of K directly affect the cell values inside the matrix U. Accompanying with the decision of K value, the quality of U matrix is obviously affected by K. From this observation, the two major issues of clustering problem has revealed, one is the decision of number of cluster, the other is the cluster quality. In the past researches, the decision of number of clusters is closely related to the cluster quality. The reason why the two issues are closely related is that the reasonable number of cluster will deduce the reasonable clustering result. For the real world applications, reasonable clustering result is the underlying structure found by clustering algorithm which is able to be easily judged and accepted by human beings. This shows the importance on the number of clusters researches. Traditionally, the number of clusters researches located on developing a good cluster validity index, which measures the goodness of a clustering result. The measurement of the good- ness of a clustering result generally consists of two major parts, the intra cluster compactness and inter cluster dispersedness. For the intra cluster compactness, a better number of clusters will get a higher cluster density, which represents the closer relationship of the data items. For the inter-cluster discreteness, a better number of clusters will result in a better partition of clusters. The commonly found cluster validity indexes in the literature are Davies-Bouldin Index (DBI) [3], Dunn Index (DI) [4], Alternative Dunn Index (ADI) [5], and PBM index [6]. Davis-Bouldin Index [3] was proposed by David L. Davis and Donald W. Bouldin, which is a formula to measure the clustering results. The DBI index focuses on the ratio of within-cluster scatter and between-cluster separation, which is similar to the concept of degree of intra cluster and inter cluster relationships. The intra cluster density is defined by the average distance of each member to the center of the cluster, as shown in Equa- tion (2). { } 1 ,2 1 ,1 ,, , 1, () 1max i qq iq i xC pt t ij tisjs s Kiq jq jj i iij t S xz d zz SS DBI Kd ∈ = ≠ = = − = − + = ∑ ∑ ∑ (2) In Equation (2), Si,q is the sum of distance from the members to the center of cluster i, with a q-th root of the value of the q-th moment. The intra cluster distance dij,t is defined by the order-t Minkowski distance [7] be- tween cluster i and j. The smaller DBI value means the denser intra cluster property and larger inter cluster dis- tances, which leads to a better clustering result. Dunn Index [4] was proposed by J. C. Dunn in 1974. Similar to the DBI index, the DI index measures the quality of clustering result. The goal of DI index is the same with other cluster validity indexes which tries to find a good intra cluster and inter cluster relationships. The DI index is defined as follows: 1 1, 1 (, ) min minmax'( ) ij in jnji kn dcc DI dk ≤≤≤ ≤≠ ≤≤ = (3) In Equation (3), the variable n is the number of clusters and d(·, ·) is the distance function. The function d'(k) calculates the average distance from cluster elements to the center of cluster k. The DI index calculates the ratio of inter cluster and intra cluster relationships, the larger value of DI index means a better clustering result. Alternative Dunn Index [5] is a variation of DI index, the difference between DI and ADI is on the in- ter-cluster distance measurement. The DI index tries to find the minimum distance between elements belonging to different clusters, while the ADI index tries to replace this calculation with the triangular inequality 1 1, 1 (,) (,) min minmax'( ) ij jj injnjikn dxvdx v ADI dk ≤≤≤ ≤≠ ≤≤ − = (4)  J.-H. Yeh et al. In Equation (4), the variable vj represents the center of cluster j, the rest parts of the equation remain the same with DI index. Similarily, a larger ADI index value indicates a better clustering result. PBM Index [6] was proposed by Pakhira, Bandyopadhyay and Maulik in 2003. The design of PBM index is based largely on intra cluster density, with a penalty score multiplication on inter cluster distance. This design claims that when the number of clusters is not properly set, the clustering result will be incorrect and the intra and inter cluster relationships will be abnormally presented. The PBM index utilizes the abnormalilty of the re- lationships of clusters to define a penalty to worsen the index value by multiplication of the penalty to the intra cluster density. The PBM index is defined as follows: 1 1 1 ,1 1 , , max K K K Kk k n kkj jk j kjj k K K ij ij E PBM D KE whereKis the numberofclustersEE suchthatEuxz uis the membership value ofxto clusterC and Dzz = = = =⋅⋅ = = − = − ∑ ∑ (5) In Equation (5), the variable n is the total number of points in the data set, U(X) = [ukj]K × n is a partition matrix for the data and zk is the center of cluster k. The objective is to maximize this index in order to obtain the actual number of clusters. 3. Proposed Method The goal of this research is to find a more generalized cluster validity index under hard clustering environment in compared with those traditional indexes. This proposed index is able to solve the incorrect prediction found in the previous indexes, while considers the data trend with high feature dimensionality recently. In this section, a cluster validity index called CDV (Cluster Discreteness Validity) index is proposed, followed with the descrip- tion of the index design, to express the suitability of the index under different kinds of data environments. The design of the proposed CDV index is shown in Equation (6) as follows: 1 1 22 , ,dim , 22 11 k C kj jk j kk k kjj k D kk k kD k ux z RC whereCisthe size ofclusterkand uis the membership valueofxto cluster C ECwhereD is theension ofdataand MEC = − = = =+=+ ∑ (6) In Equation (6), K is the number of clusters, Rk represents the average radius of cluster Ck, Mk is calculated by dividing the expectation value of average compensation of cluster boundary by Ek, while Ek is the average ap- portionment in each data dimension of the cluster. The last part of the CDV index is designed to conquer the unreasonableness of the traditional cluster validity index design. In this case, a punishment factor should be added into the index in order to compensate the defect of density or radius factor in the index. 4. Experiments and Discussions In this research, 6 independent data sets are adopted to show the effectiveness of the proposed method. There are  J.-H. Yeh et al. 3 real world data sets of them, and the others are artificial data sets. In the comparison experiments, we used the traditional cluster validity indexes with these data sets to find the suitable cluster number recommended by the indexes including DI, DBI, AD I , and PBM. The K-Means [8] method is selected as the clustering method for the experiments. The reason to adopt K-Means clustering is the simple nature of the algorithm. K-Means runs fast, which is suitably for observation of the experiments. 5. Data Sets There are 3 out of 6 data sets of real world data selected, they are Iris, Cancer, and Wine data sets. • Iris data: This data set keeps the physical measurement results of different kinds of iris, which is downloada- ble online from [http://archiv e.ics .uci.edu /ml/datasets/Ir is]. Each data record contains 4 attributes, which are sepal length, sepal width, petal length, and petal width measuring in centimeters [9]. The target class re- presents the species of iris. Three different kinds of iris are recorded, they are Setosa, Versicolor, and Vir- ginia. There are 150 data records of each class. The class Setosa is completely linear separable of the other class. Most of the cluster validity index reported the result of two clusters of this data set in the literature [10,11]. • Cancer data: The Cancer data set represents the Wisconsin Breast Cancer data, which is downloadable online from [http://archive.ics.uci.edu/ml/datasets/ Breas t+Cance r]. In this data set, each data record consists of 9 attributes, which correspond to clump thickness, cell size uniformity, cell shape uniformity, marginal adhe- sion, single epithelial cell size, bare nuclei, bland chromatin, normal nucleoli, and mitoses. There are two classes in this data: malignant and benign. The classes of this data set are known to be linearly separable. The number of data records is 286. • Wine data: The Wine data set represents the results of a chemical analysis of wines grown in a specific area of Italy, which is downloadable online from [http://arch ive. ics.uci. edu/ml/datasets/W in e]. In this data set, each data record contains 13 attributes of various chemical analyses, and there are 3 target classes to predict. The number of data records is 178. Besides the real world data sets, several artificial data sets are prepared for the experiments. These artificial data set are used to depict possible data patterns of the real world which cannot be found in the public data sets. The data sets are named by the number of clusters and the dimension of the data. For example, the data set Cir- cular: 6:2 indicates that the data distribution is in a circular shape, there are 6 clusters in the data, and the data is two-dimensional. The data set Spherical: 4:3 represents a spherical data distribution with 4 clusters and three dimensional data. The data sets used here are Circular: 6:2, Circular: 9:2, and Spherical: 4:3. Figures 1-3 present the data distributions of these data sets. 6. Experiment Results Through K-Means clustering, the selected data sets are clustered for several times because the output of K-Means clustering is greatly affected by the initial random centers. In our experiments, K-Means clustering runs multiple times for a single data set, and the output with the minimal intra cluster density is treated as the correct cluster result. This principle is applied to all the cluster validity indexes in the experiments. For the fair- ness and integrity of the experiments, the data records are all normalized before clustering begins. For the range of the number of clusters used in the K-Means clustering, according to the literature [12], the maximum number of clusters should not exceeds when there are n data records. Therefore, the upper limit for clustering test of n-element data set is . Each of the above 6 data sets is clustered by K-Means and the cluster quality is verified by proposed CDV index. According to the different number of clusters k, the different CDV value is calculated. With the CDV suggestion proposed in the last section, the optimal number of clusters suggested for Circular:6:2, Circular:9:2, and Spherical:4:3 data sets is 6, 9, and 4, respectively. The suggestions are correctly found by CDV. With the accurate calculation of artificial data sets, the real data sets Iris, Cancer, and Wine were tested consequently. The number of clusters results suggested by CDV index is 3, 3, 2, respJectively, which are all correct recommendations by CDV. Similarly, the optimal number of clusters suggested for Iris, Cancer, Wine data sets is 3, 2, and 3, re- spectively, which are all correct recommendations by CDV. Next we set up several control groups of experiments as comparisons. The DI, DBI, ADI, and PBM indexes are implemented to find their best suggestions with the same data sets and K-Mean clustering method. Table 1 shows the number of clusters results found by various cluster validity index under different data sets. In this 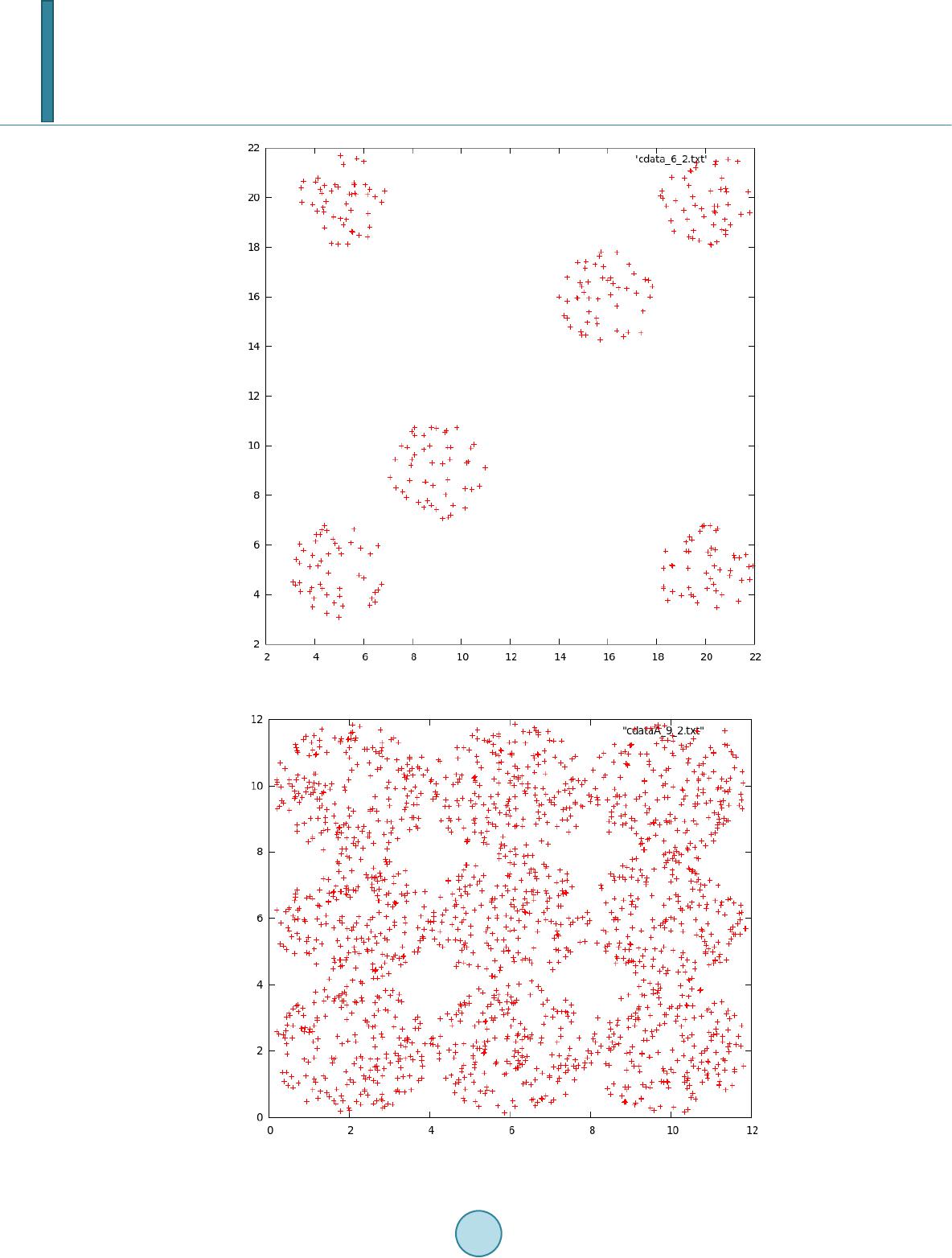 J.-H. Yeh et al. Figure 1. The data distribution of artificial data set Circular: 6:2. Figure 2. The data distribution of artificial data set Circular: 9:2.  J.-H. Yeh et al. Figure 3. The data distribution of artificial data set Spherical: 4:3. Table 1. The number of clusters results found by various cluster validity index under different data sets. Data set Actual # # clusters obtained DBI DI ADI PBM CDV Circular: 6:2 6 6 4 4 6 6 Circular: 9:2 9 9 9 10 4 9 Spherical: 4:3 4 4 4 4 4 4 Iris 3 2 2 2 3 3 Cancer 2 2 3 2 2 2 Wine 3 2 19 12 2 3 table, each column represents the real number of cluster and those calculated by DI, DBI, ADI , PBM, and CDV index. As we can found in this table, CDV provided the most accurate number of clusters prediction, DI index failed on Iris and Cancer data sets, DBI index failed on Iris, Wine and Circular: 6:2, and ADI index failed on Iris and Wine data sets. Recently, the most correct predictor PBM was also failed in Wine and Circular: 9:2 data sets. Table 2 integrates the results calculated by proposed CDV index for all data sets. The bold face numbers are the number of clusters suggestions made by CDV index. From this table, it is easy to observe that CDV has the ability to provide accurate judgments on number of cluster for each data set, that is, the CDV index is able to find the most suitable partitions for every data set. Since the PBM index is the most accurate cluster validity in- dex in recent years, we compared the PBM results with CDV index on the data sets used in this paper to discuss  J.-H. Yeh et al. Table 2. The experiment results calculated by proposed CDV index for all data sets. # Data set Iris Cancer DBI DI ADI PBM CDV DBI DI ADI PBM CDV 2 0.437 0.416 0.228 0.757 0.298 0.781 0.148 4.34E−05 1.450 0.660 3 0.683 0.175 7.99E−04 0.995 0.289 1.549 0.169 0 1.043 0.742 4 0.817 0.100 1.28E−04 0.815 0.298 1.743 0.056 3.12E−17 0.765 0.661 5 0.958 0.054 1.46E−04 0.631 0.304 1.685 0.058 3.20E−17 0.645 0.727 6 1.078 0.086 1.50E−04 0.484 0.294 1.679 0.060 6.68E−17 0.454 0.770 7 1.170 0.086 1.82E−04 0.447 0.310 1.615 0.066 0 0.384 0.806 8 1.176 0.061 1.50E−04 0.291 0.314 1.618 0.062 0 0.372 0.831 9 1.109 0.120 2.50E−04 0.363 0.360 1.637 0.116 0 0.232 0.904 10 1.162 0.106 8.53E−04 0.315 0.369 1.716 0.062 0 0.219 0.847 11 1.124 0.074 3.97E−04 0.253 0.349 1.639 0.067 0 0.183 0.812 12 1.089 0.074 5.54E−04 0.232 0.370 1.716 0.059 0 0.187 0.789 13 1.144 0.082 5.61E−04 0.243 0.392 1.698 0.060 0 0.128 0.793 14 1.137 0.082 4.64E−05 0.189 0.399 1.719 0.070 0 0.125 0.837 15 1.355 0.093 4.93E−04 0.180 0.421 1.730 0.060 0 0.109 0.817 16 1.241 0.085 1.94E−04 0.173 0.417 1.674 0.072 0 0.109 0.878 17 1.147 0.045 3.75E−04 0.172 0.423 1.589 0.070 0 0.096 0.886 18 1.173 0.097 3.23E−04 0.142 0.423 1.645 0.065 0 0.102 0.872 19 1.228 0.088 1.94E−04 0.143 0.448 1.588 0.070 0 0.086 0.864 20 1.276 0.099 2.14E−04 0.132 0.463 1.658 0.070 0 0.074 0.899 the feature of judgment of number of clusters, as shown in Table 1. From the observations of Table 1, it is found that though the PBM index made correct suggestions on most cases, it failed on the Circular: 9:2 case with a strange prediction result. The Circular: 9:2 is a Sudoku-like type of data distribution, which can be easily found in human society. The PBM index suggestion biased the number of clusters from correct 9 groups to 4, which is far from the correct answer. 7. Conclusions and Future Works Clustering is an unsupervised machine learning algorithm. The main characteristics of clustering problem is that the group tendency of data is not known in advance, that is, the underlying structure of data is not understood before the clustering process. Therefore, the number of cluster parameter provided for the clustering algorithm plays the critical role during the whole process. In the clustering process, or called exploratory data analysis, the pattern of a data set usually consists of a set of multi-dimensional vectors. By adopting clustering process, these vectors are organized into several contrasted groups, the members of the same group represents a certain degree of similarity, while the members from different groups show contrasted features. In this research, a cluster validity index called CDV index is proposed. We explain the mathematical analysis for the design of CDV index. The CDV index is also used as a comparison with other existing indexes on sever- al data sets including real word cases and artificial ones. The design of CDV is similar to other indexes, which focuses on certain boundary condition to provide the suggestion. That is, the CDV index is able to cope with ex- isting optimization algorithm to search for the best number of clusters. The CDV index consists of three factors  J.-H. Yeh et al. of calculation, they are cluster radii, number of partitions, and a punishment factor based on the number of parti- tions. These factors are multiplies together to find the best number of clusters suggestion. In the experiments, the K-Means clustering method was adopted due to the simple and fast nature of the algo- rithm. The clustering results from K-Means method were used to calculate the various kinds of cluster validity indexes in order to show the effectiveness of CDV index over other ones. The data sets used in the experiments include both real world data and artificial data. The experiment results are believed to have certain degree of preciseness and reliability which indicate the CDV index is by far the most effective design of cluster validity index. References [1] Mitchell, T.M. (1997) Machine Learning. 1st Edition, McGraw-Hill, Inc., New York. [2] Bishop, C.M. (2006) Pattern Recognition and Machine Learning (Information Science and Statistics), Springer-Verlag New York, Inc., Secaucus. [3] Davies, D.L. and Bouldin, D.W. (1979) A Cluster Separation Measure. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1, 224-227. http://dx.doi.org/10.1109/TPAMI.1979.4766909 [4] Dunn, J.C. (1973) A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clus- ters. Journal of Cybernetics, 3, 32-57. http://dx.doi.org/10.1080/01969727308546046 [5] Shafi, I., Ahmad, J., Shah, S.I., Ikram, A.A., Khan, A.A. and Bashir, S. (2010) Validity-Guided Fuzzy Clustering Evaluation for Neural Network-Based Time-Frequency Reassignment. EURASIP Journal on Advances in Signal Processing, 2010, Article ID: 636858. http://dx.doi.org/10.1155/2010/636858 [6] Pakhira, M.K., Bandyopadhyay, S. and Maulik, U. (2004) Validity Index for Crisp and Fuzzy Clusters. 37, 487-501. [7] Wikipedia. Minkowski Distance. http://en.wikipedia.org/wiki/Minkowski_distance [8] Macqueen, J.B. (1967) Some Methods for Classification and Analysis of Multi-Variate Observations. Proceedings of the Fifth Berkeley Symposium on Math, Statistics, and Probability, Vol. 1, University of California Press, 281-297. [9] Fisher, R.A. (1936) The Use of Multiple Measurements in Taxonomic Problems. Annals of Eugenics, 7, 179-188. http://dx.doi.org/10.1111/j.1469-1809.1936.tb02137.x [10] Bezdek, J.C. and Pal, N.R. (1998) Some New Indexes of Cluster Validity. Transactions on Systems, Man, and Cyber- netics—Part B, 28, 301-315. http://dx.doi.org/10.1109/3477.678624 [11] Kothari, R. and Pitts, D. (1999) On Finding the Number of Clusters. Pattern Recognition Letters, 20, 405-416. http://dx.doi.org/10.1016/S0167-8655(99)00008-2 [12] Pal, N.R. and Bezdek, J.C. (1995) On Cluster Validity for the Fuzzy c-Means Model. IEEE Transactions on Fuzzy Sys- tems, 3, 370-379. http://dx.doi.org/10.1109/91.413225
|