Journal of Computer and Communications, 2014, 2, 148-156
Published Online March 2014 in SciRes. http://www.scirp.org/journal/jcc
http://dx.doi.org/10.4236/jcc.2014.24020
How to cite this paper: Li, H.-B. and Wong, M.-L. (2014) Knowledge Discovering in Corporate Securities Fraud by Using
Grammar Based Genetic Programming. Journal of Computer and Communications, 2, 148-156.
http://dx.doi.org/10.4236/jcc.2014.24020
Knowledge Discovering in Corporate
Securities Fraud by Using Grammar Based
Genetic Programming
Hai-Bing Li, Man-Leung Wong
Department of Computing and Decision Sciences, Lingnan University, Hong Kong, China
Received Novemb er 20 13
Abstract
Securities fraud is a common worldwide problem, resulting in serious negative consequences to
securities market each year. Securities Regulatory Commission from various countries has also
attached great importance to the detection and prevention of securities fraud activities. Securities
fraud is also increasing due to the rapid expansion of securities market in China. In accomplishing
the task of securities fraud detection, China Securities Regulatory Commission (CSRC) could be fa-
cilitated in their work by using a number of data mining techniques. In this paper, we investigate
the usefulness of Logistic regression model, Neural Networks (NNs), Sequential minimal optimiza-
tion (SMO), Radial Basis Function (RBF) networks, Bayesian networks and Grammar Based Genet-
ic Programming (GBGP) in the classification of the real, large and latest China Corporate Securities
Fraud (CCSF) database. The six data mining techniques are compared in terms of their perfor-
mances. As a result, we found GBGP outperforms others. This paper describes the GBGP in detail in
solving the CCSF problem. In addition, the Synthetic Minority Over-sampling Technique (SMOTE)
is applied to generate synthetic minority class examples for the imbalanced CCSF dataset.
Keywords
Knowledge Discovering; Rule Induction; Token Competition; SMOTE; Corporate Securities Fraud
Detection; Grammar-Based Genetic Programming
1. Introduction
In the US, financial analysts have been confirmed to contribute to corporate fraud detection. Effective external
monitoring can increase investors’ confidence, which is crucial to the functioning of any capital market [1]. It is
also important for China’s securities market, as corporate fraud can impede China’s economic development
since it has serious consequences to stakeholders, employees and society [1]. In recent years, corporate securi-
ties fraud detection becomes a hot spot domain in finance and there is a wave of research papers that have stu-
died effective policies to detect and reduce fraud.
In China, the Securities Regulatory Commission (CSRC) serves as the main regulator of securities markets in
China, which devotes to investigate the potential violations of securities regulations and make different en-

H.-B. Li, M.-L. Wong
149
forcement actions to those fraudulent corporations that have violated related laws. Any of the enforcement ac-
tions from the CSRC will affect the stock price of the firm, even result in bankruptcy [2]. Prior studies on the
causes of securities fraud focused on different types of determinants, such as agency problems, business pres-
sures and corporate governance [3,4]. There is a large related dataset about China’s listed companies collected
based on these determinants for this study, in order to find out corresponding relationships to detect whether a
company is fraudulent or non-fraudulent. In this paper, we aim to evaluate several data mining techniques for
the large and latest China Corporate Securities Fraud (CCSF) dataset. We also highlight the advantages of using
SMOTE as the technique for the imbalanced data manipulation.
The main objective of this study is to contribute to identifying the factors of the company in assessing the li-
kelihood of fraud by applying different statistical and Artificial Intelligence (AI) data mining techniques. AI da-
ta mining techniques have the theoretical advantage that they do not use arbitrary assumptions on the input va-
riables [5]. The models are built based on the data itself and used for the data. In this study, six data mining
techniques are tested for their applicability in corporate securities fraud detection, which are Logistic regression
model, Neural Networks (NNs), Sequential minimal optimization (SMO), Radial Basis Function (RBF) net-
works, Bayesian networks and Grammar Based Genetic Programming (GBGP). The six techniques are com-
pared in terms of their classification accuracy. As a result, we found GBGP outperforms others. Thus the detail
of using GBGP will be comprehensively discussed in this study.
The rest of the paper is organized as follows. Section 2 is the background and previous work. Section 3 de-
scribes the utilization of the GBGP approach. Section 4 provides the experimental results and evaluations. Sec-
tion 5 discusses the conclusion and future work of the project.
2. Background and Previous Work
The China Securities Regulatory Commission (CSRC) has the similar powers and operations to SRC in the U.S.
They investigate and take enforcement actions to listed corporations if their securities frauds are detected and
proved. [6] examined these enforcement actions to explain whether the ownership and governance structures of
corporations have impacts to commit fraud. The authors concluded that the proportion of outside directors, the
tenure of the chairman and number of board meetings are related factors to commit fraud. [7] investigated en-
forcement actions from the viewpoint of the fraudulent firms rather than what factors lead up to fraud. They
found that many of these firms have problems with published financial statements and irregular reports, such as
inflated profit, false statements and major failure to disclose information, which are the common problems iden-
tified by the CSRC.
Considering the laws of federal securities, [8] examined the four attributes that might associated with the
fraud including the number of defrauded investors, assets size, losses and financial distress of the firm. The au-
thors concluded that only financial distress has a significant impact on the presence or absence of an enforce-
ment action. In general, since the result of the enforcement action is either yes or no (i.e. 1 or 0), it is more rea-
sonable to use bivariate probit model as the learning method to analysis the data.
Normal analysing methods may not discover many potential relationships. Therefore a lot of researchers have
studied concept learning from data using genetic algorithms in classification problems. In [9], the authors eva-
luated GP in classification problems, and found that the more training time results in more accurate of the
trained model by using Genetic Programming (GP) method. In addition, different runs may generate different
novel models but are still able to solve the same problems. [10] developed a rule learning system that demon-
strated the power and flexibility for knowledge discovery in real-life medical problems. Moreover, the authors
applied token competition for learning multiple rules and reducing training time.
Except for evolutionary-based techniques, other data mining techniques are also widely used in classification
problems. [5] evaluated the effectiveness of Decision Trees, Neural Networks and Bayesian Belief Networks in
detecting and identifying the factors associated with fraudulent financial statements (FFS). In terms of their per-
formance, the Bayesian Belief Network model outperforms others considering about accuracy. [11] developed
fuzzy neural network (FNN) for corporate fraud detection and compared the performance of FNN with tradi-
tional neural networks and logistic regression.
3. Research Methodology
Identifying corporate securities fraud can be regarded as a typical classification problem. Six methods are em-

H.-B. Li, M.-L. Wong
150
ployed in this study, which are Logistic regression, Neural Networks (NNs), Sequential minimal optimization
(SMO), Radial basis function (RBF) networks, Bayesian networks and Grammar-Based Genetic Programming
(GBGP). Among these methods, GBGP will be introduced comprehensively.
3.1. Introduction to Grammar Based Genetic Programming (GBGP)
Comparing GBGP [12,13] with traditional GP [14], the concept of grammar is employed, which is used to con-
trol the structure during the evolutionary process. GBGP supports logic grammars, context-free grammars
(CFGs) and context-sensitive grammars (CSGs) [15] to generate tree-based programs. The suitable grammar is
designed for solving a particular problem. In this stud y, the designed grammar is shown in Table 1 for the rule
learning in CCSF dataset. In order to have a better understanding about the designed grammar, a simple example
in Table 2 can be used to illustrate the idea of using grammars. GBGP can ensure the structures of evolved rules
are valid during the evolution.
Table 2 is an example of a context-free grammar. Expression is the start symbol. The items with capital let-
ters are the non-terminal symbols, and others are the terminal symbols. Each statement indicates a rule with the
form α → β to show how a non-terminal symbol is expanded to another non-terminal or terminal symbol. The
representation of individual in GBGP is a tree-based structure. The root node of an individual is the start symbol
of the grammar. Figure 1 is the example of an individual in GBGP, which is generated by using grammar in
Table 2.
3.2. System Flows
Figure 2 shows the standard flowchart of the GBGP algorithm [10]. Firstly, the system loads the grammar and
Table 1. A grammar for CCSF problem.
Rule -> ifFirmAntes and FinancialAntes and GovernanceA ntes, then Consq.
FirmAntes ->Location and Industry and Market and ABshare
FinancialAntes->Asset and ShortTerm and Operating and LongTerm
andEarning and RiskLevel and ROE and HDividend and Dividend
GovernanceAntes ->NOS and NOE and ChairCEO and NOM
Location ->any | Location_descriptor
Industry -> any | Industry_descriptor
Market -> any | Market _descriptor
ABshare -> any | ABshare _descriptor
Asset -> any | Asset_descriptor
ShortTerm -> any | ShortTerm_descriptor
Operating -> any | Operating_descriptor
LongTerm -> any | LongTerm_descriptor
Earning ->any| Earning_descriptor
RiskLevel -> any | RiskLevel_descriptor
ROE -> any | ROE_descriptor
HDividend ->any | HDividend_descriptor
Dividend -> any | Dividend_descriptor
NOS -> any | NOS_descriptor
NOE -> any | NOE_descriptor
ChairCEO -> any | ChairCEO_descriptor
NOM -> any | NOM_descriptor
Location_descriptor -> location = location_erc
Industry_descriptor -> industry = industry_erc
Market_descriptor -> market =market_erc
ABshare_descriptor -> abshare = abshare_erc
Asset_descriptor ->asset between asset_erc asset_erc
ShortTerm_descriptor ->shortterm between sh_erc sh_erc
Operating_descriptor ->operating between ope_erc ope_erc
LongTerm_descriptor ->longterm between long_erc long_erc
Earning_descriptor-> earning between earn_erc earn_erc
RiskLevel_descriptor ->risklevel between risk_erc risk_erc
ROE_descriptor -> roe between roe_erc roe_erc
HDividend_descriptor -> hdivident = hdivident_erc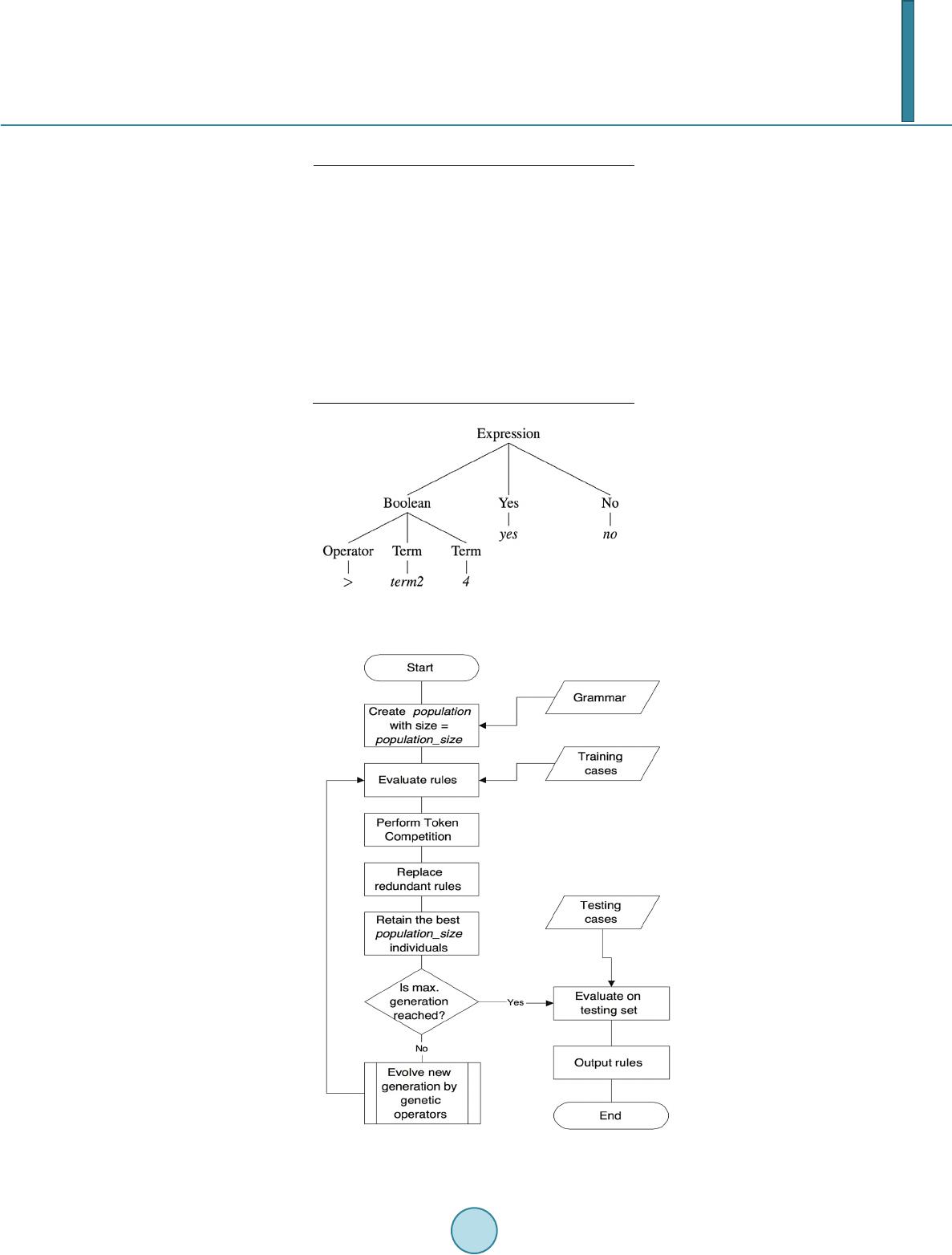

H.-B. Li, M.-L. Wong
151
Table 2. A simple example of a context-free grammar.
Expression → Boolean Yes No
Boolean → Operator Term Term
Boolean → true | false
Term → term1 | term2 | term3
Term → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Operator → = | >= | <= | > | <
Yes → yes
No → no
Figure 1. An individual program in GBGP represents if
the value of ter m2 > 4 then yes, otherwise no.
Figure 2. A flowchart of the GBGP system.

H.-B. Li, M.-L. Wong
152
then creates the initial population with user-defined size.
The initial population is randomly generated according to the grammar. Each individual represents one rule,
which will be evaluated by a fitness function to calculate a score (accuracy). The fitness function is described in
Section 3.5. Secondly, token competition is applied to maintain the good rules and diversity of the population.
The detail about token competition is described in Section 3.6. Thirdly, if the stopping criterion is not reached,
the new individuals are evolved by crossover and mutation operators, which are described in Section 3.4. The
evolved rules will be finally evaluated by the testing instances until the stopping criterion is reached.
3.3. Grammar
The general format of a rule is defined as “IF conditions, THEN results”. The conditions part involves a set of
descriptors, which are divided into three major groups and shown in Table 1. The first group is related to firm
basic characteristics that includes location: where the firm is located; industry : which industry that the firm be-
longs to; market: the firm is listed in Shanghai or Shenzhen stock market; ABshare: the firm is listed in A share
or B share. The second group concerns the financial characteristics, which are assets: indicates the current asset
of the company; shortterm: represents the short term solvency of working capital to total assets ratio; operating:
indicates the fixed asset turnover capacity; longterm: is a radio of liabilities to total assets of the firm; earning: is
the return on asset; risklevel: indicates the total leverage of the firm; roe: stands for return on equity, represents
earnings per share; hdividend: whether the firm distributes dividend (yes or no); dividend: indicates how much
dividend the firm distributes. The third group is about the governance features, which include nos: is the number
of shareholders; noe: is the number of employees in the firm; cha irCEO : whether the chairman of the board and
CEO is the same person; nom: is the number of board meetings per year. The descriptors are selected based on
the previous work in Section 2. The results part has only one descriptor that shows the firm is fraudulent or not.
3.4. Genetic Operators
After initializing the individuals to form a population at the first generation, the parental individuals are selected
by using ranking selection method in terms of their fitness values [16]. Crossover and mutation operators will
produce new individuals from the selected parents. In this process, crossover operator swaps the subtree from
two different parents. Mutation is able to alter a non-terminal variable, changes the value of the mutated variable
randomly in terms of the designed grammar, or turns the attribute into “any” if the attribute will not be consid-
ered in the rule [10,13].
3.5. Fitness Evaluation
The fitness function measures the overall classification accuracy, which is the percentage of correctly classified
examples for both classes to the total number of training examples. The possible outcomes for binary classifica-
tion are shown in Table 3, and in this fraud detection problem, the minority class (fraudulent example) is the
positive class. The overall accuracy is defined by Equation (1).
TP TN
Accuracy TPFNFP TN
+
=
+ ++
(1)
3.6. Token Competition
In addition to obtain high accurate individuals (classifiers), the token competition technique [17] is employed to
maintain the diversity of the population. In token competition, each instance in the training samples is a token
(score). If an individual (rule) classifies the instance correctly, then it will get one token and compare with other
Table 3. Four outcomes of binary classification.
Classified as True Classified as False
Actual is True True Positive (TP) False Negative (FN)
Actual is False False Positive (FP) True Negative (TN)

H.-B. Li, M.-L. Wong
153
rules that can also classify the same instance. The rules with no or few tokens are removed in order to provide
positions for good or strong rules come into the population. Therefore, the evolved population will have a set of
strong individuals eventually [17]. To apply the token competition for each individual is just to multiply the
original fitness value with ratio t. where t is the number of tokens that the rule has obtained divided by the ideal
number of tokens (i.e. number of training examples), which is shown in Equation (2).
_*updatedfitnessfitness t=
(2)
4. Experiments and Results Analysis
4.1. Data Description
The original China Corporate Securities Fraud (CCSF) database contains records of corporations with their firm,
financial, governance and trade characteristics. The variables are selected on the basis of the relative literatures
that have been discussed in Section 2. Moreover, including more attributes may provide more interesting infor-
mation of the fraudulent firms for the system to learn. The original database has 21,396 instances with 25 attri-
butes for all listed firms from 1998 to 2011. Each instance with more than 20 missing values in these 25 attri-
butes is directly removed. Moreover, there are 7 attributes about trade characteristics are removed since more
than two third firms have no such trade data. The final dataset has 18,373 records with 18 attributes. The re-
maining missing values can be represented by “any” in the grammar.
Table 4 shows the variables and corresponding brief definitions used in the GBGP rule learning system.
4.2. Data Preprocessing
The original CCSF database is highly imbalanced with 5.8% fraudulent and 94.2% non-fraudulent examples.
Without considering the imbalance prior, the classifier(s) will always have biased results to the majority class.
Table 4. Definition of variables.
Variable Type Definition
industry char The industry that the firm belongs to
abshare char A-share or B-share market
market char Listed in Shanghai or Shenzhen
location char The location of the firm
asset float The asset of the firm
shortterm float Working Capital to Total Assets Ratio
operating float Fixed Asset Turnover
longterm float Liabilities to Total Assets Ratio
earning float Return on Asset
risklevel float Total Leverage
roe float Earnings Per Share
hdividend char Whether the firm pay dividend
dividend float The dividend paid to shareholders
shareholders int The number of shareholders
employees int The number of employees
chairCEO char The chairman and CEO are the same
meeting int The number of boards’ meeting
type char The firm commits fraud or not

H.-B. Li, M.-L. Wong
154
Such classifiers are not useful, as the performance could be very low for the objectives [18]. A number of ap-
proaches have been introduced to address on the imbalanced problems. One of the most popular techniques is to
resample the training data.
This paper applies synthetic minority over-sampling technique (SMOTE) for a variety of reasons. First, the
standard SMOTE is very simple to implement in practice. Second, empirically, SMOTE has shown to perform
well against random oversampling techniques in a lot of experiments [18,19]. Third, the synthetic examples are
generated in less application-oriented manner. That is the new examples are operated in feature space rather than
data space [19]. Therefore, it can be widely applied in imbalanced datasets applications.
4.3. Experiment Setup
The parameters setting that control the rule learning system are shown in Table 5.
The values for the parameters setting that control SMO and neural networks are shown in Table 6. All expe-
riments applied 10-fold Cross-validations to evaluate the performance of different method.
4.4. Results and Evaluations
The performance of Logistic Regression model, Neural Networks, SMO, RBF network, Bayesian networks and
rule learning system (GBGP) is shown in Table 7. TP rate (yes) is the true positive rate for fraudulent firms,
which is calculated by Equation (3).
_( )/()TPrateYesTPTPFN= +
(3)
TP rate (no) is the true negative rate for non-fraudule n t firms, which is calculated by Equation (4).
_( )/()
TPrate NoTNTNFP= +
(4)
The result shows that Logistic Regression model, Neural Networks, SMO and Bayesian networks are able to
classify the non-fraudulent firms, especially for Bayesian networks, which outperform other techniques in terms
Table 5. The parameters and values for the system.
GBGP
Parameter Value
Number of production rules 57
Population size 20
Max. no. of generations 100
Use elitism yes
Keep parent yes
Use token competition yes
Crossover rate 0.8
Mutation rate 0.3
Table 6. The parameters and values for NNs and SMO.
Neural Networks SMO
Parameter Value Parameter Value
Learning rate
Momentum value
No. hidden layers
weight update
Training epochs
0.3
0.2
1
BP.
500
kernel function
complexity
Tolerance Rate
exponent value
Polykernel
1
0.001
1

H.-B. Li, M.-L. Wong
155
of accuracy. However, they perform poorly in fraudulent firms detection. The possible reason is that, the CCSF
dataset is hard to build models by using these techniques. In addition, since it contains many noisy examples,
which may be further rescaled by SMOTE. For the variables that will not be learnt in the rule can be represented
by the term “any” in GBGP method. Therefore, it performs well in both classes. The comparison between
GBGP with other models is shown in Table 8.
In Table 8, Acc (yes) is the classification accuracy for fraudulent firms, and Acc (no) is the classification ac-
curacy for non-fraudulent firms. Diff. devotes the average difference between the performances of GBGP with
the compared approach. S.D. presents the stand derivation and t-stat is a value to test if the average difference is
significantly different from zero or not.
From Table 8, the GBGP outperforms Logistic regression, NNs and SMO in both classes significantly. The
GBGP performs better in classifying non-fraudulent firms significantly compared to RBF network, and outper-
forms Bayesian networks in classifying fraudulent firms significantly.
5. Conclusions and Future Work
In this study, we have compared the performance of six different approaches in solving the China Corporate
Securities Fraud (CCSF) problem. We found the GBGP outperforms Logistic regression model, back-propaga-
tion neural networks, SMO, RBF networks with Gaussian function and Bayesian networks in terms of accuracy.
Table 7. The performance table in CCSF dataset.
TP rate (Yes) TP rate (no)
Logistic Regression 0.4083 ± 0.0451 0.7473 ± 0.0171
Neural Networks 0.3123 ± 0.0667 0.8274 ± 0.0525
SMO 0.4110 ± 0.0373 0.7279 ± 0.0192
RBF Network 0.6989 ± 0.1101 0.5250 ± 0.1839
Bayesian Network 0.2754 ± 0.0224 0.9387 ± 0.0063
GBGP 0.8161 ± 0.0318 0.8963 ± 0.0412
Table 8. The comparison between GBGP to other models.
Acc. (Yes) Acc. (No)
GBGP|Logistic
Diff. 0.408 0.149
S.D. 0.054 0.045
t-stat. 7.557 3.313
GBGP|NNs
Diff. 0.504 0.069
S.D. 0.076 0.033
t-stat. 6.589 2.059
GBGP|SMO
Diff. 0.405 0.168
S.D. 0.048 0.046
t-stat. 8.448 3.669
GBGP|RBF
Diff. 0.117 0.371
S.D. 0.100 0.177
t-stat. −1.176 2.096
GBGP|Bayesian
Diff. 0.541 −0.042
S.D. 0.034 0.041
t-stat. 15.881 −1.028

H.-B. Li, M.-L. Wong
156
In addition, GBGP equipped with three competitive components. First, GBGP can generate understandable indi-
viduals for classification tasks. Second, the designed grammar can describe the problem clearly and ensure valid
individuals are generated in the learning process. The third is the token competition technique, which can im-
prove the diversity of the evolved rules in GBGP.
It would be interesting to extend the GBGP for multiple classes. For example, what types of fraudulent firms
will commit. How much do the fraudulent firms need to pay for the enforcement action? Will the fraudulent
firms commit to make fraud again? It may discover more useful information than binary classification.
Acknowledgements
The authors would like to thank Mr. LIU Si Bo for preparing the China Corporate Securities Fraud (CCSF) da-
taset. This work is partially supported by the Lingnan University Direct Grant DR13C7.
References
[1] Cumming, D.J., Hou, W.X. and Lee, E. (2011) The Role of Financial Analysts in Deterring Corporate Fraud in China.
[2] Chen, G.M., Firth, M., Gao, D.N. and Rui, O.M. (2006) Ownership Structure, Corporate Governance, and Fraud: Evi-
dence from China. Journal of Corporate Finance, 12, 424-448. http://dx.doi.org/10.1016/j.jcorpfin.2005.09.002
[3] Agrawal, A. and Chadha, S. (2005) Corporate Governance and Accounting Scandals. Journal of Law and Economics,
48, 371-406. http://dx.doi.org/10.1086/430808
[4] Wang, T.Y., Winton, A. and Yu, X.Y. (2010) Corporate Fraud and Business Conditions: Evidence from IPOs. The
Journal of Finance, 65, 2255-2292. http://dx.doi.org/10.1111/j.1540-6261.2010.01615.x
[5] Kirkos, E., Spathis, C. and Manolopoulos, Y. (2007) Data Mining Techniques for the Detection of Fraudulent Finan-
cial Statements. Expert Systems with Applications, 32, 995-1003. http://dx.doi.org/10.1016/j.eswa.2006.02.016
[6] Chen, G.M., Firth, M., Gao, D.N. and Rui, O.M. (2006) Ownership Structure, Corporate Governance, and Fraud: Evi-
dence from China. Journal of Corporate Finance, 12, 424-448. http://dx.doi.org/10.1016/j.jcorpfin.2005.09.002
[7] Chen, G.M., Firth, M., Gao, D.N. and Rui, O.M. (2005) Is China’s Securities Regulatory Agency a Toothless Tiger?
Evidence from Enforcement Actions. Journal of Accounting and Public Policy, 24, 451-488.
http://dx.doi.org/10.1016/j.jaccpubpol.2005.10.002
[8] Cox, J.D., Thomas, R.S. and Kiku, D. (2003) SEC Enforcement Heuristics: An Empirical Inquiry. Duke Law Journal,
737-779.
[9] Loveard, T. and Ciesielski, V. (2001) Representing Classification Problems in Genetic Programming. Proceedings of
the 2001 Congress on Evolutionary Computation, 2, 1070-1077.
[10] Ngan, P.S., Wong, M.L., Leung, K.S. and Cheng, J.C.Y. (1998) Using Grammar Based Genetic Programming for Data
Mining of Medical Knowledge. Genetic Programming, 254-259.
[11] Lin, J.W., Hwang, M.I. and Becker, J.D. (2003) A Fuzzy Neural Network for Assessing the Risk of Fraudulent Finan-
cial Reporting. Managerial Auditing Journal, 18, 657-665. http://dx.doi.org/10.1108/02686900310495151
[12] Wong, M.L. and Leung, K. S. (1995) Inducing Logic Programs with Genetic Algorithms: The Genetic Logic Program-
ming System. IEEE Expert, 10, 68-76. http://dx.doi.org/10.1109/64.464935
[13] Wong, M.L. and Leung, K.S. (1997) Evolutionary Program Induction Directed by Logic Grammars. Evolutionary
Computation, 5, 143-180. http://dx.doi.org/10.1162/evco.1997.5.2.143
[14] Koza, J.R. (1990) Genetic Programming: A Paradigm for Genetically Breeding Populations of Computer Programs to
Solve Problems. Department of Computer Science, Stanford University.
[15] Hopcroft, J.E. (2008) Introduction to Automata Theory, Languages, and Computation, 3/E. Pearson Education India.
[16] Goldberg, D.E. and Holland, J.H. (1988) Genetic Algorithms and Machine Learning. Machine Learning, 3, 95-99.
http://dx.doi.org/10.1023/A:1022602019183
[17] Leung, Y. and Leung, K.S. (1992) Rule Learning in Expert Systems Using Genetic Algorithms: 1, Concepts. Proceed-
ings of the 2nd International Conference on Fuzzy Logic and Neural Network, 1, 201-204.
[18] Liu, A., Ghosh, J. and Martin, C.E. (2007) Generative Oversampling for Mining Imbalanced Datasets. DMIN, 66-72.
[19] Chawla, N.V., Bowyer, K.W., Hall, L.O. and Kegelmeyer, W.P. (2002) SMOTE : Synthetic Minority Over-Sampling
Technique. Journal of Artificial Intelligence Research, 16, 321-357.