Journal of Computer and Communications, 2014, 2, 142-147
Published Online March 2014 in SciRes. http://www.scirp.org/journal/jcc
http://dx.doi.org/10.4236/jcc.2014.24019
How to cite this paper: Tongur, V. and Ülker, E. (2014) Migrating Birds Optimization for Flow Shop Sequencing Problem.
Journal of Computer and Communications, 2, 142-147. http://dx.doi.org/10.4236/jcc.2014.24019
Migrating Birds Optimization for Flow Shop
Sequencing Problem
Vahit Tongur1, Erkan Ülker2
1Computer Engineering Department, Necmettin Erbakan University, Kon ya, Tu rkey
2Computer Engineering Department, Selçuk University, Konya, Turkey
Received Novemb er 2013
Abstract
FSSP is a typical NP-Hard problem which is desired to be minimum makespan. This study consid-
ers Migrating Birds Optimization (MBO) which is metaheuristic approach for the solution of Flow
Shop Sequencing Problem (FSS P). As the basic MBO algorithm is designed for discrete problems.
The performance of basic MBO algorithm is tested via some FSSP data sets exist in literature. Ob-
tained results are compared with optimal results of related data sets.
Keywords
Migrating Birds Optimization; Flow Shop Sequencing Problem; Metaheuristic Optimization
1. Introduction
Flow shop sequencing problem (FSSP) is a production planning problem. Production planning problem in to-
day’s manufacturing systems planning process has a very important place. Therefore a lot of research has been
done on scheduling problems. Researchers have developed various heuristic approaches because of most of the
scheduling problems in NP-hard class.
There are close optimum solutions for large scaled integrated optimization problems as an optimum solution.
Close optimum solutions are generally found via heuristic algorithms. While some heuristic algorithms start to
solution from zero and represent a graded solution, some of them start from a complete solution and try to en-
hance the existing solution [1,2]. Most of the metaheuristic algorithms can also be called as neighboring or local
search procedures. Metaheuristic algorithms are a common form of enchanging algorithms which find a better
solution by looking for neighboring of existing solution in each iteration [2,3]. Neighboring attitude of each me-
taheuristic algorithm is different. It can be said that differences of these algorithms, which basically have the
same targets, are sourced from their neighboring attitudes. Until now, some metaheuristic algorithms such as
genetic algorithm [4,5], tabu search [6,7], ant colony algorithm [8] are solved by FSSP problems.
Flow shop sequencing problem minimizing the time between the beginning of perform of the first job on the
first machine and the completion of perform of the last job on the last machine. This time is called make span.
Assumptions for this problem are as follows.
• Every job has to be processed at maximum once on machine.

V. Tongur, E. Ülker
143
• Every machine processes only one job at a time.
• Every job is processed at maximum on one machine at a time.
• The preparation times of the operations are included in the processing time and do not depend on the se-
quence.
• The operating sequences of the jobs are the same on every machine [9].
FSSP can be formulated as below;
For n jobs and m machine,
Job permutation
{ }
123
,,,
n
π ππππ =
and p(i,j) processing time for job i on machine j.
()( )
11
,1 ,1Cp ππ =
(1)
( )()( )
1
,1,1,1 2,,
ii i
CCpfor in ππ π
−
=+=
(2)
( )()( )
11 1
,,1, 2,, CjCj pjforjm ππ π = −+=
(3)
()() ()
{}
( )
1
,max, ,,1,
2, ; 2,,
iii i
CjC jCjpj
for infor jm
πππ π
−
= −+
= =
(4)
Makespan
( )
max
,
n
C Cm π =
[4,5].
Organization of the article is follows; In the second section, MBO algorithm is mentioned. After telling ap-
plication of FSSP problem to MBO algorithm in third section, numeric results of MBO algorithm, which is ap-
plied to FSSP problem, is given in fourth section. In the final section, obtained results of the study are assessed.
2. Migrating Birds Optimization Algorithm
Migrating Birds Optimization algorithm (MBO) is revealed by Duman et al. [2]. They are inspired from the
flight position of migratory birds while they migrate as a flock.
Migrating Birds Optimization algorithm (MBO) is revealed as a result of studies on V formation of the birds,
which provides energy saving in flying long distances, during the migration. The reason of V formation in actual
life is commented as minimizing the necessary energy of flight by using air turbulence of leader bird’s flapping.
It is thought that birds fly in a specific angle and distance with the leader bird for using this energy saving. Wing
distances of different migrating birds, which fly in this formation, is different. As wing distances can change the
stress and position of the turbulence, the size of formation can be different for different birds (distance and angle
values between leader bird and the others) [2].
Leader bird in the flock is the one which spends the most energy. The other birds after it, take the advantage
of leader bird. When the leader bird gets tired, another bird in the flock takes its position and the tired bird goes
back side of the flock.
MBO is a neighbouring research technique including algorithm. Each bird in V formation represents a solu-
tion. Starts with first solution (leader bird) and goes on till tail. Each solution has solutions which try to advance
it. These neighboring solutions provide the opportunity of local searches in the position of existing solution. If
the neighbor solutions are better than the existing one, they are replaced. Apart from the other metaheuristic al-
gorithms, there is another efficiency mechanism in MBO algorithm. This mechanism transfers the best unused
neighbor solutions to following solution. In algorithm, this situation is called as sharing the neighbors. In this
way, existing solution enhances itself by using not only its own produced solutions but also neighbor solutions
which come from other solutions. This neighbor sharing is concluded with sharing of the solution by all birds
(except for the last two birds in the tail). After that the leader bird is changed and new neighborhoods and
neighbor sharing, which will be produced by new leader bird, is restarted. This process continues until deter-
mined iteration value is reached [2].
Pseudo code of MBO algorithm is given below;

V. Tongur, E. Ülker
144
n: amount of beginning solutions (number of birds)
k: number of related neighbour solutions
x: number of neighbour solutions which are shared by final
m: number of lap
K: iteration limit [2]
Algorithm shows similarities with real life of migrating birds. n value shows number of birds. First birds are
in V formation. An existing solution is produced for each bird. k value is thought as speed of a bird in real life.
The bird should fly slowly for a more detailed discovery around itself. So k parameter is expected to have low
values in order to be able to reach better solutions. x value is thought as wing distance of the bird (WTS length
in Fig ur e 1). In experimental studies of Lissaman and Schollenberger, optimum wing distance for the 1.5 meter
wing length birds is determined as 16 cm [2,10]. Which means that x parameter will be appointed very low val-
ues. m value is thought as number of flutter of the bird. It is the flutter number until leader bird gets tired and
goes back for resting. According to algorithm, when leader bird gets tired it goes to the back of flock and its
following bird becomes leader bird. As the birds are in V formation, first the bird on the left of the leader bird
takes the position of leader bird. In this condition leader bird goes to the back line of the left order. In the next
change, the bird on the right of the leader bird takes its position and leader goes to the right back of the flock.
And the iteration number of algorithm should be as much as that each bird would become leader at least once
[2].
3. Solution of FSSP with MBO Algorithm
Basic MBO algorithm is tested on quadratic assignment problems (QAP) [11]. Its structure resembles to genetic
algorithm partially. While solving QAP problems, it is incorporated into problem permutation line as in genetic
algorithm. While determining neighbor solutions, only one pair of existing solution is replaced. So, producing
neighborhood is thought to enable a more detailed local search.
MBO algorithm also has a similar structure of chromosome which is used in genetic algorithm. As discrete
problems such as QAP are designed, basic MBO algorithm is kept the same for FSSP. Also enhanced parame-
ters are used which are obtained via QAP samples.
As in most metaheuristic algorithms, MBO starts with a beginning solution. In the beginning, permutation of
all jobs on all machines is created for each bird and make span is determined. For n job and m machine m × n
matrix is formed. Therefore all jobs and all machines are placed in the m × n matrix. After that neighboring is
produced for each bird in the flock in enough amounts and if the best neighbor of the existing solution is better
1. Generate n initial solutions in a random manner and place them on an hypothetical V
formation arbitrarily
2. i = 0
3. while(i< K)
4. for (j = 0; j < m; j++)
5. Try to improve the leading solution by generating and evaluating k neighbors of it
6. i = i + k
7. for each solution sr in the flock (except leader)
8. Try to improve sr by evaluating (k–x) neighbors of it and x unused best neighbors
from the solution in the front
9. i = i +
(k - x)
10. endfor
11. endfor
12. Move the leader solution to the end and forward one of the solutions following it to the
leader position
13. endwhile
14. return the best solution in the flock
n: amount of beginning solutions (number of birds)
k: number of related neighbour solutions
x: number of neighbour solutions which are shared by final solution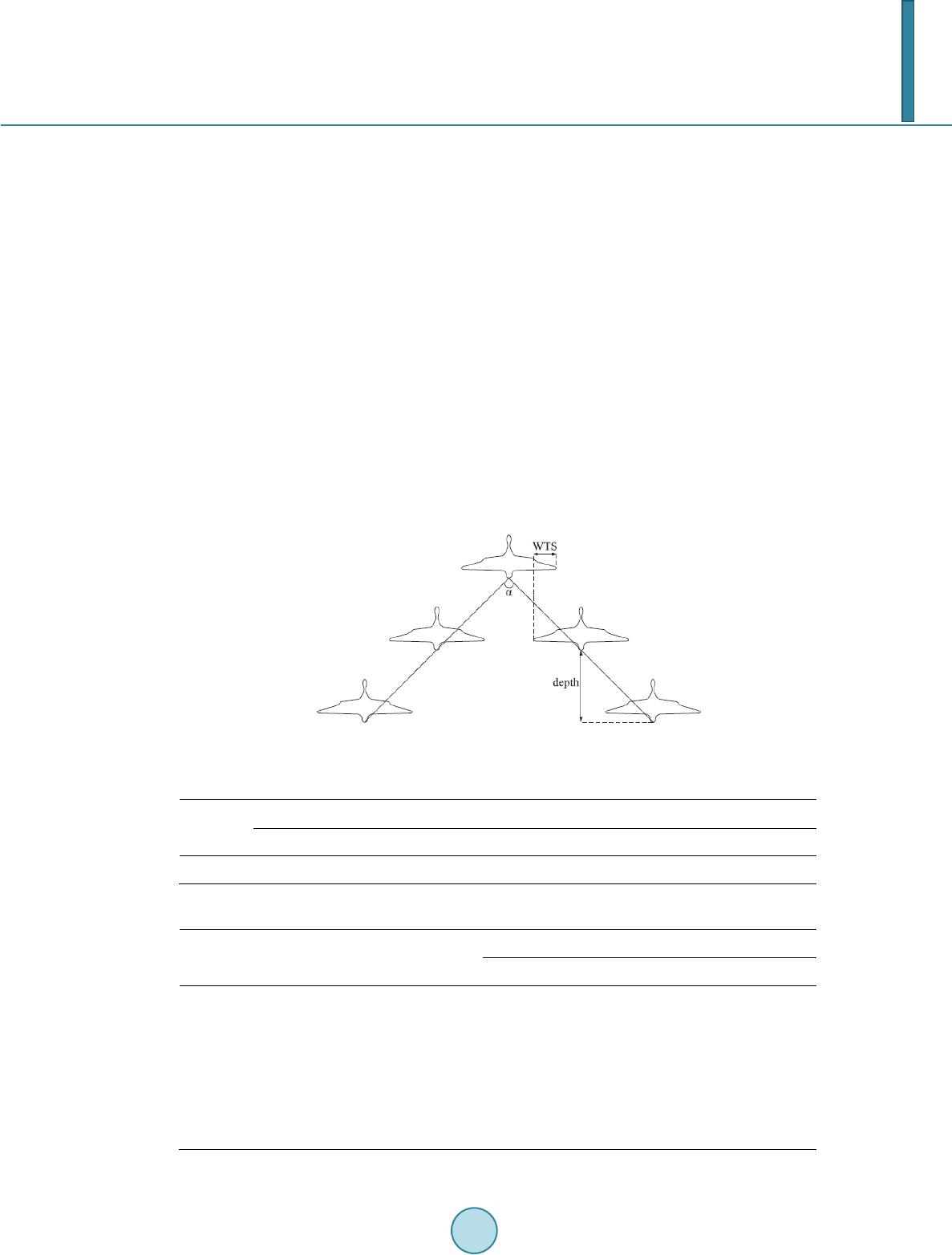

V. Tongur, E. Ülker
145
than the existing solution, neighbor solution is replaced by existing solution. Neighbors are produced faithfully
to original algorithm. The best unused solution is transferred to the bird in the back order. And the worst unused
solution of the related bird’s back order is dismissed.
4. Experimental Res ult s
In the application, MBO algorithm is tested Taillard’s flow shop sequence problems [12]. All tested problems
are executed 10 times by keeping the starting point same and results are averaged. Iteration value of basic MBO
algorithm is depended upon the produced neighbor amount and size of the problem. This value determined as n4
(n = job count). In both problems, static parameter values are given in Table 1.
Values for 10 times execution of all tested problems are saved. According to these values, maxi mum,
minimum and average values of makespan are given in Tables 2-4 which are calculated by considering average
of 10 studies for some iteration.
Best known upper bounds of tested Taillard’s instances are given in Table 5.
5. Conclusion
In this article, solutions are seeked for the well known optimization problem flow shop sequencing problem with
migrating birds optimization (MBO) algorithm which is a new metaheuristic approach. Developed algorithm is
experimentally tested by well known data set which are chosen fro m Taillard’s benchmark and compared
Figure 1. The V formation.
Table 1. Starting parameter values.
MBO Parameters
n k x m
51 3 1 10
Table 2. Maximum, minimum and average values for 20 × 5 instance1.
Leader Replace Number 20 × 5 instance1
Min. Max. Avg.
1 1334.4 1426 1374.5
5 1297 1340.5 1311.6
10 1295.7 1305.9 1297.9
50 1291.2 1297 1295.4
100 1288.1 1296.8 1291.3
156 1284.5 1290.1 1287.9

V. Tongur, E. Ülker
146
Table 3. Maximum, minimum and average values for 20 × 10 instance1.
Leader Replace Number 20 × 10 instance1
Min. Max. Avg.
1 1755.6 1890.4 1825
5 1658.8 1758.3 1711.1
10 1639.8 1712.6 1676.3
50 1601.9 1646.3 1624.7
100 1594.2 1635 1615.3
156 1591 1627.2 1610.6
Table 4. Maximum, minimum and average values for 20 × 20 instance1.
Leader Replace Number 20 × 20 instance1
Min. Max. Avg.
1 2474.9 2629.6 2552.4
5 2395.4 2497.7 2448.7
10 2364.2 2455.1 2413.5
50 2325.6 2392.6 2355.4
100 2320.6 2375.3 2343
156 2318.9 2362.9 2337.7
Table 5. Upper bound values of tested problems.
Upper Bound Values
20 × 5 ins.1 20 × 10 ins.1 20 × 20 ins.1
1278 1582 2297
according to opti ma l solutions. As a result of proposed study , forFSSP; it is seen that MBO algorithm follows a
performance progress and has a more consistent appr oach to result.
Acknowledgements
This study has been supported by Scientific Research Project of Necmettin Erbakan University.
References
[1] Glover, F. and Kochenberger, G.A. (2003) Handbook of Metaheuristics. Kluwer Academic Publishers.
[2] Duman, E., Uy sal , M. and Alkay a, A. F. (2012) Migrating Birds Optimization: A New Metaheuristic Approach and Its
Performance on Quadratic Assignment Problem. Information Sciences, 217, 65-77.
http://dx.doi.org/10.1016/j.ins.2012.06.032
[3] Ahuja, R.K., Ergun, O. , Orlin, J.B. and Punnen, A.P. (2002) A Survey of Very Large Scale Neighborhood Search
Techniques. Discrete Applied Mathematics, 123, 75-102. http://dx.doi.org/10.1016/j.ins.2012.06.032
[4] Reeves, C.R. (1995) A Genetic Algorithm for Flowshop Sequencing. Computers & Operations Research, 22, 5-13 .
http://dx.doi.org/10.1016/0305-0548(93)E0014-K
[5] Reeves, C.R. and Yamada, T. (1998) Genetic Algorithms, Path Relinking and the Flowshop Sequencing Problem. Evo-
lutionary Computation Journal (MIT Press), 6, 230-234.

V. Tongur, E. Ülker
147
[6] Armentano, V.A. and Ronconi, D.P. (1999) Tabu Search for Total Tardiness Minimization in Flowshop Scheduling
Problems. Computers & Operations Research, 26, 219-235.
[7] Ekşioğlu, B., Ekşioğlu, S.D. and Ja in, P. (1998) A Tabu Search Algorithm for the Flowshop Scheduling Problem with
Changing Neighborhoods. Computer & Industrial Engineering, 1-11.
[8] Rajendran, C. a nd Ziegler, H. (2004) Ant -Colony Algorithms for Permutation Flowshop Scheduling to Minimize Ma-
kespan/Total Flowtime of Jobs. European Journal of Operational Research, 155, 426-438.
[9] Taillard, E. (1989) Some Efficient Heuristic Methods for the Flow Shop Sequencing Problem.
[10] Lissaman, P.B.S. and Shollenberger, C.A. (1970) Formation Flight of Birds. Science, 168, 1003-1005.
http://dx.doi.org/10.1126/science.168.3934.1003
[11] Burkard, R.E. , Çel a, E., Karisch, S.E. and Rendl, F. (2010) QAPLIB Aquadratic Assignment Problem Library.
http://www.opt.math.tu-graz.ac.at/qaplib/
[12] Taillard, E. (2013) Scheduling Instances.
http://mistic.heig-vd.ch/taillard/problemes.dir/ordonnancement.dir/ordonnancement.html