 Journal of Computer and Communications, 2014, 2, 127-136 Published Online March 2014 in SciRes. http://www.scirp.org/journal/jcc http://dx.doi.org/10.4236/jcc.2014.24017 How to cite this paper: Kiran, M.S. and Gündüz, M. (2014) The Analysis of Peculiar Control Parameters of Artificial Bee Co- lony Algorithm on the Numerical Optimization Problems. Journal of Computer and Communications, 2, 127-136. http://dx.doi.org/10.4236/jcc.2014.24017 The Analysis of Peculiar Control Parameters of Artificial Bee Colony Algorithm on the Numerical Optimization Problems Mustafa Servet Kiran, Mesut Gündüz Computer Engineering Department, Selçuk University, Kony a, Turk ey Email: mskiran@selcuk .edu.tr, mgunduz@selcuk.edu.tr Received Novemb er 2013 Abstract Artificial bee colony (ABC) algorithm is one of the popular swarm intelligence algorithms. ABC has been developed by being inspired foraging and waggle dance behaviors of real bee colonies in 2005. Since its invention in 2005, many ABC models have been proposed in order to solve differ- ent optimization problems. In all the models proposed, there are only one scout bee and a con- stant limit value used as control parameters for the bee population. In this study, the performance of ABC algorithm on the numeric optimization problems was analyzed by using different number of scout bees and limit values. Experimental results show that the results obtained by using more than one scout bee and different limit values, are better than the results of basic ABC. Therefore, the control parameters of the basic ABC should be tuned according to given class of optimization problems. In this paper, we propose reasonable value ranges of control parameters for the basic ABC in order to obtain better results on the numeric optimization problems. Keywords Artificial Bee Colony; Effects of the Parameters Parameter Tuning; Number of Scout Bee; Limit Value 1. Introduction Artificial Bee Colony algorithm was developed by Karaboga in 2005, inspired intelligent behaviors of real ho- ney bee colonies [1]. The ABC simulates foraging and dance behaviors of real bees to achieve global optimum for different optimization problems. Although the foraging behavior of real bees is to collect nectar from food sources around the hive in nature, artificial foraging in ABC is to search the solution space and to evaluate solu- tion parameters found [1]. In the ABC, the dance of the bees in the hive is used in order to share information about the positions of food sources between onlooker and employed bees as well as in nature [1,2]. The other type of bee is scout bee that works for foraging. A scout bee searches around the hive for finding new food sources. If an employed bee could not improve the self solution in a certain time, it becomes scout bee the main purpose of which is to increase search ability of the  M. S. Kiran, M. Gündüz ABC. In addition, scout bees provide to get rid of local minimums by preventing stagnation of the bee popula- tion. In this point, th e number of scout bees and when a scout bee occurs from employed bees are important fac- tor for the ABC. When the number of scout bees is a very large value and time of occurrence of scout bee (called as limit) is short, exploitation from food source ability of ABC decreased. When the number of scout bees is a very small value and time of occurrence of scout bee is long, probability of getting rid of local mini- mum of the ABC decreased. Therefore, the number of scout bees and the time of occurrence of scout bee should be balanced for the problems. The performance of ABC algorithm is partially analyzed under the different limit values in [3,4], but the other peculiar parameter (number of scout bees) of ABC algorithm is taken as 1. In this study, we reported that ABC has two peculiar control parameters and tested effect of control parameters to the performance of ABC for nu- meric optimization problems. The paper is organized as follows; Section 1 presents introduction and literature review, The ABC algorithm is given in Section 2, experiments are presented in Section 3. The simulation results obtained are discussed in Section 4 and finally, conclusion and future works are given in Section 5. Literature Review The ABC algorithm was first introduced by Karaboga in 2005 and applied to well-known three numerical func- tions for finding global minimum [1]. Performance of ABC algorithm was compared with genetic algorithm (GA), particle swarm optimization (PSO) and differential evolution (DE) on the multivariable numerical opti- mization problems [3-5] and Karaboga [6] used a new method based on ABC algorithm for designing digital in- finite impulse response (IIR) filters and its performance was compared to other techniques. Performance of ABC was examined on large set numerical optimization problems and compared with GA, PSO, DE and evolution strategies in [7]. In order to improve ABC algorithm, many researchers proposed new approaches such as [8-12]. Besides improvements of ABC, ABC was used for solving many optimization problems such as [13-23]. As seen above the literature review, the basic ABC algorithm has many modifications and applications but the peculiar control parameters of the ABC algorithm have not been analyzed yet. In this paper, we analyzed the peculiar control parameters of the ABC algorithm by the different limit values, number of scout bees and popu- lation size. 2. The ABC Algorithm The basic ABC algorithm has very simple, clear and adaptable model. There are two kinds of foragers in the hive of ABC, employed foragers and unemployed foragers. Employed foragers exploit from food sources (cor- responded to the potential solution of the optimization problem) continuously and they carry information about positions of food sources to the hive. There are two types of unemployed foragers, onlooker bees and scout bees. The onlooker bees go to food source in order to exploit by taking advantage of information shared by employed foragers. The scout bees search new food source around the hive and mean of number of scout bees averaged over conditions is about 5% - 10% [1,24]. In the nature, although 5% - 10% of the population is scout bee, there is only one scout bee in the ABC hive. Also, in the basic ABC, half of the population is employed bees and other half of the population is onlooker bees. After tasks of the bees were explained, these tasks are performed as follows: the employed bees use the Equa- tion (1) in order to improve self solution (let vi = xi). {}{ } ,, ,, 1, 2,,,and1, ) 2, ( ijijij kj vx x D x jki kn∈ ≠∈ = +Φ− (1) where, is ith employed bee, is the candidate solution for , is a neighbor employed bee of , is a number randomly selected in the range [−1, 1], n is number of the employed bees, D is the dimensional- ity of the problem and and are selected randomly. In addition, only one para- meter of the employed bee is updated at the each iteration. Therefore, all solution parameters of the employed bee are copied to the candidate solution produced this bee for evaluating objective function. If an employed bee could not improve self solution in a certain time (during the achieving the limit), it be-  M. S. Kiran, M. Gündüz comes a scout bee and a new solution is generated for it by using the following equation: minmax min () jjj j i x xrxx= +×− , for all (2) where, is a parameter to be optimized for the ith employed bee on the dimension j of the D-dimensional so- lution space , and are the upper and lower bounds for , respectively and r is a random number in range of [0, 1]. After the generating a new solution, the scout bee becomes the employed bee. Every onlooker bee memorizes the solution of one of n employed bees based on fitness values of the em- ployed bees in order to generate a new food position by using Equation (1). Onlooker bees select an employed bee by using roulette wheel selection mechanism and the Equation (3): pi is to be selected probability of the ith employed bees and calculated as follows: (3) where, is the fitness value of ith employed bee and is computed as follows: 1( 0) 1 1( )(0) i i i ii if f f fit abs fiff ≥ + = +< (4) where, fi is the object function value which is specific for the problem. Also, initial solutions for the employed bees are produced by using the Equation (2) in initialization of the ABC algorithm. As seen from the Figure 1, in order to exploit from food sources, the onlooker bees and employed bees use the same equation. For the initial solutions for employed bees and generating new solution for scout bee, the Equation (2) is used. 3. Experiments In order to analyze effects of number of scout bees and limit parameters to performance, the experiments were designed on the well-known five numerical functions. The design parameters are number of scout bees, limit values and size of the population. Size of the population opts as 20, 50 and 100. Number of scout bees is from 1 up to number of employed bees. The limit values depend on dimensionality of the problem and number of employed bees. According to [1,7], limit value of the population is calculated as follows; (5) where is the parameter which is control occurrence of the scout bee, is number of employed bees and is dimensionality of the optimization problem. The limit value obtained from the Equation (5), is used as maximum limit value in the experiments. Also, limit values used in experiments are calculated as follows: ( 1,2,...,5) 5 i Limit Li i =×= (6) where, L is the limit value used in experiments, L imit is obtained from the Equation (5) and i is used for deter- mining limit value. Also, all the parameters are shown in Table 1. In all experiments, dimensionality of the numerical functions is taken as 50 and maximum evaluation number (MEN) which is used as stopping criterion, is calculated as follows [25]: ( 7) where D is the dimensionality of the numerical function. Each of the experiments was repeated 30 times with random seeds for each limit value and number of scout bees, and mean of the value obtained by the runs was shown in the figures.  M. S. Kiran, M. Gündüz Table 1. Control parameters used in the experiments. Population Size Maximum Limit Number of Scout Bees Experiment 1 20 500 From 1 to N* Experiment 2 50 1250 From 1 to N* Experiment 3 100 2500 From 1 to N* *N is the number of employed bees. The numerical functions used in the experiments have some characteristic features. If a function has more than one local optimum, this function is named “multimodal”. Unimod al functions have only one local optimum and this local optimum is the global minimum. If an-variable function can be written as the sum of n functions of one variable, this function is called “separable”, otherwise the function is non-separable. Non-separable func- tions have interrelation among their variables. Also, the dimensionality of the search space is important issue with the problem [7,26]. By using these functions in the experiments, search and getting rid of local minimum abilities of the ABC algorithm under the different conditions (different number of scout bees and limit values) are investigated. 3.1. The Sphere Function The Sphere which is proposed by De Jong [27] in order to evaluate the capabilities of different adaptive strate- gies has one local minimum and this local minimum is global minimum which is on point and the global minimum value is 0. The function is formulated as follows: 2 1 ( )([ 100,100]) DD i i fx xx = = ∈− ∑ (8) Because the Sphere function is separable, unimodal, simplicity and symmetry, it is easy to solve with respect to other numerical functions for optimization algorithms. The obtained results are shown in Figure 1 while pop- ulation size is 20, 50 and 100. 3.2. The Rastrigin Function The Rastrigin function [28] is multimodal and separable. The search domain of the function is in range [−5.12, 5.12]. In this range, global minimum of the Rastrigin function is on and on this point, . Its contour is made up of a large number of local minima whose value increases with the distance to the global minimum. The function is described as follows: 2 1 ( )[10cos(2)10] D ii i fx xx π = =−+ ∑ (9) The obtained results by ABC algorithm with control parameters are given in Figure 2. 3.3. The Griewank Function The Griewank function [29] is non-separable and multimodal features. Number of local minimum is huge. The global minimum is on and this point, . Search domain is range of [−600, 600]. The Griewank function is defined as follows: 2 11 1 ( )cos1 4000 D Di i ii x fx xi == =−+ ∑∏ (10) Figure 3 shows the obtained results by ABC algorithms under the different values of control parameters. 3.4. The Ackley Function The Ackley function, originally proposed by Ackley [30] and generalized by Bäck and Schwefel [31], is 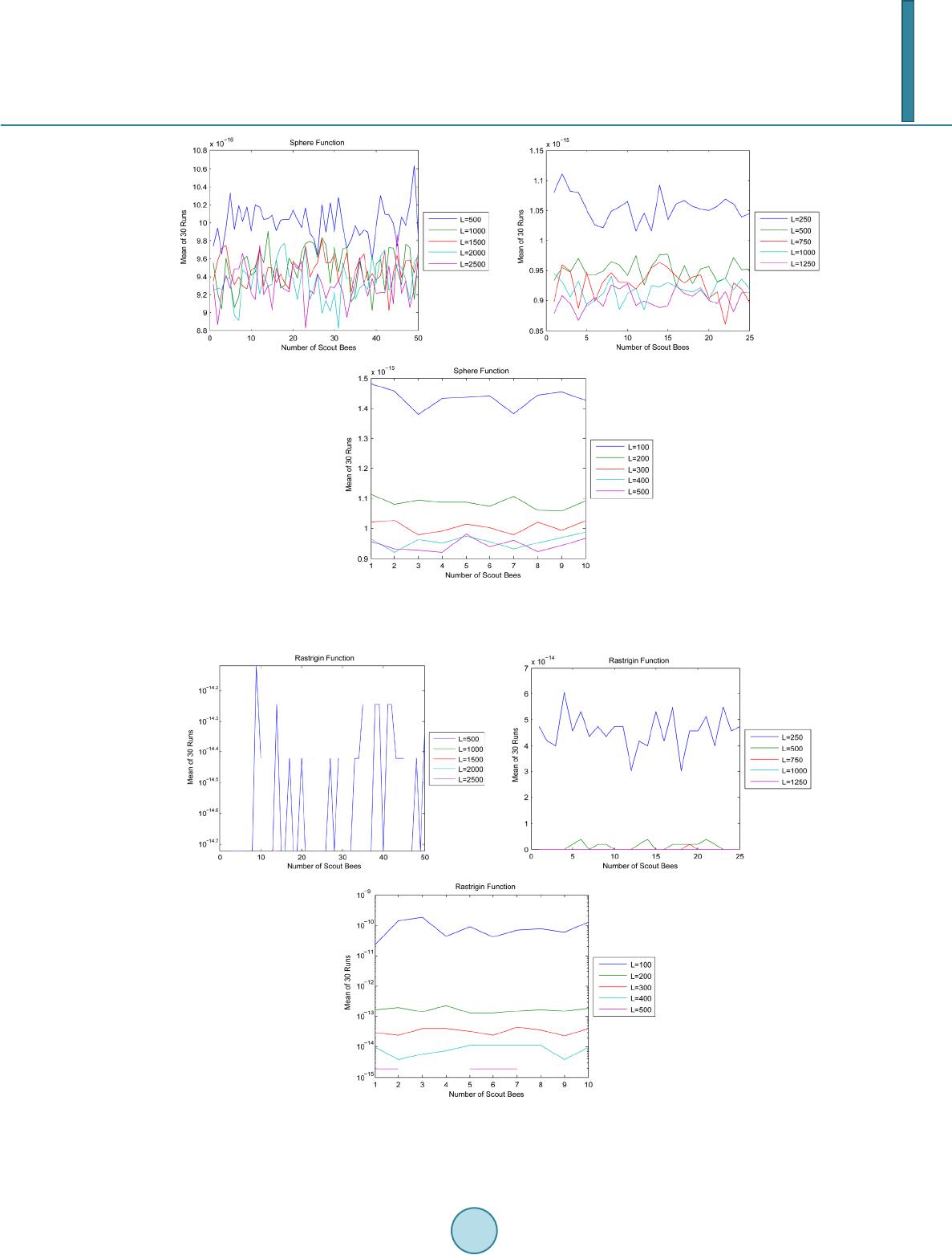 M. S. Kiran, M. Gündüz (a) (b) (c) Figure 1. The means of 30 runs for the Sphere function. (a) Population size = 100; (b) Population siz e = 50; (c) Population size = 20. (a) (b) (c) Figure 2. The means of 30 runs for the Rastrigin function. (a) Population size = 100; (b) Population siz e = 50; (c) Population size = 20.  M. S. Kiran, M. Gündüz (a) (b) (c) Figure 3. The means of 30 runs for the Griewank function. (a) Population si ze = 100 ; (b) population size = 50; (c) Population size = 20. multimodal and non-separ able, and has an exponential term that covers its surface with numerous local minima. The global minimum value is 0 and the global minimum is located in the origin. Search domain of the function is in range [−32, 32] and its formulation is given in Equation (11): 2 11 11 ( )20exp0.2expcos(2)20 DD ii ii fxxx e DD π = = =− −−++ ∑∑ (11) For Ackley function, ABC with different values of control parameters is applied and obtained results show in Figure 4. 3.5. The Rosenbrock Function The Rosenbrock’s banana function, first proposed by Rosenbrock [32], is non-separable because of interrelation between variables. It is unimodal for D = 2 and D = 3 but may have multiple minima in high dimension cases and its global minimum is inside a narrow, curved valley [33]. Due to the non-linearity of the valley, many algo- rithms converge slowly because they change the direction of the search repeatedly [26]. Global minimum is on and this point . Search domain of the Rosenbrock function is in the range [−30, 30] and it is denoted as follows: ( ) ( ) 122 2 1 1 ( )1001 D ii i i fxx xx − + = =− +− ∑ (12) The results obtained by ABC algorithm for Rosenbrock function is given in Figure 5.  M. S. Kiran, M. Gündüz (a) (b) (c) Figure 4. The means of 30 runs for the Ackley function. (a) Population size = 100; (b) Population size = 50; (c) Population size = 20. (a) (b) (c) Figure 5. The means of 30 runs for Rosenbrock function. (a) Population size = 100; (b) Population size = 50; (c) Population size = 20.  M. S. Kiran, M. Gündüz 4. Result and Discussion As seen from figures belonged to the experiments, when the population size is increased, effects of scout bee and limit values decrease because great population size provides enough diversity in the population for the problem. For all functions, when population size is taken as 100, the ABC algorithm shows high performance but in this case, effects of peculiar control parameters are not seen. When population size is taken as 50, perfor- mance of ABC algorithm is slightly reduced and the smallest limit value in the experiments prevents from reaching saturation of the population. Effects of number of scout bees are clearly seen when population size is taken as 20. While population size is 20, for all functions except Rosenbrock function, when number of scout bees is taken as 15% - 30% of the population, the good results are obtained with respect to others. For the Rosenbrock function, because it has peculiar features (global minimum is inside a narrow, curved valley), the search ability of the ABC algorithm which is provided by scout bees and limit value, is the most important factor for finding the global minimum. As seen from the Figure 5, the search ability and performance of ABC algorithm increases, when the number of scout bees is chosen a greater number than one and the limit value is chosen a little number with respect to others. The actual effect of number of scout bees and limit value is to provide to prevent from stagnation of the pop- ulation. Stagnation of the population is to come together on the same point all of the individuals and not to pro- duce a new solution interaction between them. Therefore, more than one scout bee and limit value ease to get rid of local optimum of the population and many scout bees and small limit value provide to increase search ability of the ABC algorithm. The good search ability ensures to find minimum points on the solution space. After ana- lyzing the number of scout bees and limit values, we propose that number of scout bees can be 10% - 30% of the population and limit value can be selected nearby of value obtained by equation 13 for this class of optimization problems. (13) Where D is the dimensionality of the optimization problem and N is the number of employed or onlooker bees. Finally, the search and exploitation abilities in the ABC algorithm should be balanced using limit, number of scout bees and population size in order to obtain better quality results in a reasonable time. 5. Conclusion and Future Works This work examined performance of ABC algorithm with the different control parameters on the well-known five numerical benchmark functions. From the results obtained in this work, peculiar control parameters (num- ber of scout bees and limit value) of the ABC algorithms should be tuned in order to obtain better results for the multimodal and multidimensional optimization problems. Future works include adaptive approaches for number of scout bees and limit value for the population. Acknowledgements This study has been supported by the Selcuk University Scientific Projects Coordinatorship. References [1] Karaboga, D. (2005) An Idea Based on Honey Bee Swarm for Numerical Optimization. Technical Report-TR06, Er- ciyes University. http://mf.erciyes.edu.tr/abc/pub/tr06_2005.pdf [2] Frisch, K.V. (1992) Decoding Language of the Bee. Nobel Lectures. In: Lindsten, J., Ed., Physiology or Medicine 1971-1980, World Scientific Publishing, Singapore. [3] Karaboga, D. and Basturk, B. (2008) On the Performance of Artificial Bee Colony (ABC) Algorithm. Applied Soft Computing, 8, 687-697. http://dx.doi.org/10.1016/j.asoc.2007.05.007 [4] Akay, B. (2009) Performance Analysis of Artificial Bee Colony Algorithm on Numerical Optimization Problems. Ph.D. Thesis, Erciyes University, Graduate School of Natural and Applied Sciences, Kayseri, 70-72. [5] Karaboga, D. a nd Basturk, B. (2007) A Powerful and Efficient Algorithm for Numerical Function Optimization: Ar- tificial Bee Colony (ABC) Algorithm. Journal of Global Optimization, 39, 459-471.  M. S. Kiran, M. Gündüz http://dx.doi.org/10.1007/s10898-007-9149-x [6] Karaboga, N. (2009) A New Design Method Based on Artificial Bee Colony Algorithm for Digital IIR Filters. Journal of The Franklin Institute, 346, 328-348. http://dx.doi.org/10.1016/j.jfranklin.2008.11.003 [7] Karaboga, D. and Akay, B. (2009) A Comparative Study of Artificial Bee Colony Algorithm. Applied Mathematics and Computation, 214, 108-132. http://dx.doi.org/10.1016/j.jfranklin.2008.11.003 [8] Tsai, P. -W., Pan, J.-S. , Liao, B.-Y. and Chu, S. -C. (2009) Enhanced Artificial Bee Colony Optimization. International Journal of Innovative Computing, 5, 5081-5092. [9] Singh, A. (2009) An Artificial Bee Colony Algorithm for the Leaf Constrained Minimum Spanning Tree Problem. Ap- plied Soft Computing, 9, 625-631. http://dx.doi.org/10.1016/j.asoc.2008.09.001 [10] Alatas, B. (2010) Chaotic Bee Colony Algorithms for Global Numerical Optimization. Expert Systems with Applica- tions, 37, 5682-5687. http://dx.doi.org/10.1016/j.eswa.2010.02.042 [11] Zhu, G. and Kwong, S. (2010) Gbest-Guided Artificial Bee Colony Algorithm for Numerical Function Optimization. Applied Mathematics and Computation, 217, 3166-3173. http://dx.doi.org/10.1016/j.amc.2010.08.049 [12] Akay, B. and Karaboga, D. (2010) A Modified Artificial Bee Colony Algorithm for Real Parameter Optimization. In- formation Sciences. http://dx.doi.org/10.1016/j.ins.2010.07.015 [13] Zhang, C., Ouyang, D. and Ning, J. (2010) An Artificial Bee Colony Approach for Clustering. Expert Systems with Applications, 37, 4761-4767. http://dx.doi.org/10.1016/j.eswa.2009.11.003 [14] Tasgetiren, M.F., Pan, Q.-K., Suganthan, P.N. and Chen, A.H-.L. (2011) A Discrete Artificial Bee Colony Algorithm for the Total Flowtime Minimization in Permutation Flow Shops. Information Sciences, 181, 3459-3475. http://dx.doi.org/10.1016/j.ins.2011.04.018 [15] Horng, M-.H. (2011) Multilevel Thresholding Selection Based on the Artificial Bee Colony Algorithm for Image Seg- mentation. Expert Systems with Applications. http://dx.doi.org/10.1016/j.eswa.2011.04.180 [16] Ma, M., Liea ng, J., Guo, M., Fan , Y. and Yin, Y. (2011) SAR Image Segmentation Based on Artificial Bee Colony Algorithm. Applied Soft Computing. http://dx.doi.org/10.1016/j.asoc.2011.05.039 [17] Manoj, V.J. and Elias, E. (2011) Artificial Bee Colony Algorithm for the Design of Multiplier-Less Nonuniform Filter Bank Transmultiplexer. Information Sciences. http://dx.doi.org/10.1016/j.ins.2011.02.023 [18] De Oliveira, I.M.S. and Schirru, R. (2011) Swarm Intelligence of Artificial Bees Applied to In-Core Fuel Management Optimization. Annals of Nuclear Energy, 38, 1039-1045. http://dx.doi.org/10.1016/j.anucene.2011.01.009 [19] Samanta, S. and Chakraborty, S. (2011) Parametric Optimization of Some Non-Traditional Machining Processes Using Artificial Bee Colony Algorithm. Engineering Applications of Artificial Intelligence. http://dx.doi.org/10.1016/j.engappai.2011.03.009 [20] Yeh, W.-C. and Hsi eh, T.-J. (2011) Solving Reliability Redundancy Allocation Problems Using an Artificial Bee Co- lony Algorithm. Computers & Operations Research, 38, 1465-1473. http://dx.doi.org/10.1016/j.cor.2010.10.028 [21] Sonmez, M. (2011) Artificial Bee Colony Algorithm for Optimization of Truss Structures. Applied Soft Computing, 11, 2406-2418. http://dx.doi.org/10.1016/j.asoc.2010.09.003 [22] Gozde, H. and Taplamacioglu, M.C. (2011) Comparative Performance Analysis of Artificial Bee Colony Algorithms for Automatic Voltage Regulator (AVR) Syste ms . Journal of The Franklin Institute. http://dx.doi.org/10.1016/j.jfranklin.2011.05.012 [23] Szeto, W.Y., Wu, Y. and Ho, S.C. (.2011) An Artificial Bee Colony Algorithm for the Capacitated Vehicle Routing Problem. European Journal of Operational Research. http://dx.doi.org/10.1016/j.ejor.2011.06.006 [24] Seeley, T.D. (1995) The Wisdom of the Hive. Harvard University Press, Cambridge. [25] Suganthan, P.N., Hansen, N. , Liang, J.J., Deb, K., Chen, Y. -P., Auger, A. and Tiwa ri, S. (2005) Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real Parameter Optimization. Technical Report, Nanyang Technological University, Singapore. [26] Boye r, D.O., Martinez, C. H. and Pedrajas, N.G. (2005) Crossover Operator for Evolutionary Algorithms Based on Population Features. Journal of Artificial Intelligence Research, 24, 1-48. http://dx.doi.org/10.1007/s10462-005-3854-y [27] De Jong, D. (1975) An Analysis of the Behavior of a Class of Genetic Adaptive Systems. Ph.D. Thesis, Department of Computer and Communication Sciences, University of Michigan, Ann Arbor. [28] Rastrigin, L.A. (1974) Extremal Control Systems. In Theoretical Foundations of Engineering Cybernetics Series, Mos- cow. [29] Griewank, A.O. (1981) Generalized Descent for Global Optimization. Journal of Optimization Theory and Applica- tions, 34, 11-39. http://dx.doi.org/10.1007/BF00933356  M. S. Kiran, M. Gündüz [30] Ackley , D.H. (1987) An Empirical Study of Bit Vector Function Optimization. In: Davis, L., Ed., Genetic Algorithms and Simulated Annealing, Morgan Kaufmann, Los Altos, 171-204. [31] Bäck, T. and Schwefel, H.P. (1993) An Overview of Evolutionary Algorithms for Parameter Optimization. Evolution Computing, 1, 1-23. http://dx.doi.org/10.1162/evco.1993.1.1.1 [32] Rosenbrock, H.H. (1960) An Automatic Method for Finding the Greatest or Least Value of a Function. Computer Journal, 3, 175-184. http://dx.doi.org/10.1093/comjnl/3.3.175 [33] Shang, Y.W. a nd Qiu, Y.H. (2006) A Note on the Extended Rosenbrock Function. Evolution Computing, 14, 119-126. http://dx.doi.org/10.1162/evco.2006.14.1.119
|