 Journal of Computer and Communications, 2014, 2, 117-126 Published Online March 2014 in SciRes. http://www.scirp.org/journal/jcc http://dx.doi.org/10.4236/jcc.2014.24016 How to cite this paper: Findik, O., Kiran, M.S. and Babaoğlu, I. (2014) Investigation Effects of Selection Mechanisms for Gravitational Search Algorithm. Journal of Computer and Communications, 2, 117-126. http://dx.doi.org/10.4236/jcc.2014.24016 Investigation Effects of Selection Mechanisms for Gravitational Search Algorithm Oğuz Findik1, Mustafa Servet Kiran2, Ismail Babaoğlu2 1Computer Engineering Department, Abant Izzet Baysal University, Bolu, Turkey 2Computer Engineering Department, Selçuk University, Konya, Turkey Email: oguzf@ibu.edu.tr, mskiran@selcuk.edu.tr, ibabaoglu@selcu k.edu.tr Received Novemb er 2013 Abstract The gravitational search algorithm (GSA) is a population-based heuristic optimization technique and has been proposed for solving continuous optimization problems. The GSA tries to obtain op- timum or near optimum solution for the optimization problems by using interaction in all agents or masses in the population. This paper proposes and analyzes fitness-based proportional (rou- lette-wheel), tournament, rank-based and random selection mechanisms for choosing agents which they act masses in the GSA. The proposed methods are applied to solve 23 numerical benchmark functions, and obtained results are compared with the basic GSA algorithm. Experi- mental results show that the proposed methods are better than the basic GSA in terms of solution quality. Keywords Gravitational Search Algorithm; Roulette-Wheel Selection; Tournament Selection; Rank-Based Selection; Random Selection; Continuous Optimization 1. Introduction Optimization process in computer science is to find the best solution from all feasible solutions, in which the best solution maximizes the profit function or minimizes the cost function. Especially if optimization problems have high dimensions or non-linear characteristics, to find optimal solution is so hard because search space of optimization problem increases exponentially with dimension increasing. To overcome this situation, many optimization algo- rithms especially inspired from nature have been suggested in recent years such as particle swarm optimization de- veloped by inspiring bird flocking or fish schooling [1], ant colony algorithm which simulates behavior of real ants between nest and food source [2], bee colony algorithms which were inspired intelligent behavior of honey bees [3,4]. In addition to these algorithms, some algorithms which were inspired by various natural events were devel- oped. Such as harmony search algorithm inspired by natural musical performance process when a musician seek for a better condition of harmony [5], genetic algorithm based on natural evolution [6] and the GSA simulated Newton’s law of gravity [7]. The GSA is a heuristic optimization technique which is inspired by Newton’s law of gravity [7]. In this algorithm, the main rule is that each agent has features attract masses to extend each other. When all agents attract each other,  O. Findik et al. the effect which agents have big masses to solution is decrease, so to find optimum solution is difficult and the con- vergence of the method to the optimum or near optimum has slowed. Which masses will be attraction effect and which masses will be disregard is a problem in the GSA. To overcome this problem, selection mechanisms in the GSA are analyzed in this study. The rest of paper is organized as follows: Section 2 presents a literature review for the GSA. The basic GSA and the selection mechanism are explained in Section 3. The experiments are presented in Section 4. Section 5 discusses the experimental results and the study and finally, conclusion and future works are given in Section 6. 2. Literature Review on GSA GSA is heuristic optimization technique which is inspired by Newton’s law of gravity. Each agent is named as object and success in optimization algorithm are related as masses in GSA [7]. Using the mass of each agent and distance of between agents are calculated new position of agent. Mass and distance are inversely. Effect of big and close agent is more the solution. While new position of each agent is calculated, to avoid fast convergence is used random number in basic GSA. Main problem of fast convergence is to get stuck of local minimum the method. To overcome fast con- vergence and local minimum, Han and Chang [8] suggested using chaotic variables instead of random numbers in modified GSA. Unconstrained acceleration has caused more diversification in the population. Khajehzadeh et al. [9] proposed velocity clamping for velocities of the agents in order to prevent diversification in the population. Therefore, velocity of the agent is constrained between maximum and minimum values of the velocities. GSA starts to search with random solutions on the search space. An opposition based learning method is pro- posed for the initialization and also continuation working of the GSA by Shaw et al. [10]. In this way, the con- vergence rate of GSA has improved and the robustness of GSA is increased. In order to improve global search ability of GSA, “Disruption” operator, inspired from astrophysics, has been added to basic GSA [11]. The new method is used for optimizing 23 numeric functions and obtained results are compared with basic GSA, PSO and GA. The experimental results show that proposed method is superior to ba- sic GSA, PSO and GA. Li and Zhou [12] developed a new version of GSA by combining the search strategy of PSO and the im- proved GSA (IGSA) is applied to parameters identification of hydraulic turbine governing systems. The experi- mental results show that (IGSA) is capable with respect to PSO, GA and basic GSA in terms of solution quality. Niknama et al. [13] suggested self-adaptive GSA to improve convergence characteristic in basic GSA. Two methods developed to improve solution in this technique. New solution in GSA moves independently the pre- vious solution because GSA has not memory. Finding best solution is used to find new solution in the first tech- nique. Second technique was developed for which solution has not local minimum. New solution was produced using three different agent are selected in second technique. Produced solution was used new solution with probability. In addition, GSA algorithm has been used in many research fields such as clustering [14,15], image enhance- ment [16], classification [17], secure communication [18] and filter modeling [19]. 3. Gravitational Search Algorithm One of the newest heuristic optimizers is gravitational search algorithm (GSA) which is based on law of gravity, law of motion and interaction of masses [7]. In GSA, potential solutions correspond to the position of masses and masses corresponds the fitness value of the solution produced for the optimization problem. By using law of gravity and law of motion, Rashedi et al. [7] have defined interaction between the masses. The GSA is an itera- tive algorithm and the algorithm is explained step by step as follows: Step 1. Initialization The masses are randomly produced on the solution space using Equation (1). ( ) minmax min , 1,2, 1,2,, ij jjj XXrXXiN and jD =+×−= …= … (1) where is the ith mass position value on the jth dimension, and is the upper and lower bound for the jth dimension, respectively, N is the number of masses and D is the dimensionality of the optimi-  O. Findik et al. zation problem. After the random solution is produced, the sizes of the masses are calculated as follows: () () worst best worst () () () i i fit tfitt mt fitt fitt − =− (2) (3) where is the size of inertial mass on the ith position on iteration time t, is the size of the mass which is on the ith position on iteration time t, is the fitness value of the mass on the ith position on iteration time t, and are the best and worst fitness values in the mass population on itera- tion time t. Step 2. Law of Gravity In GSA, interaction between the masses is based on action-reaction. Force acting on a mass is calculated as follows: For each mass i, For each dimension d, ( )( )( )( ) ( )( )( ) ( ) , ,, , 1, 2,, ij d i jidjd ij Mt Mt F tGtXtXt Rt jN ε × =× ×− + = … (4) where is the force acting on dth dimension of masses on ith position on iteration time t, () is the gravitational constant number on iteration time t, and is the active and passive gravitational masses on iteration time t, respectively, is the dth dimension of masses on ith position, is the dth dimension of masses on jth position at iteration time t, is the Euclidian distance between the mass on ith position and the mass on jth position and is the small constant number. After the force for each dimension is calculated using Equation (4), the total force on the mass is obtained as follows: , 1 () () N dd ij ij j Ftr Ft = = × ∑ (5 ) where () is the total force acting on dth dimension of the mass on ith position on iteration time t and is a random number produced in range of [0,1], which is used for providing stochastic characteristic to GSA. Step 3. Law of Motion The motion depends on acceleration of the mass and the acceleration of the mass is calculated as follows: (6) where is the acceleration on the dth dimension of the mass ith position. The velocity and new position of the mass are calculated as follows: ()( ) , 1 () d dd iid ii vtrvt at += ×+ (7) ()( ) 1( 1) d dd i ii XtXt vt+=+ + (8) where is the velocity for dth dimension of the mass on the ith position on iteration time , is the dth dimension of the mass on ith position at iteration time and is the random num- ber produced for dth dimension of the mass ith position in range of [0,1]. Step 4. Termination After new positions for the masses are obtained by using Equations (6)-(8), the fitness of the solutions are 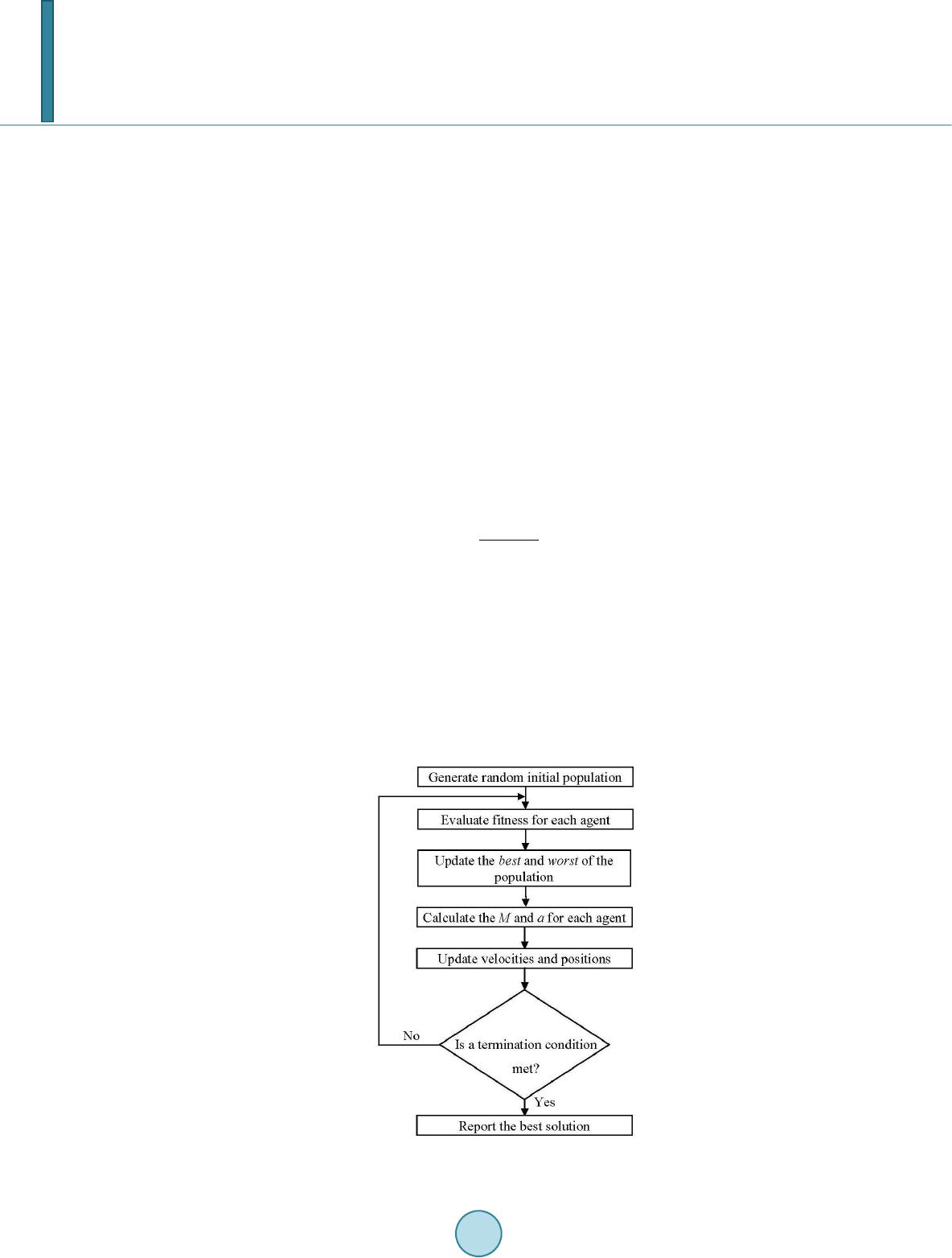 O. Findik et al. calculated using Equations (2) and (3). The obtained solution with best fitness value is stored and if a termina- tion condition is met, the algorithm is terminated and the best solution is reported. Otherwise, running of the al- gorithm is continued from the Step 2. Basic GSA is presented as a flowchart in Figure 1. In the basic GSA, all agents in the population are used for calculating force acted on a mass. In order to in- crease convergence and local search capabilities of the method, which agents will be used are decided for de- termining acting force on a mass by using four selection mechanisms—roulette wheel, tournament, random and rank-based selection mechanisms and these mechanisms are given below. 3.1. Random Selection In order to provide enough diversification in the population, a certain number of particles are selected from the population. Instead of whole population, the selected particles are used for calculating force acting on the mass. In this selection mechanism, each agent has same selection probability and whole solution space is searched by using this mechanism but the local search on the solution space is reduced. 3.2. Roulette Wheel Selection This selection mechanism is based on the fitness of the solutions. For calculating force acting on the mass, a certain number of particles are selected from the population using roulette wheel selection. Being selected probability of a particle is given as follows: (9 ) where is the being selected probability of the ith particle, is the fitness value of the solution of ith par- ticle and N is the number of particles. Being used roulette-wheel selection, it is aimed that the convergence rate of the method is increased because the agent has been affected mostly good solutions obtained previous itera- tion. 3.3. Tournament Selection Tournament selection covers running several tourneys between the particles randomly selected from the popula- tion. The winner of each tourney (the agent with the better fitness) is used for calculating force acting on the Figure 1. The flow chart of the GSA.  O. Findik et al. mass. The tournament size is important for the tournament selection mechanism because if the tournament is larger, weak particles have a smaller chance to be selected. In the tournament selection, when the number of tournament is increased, the agent has been affected mostly the best solution, and the solutions of the population are quickly improved especially for unimodal functions. When the number of tournament is decreased, the solu- tion with low fitness can be selected and the diversity in the population can increase and global search ability of the method is improved. 3.4. Rank-Based Selection Rank-based selection is an alternative selection mechanism used for obtaining chromosomes which will be sub- jected to crossover operation in genetic algorithm [20]. In the rank-based selection, the agents are sorted in as- cending order by using their fitness values. For each rank, a selection probability is calculated as follows: ( 1) 22 (1)( 1) pos Pos pSP SPN − =− +×−×− (10) where, is agent’s probability of being selected in position pos, N is the number of agents and SP is the se- lective pressure. In the positions, position of least fit agent is first order 1 and the position of fittest agent is Nth order. 4. Experimental Results In order to investigate effects of the selection mechanisms to the performance of the GSA, 23 benchmark func- tions taken from [7] are used and obtained results are compared the results of basic GSA. 4.1. Benchmark Functions 23 test functions given in Tables 1-3 and taken from [7] are divided to different groups. F1-F7 functions have only one local minimum and this local minimum is global minimum. These functions are unimodal functions, and used for investigating local search ability of the method. If a function has more than one local minimum, this function is called as multimodal function and the global search capability of the method is tested on these functions (F8-F13). Another difficulty for a method is dimensionality of the optimization problem [21,22]. While F14-F23 test functions are small-sized functions, the dimensionality for F1-F13 functions is taken as 30. 4.2. Control Parameters The population size of the methods is taken as 50 in all experiments. The stopping criterion for the algorithms is Table 1. The unimodal benchmark functions. F.No D Range Function 1 30 [−100,100] 2 30 [−10,10] 211 () DD ii ii Fx xx = = = + ∑∏ 3 30 [−100,100] 2 311 () Di j ij Fx x = = = ∑∑ 4 30 [−100,100] 5 30 [−30,30] ( ) 122 51 1 ( )100(1) D ii i i Fxxxx − + = =− +− ∑ 6 30 [−100,100] 2 61 ( )([0.5]) D i i Fx x = = + ∑ 7 30 [−1.28,1.28] 4 71 ( )[0,1) D i i F xixrandom = = + ∑  O. Findik et al. Table 2. The multimodal benchmark functions. F.No D Range Function 8 30 [−500,500] ( ) 81 ( )sin D ii i Fxxx = = − ∑ 9 30 [−5.12,5.12] ( ) 2 91 ()10cos 210 D ii i Fx xx π = =−+ ∑ 10 30 [−32,32] () 2 10 11 11 ()20exp0.2expcos 220 DD ii ii Fxxx e nn π = = =− −−++ ∑∑ 11 30 [−600,600] 2 11 11 1 ( )cos1 4000 DD i i ii x Fx xi = = =−+ ∑∏ 12 30 [−50,50] ()()()() 122 2 12 11 11 ( )10sin1110sin1(,5,100,4) DD iiD i ii F xyyyyux D πππ − + = = =+−++− + ∑∑ ( ) ( ) ( ) ,,, 0 m ii ii m ii kxa xa u x akmaxa kxax a −> =−< < −−<− 13 30 [−50,50] ()()()()() 22 22 2 131 1 1 ()0.1sin311 sin3111 sin21 ( ,5,100,4) D i iDD i D i i Fxx xxxx ux ππ π = = =+−+++−+++ + ∑ ∑ Table 3. The multimodal benchmark functions with fix dimensions. F.No D Range Function 14 2 [−65.53,65.53] 1 25 2 14 11 11 () 5000 ( ji ij i Fx j xa − == = + +− ∑∑ 15 4 [−5,5] ( ) 2 2 11 12 15 2 134 () ii i iii x bbx Fxa b bx x = + = − ++ ∑ 16 2 [−5,5] 24624 161111 222 1 ( )42.144 3 F xxxxxxxx=−+ +−+ 17 2 [−5,10] × [0,15] 2 2 172111 2 5.1 51 ()6101cos()10 48 Fxxxxx ππ π =−+ −+−+ 18 2 [−5,5] ( ) ( ) ( ) ( ) 222 18121121 22 222 1 2112122 ( )11191431463 302318 3212483627 F xxxxxxxxx x xxxxxxx =+ ++−+−++ × +−×−++−+ 19 3 [0,1] ( ) 43 2 19 11 ( )exp iijjij ij Fxcaxp = = =− −− ∑∑ 20 6 [0,1] ( ) 46 2 20 11 ( )exp iijjij ij Fxcax p = = =− −− ∑∑ 21 4 [0,10] ( )( ) 51 21 1 1 () T ii i Fxxa xac − = =−− −+ ∑ 22 4 [0,10] ( )()() 71 22 1 T i ii i Fxxaxac − = =−−−+ ∑ 23 4 [0,10] ( )( ) 10 1 23 1 1 () T ii i Fxxa xac − = =−− −+ ∑  O. Findik et al. maximum iteration number (MIN), and MIN is 1000 for F1-F13 functions and 500 for F14-F23 functions. The gravitation constant (G) used in GSA depends on iteration time and is calculated as follows [7]: (11 ) where is the gravitation constant at time step t, is the initial gravitation constant which is taken as 100 in the initialization of the algorithm, is the maximum iteration number and is scaling factor and it is set to 20. Number of masses which will be act force is taken as 10, 15, 20, 25, 30, 35 and 40 in GSAF (GSA with rou- lette wheel selection), GSAT (GSA with tournament selection), GSAR (GSA with random selection), GSAL (GSA with rank-based selection). Experimental studies show that the more successful results are obtained when the number of masses which will be act is taken as 40. Therefore, the number of masses which will be act is taken as 40 in the comparisons. In GSA with rank-based selection mechanism, the linear ranking is used and the selective pressure is taken as 2. 4.3. Compar isons The mean results obtained by GSAF, GSAT and GSAR, GSAL are compared the mean results of basic GSA and these results are presented in Table 4 for unimodal test functions, Table 5 for multimodal functions and Table 6 for the multimodal test functions with fix dimension. According to Table 4, the results obtained by GSAR and GSAF methods are relatively better than the results of basic GSA because these functions are unimodal functions and the local search ability of the GSAF and GSAR is better than GSA. Based on Table 5, due to the fact that the masses in basic GSA have been affected by all the masses in the population, the diversity in the population is kept during the iterations and the results obtained by basic GSA are slightly better than the results of proposed methods. Table 4. The comparison of the methods on the unimodal test functions. Func. Methods GSA GSAR GSAF GSAT GSAL F1 7.3E−11 3.4E−16 3.45E−16 3.48E−16 4.25E−16 F2 4.03E−5 8.18E−08 8.06E−08 8.39E−08 8.8E−08 F3 0.16E+3 111.9831 109.9879 114.1624 17.6635 F4 3.7E−6 7.93E−09 7.93E−09 0.029325 8.86E−09 F5 25.16 26.07533 29.79962 30.11498 25.4512 F6 8.3E−11 0 0 0 0 F7 0.018 0.035454 0.031632 0.030072 0.032517 Table 5. The comparison of the methods on multimodal test functions. Func. Methods GSA GSAR GSAF GSAT GSAL F8 −2.8E+3 −2778.19 −2854.1 −2786.07 −2949.51 F9 15.32 21.45794 22.38657 25.66993 26.66489 F10 6.9E−6 1.42E−08 1.42E−08 1.43E−08 1.56E−08 F11 0.29 1.469172 1.67303 1.3961 0.649063 F12 0.01 0.030507 0.058855 0.044521 2.56E−18 F13 3.2E−32 3.98E−17 3.57E−17 3.64E−17 4.12E−17  O. Findik et al. Table 6. The comparison of the methods on the multimodal test functions with fix dimension. Func. Methods GSA GSAR GSAF GSAT GSAL F14 3.70 5.307424 1.996672 56.55266 3.3022 F15 8.0E−3 0.004322 0.004202 0.00765 0.0020 F16 −1.03163 −1.03163 −1.03163 −1.02012 −1.03163 F17 0.3979 0.39789 0.3979 0.416527 0.3979 F18 3 3 3 3.243807 3 F19 −3.7357 −3.8603 −3.8628 −3.82561 −3.8628 F20 −2.0569 −3.322 −3.31792 −2.86047 −3.3220 F21 −6.0748 −6.15111 −5.39355 −2.49662 −6.4399 F22 −9.3389 −10.4029 −8.92953 −2.05354 −9.9150 F23 −9.45 −10.5364 −9.33603 −2.11848 −10.5364 According to Table 6, the dimensionality is the important factor for the methods and the proposed methods are better than the basic GSA, except GSAT. In the GSAT, masses have been affected from the same mass and the diversity in the population has been lost and this has caused the stagnation of the population. This situation is balanced in other selection mechanisms by using fitness values or randomness. 5. Results and Discussion In this study, we used four selection mechanisms- roulette wheel, tournament, random and rank-based selections and obtained the better results than GSA. Experimental results show that the selection mechanisms directly af- fect the performance of GSA because to obtain a new position for the agent in GSA is important for the perfor- mance of GSA. For the population-based heuristic approaches, information sharing and interaction between the agents describe behavior of the method and to be selected the agents using their fitness values provides to obtain high quality solutions for the numerical benchmark functions. Experimental results show that fitness-based se- lection mechanisms such as roulette-wheel and tournament is appropriate for the unimodal and multimodal functions with fix dimension, but for multimodal functions with huge local minimums these mechanisms have caused early saturation of the population, to lost diversification in the population and to get stuck of local mini- mums. Therefore, the random, rank-based selection mechanisms are more appropriate for solving the multimod- al functions instead of fitness-based selection mechanisms. But it should be mentioned that the random selection mechanism can cause the slow convergence to the optimum or optimums and reduce the local search ability of the method. The effect of the selection mechanism used for generating new chromosomes is known on the Ge- netic algorithm in the literature but in this study, the effect of selection mechanism for the GSA has been inves- tigated and obtained results are used for comparing and discussion. In GSA, the selection techniques do not have the same effect with the GA because velocity updating equation of GSA does not work likewise crossover of GA. The obtained results show that the proposed techniques for GSA have positive effect on solving the numer- ical function. Consequently, it is shown that the solution quality is improved by using selection mechanism in original GSA and, the suitable selection mechanism for GSA should be used in order to obtain more quality so- lution depending on structure of the optimization problem. 6. Conclusion and Future Works We analyzed four selection mechanisms for the GSA on the 23 benchmark functions based on solution quality. The experimental results show that using the appropriate selection mechanism provides to obtain the quality so- lutions. Because GSA with the selection mechanism has high performance on the continuous optimization prob- lems, our future works include applications of proposed method in various optimization problems.  O. Findik et al. Acknowledgements This study has been supported by Scientific Research Project of Selçuk University. References [1] Kennedy, J. and Eberhart, R.C. (1995) Particle Swarm Optimization. Proceedings of International Conference on Neu- ral Networks, 4, 1942-1948. http://dx.doi.org/10.1109/ICNN.1995.488968 [2] Dorigo, M., Maniezzo, V. and Colorni, A. (1996) The Ant System: Optimization by a Colony of Cooperating Agents. IEEE Transactions on Systems, Man, and Cybernetics—Part B, 26, 1-13. [3] Pham, D.T., Ghanbarzadeh, A., Koc, E., Otri, S., Rahim, S. and Zaidi, M. (2006) The Bees Algorithm: A Novel Tool for Complex Optimisation Problems. Proceedings of Intelligent Production Machines and Systems (IPROMS) Confer- ence, 454-459. [4] Karaboga, D. and Basturk, B. (2007) A Powerful and Efficient Algorithm for Numerical Function Optimization: Ar- tificial Bee Colony (ABC) Algorithm. Journal of Global Optimization, 39, 459-171. http://dx.doi.org/10.1007/s10898-007-9149-x [5] Geem, Z.W., Kim, J.H. and Loganathan, G.V. (2001) A New Heuristic Optimization Algorithm: Harmony Search. Si- mulation, 76, 60-68. http://dx.doi.org/10.1177/003754970107600201 [6] Holland, J.H. (1975) Adaptation in Natural and Artificial Systems. The University of Michigan Press, Ann Arbor. [7] Rashedi, E., Nezamabadi-Pour, H. and Saryazdi, S. (2009) GSA: A Gravitational Search Algorithm. Information Sci- ences, 179, 2232-2248. http://dx.doi.org/10.1016/j.ins.2009.03.004 [8] Han, X. and Chang, X. (2012) A Chaotic Digital Secure Communication Based on a Modified Gravitational Search Algorithm Filter. Information Sciences, 208, 14-27. http://dx.doi.org/10.1016/j.ins.2012.04.039 [9] Khajehzadeh, M. , Taha, M. R., El-Shafie, A. and Eslami, M. (2012) A Modified Gravitational Search Algorithm for Slope Stability Analysis. Engineering Applications of Artificial Intelligence, 25, 1589-1597. http://dx.doi.org/10.1016/j.engappai.2012.01.011 [10] Shaw, B., Mukherjee, V. and Ghoshal, S.P. (2012) A Novel Opposition-Based Gravitational Search Algorithm for Combined Economic and Emission Dispatch Problems of Power Systems. Electrical Power and Energy Systems, 35, 21-33. http://dx.doi.org/10.1016/j.ijepes.2011.08.012 [11] Sarafrazi, S., Nezamabadi-Pour, H. and Saryazdi, S. (2011) Disruption: A New Operator in Gravitational Search Algo- rithm. Scientia Iranica, 18, 539-548. http://dx.doi.org/10.1016/j.scient.2011.04.003 [12] Li, C. and Zhou, J. (2011) Parameters Identification of Hydraulic Turbine Governing System Using Improved Gravita- tional Search Algorithm. Energy Conversion and Management, 52, 374-381. http://dx.doi.org/10.1016/j.enconman.2010.07.012 [13] Niknama, T., Golestaneh, F. and Malekpour, A. (2012) Probabilistic Energy and Operation Management of a Micro- grid Containing Wind/Photovoltaic/Fuel Cell Generation and Energy Storage Devices Based on Point Estimate Method and Self-Adaptive Gravitational Search Algorithm. Energy, 43, 427-437. http://dx.doi.org/10.1016/j.energy.2012.03.064 [14] Yin, M., Hu, Y., Yang, F., Li, X. and Gu, W. (2011) A Novel Hybrid K-Harmonic Means and Gravitational Search Algorithm Approach for Clustering. Expert Systems with Applications, 38, 9319-9324. http://dx.doi.org/10.1016/j.eswa.2011.01.018 [15] Hatamloua, A., Abdullah, S. and Nezamabadi-pour, H. (2012) A Combined Approach for Clustering Based on K- Means and Gravitational Search Algorithms. Swarm and Evolutionary Computation, 6, 47-52. http://dx.doi.org/10.1016/j.swevo.2012.02.003 [16] Zhao, W. (2011) Adaptive Image Enhancement Based on Gravitational Search Algorithm. Procedia Engineering, 15, 3288-3292. http://dx.doi.org/10.1016/j.proeng.2011.08.617 [17] Bahrololoum, A., Nezamabadi-pour, H., Bahrololoum, H. and Saeed, M. (2012) A Prototype Classifier Based on Gra- vitational Search Algorithm. Applied Soft Computing, 12, 819-825. http://dx.doi.org/10.1016/j.asoc.2011.10.008 [18] Han, X. and Chang, X. (2012) Chaotic Secure Communication Based on a Gravitational Search Algorithm Filter. En- gineering Applications of Artificial Intelligence, 25, 766-774. http://dx.doi.org/10.1016/j.engappai.2012.01.014 [19] Rashedi, E., Nezama badi-pour, H. and Saryazdi, S. (2011) Filter Modeling Using Gravitational Search Algorithm. En- gineering Applications of Artificial Intelligence, 24, 117-122. http://dx.doi.org/10.1016/j.engappai.2010.05.007 [20] Pohlheimi, H. (2006) GEATbx: Genetic and Evolutionary Algorithm Toolbox for Use with MATLAB Documentation. http://www.geatbx.com/docu/index.html  O. Findik et al. [21] Boyer, D.O., Martinez, C.H. and Pedrajas, N.G. (2005) Crossover Operator for Evolutionary Algorithms Based on Population Features. Journal of Artificial Intelligence Research, 24, 1-48. [22] Karaboga, D. and Akay, B. (2009) A Comparative Study of Artificial Bee Colony Algorithm. Applied Mathematics and Computation, 214, 108-132. http://dx.doi.org/10.1016/j.amc.2009.03.090
|