 Journal of Computer and Communications, 2014, 2, 99-107 Published Online March 2014 in SciRes. http://www.scirp.org/journal/jcc http://dx.doi.org/10.4236/jcc.2014.24014 How to cite this paper: Eldem, H. and Ülker, E. (2014) Application of Ant Colony Optimization for the Solution of 3 Dimen- sional Cuboid Structures. Journal of Computer and Communications, 2, 99-107. http://dx.doi.org/10.4236/jcc.2014.24014 Application of Ant Colony Optimization for the Solution of 3 Dimensional Cuboid Structures Hüseyin Eldem1, Erkan Ülker2 1Computer Technologies Department, Karamanoğlu Mehmetbey University, Karaman, Turkey 2Computer Engineering Department, Selçuk University, Konya, Turkey Email: heldem@kmu.edu.tr, eulker@selcuk.edu.tr Received Novembe r 2013 Abstract Traveling Salesman Problem (TSP) is on e of the most wide ly studied real world problems of find- ing the shortest (minimum cost) possible route that v isit s each node in a given set of nodes (citie s ) once and then returns to origin cit y. The optimization of c uboid ar eas has potential samples that can be adapted to real world. Cuboid surfaces of bui lding s, rooms, furniture e tc. can be g iven as examples. Many optimization algori thm s have been used in solution of optimization problems at present . Among them, meta-heuristic algorithms come first . In this study, ant colony optimization, one of meta-heuristic methods, is applied to solve Eucli dian TSP con sistin g of ni ne diffe rent sized sets of nodes randomly placed on a cuboid surface. The performance of this method is shown in tests. Keywords Euclidean TSP; Ant Colony Optimiz ati on; Metaheuristic; Path-Relinking; Path Planning; Cuboid 1. Introduction Traveling salesman problem (TSP) is a well-known problem in combinatorial optimization and it has been widely studied in the theoretical computer science and engineering applications. It is a problem that has to be solved by a salesman who travels between cities at minimum cost and return to the origin city. In this problem, one of the parameters including cos t, time and pa th is optimized. The problem can also be stated as a Hamilto- nian cycle problem used in data modeling in computer sciences and investigated in the scope of a graph the ory. Since 1950s, ma n y r esearchers (e.g. computer scientists, mathematicians and others) have studied to develop methods that solve TSP finding the shortest route for c ities in a given collection. If all costs between two cities are equal for both cities, TSP is named as symmetric , and otherwise, it is called asymmetric TSP. TSP applications are fr equently en coun tered in transportation systems. A b us rou te collectin g passengers at certain bus stops can be organized as TSP. Developing effective TSP solutions is gradually gaining importance in route planning problems such as airways, delivery trucks, mail carr iers and computer networks.  H. Eldem, E. Ülker TSP, which is evaluated in the area of discrete and combinatorial problems, has been widely studied in the area of similar popular problems. In the symmetr i c TSP, the distance b etween cities i and j is the same, i.e., dij = dji. In the asymme t r i c TSP, this rul e may not be valid all the time. Eu clidean TS P is special cases of symmetr ic TSP where the cities are positioned in Rm space f or some m values for which the cost functio n satisfies the trian- gle equation. The ℓm norm, Euclidean norm if m = 2, is defined as for and (x1,···xm), (y1,…ym) . Two-dimensional Euclidean TSP is a popular an d w idely studied issue [1]. There are a great number of publications in literature devoted to TSP solution. Various heuristic algorithms, which give the possible closest solutions to the best ones in a certain time, based on simulated annealing [2], genetic algorithms (GA) [3-5], tabu search [6,7], artificial neural networks [8-10] an d ant colony systems [11-16] have been developed. Meanwhile, local search algorithms like 2-opt and 3-opt were also used to so lv e TSP [17]. In order to attain better results, some researchers tried hybrid evolutionary algorithms [18-21]. Lately, 2-dimen- sional TSP problem has been transferred to the 3rd dimension and studied in liter atur e. In [22-24], TSP applica- tions were performed for the points on 3D geometric shapes like sphere and cuboid. New algorithms were de- veloped through using genetic algorithms for TSP solution on cuboid geometric shape [22], Particle Swarm Op- timization (PSO) on cuboid shape [23] and genetic algorithms on 3D sphere shape [24]. Ant colony optimization (ACO), one of metaheuristic algorithms used to solve optimization problems, was proposed as a PhD thesis by Marco Dorigo in 1992 [15]. It is a probabilistic technique that is used to solve computational problems by investigating the probable ways on the graphs. It originates from the behavior of ants that find the shor t est distance between their n ests an d the food sou rc e while seeking food and rapidly choose the shorter path. Various TSP applicatio ns were successfully solved by means of ACO techniques. In the propos ed study, TSP for points on a cuboid shape is solved by ACO algorithm. As 2-dimensional TSP is a difficult problem and its reasons are given in the previous studies in literature, the fact that 3D TSP is a dif- ficult problem is not proved in this study. To the knowledge of the author, there is no study in litera tur e that solves 3D TSP with ACO. In the existing TSP problems, coordinates or distances of points are known. The problem in this study differs from the existing TSP pr oble ms in that all points are located on a cuboid shape and the transition between points can be made through cuboid surface [22]. The developed 2D Euclidian TSP me- thods could be directly applied to 3D TSP with poin ts in 3D space. However, TSP on a cuboid shape is different from 3D TSP as minimum distances between points on different surfaces cannot be calculated with Euclidian distance. As the travel takes places on the surfaces of cuboid, rou tes should be formed on the surfaces, as well, and not within the cuboid. The solutions cou l d be used in route planning and collecting and placing pieces dur- ing the creation of a cuboid structure. This o ptimizatio n me thod might be needed for small robot agents climb- ing up the wall, rou t e planning, cleaning and painting . In this study, the performance of the developed method using ACO is tested, also its comparison with GA selected from the literature and advantages are presented. Pri- marily, the definitions of points on cuboid surface and determination of distances between points are explained. Subsequently, the adaptation of the problem to ACO is explained in the further p arts of the paper. 2. Description of Cuboid Shapes Cuboid is geometric shape which can be frequently seen in various products including wooden, metal, plastic and paper boxes, books, toys, dice, cupboa rds, furn i tur e , rooms and buildings. Cuboid is a three-dimensional object and a geo metric shape with six rectangular faces (Figure 1). It has six faces, twelve side s a nd eigh t co rn e rs . Among geometric shap es, rectangular prism has a cuboid shape. Among three-dimensional objects, cub e is a special form of cuboid, consisting of all square faces. As can be seen in Figure 1, cuboid is one of the three-dimensional objects with height, width and leng th. Cuboid objects have six faces: b ack (S0), bottom (S1), left (S2), front (S3), top (S4) and right (S5) (Figure 2). Geometric information about a cuboid object located as back face z = 0, bottom y = 0 an d left x = 0 is given in Table 1. There are four sid e s and four corners for each face and some side s and co r n ers are shared among the rectangles forming the face (Table 1). N points could be present on any of 6 cuboid faces. N = 7 cities (c0, c1, c2, c3, c4, c5, and c6) could be located on cuboid faces (S3, S1, S5, S4, S4, S0, and S2) as in Figure 3. The Euclidean distance of a pair of cities ci (xi, yi, zi) and cj (xj, yj, zj), is notated as dij (i,j = 1···n). Then the distances between all pairs of cities can be computed in an N x N symmetr i c d istanc e matrix D = [dij]. For a pair of cities on the cuboid, there are three possibilities : a) both on the same face; b) two cities on opposite faces; c) 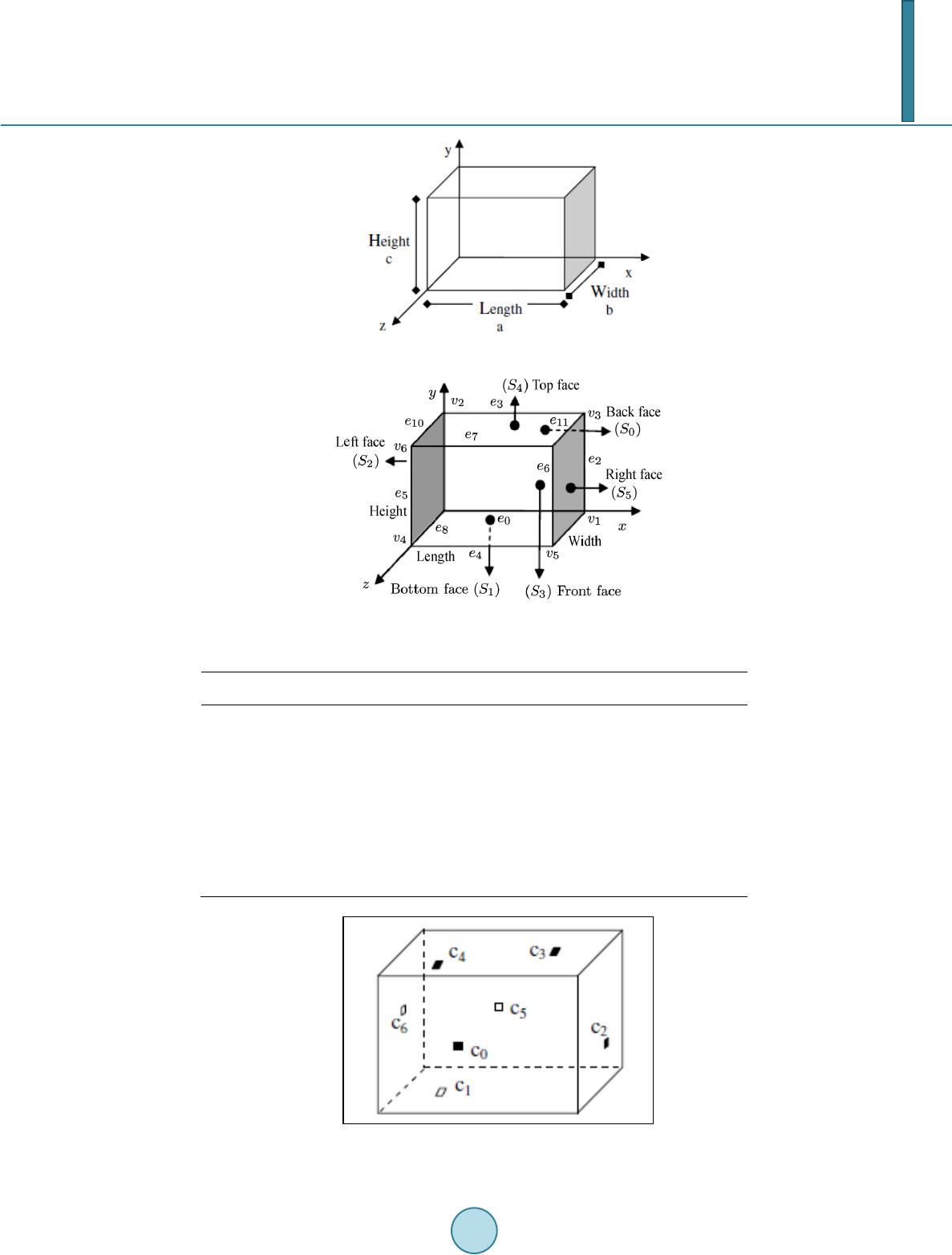 H. Eldem, E. Ülker Figure 1. A cuboid shape. Figure 2. A cuboid object. Table 1. Geometri cal da ta of a cuboid. Faces x y z Vertices Edges S0 (Back Face) 0 < x < Length 0 < y < Height 0 0,1,3,2 0,2,3,1 S1 (Bottom Face) 0 < x < Length 0 0 < z < Width 0,4,5,1 0,8,4,9 S2 (Left Face) 0 0 < y < Height 0 < z < Width 0,2,6,4 1,10,5,8 S3 (Front Face) 0 < x < Length 0 < y < Height Width 4,5,7,6 4,6,7,5 S4 (Top Face) 0 < x < Length Height 0 < z < Width 2,3,7 ,6 3,11,7,10 S5 (Right Face) Length 0 < y < Height 0 < z < Width 1,3,7,5 2,11,6,9 Figure 3. View of seven points on cuboid faces.  H. Eldem, E. Ülker two cities on adj acent faces. The pseudo code use d for calculating the distan ce between ci and cj points is given below: if (face(ci) == face(cj))//SAME FACE { dij = Euclidean distance between the two points; } else if (face(ci) (opposite) face(cj))//OPPOSITE { calculate four alternative pa th distances di (through remaining faces) dij = d0; for(int k = 0; k < 4; ++k) if(dk < dij) dij = dk; } else if (face(ci) (adjacent) face(cj))//ADJ ACEN T { d0 = calculate distance between the two points (through common edge of faces containing c1 and c2); d1 = calculate distance between the two points (through the first common adjacent face of c1 and c2); d2 = calculate distance between the two points (through the second common adjacent face of c1 and c2); dij = min(d0, d1, d2); } The detailed information about pseudocode above used for calculating the distance between two points on cuboid faces is as follows: a) If t w o cities are on the same face: Euclidean distance between two points is computed directly by 222 (x-x) (y-y) (z-z) jiji ji ++ . Th e combinations are {S0, S0}, {S1, S1}, {S2, S2}, {S3, S3}, {S4, S4} and {S5, S5} for any city pairs ci and cj. b) If two cities are on the opposite faces: There are three alternatives in this case. 1) Front-Back {S3, S0}, 2) Left-Right {S2, S5} and (3) Bottom-Top {S1, S4}. Four possible routes must be calculated for measuring the dis- tance between opposite faces and the shortest path must be chosen. For instance, the possible routes for Left- Right case are: I) Left-Front-Right II) Left-Back-Right III) Left-Top-Righ t IV) Left-Bottom-Right In this case, the possible routes (d1, d2, d3 and d4) can be calculated, respectively, as follows: for alternative (I) (width) length(width) zj i dz z=−+ +− The routes can be similarly calculated for the other two cases mentioned above. c) If two cities are on neighboring (adjacent) faces: The re are again four altern ative r oute s b etween adja- cent faces in this case. However, if anoth er face is visited for calculating the distance between adjacent faces, this alternative is neglected in calculations as it is the longest. For instance, for Front-Bottom neighboring faces, 1) Front-Bottom, 2) Front-Right-Bottom, 3) Front-Left-Bottom, and 4) Front-Top-Back-Bottom alterna tives must be calculated. However, as the nonneighboring Top and Back faces are present for Front-Bottom trans ition in 4) Front -Top-Bottom alternative, it is not taken into consideration and neglected. In this case, the possible al- ternative routes (d1, d2 and d3) are calculated, respectively, as follows, and then, the shortest route is chosen . for alternative (I)  H. Eldem, E. Ülker There are 12 alternatives as neighboring faces: (Back-Bottom), (Back-Left), (Back-Top), (Back-Right), (Bot- tom-Left), (Bottom-Front), (Bottom-Right), (Left-Front), (Left-Top), (Front-Top), (Front-Right) and (Top- Right). The distance of each combination can be computed in a similar way by considering axis differences. 3. The Solution of TSP on a Cuboid Object by Using ACO 3D TSP that would be applied to the surface of the cuboid is different from normal 2D TSP [22]. The salesman (ant or robot) could only travel between points located on th e surface of the cuboid. The only difference in this problem is that the points are not located in the cuboid but on the surface of the cuboid. The problem to be solved can be defined as the determination of the minimum tour distance for a salesman (ant) to trave l a ll points (N points in total with known coordinates) located on a surface of a cuboid and come back to the original point, similar to standard TSP. In this study, it is aimed to solve the depicted problem by ACO method. After creating a distance matrix consisting of each pair of points, problem solution becomes the same as stan- dard TSP. After this stage, the solution of the problem can be examined by each method to solve TSP, which is depicted in the literature survey of the introduction p art. In this paper, solutio ns were obtained for specific num- ber of set of points by using ACO. General structure of the ACO: initialize all edges to (small) initial pheromone level τ0; place each ant on a randomly chosen city; for each itera tio n do: do while each ant has not completed its tour: for each an t do: move ant to next city by the probability fun ction and roulette wheel selection end; end; for each an t with a complete tour do: evaporate pheromones; apply pheromone update; if (ant k’s tour is shorter than the global solution) update global solution to ant k’s tour end end Based on this general structure, initial values of ACO algorithm are set. Accordingly, initial pheromone loads of each side are updated and stored in pheromone matrix. Using the notations in Title 2, distance matrix consist- ing of distances between each point and every other point is created. In ACO algorithm, each ant giving solution, i.e., agent ant is located random cities initially. In each iteration, the following Equation (1) is used to select the next city to be visited by ants. ( )( ) ( ) [ ] .if j allowed. . ij ij k ij k ik ik t pt t β α αβ τη τη = ∈ ∑ (1) where, is the density of the mark left at the edge at a time, t. The value of , i.e., visibility, is equal to 1/dij. dij, is the distance between two points on a cuboid. α and β are two parameters which control the impor- tance of pheromone relative to the visibility. Af ter ants complete their tour s, i.e., after each ant finds its solution, evaporation of pheromone and updating processes are performed. By means of evaporation, it could be possible to forget the wrong solutions and give opportunity to the new tours by preventing the accumulation of phero- mone. Meanwhile, the best solution given by ants is the one that yields the best displacement globally and give  H. Eldem, E. Ülker the best r esults wh en the iter ations are complete. 4. Experimental Res ults Analyses were performed in a computer of Intel Core 2 Duo P8700 2.53 GHz processor and 4 GB RAM. In coding phase of the method, Matlab R20 10 a programming language was used and called cuboidTSP software. The simulation results obtained through this software were produced for the points N = 10, 50, 100, 250 on a 1000 × 1000 × 1000 cubo id. Simulations were repeated 100-times for each value of N. A new random point set was generated for each trial. In this study, this approach was preferred instead of the method given in [22], i.e., utilization of th e predefined set of points to generalize the results on the cuboid. The performance of the suggested method was compared to the results reported by [22]. In [22], Aybars reported results for five different GA generation sizes (20, 40, 60, 80, 100) and the points of N = 10, 50, 100, and 250 for TSP application on cuboid through GA. For each generation, Aybars fixed the size of the population as 250. While the mutations of individuals in a population observed in each generation can be defined as evolution, the total evolution is equal to multiplication of the size of the population by the number of generation. In the literature, for the solution of TSP, it is convenient to take the number of ants to the number of cities. For this reason, in the proposed study, the number of ant was taken equal to the number of points in the cuboidTSP. In order to make a comparison with a GA publication taken from the literature and to have an equal number of evolutions for ACO with tha t depicted in the [22] for each generation, the number of tour is determined by using the following equation: GenerationSize PopulationSize Numberof Tours. Numberof Ants GA GA ACO ACO × = (2) The r esults r epres en ting the optimum length of th e tour were obtained for different number of evolutions, i.e., 20, 40, 60, 80 and 100 evolutions. For all experiments, the number of ants were equal to that of points and α = 1, β = 5 and ρ = 0.50 (the coeffic ient of evaporati on) were kept constant. The calculated average tour distances both for GA and for the proposed ACO approach are given in Table 2. Mean wh ile, mean calculation durations advised for ACO in this paper are shown in Table 3. The width, height and length of the cuboid were all taken as 1000. A cuboid of 1000 × 1000 × 1000 size is preferred for the sak e of unders tandab ility and easy assessment of the results. When the results of GA and those of ACO were compared, see in Table 2, it was observed that the results of ACO algorithm were much more successful than GA for cuboidTSP. For instance, wh e n evolution number for 150 points is taken as 100, the tour length obtained with GA could be shortened by 1/3. This rate is even higher for 200 and 250 points. It can be seen in Figure 4 that tour lengths are within [5000, 30,000] for GA and [2 000, 10,000] for ACO. Through increasing the numbers of tour and evolution in algorithm, the optimum results can be further im- proved, as can be seen in Table 2 and Figure 4. ACO paramete rs are kept constant in the study. By altering the ACO parameters, better results can be obtained . Apart from ACO, th e results can also be improved through using available hybrid methods for TSP solution. Table 2. Calculated average cuboidTSP tour lengths with GA [22] and ACO for N = 10, 50, 100, 250 points on the surface of the cuboid. Evaluation number 10 50 100 GA ACO GA ACO GA ACO GA ACO 20 5805 3138 12,631 4755 17,938 6340 28,612 9588 40 5805 3027 12,614 4731 17,894 6135 28,430 9138 60 5805 3016 12,609 4653 17,874 6083 28,347 9011 80 5805 2971 12,602 4614 17,853 6055 28,293 8906 100 5805 2942 12598 4603 17845 6039 28252 8818 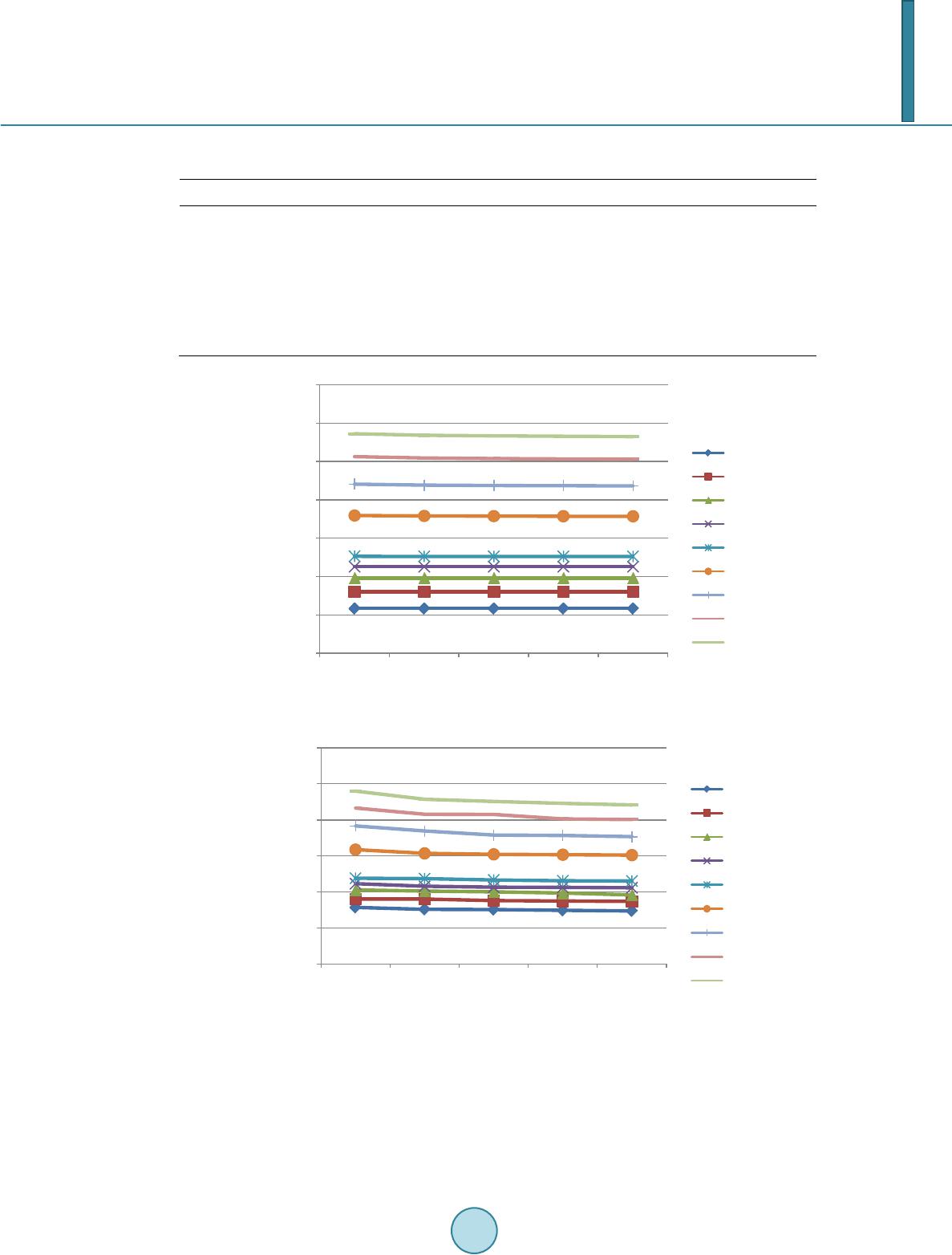 H. Eldem, E. Ülker Table 3. Calculated average cuboidTSP tour computation times with ACO for N = 10, 50, 100, 250 points on the surface of the cuboid. 10 50 100 250 Evolution Number Time (sec) Time (sec) Time (sec) Time (sec) 20 2,652,881 1,606,229 3,847,8 99 1,469,927 40 5,106,337 315,917 7,626,159 2,891,988 60 7,788,457 4,778,198 1,156,2 68 4,416,729 80 1,052,052 6,570,665 1,587,0 84 5,872,519 100 1,388,971 867,242 2,096,042 7,254 ,0 03 (a) (b) Figure 4. Average tour lengths for different amount points on the surface of the cuboid founded by GA [22] and ACO solutions. 5. Conclusion The main contribu tion of this paper is to show the applicability of TSP solutions cuboid objects and structures of 0 5000 10000 15000 20000 25000 30000 35000 0 2000 4000 6000 8000 10000 12000  H. Eldem, E. Ülker any size. The aim of the study is to develop a simple yet effective method through testing ACO method frequently used in T SP problems to determine optimum route by visiting all points on cuboid. For thi s purpose, TSP opti- mization results for different-sized point sets were obtained in the first place through ACO method for points on a cuboid object. It is quite important for saving from time in route planning of air veh icles like helicopter in search and rescue operations on cuboid structures during natural disasters like fire or earthquake. Furthermore, the successful op- timization of the method could be used in maintenance (painting etc.) or cleaning operations on cuboid structures. This method can be used in any kind of applications requiring the use of programmable wall climbing robots. It is possible that 3D applications of TSP problems will become more important with the advancement of robotic in- dustry in the future. The current optimization techniques in literature have been generall y developed in 2D environments. Devel- oping and using these techniques in 3D environments will definitely inspire the development of optimization techniques in different fields. And it is observed that 3D techniques are gradually started to be developed. ACO, which can be effectively used in the solution of current 2D TSP by giving optimum results, was also successful for cuboidTSP. When the results of TSP application on cuboid proposed by Aybars in [22] using GA and the results of the method proposed in the current study are compared, it is seen that ACO provides more successful results in cuboid TS P than GA. In the future stud ies, other methods in the solution of TSP, e.g. PS O, can be tested for the solution of the cu- boidTSP. Meanwhile, cuboidTSP problems can be studied by hybrid utilization of ACO and PSO methods. References [1] Arora, S. (1996) Polynomial T ime Approximation Schemes for Euclidean TSP and Other Geometric Problems. Pro- ceedings of the 37th Annual IEEE Symposium on Foundations of Computer Science, Burlington, 14-16 October 1996, 2-11. [2] Kirkpatrick, S., Gelatt, C.D. and Vecchi M.P. (1983) Optimization by Simula ted Annealing. Science, 220, 671-680. http://dx.doi.org/10.1126/science.220.4598.671 [3] Tsujimura, Y. and Gen, M. (1998) Entropy-Based Genetic Algorithm for Solvi ng TSP. Knowledge-Based Intelligent Electronic Sy stem s, Adelaide, 285-290. [4] Goldberg, D.E. (1989) Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley, Reading. [5] Holland, J.H. (1975) Adaptation in Natural and Artificial System s. University of Michigan Press, Ann Arbor. [6] Glover, F. (1989) Tabu Search—Part I. ORSA Journal on Computing, 1, 190-206. http://dx.doi.org/10.1287/ijoc.1.3.190 [7] Glover, F. (1990) Tabu Search—Part II. ORSA Journal on Computing, 2, 4-32. http://dx.doi.org/10.1287/ijoc.1.3.190 [8] Hopfield, J. J. and Tank, D.W. (1985) Neural Computation of Decisions in Optimization Problems. Biological Cyber- netics, 52, 141-152. [9] Kohonen, T. (1995) Self-Organizing Maps. Springer, Berlin. http://dx.doi.org/10.1007/978-3-642-97610-0 [10] Shinozawa, K., Uchiy ama, T. and Shimohara, K. (1991) An Approach for Solving Dyna mi c TSPs Using Neural Net- works. Proceedings of the IEEE International Joint Conference on Neural Networks, 3, 2450-2454. [11] Colorni, A., Dorigo, M. and Mani ezzo, V. (1991) Distributed Optimization by Ant Colonies. In: Varela, F. and Bour- gine, P., Eds., Proceedings of the European Conference on Artificial Life, ECAL’91, Pari s, Elsevier Publishing, Ams- terdam, 134-142. [12] Colorni, A., Dorigo, M. and Maniezzo, V. (1992) An Investigation of Some Properties of an Ant Algorithm. In: Maenner, R. a nd Manderick, B. , Eds., Proceedings of the Second Conference on Parallel Problem Solving from Na- ture, Brussels, PPSN II, North-Holland, Amste rdam, 509- 520. [13] Dorigo, M. (1992) Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Politecnico di Milano, Italy. [14] Gambardella, L.M . and Dorigo, M. (1996) Solving Sy mmetr ic and Asy mmetr ic TSPs by Ant Colonies. Proceedings of the International Conference on Evolutionary Computation, Nagoya, 20-22 May 1996, 622-627. [15] Dorigo, M. and Gambardella, L.M. (1997) Ant Colony Sy st e m: A Cooperative Learning Approach to the Traveling Salesman Problem. IEEE Transactıons on Evolutıonary Computatıon, 53-66. [16] Dorigo, M. and Gambardella L.M. (1997) Ant Colonies for t he Travelling Salesman Problem. Biosystems, 43, 73-81. http://dx.doi.org/10.1016/S0303-2647(97)01708-5  H. Eldem, E. Ülker [17] Johnson, D. S. and McGeoch, L.A. (1997) The Traveling Salesman Problem: A Ca se Study in Local Optimizati on. In: Aarts, E.H.L. and Lenstra, J.K., Eds., L ocal Search in Combinatorial Optimization, John Wiley & Sons, New York, 215-310. [18] Lee, Z.J. (2004) A Hy bri d Algorithm Applied to Travelling Salesman Problem. Networking, Sensing and Control, Pro- ceedings of the IEEE International Conference, 237-242. [19] White, C.M. and Yen, G.G. (2004) A Hybrid Evolutionary Algorithm for Traveling Salesma n Problem. Congress on Evolutionary Computation (CEC2004), 1473-1478. [20] Marinakis, Y., Migdalas, A. and Pardalos, P.M. (2005) A Hybrid Genetic-GRASP Algorithm Using Lagrangean Re- laxation for the Traveling Sale sman Problem. Journal of Combinatorial Optimization, 10, 311-326. http://dx.doi.org/10.1007/s10878-005-4921-7 [21] Tsai, C., Tsai, C. and Tseng, C. (2004) A New Hybrid Heuristi c Approach for Solving Large Traveling Salesman Problem. Information Sciences, 166, 67-81. http://dx.doi.org/10.1016/j.ins.2003.11.008 [22] Uğur, A. (2008) Path Planning on a Cuboid Using Genetic Algorithms. Information Sciences, 178, 3275-3287. http://dx.doi.org/10.1016/j.ins.2008.04.005 [23] Su, S.B. and Cao, X.B. (2013) Jumping PSO with Expanding Neighborhood Search for TSP on a Cuboid. Chinese Journal of Electronics , 22, 202-208. [24] Uğur, A., Korukoğlu, S., Calıskan, A., Cinsdikici, M. and Alp, A. (2009) Genetic Algorithm Ba sed Solution for Tsp on a Sphere. Mathematical and Computational Applications, 14, 219-228.
|