 Journal of Computer and Communications, 2014, 2, 77-81 Published Online March 2014 in SciRes. http://www.scirp.org/journal/jcc http://dx.doi.org/10.4236/jcc.2014.24011 How to cite this paper: Hyun, D.-K. and Lee, H.-K. (2014) A Low-Complexity Mobile Watermarking Scheme Resisting Scale Distortions. Journal of Computer and Communications, 2, 77-81. http://dx.doi.org/10. 4236/j cc.2014. 24011 A Low-Complexity Mobile Watermarking Scheme Resisting Scale Distortions Dai-Kyung Hyun, Heung-Kyu Lee* Department of Computer Science, Korea Advanced Institute of Science and Technology, Daejeon, Korea Email: *hklee@mmc.kaist.ac .kr Received Novemb er 2013 Abstract In mobile environment, a low-complexity is the significant feature because the mobile device has very limited resources due to power consumption. In this paper, we propose a low-complexity watermarking scheme for mobile device. We apply the minimum average correlation energy Mel- lin radial harmo nic (MACE -MRH) correlation filter to watermark detection. By the scale tolerance property of MACE-MRH correlation filter, the proposed watermark detector can be robust to scal- ing attacks. Empirical evidence from a large database of test images indicates outperforming per- formance of the proposed method. Keywords Low-Complexity; Mobile Watermarking; MAC E -MRH Correlation Filter 1. Introduction With the development of mobile devices, the copyright protection on mobile devices has become more impor- tant. One of the best methods for copyright protection is digital watermarking. Digital watermarking is a solu- tion to the copy protection by inserting a pattern of bits, which identifies the digital content’s copyright informa- tion, into digital content [1,2]. Digital watermarking offers persistent digital identify carried directly within con- tent. Thus, in the mobile environment, it can be easily applied. In real-world watermarking scenario, the watermark should be robust to scaling attacks because digital con- tents can be easily scaled. Many watermarking methods resilient to geometric distortion such as scaling were reported. Pereira and Pun proposed an approach to embed a digital watermark into an image using the Fourier transform [3]. This approach efficiently recovered the template in an image which has undergone a general af- fine transformation. In [4], Fourier-Mellin transform based approach was proposed. Their method utilizes g eo- metric invariant property of Fourier-Mellin transform. The method was unaffected by any combination of rota- tion, scale and translation transformations. Alghoniemy and Tewfik presented a watermarking scheme based on its moments. The watermark was composed of the mean of several functions of the second and third order scal- ing invariant moments. Their method was to be robust to geometric manipulations [5]. In mobile environment, one of the significant features is low complexity because the mobile device has very *  D.-K. Hyun, H.-K. Lee limited resources due to power consumption. Thus, the watermarking method should have a low-complexity. However, the previous works require complicated calculations such as wavelet transform and Fourier-Mellin transform in the process of watermark embedding and extracting. Therefore, we propose a low-complexity wa- termarking method to be robust scaling attacks. To be robust to scaling distortion, we adopt the minimum average correlation energy Mellin radial harmonic (MACE-MRH) correlation filter to watermark detection. The MACE-MRH correlation filter allows specifying the scaling response of the correlation filter. Thus, this filter has the scaling tolerance property. It is required a complicated computation to generate the MACE-MRH correlation filter. However, it can be designed off-line and needs only one generation of the filter during the watermark detection. Once the filter is generated, it only requires a calculation of cross correlation. Therefore, the proposed method has very low complexity. The rest of this paper is organized as follows. In Section 2, we describe the MACE-MRH correlation filter. Our watermarking scheme is presented in Section 3. Experimental results are shown in Section 4 and Section 5 which concludes the paper. 2. MACE-MRH Correlation Filter [6] In this section, we describe MACE-MRH correlation filter design theory. The MACE-MRH correlation filter is based on the Mellin radial harmonic (MRH) transform, given by the following pair of equations: 21 1 21 (,) () where( )(,) jm m m Rjm md MM M LMd π π ρφ φρ φρφρρ ρ ∞− =−∞ − −− = = ∑ ∫ (1) where M(ρ,φ) is the FT of a 2-D pattern m(x, y) in polar coordinates and Mm(φ) is the m-th MRH function of M(ρ,φ). The scale invariance property of the MRH transform is explained as follows. If gβ(x, y) is a scaled version of 2-D pattern g(x, y), i.e., gβ(x, y) = g(βx, βy), then the m-th MRH function of the 2-D polar FT of gβ(x, y) is given by 1 21 () () jm mm GL G π β φβ φ −− − = (2) where Gm(φ) is the m-th MRH function of the 2-D polar FT of g(x,y). Thus, the scaling operation only affects the MRH transform coefficient functions by a phase factor β−j2πm−1. If the 2-D polar FT of the reference pattern and the correlation filter in polar coordinates are represented as F and H, respectively, we obtain the following expression for the correlation value c between F(ρ,φ) and H(ρ,φ). 2* 0 (,) (,). R d cF Hdd π ρφρφρρ φ = ∫∫ (3) If L = ln(R/d) in Equation (1) is an integer, the MRH components are orthogonal. Equation (3) can be de- composed in terms of MRH decompositions in Equation (1). 2* 0 ,()() . mmm m m cL CCF Hd π φ φφ ∞ =−∞ = = ∑∫ (4) Supposing a scaled pattern fβ(x, y) = f(βx, βy), we can rewrite Equation (4) by the scale invariance property of Equation (2) as a function of the scale factor β: 12 ln () . jm m m c eC πβ ββ ∞ −− =−∞ = ∑ (5) Equation (5) can be simplified by a invertible logarithmic transformation Λ so that we yield c(β) in Equation (6) () 22 ˆ(){()}( ). LL j Lm m m cce ceCe ββ β ππ ββ ∞− =−∞ =∧=⋅= ∑ (6) The relationship between the transformed scale response c(β) and the coefficients Cm is exactly the same as 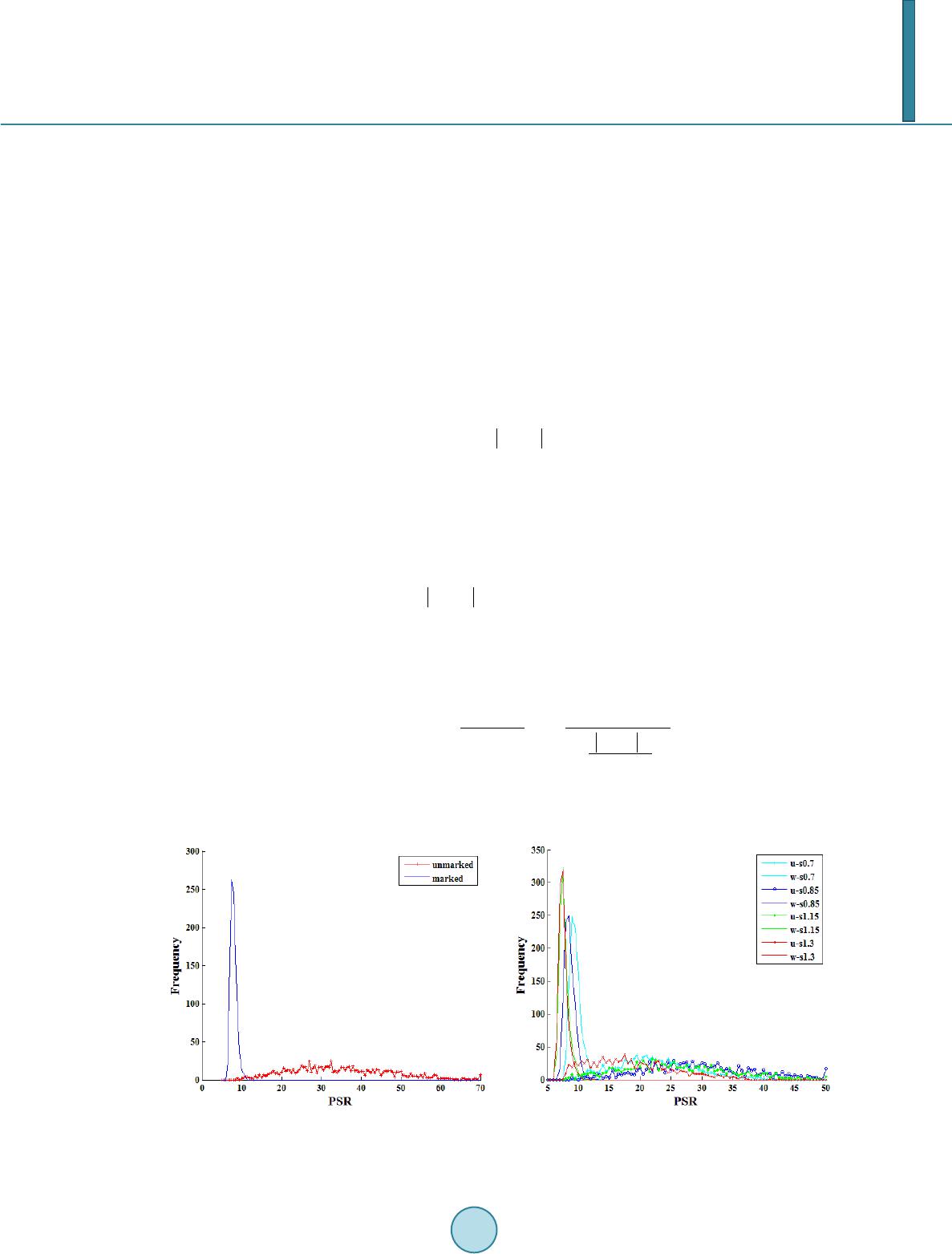 D.-K. Hyun, H.-K. Lee A(w) and ak of Equ ation (6), which represent the frequency response of the finite impulse response (FIR) filter and the k-th coefficient of the impulse response, respectively. ( 7) The similarity of Equation (6) and Equation (7) can make the problem of calculating MRH weighting values Cm as that of designing the FIR filter of . Thus, by employing available a FIR filter design algorithm [7], we can calculate the weighting values Cm of c(β). Once the Cm are determined, they can be used as constraints for determining MRH function Hm(φ) of Equa- tion (5). However, for each m, there are many Hm(φ) candidates that satisfy the constraints. Thus, more con- straints are needed to find a unique solution. Therefore, we select Hm(φ) that minimize the average correlation energy (ACE) while satisfying the relationship in Equation (5), thereby maximizing the sharpness of output peak while achieving a specified scale response c(β). The ACE is equal to the average energy of the correlation filter as described in Equation (8). 22 0 () () mF m ACE LHPd π φ φφ ∞ =−∞ = ∑∫ (8) where PF(φ) is the average power spectrum of the reference pattern obtained by computing the average of F(ρ, φ)2 along the radial axis.The MACE-MRH correlation filter is designed to minimize the ACE in Equation (8) while satisfying the relationship in Equa tion (5). Thus, the filter H(u, v) can be obtained by solving the follow- ing minimization problem. 22 0 2* 0 Find( )tominimize () () subject to () () m mF mm m H H Pd FH dC π π φ φ φφ φ φφ = ∫ ∫ (9) Using the method of Lagrange multipliers, the solution to the minimization problem of Equation (9) is * 2 2 0 () () () , () () () mm mm m Fm F FF HPFd P π φφ φλ λ φα φφ φα = = + + ∫ (10) where α is a small additive constant. Finally, the correlation filter H(u, v) is found by applying the inverse MRH transforms of Hm(φ) and applying a polar-to-cartesian coordinate transform. (a) (b) Figure 1. Empirical detector performance: (a) Before scaling; (b) After scaling.  D.-K. Hyun, H.-K. Lee 3. Proposed Method The previous section described how a MACE-MRH correlation filter was designed. In this section, it is ex- plained how the MACE-MRH correlation filter is applied to the proposed watermark detection. 3.1. Watermarking Embedding We propose a simple additive watermarking method for low-complexity. First, a simple perceptual marking ma- trix M is calculated as below: 111 ,18 1 111 M FIF −−− =∗=− − −−− (11) where I is a sample image. After that, the watermarked image Y is computed as follows: (12) where W is a white watermark. The embedding process has very low-complexity. Therefore, it can be suitably applied on the mobile envi- ronment. 3.2. Watermark Detection To be robust to scaling attacks, we adopt the MACE-MRH correlation filter designed from watermark pattern W of Equation (12). We design MACE-MRH correlation filter from watermark pattern be determining the scale response c(β) as follows: 0 1, ( ,()),()0, t if Hf Wccotherwise ββ ββ ≤ == (13) where f0 is the filter design function of Equation (10). This procedure would be required a complicated compu- tation. However, it needs only one generation of the filter during the watermark detection. After generating MACE-MRH correlation filter, the proposed method requires only a computation of cross- correlation as follow: 00 filter filter (, )( ,)(,) where(),( ) MN mn ccxyHm nWmx ny HfHWIfI = = =⋅ ++ == − ∑∑ (14 ) From the correlation result, the proposed method determined whether watermark was embedded or not as fol- low: peak peak (,) mean() Watermark wasembedded:, Watermark was not embedded:standard deviation() cc ijcc PSR PSR PSR cc τ τ − ≥= < (15) where (ipeak,jpeak) are the peak position in cc(x, y) and τ is threshold. 4. Experimental Results The experiment was performed with 1000 watermarked images with β = 0.5. To demonstrate the performance about scaling attacks, the images were resized in increments of 0.15 from 0.7 to 1.3. With the watermarked im- ages, we measured the resulting correlation performances in term of peak to side robe ratio (PSR) of Equation (15). Figure 1 shows the PSR histogram of un-scaled image and scaled image. It shows that the proposed me- thod is robust to scaling attacks. We also calculate the average detection rate by determined threshold τ of Equation (15) to false positive rate (FPR) = 10−3. Table 1 shows the average detection rate on FPR = 10−3. The experimental result indicates that the proposed method maintains high performance with scaled images.  D.-K. Hyun, H.-K. Lee Table 1. Detection rate (%) at FPR = 10−3. Scaling factor Detection rate (%) 0.7 94.6 0.85 97.9 1 98.2 1.15 93.6 1.3 92.7 5. Conclusion In this paper, we introduced a low-complexity mobile watermarking scheme. By applying MACE-MRH correla- tion filter to a simple additive watermarking, our method has very low-complexity and is robust to scaling at- tacks. The experimental results show that the proposed method can be detected watermark from scaled images. Acknowledgements This work was partially supported by Defense Acquisition Program Administration and Agency for Defense Development under the contract (UD060048AD). References [1] Cox, I.J. and Miller, M.L. (2001) Electronic Watermarking: The First 50 Yea rs. Proceedings of IEEE International Workshop on Multimedia Signal Processing, 225-230. [2] Hartung, F. and Kutter, M. (1999) Multimedia Watermarking Technique. Proceedings of IEEE, 87, 1079-1107. http://dx.doi.org/10.1109/5.771066 [3] Pereira, S. and Pun, T. (2000) Robust Template Matching for Affine Resistant Image Watermarks. IEEE Transactions on Image Processing, 9, 1123-1129. http://dx.doi.org/10.1109/83.846253 [4] O’Ruanaidh, J.J.K. and Pun, T. (1998) Rotation, Scale, and Translation Invariant Spreadspectrum Digital Image Wa- termarking. Signal Processing, 66, 303-317. http://dx.doi.org/10.1016/S0165-1684(98)00012-7 [5] Alghoniemy, M. and Tewfik, A.H. (2000) Image watermarking by moment invariant. IEEE International Conference on Image Processing, 73-76. [6] Kerekes, J. R. a nd Kumar, B. (2006) Correlation Filters with Controlled Scale Response. IEEE Transactions on Image Processing, 15, 1794-1802. http://dx.doi.org/10.1109/TIP.2006.873468 [7] Oppenheim, A.V. and Schafer, R.W. (1975) Discrete-Time Signal Processing. Prentice-Hall, Englewood Cliffs.
|