Journal of Computer and Communications, 2014, 2, 58-65
Published Online March 2014 in SciRes. http://www.scirp.org/journal/jcc
http://dx.doi.org/10.4236/jcc.2014.24009
How to cite this paper: Hou, J.-U., Ji, S.-K. and Lee, H.-K. (2014) Fast Watermark Synchronization Based on Complementary
Templates. Journal of Computer and Communications, 2, 58-65. http://dx. doi.org/10. 4236/j cc.201 4.24009
Fast Watermark Synchronization Based on
Complementary Templates
Jong-Uk Hou1, Sang-Keun Ji2, Heung-Kyu Lee1*
1Division of Web Science and Technology, Korea Advanced Institute of Science and Technology (KAIST),
Daejeon, South Korea
2Department of Computer Science, Korea Advanced Institute of Science and Technology (KAIST), Daejeon,
South Korea
Received Novemb er 2013
Abstract
A recent trend of the digital watermark requires not only the robustness but also speed. To achi-
eve these requirements, we propose a watermark synchronization scheme based on two kinds of
templates. The first one is the rotation invariant template for estimating scale parameter, and the
second is the scale invariant template for estimating rotation parameter. Theoretically, comple-
mentary templates greatly reduce the search space at the detection stage and achieve robustness
against the RST distortion. The results report that the proposed method is useful for the water-
mark detection system which requires both a real-time detection and robustness.
Keywords
Digital Image Watermarking; Template Matching; Affine Transform; Real-Time Detection
1. Introduction
In the age of the Internet, digital contents have become one of the most popular information sources. Because
the Internet is an excellent distribution system for digital contents, copyright protection of digital contents is re-
quired. Digital watermarking is one of the most popular technologies for the copyright protection of digital con-
tents such as images, videos, and audio.
The digital watermark is a code that can be embedded in various forms of digital content, but is generally in-
visible to people. However it is detectable by electronic devices such as computers, networks, and mobile de-
vices. Digital watermarks applied to digital contents are persistent, staying with the content through copying,
manipulation, and so on. Traditionally, the watermark is used for copyright protection of published contents. But
a recent trend of the digital watermark not only protects the published contents but also used for enhancing the
user’s experience [1].
The aspects of user experience, the watermarks can be applied in many directions, especially the mobile de-
vice environment. For example, Digimarc discovery [2] uses the image watermark in printed advertisements to
*
Corresponding author.

J.-U. Hou et al.
59
provide a uniform resource locator (URL) of additional resources.
In order to enable these kinds of services, the watermark is easily detected and extracted by a mobile device.
However, the detection of the watermark through the mobile devices is much harder due to their relatively low
hardware performance. Moreover, the capturing environments are diverse because of the unsteady holding of the
device, and a variety of camera resolutions. Therefore, the detection process must require less computation
power and be robust against various kinds of distortions, especially the rotation, scale, and translation (RST).
To cope with these kinds of difficulties, we propose an efficient watermarking synchronization method based
on the two kinds of templates. The first one is the rotation invariant template for estimating scale parameter, and
the other is the scale invariant template for estimating rotation parameter. Theoretically, complementary tem-
plates greatly reduce the search space at the detection stage and achieve robustness against the RST distortion.
The rest of this paper is organized as follows. Section 2 explains problems of previous works in watermark
detection by mobile device. In Section 3, we define the complementary templates and describe a theoretical
analysis of them. And we present our test environments and results in Section 4.
2. Problems of Previous Works
To cope with difficulties in watermark detection with RST distortions, various schemes have been proposed.
These methods use the discrete Fourier transform (DFT) to achieve robustness against rotation and scaling. The
DFT based methods can be divided into two categories, one is based on the invariance [3-5], and another is
based on template matching [6,7].
The invariance based watermarking using the log-polar-mapping (LPM) scheme is theoretically perfect for
the RST distortions. However, most of these algorithms are difficult to implement, because the LPM and the in-
verse LPM distort the embedded watermark. The template matching based algorithms are relatively easy to im-
plement and have good performance for various geometric distortions. However, in order to estimate the dis-
torted parameter using a template, most of those algorithms consume much computation resource. Because of
their complexity of computation, those algorithms are not suitable for mobile application s.
3. Proposed Method
We propose an efficient watermarking synchronization method based on the two kinds of templates. The tem-
plates contain no information but are only an indicator to recover possible transformation in the image. Table 1
show the estimation parameter and invariance property of each template.
The template Tρ is rotation invariant template for estimating scale parameter, and Tθ is scale invariant tem-
plate for estimating rotation parameter. Because each template has invariance for estimating a parameter of the
other one, they complement each other. In this paper, we refer to these templates as complementary templates.
3.1. Templates Definition
As shown in Figure 1, proposed templates are embedded in a transformed domain of host image f(x1, x2) de-
fined in following Equation (1):
F(k1, k2) = F [f(x1, x2)], (1 a)
FL(kρ, kθ) = L [F(k1, k2)], (1b)
Iρ(ξρ, kθ) = F [FL(kρ)], (1c)
Iθ(kρ, ξθ) = F [FL(kθ)]. (1d)
Table 1. Functions of the templates.
ID Estimation parameter Invariance
Tρ scale (ρ) rotation
Tθ rotation (θ) scale

J.-U. Hou et al.
60
I
ρ
(ξ
ρ
, k
θ
)
T
θ
T
ρ
I
θ
(k
ρ
, ξ
θ
)
F
M
(k
ρ
, k
θ
)
F(k
1
, k
2
)
f(x
1
, x
2
)
kρ
kθ
Figure 1. Diagram for the proposed templates.
where
F [·] and L [·] are computation operator for the discrete Fourier transform (DFT) and Log-polar mapping
(LPM) respectively. The complementary templates are defined as magnitude points in Iρ(ξρ, kθ) and Iθ(kρ, ξθ)
domains as following Equation (2):
Tθ: (tρ, cθ) ∈ Iρ(ξρ, kθ) (2 a )
Tρ: (cρ, tθ) ∈ Iθ(kρ, ξθ) (2 b )
where tρ, tθ are the values for the position of templates and cρ, cθ are constant values. The tρ and tθ are used for
the rotation and scale estimation parameters respectively. Iρ(tρ, cθ) and Iθ(cρ, tθ), the intensity of templates, shall
be larger than a threshold value τρ and τθ adaptively determined in embedding process.
3.2. Properties of Templates
Using the definition in the previous section, we can briefly describe the properties of the proposed templates. As
describe in Equation (1a), the proposed templates inherited the properties of DFT. The magnitude of the DFT is
invariant to translation in spatial domain as shown in the Equation (3):
F(k1, k2) exp[−j(ak1+bk2)] ↔ f(x1+a, x2+b). (3)
Spatial shifts affect only the phase representation of an image. ConsEquationuently, proposed templates ob-
tain circular translation invariance in spatial domain.
The Equation (1b) shows the LPM of the DFT magnitudes. The LPM operation generates the 2-dimensional
coordinate system FL for scaling and rotation parameter [8]. If FL is transformed by 1-dimensional DFT in the
direction of kθ, transformed domain Iθ for rotation parameter obtains shift invariance.
Therefore, the Tρ is independent for an image rotation, and it is proper to estimate the scaling parameter. Si-
milarly, the Tθ is independent for an image scaling, and it is suitable to estimate the rotation parameter.
3.3. Embedding Process
Templates are embedded in following steps:
1) Determine position of templates tρ and tθ in transformed domain Iρ and Iθ.
2) Determine the strength of the Tρ, Tθ adaptively.
3) Calculate F(k1, k2) domain magnitude from Iρ(tρ, cθ) and Iθ(cρ, tθ).
4) Add result of step 3) to the DFT magnitude of the original (or watermarked) image.
5) Apply inverse DFT to result of step 4) and get the template embedded image.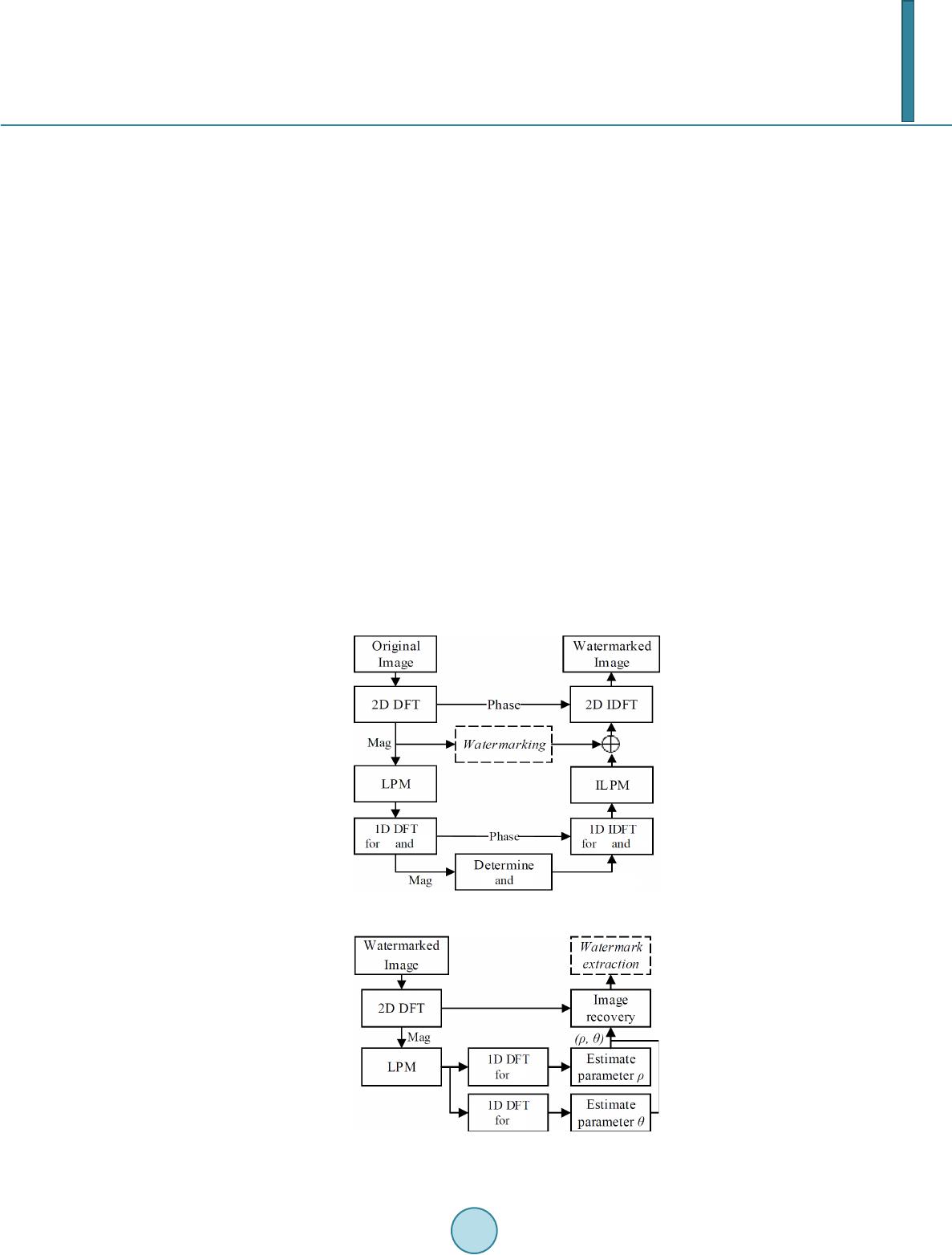

J.-U. Hou et al.
61
3.4. Detection Process
Templates are detected in following steps:
1) Apply 2-D DFT to the watermarked image.
2) Apply LPM to magnitude obtained in step 1).
3) Apply 1-D DFT to the direction of radius (kρ) and angle (kθ) to get Iρ, Iθ domain.
4) Find Tρ in Iρ domain for constant cθ as following Equation (4 ) and determine the scaling parameter. If
Iρ(
ˆ ρ
, cθ) < τρ then the system decided that Tθ is not detected.
()
ˆarg max, Ic
ρ
ρ ρθ
ξ
ρξ

=
(4)
5) Find Tθ in Iθ domain for constant cθ as following Equatio n (5) and determine the rotation parameter. If Iθ(cρ,
ˆ
θ
) < τθ then the system decided that Tρ is not detected.
( )
ˆarg max,Ic
θ
θ ρθ
ξ
θξ

=
(5)
6) (Optional) Recover the transformed image using estimated parameters
ˆ ρ
and
ˆ
θ
. The operator S (ρ)[·]
and R(θ)[·] denote the rotation and scaling transformation for their input parameter.
F`(k1, k2) = S
−1(ρ)·R−1(θ)·F(k1, k2) (6)
7) Extract watermark using the result of detection process.
We note that the flat-top window [9] is applied in before the DFT calculation to reduce the leakage.
3.5. Time Complexity of the Detection Process
Due to the improvement of hardware, FFT on the mobile device is no longer treated as a time consuming
k
θ
k
ρ
k
θ
k
ρ
T
θ
(t
ρ
, c
θ
), (c
ρ
, t
θ
)
T
ρ
Figure 2. Embedding process.
kθ
kρ
Figure 3. Detection process.

J.-U. Hou et al.
62
computation [10]. And depending on its implement, LPM can be computed in a constant time. Therefore, to
show the usefulness of a proposed method, we analyze the complexity of the template searching step.
As shown in Figure 4(a), computation complexity of previous approach for rotation and scaling template
searching is O(ρ·θ) = O(n2), since the template is dependent to both rotation and scaling parameters. On the oth-
er hand, as shown in Figure 4(b), a computation complexity of a proposed method is O(ρ) + O(θ) = O(n). Be-
cause each complementary template has invariance for estimating a parameter of the other. For example, the
system searches only Iρ domain for a constant cθ to detect Tρ, because of a rotation invariance of Iρ and Tρ. In this
way, complementary templates greatly reduce the search space at template detection stage.
3.6. Watermark System for a Proposed Method
As mentioned in the beginning part of this section, there is no information in the complementary templates. The
templates only provide an invariant domain for a watermarking algorithm. In order to build an actual water-
marking system, a proper watermarking algorithm should be prepared.
The required watermarking algorithm has to have a shift invariance property for spatial domain, since the
templates cannot recover the translation of the original image. The watermarking algorithm also requires fast
and simple computation to utilize the contribution of complementary templates the fast estimation. Therefore,
simple DFT based watermarking algorithms [11,12] are suitable for the proposed domain.
In addition, if a mobile device provides a streaming capturing process such as viewfinder mode, we can im-
prove a performance of proposed domain. The signal of watermarks in proposed domain is cumulative, since the
proposed domain is invariant for RST distortion.
4. Results
4.1. Experimental Setup
In order to obtain a robust system, several parameters of our algorithm have to be carefully set. We have found
experimentally that normalized frequencies for cρ and cθ are 0.44 and 0.60, respectively. In order to make tem-
plates invisible, all parameters are set to yield a PSNR no greater than 35 dB. The thresholds τρ and τθ are set so
that false positive rates are minimized. We use the image of Len a to test proposed method. In order to test the
robustness of the proposed schemes, the tests consisted of the combination of attacks: rotation, and scaling.
With the above setup, a machine consisting of Intel i7-3770 (3.40 GHz) with 16 GB main memory is used to
measure the detection performance. Matlab R2012b environment is used to implement and execute our algo-
rithm.
4.2. Template Detection Result
Figure 5 shows the sample template embedded images and the transformed domain of (a) and (b). To make the
Figure 5(d), template embedded image is resized by 1.2 and rotated by 30˚.
The complementary templates are shown as small white dots in the transformed domain highlighted 10 times
brighter. The properties of template are observed in Figure 5. For example, vertical positions of the peaks in
Figure 5(e) are not changed after the scaling. Similarly, horizontal positions of the peaks in Figure 5(f) are not
changed after the rotation.
(a) (b)
Figure 4. Geometric interpretation of search space for scaling and
rotation parameter. (a) Previous methods; (b) Proposed methods.

J.-U. Hou et al.
63
(a) (b)
(c) (d)
(e) (f)
Figure 5. (a) is a template embedded image, (d) is a distorted version of (a), and
transformed domain of (a) and (d). Templates are shown as small white dots. (c) Iρ
domain of (a); (d) Iρ domain of (b); (e) Iθ domain of (a); (f) Iθ domain of (b).
Figure 6 reports the detection accuracy of the complementary templates for the rotation and scaling. The re-
sults report that the proposed method provides the robustness to the scaling, rotation, and combination of both
transforms.
4.3. Time Consumption Result
In the template detection stage, the proposed method takes a total of 107 milliseconds to estimate rotation and
scaling parameters. 85 milliseconds are consumed for computing Iρ and Iθ domains, and only 1 millisecond is
spent on finding the templates. We should note that most of the computation occurred in the Log-polar mapping
which consists of several resampling processes. If the Log-polar mapping process is optimized for time con-
sumption, we can greatly reduce the whole computation time.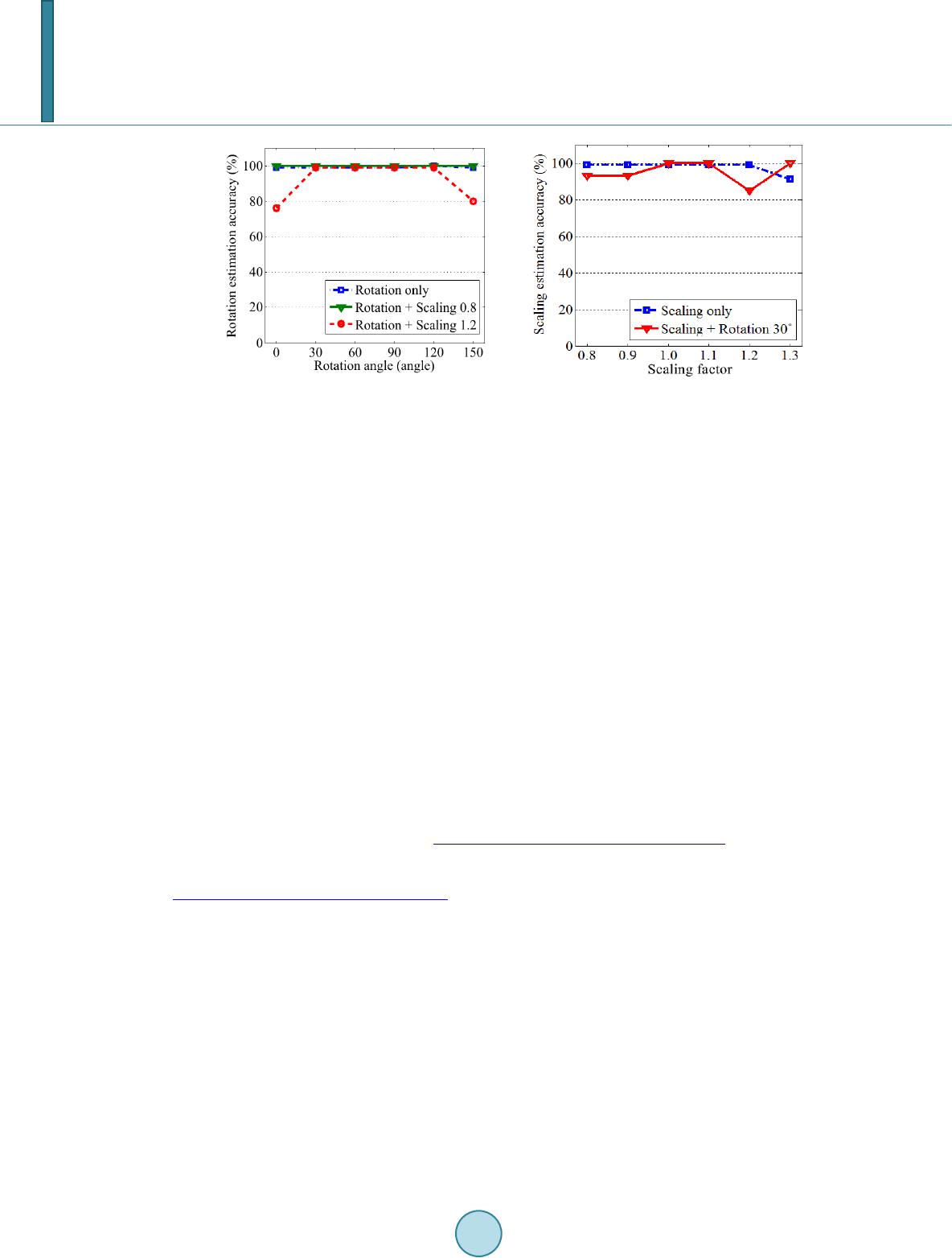

J.-U. Hou et al.
64
(a) (b)
Figure 6. Robustness to (a) Rotation; (b) Scaling.
5. Conclusions
The main contribution of the complementary templates is a real-time estimation of scaling and rotation parame-
ters. Therefore, the watermark detection algorithms with our methods no more require robustness for the rotation
and scaling distortion. It allows the design of a watermark detection algorithm that concentrates on only a detec-
tion speed. Especially, it is useful as a watermark detection system for mobile devices that require both real-time
detection and robustness.
However, our proposed method is not perfectly protected against other geometric distortions such as shearing
and projection. Therefore, our future work will concentrate on coping with other geometric distortions. We also
plan to design a proper watermarking algorithm for our proposed domain.
Acknowledgements
This research was supported by a grant from the Advance Technology Center R&D Program funded by the
Ministry of Trade, Industry & Energy of Korea (10042252).
References
[1] Digital Watermarking Alliance. Enabling New Mobile Applications—A Comparison of Technologies.
[2] Rodriguez, T.F. and Bavi s, B.L. (2012) Channelized Audio Watermarks. US Patent US 2012/0277893.
[3] Ruanaidh, J.J.K.O. and Pun, T. (1998) Rotation, Scale and Translation Invariant Spread Spectrum Digital Image Wa-
termarking. Signal Processing, 66, 303-317. http://dx.doi.org/10.1016/S0165-1684(98)00012-7
[4] Zheng, D., Zhao, J.Y. and Saddik, A.E. (2003) RST-Invariant Digital Image Watermarking Based on Log-Polar Map-
ping and Phase Correlation. IEEE Transactions on Circuits and Systems for Video Technology, 13, 753-765.
http://dx.doi.org/10.1109/TCSVT.2003.815959
[5] Xu, X., Zhang, R. and Niu, X.X. (2010) Image Synchronization Using Watermark as R ST Invariant Descriptors. 2010
IEEE International Conference on Information Theory and Information Security (ICITIS), 831-836.
[6] Pereira, S. and Pun, T. (2000) Robust Template Matching for Affine Resistant Image Watermarks. IEEE Transactions
on Image Processing, 9, 1123-1129.
[7] Kang, X.G., Huang, J.W., Shi, Y.Q. and Lin, Y. (2003) A DWT-DFT Composite Watermarking Scheme Robust to
Both Affine Transform and JPEG Compression. IEEE Transactions on Circuits and Systems for Video Technology, 13,
776-786.
[8] Araujo, H. and Dias, J.M. (1996) An Introduction to the Log-Polar Mapping [Image Sampling]. Proceedings of Second
Workshop on Cybernetic Vision, 139-144.
[9] Ramirez, R.W. (1985) The FFT: Fundamentals and Concepts. Prentice-Hall, Englewood Cliffs.
[10] Johnson, S.G. and Frigo, M. Benchfft: A Program to Benchmark FFT Software.
[11] Solanki, K., Dabeer, O., Madh ow, U. , Manjunath, B.S. and Chandrasekaran, S. (2003) Robust Image-Adaptive Data
Hiding: Modeling, Source Coding, and Channel Coding. 41st Allerton Conference on Communications, Control, and

J.-U. Hou et al.
65
Computing.
[12] Rosa, A., Barni, M., Bartolini, F., Cappellini, V. and Piva, A. (2000) Optimum Decoding of Non-Additive Full Frame
dft Wa termark s. In: Pfitzma nn, A., Ed., Information Hiding, Lecture Notes in Computer Science, Vol. 1768, Springer,
Berlin, Heidel berg, 159-171.