 Journal of Computer and Communications, 2014, 2, 31-38 Published Online March 2014 in SciRes. http://www.scirp.org/journal/jcc http://dx.doi.org/10.4236/jcc.2014.24005 How to cite this paper: He, W.Q. and Peng, X. (2014) Identity Authentication Based on Two-Beam Interference. Journal of Computer and Communications, 2, 31-38. http://dx.doi.org/10.4236/jcc.2014.24005 Identity Authentication Based on Two-Beam Interference Wenqi He, Xiang Peng* College of Optoelectronic Engineering, Key Laboratory of Optoelectronics Devices and Systems, Education Ministry of China, Shenzhen University, Shenzhen, China Email: *xpeng@szu.edu.cn Received October 2013 Abstract A two-factor identity authentication method on the basis of two-beam interference was presented. While verifying a user’s identity, a specific “phase key” as well as a corresponding “phase lock” are both mandatory required for a successful authentication. Note that this scheme can not only check the legality of the users, but also verify their identity levels so as to grant them hierarchical access permissions to various resources of the protected systems or organizations. The authentication process is straightforward and could be implemented by a hybrid optic-electrical system. However, the system designing procedure involves an iterative Modified Phase Retrieval Algorithm (MPRA) and can only be achieved by digital means. Theoretical analysis and simulations both validate the effectiveness of our method. Keywords Optical Information Security; Optical Aut hen ti cat i on; Two-Beam Interference 1. Introduction In the past decade, the theories and technologies of information security with optical means have drawn a lot of attentions due to its inherent advantages such as the ability of parallel data processing and the designing freedom of multiple-dimension. The most famous and important work in this area must be the image encryption scheme based on Double Random Phase Encoding (DRPE), which is reported by Refregier and Javidi in 1995 [1]. Up to now, plenty of relevant works have been studied and developed, and they mainly concentrate on the aspects of image encryption/hiding and optical cryptanalysis [2-15]. In a recent letter, Zhang et al. proposed an approach for image encryption based on two beams’ interference, in which an image was separated into two Phase-Only Masks (POMs) through an analytical derivation [16]. Soon after, they again developed a method for hiding two images by introducing an extra phase retrieval algo- rithm [17]; Zhu et al. employed a polarization-selective Diffractive Optical Element to generate a desired secret image based on interference between two polarized wave fronts [18]; Han et al. proposed an alternative way to encode a secret image into a POM and an Amplitude-Only Mask relying on the principles of interference and vectors addition [19]; Tay et al. further applied the encryption scheme to encrypt color images [20]; More re- *  W. Q. He, X. Peng cently, Kumar et al. and Weng et al. independently showed the experimental results to verify the effectiveness of the optical image encryption based on interference [21,22]; Yang et al. introduced the concept of stream ci- pher to encode the secret images into two POMs based on Michelson interferometer, in which one POM is served as the encryption key while the other regarded as the ciphertext [23]; Yuan et al. and He et al. reported two kinds of image hiding methods for one image and multiple images separately on the basis of two beams’ in- terference [24-26]. However, to the best of our knowledge, most of the aforementioned image encryption sch- emes are also sufficiently suitable to be explained as an authentication system. In this paper, we are going to de- scribe a two-factor identity authentication infrastructure with the help of two-beam interference and the MPRA. The rest of this paper is organized in the following sequence: In Section 2, we first give a brief introduction of the Hash function and then come to a detailed description of the user authentication process and the system de- signing process successively. In Section 3, we provide the computational simulations to validate the feasibility of our method. In Section 4, we make the concluding remarks. 2. Description of the Method When a user attempts to access to the confidential resources of the protected system, an authentication process is mandatorily required in advance. The involved steps are detailed as (Figu re 1): 1) User enters a private pass- word through an external device. By identifying the input password with all the passwords pre-stored in the da- tabase, the system can thus accomplish a preliminary verification: if there is not a match, that implies the visitor is unauthorized, and if there appears a match, a corresponding “phase lock” is then loaded and written into the Spatial Light Modulator (SLM1); 2) After the confirmation of the first step, the user is indicated to plug in his “phase key”, which is accordingly written into the SLM2; 3) Two coherent plane waves, then modulated by the SLM1 and SLM2 separately, pass through a Half Mirror (HM) together and interference with each other at the output plane leading to an output image. It is recorded by a Charge-Coupled Device (CCD) and can be mathe- matically expressed as: exp(( ,))*( ,,)exp(( ,))*( ,,)( ,)exp(( ,)) lk O jxyhxylj xyhxylOxyj xy ψψ ϕ +=⋅ , (1) where and are the distributions of the phase lock and phase key respectively, represents the pulse response function of the Fresnel diffraction on the distance , the symbol * means Figure 1. User authentication process. 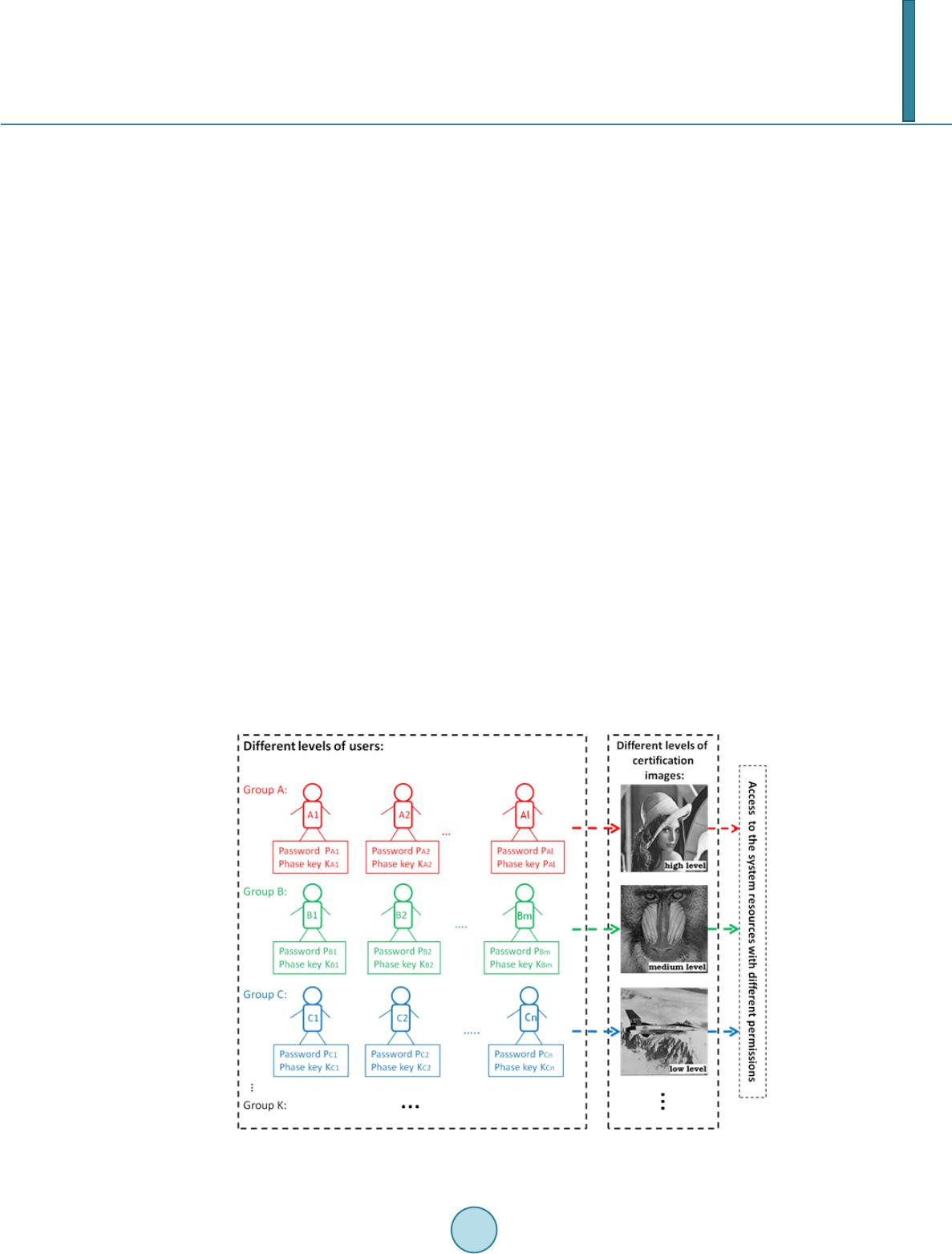 W. Q. He, X. Peng convolution operation, and are the amplitude part and phase part of the complex in- terference field at the output plane, respectively. Note that is then regarded as the output image, which is proportional to the interference intensity pattern; 4) By calculating the Correlation Coefficients (CCs) between the output image and the standard certification images in the database, one can easily allege whether the user’s visiting request is legal: If the value of CC is higher than the predetermined threshold (e.g. 0.95), it means a successful authentication while lower means a failure one. To further explain the functionary of identity authentication of the proposed scheme, we provide a schematic diagram showed as Figure 2. According to the pre-established different levels of visiting permissions, all the legal users are divided into several groups (such as Group A, Group B, Group C, …, Group K) in advance, each of which has an amount of legal users depending on the practical requirement. For example, in Group A, B, C, the number of users is “l”, “m” and “n”, respectively. And every user in all the groups is assigned a private password and a phase key for authentication. It’s worth to point out that different groups have been pre-assigned different standard certification images, and the details will be described later. That also means that the users of different groups will generate different certification images and then obtain different permissions to access to the system. As shown in Figure 2, the standard certification image “Lena” corresponds to the “high level” users, who can access all the confidential resources and have the highest priority, the image “Baboon” means the “me- dium level” users and the image “Airplane” stands for the “low level” users. Prior to the designing process of our identity authentication method, as mentioned previously, we need first classify all the legal users into several groups with different permissions according to the actual requirements. Meanwhile, we also need to assign the standard certification images (e.g. the image “Lena”, “Baboon”…) for each group. Here, we would like to roughly introduce the designing procedure by taking the “Group C”, men- tioned in Figure 2, as an example, and it can be depicted as follows: 1) Select a set of passwords arbitrarily (PC1, PC2, …, PCn); 2) For each user of the Group C (e.g. user C1), we create a phase lock (LC1) with the help of a pseudo random number generator, where the user’s password is entered as the seed. Thereafter, all the created phase locks and their corresponding passwords are linked up separately and pre-stored in the database of the system; 3) Once obtain all the phase locks (LC1, LC2, LC3, …, LCn) and given the standard certification image (“Airplane”), can we then determine all the corresponding phase keys separately by adopting MPRA technique. Up to now, we have got a sense of the designing process for Group C. And the passwords together with the phase keys are assigned to the users of Group C, separately. In the following, we would like to give a detailed description about the key technique of our scheme, say Figure 2. Function diagram of the identity authentication for various users.  W. Q. He, X. Peng MPRA as mentioned above. The problem to be solved can be described as: Give one amplitude constraint (a specific standard certification image) at the output plane, the other amplitude constraint (a matrix with all unities) at the SLM2 and a fixed shifting vector (the Fresnel diffraction of a phase lock). We need then determine the distribution of the phase key at the SLM2. To facilitate the following statement, we express the Equation (1) in another way as: (, )(, )exp((,))(, )exp((, )) KO Lxy KxyjxyOxyjxy ϕϕ +=⋅ , (2 ) where and are the Fresnel diffractions of the phase lock and the phase key , respectively. Operating a Fourier transform on both sides of Equation (2) fol- lowed by a simple derivation, we have 1 F{ (, )exp((,))(, )} exp((,))F{} F{(,,)} O k Oxyj xyLxy j xyhxyl ϕ ψ − ⋅− = , (3) where and represent the operations of Fourier transform (FT) and inverse FT, respectively. After a simple reasoning, we can realize that the system designing issue has turned to be finding a phase distribution to satisfy the Equation (3). And this issue could be further transferred as a double-constraints phase retrieval problem with a fixed vector shifting ( ). Exactly for this purpose, we developed a MPRA tech- nique. Note that this is an iterative evaluating method for seeking the optimal solution and has no analytic solu- tions. Therefore, our purpose is trying to determine the distribution of the phase key, , rendering the resultant interference pattern ( ) pretty close to the assigned standard certification image ( ), which is also be named as a target image in our MPRA. Here, the Correlation Coefficient (CC), defined as Equa- tion (4), is recommended as the criteria to evaluate the similarity of and : 22 ((,)(, ))((, )(, )) CC ((,)(, ))((, )(, )) OxyOxyOxyO xy OxyOxyO xyO xy ′′ −− =′′ −− ∑∑ ∑∑ ∑∑ (4) Now, assume that the iterative algorithm has reached the m-th loop, the succeeding iterations can be then ma- thematically expressed as: () ()() exp() exp() mm m KO KjOj L ϕϕ = − , (5a) ()1 ()() exp()Phase{F{F{exp()} F{( ,,)}}} m mm kK jK jhxyl ψϕ − = , (5b) ( 1)( 1)() exp()exp()(,,) mm m Kk Kjj hxyl ϕψ ++ = ∗ , (5 c) ( 1)(1)( 1)( 1) exp( )exp( ) mmmm OK Oj KjL ϕϕ ++++ ′= + , (5d) where the superscript notation “(m)” is the iteration times and the operator represents taking the phase from a complex amplitude. The flowchart of the whole iterative algorithm is illustrated in Figure 3 and can also be summarized as follows: 1) Calculate the Fresnel diffraction of the phase key with initialized para- meters in accordance with the Equation (5a); 2) Acquire the first estimate of the phase key by performing the inverse FT on the result of step (1) according to Equation (5b); 3) The estimated phase key propagates in Fresnel domain resulting in based on Equation (5c); 4) Construct the interference field ( ) on the output plane by adding a fixed shifting vector on the result of step (3) in line with Equation (5d); 5) Take the modulus of the outcome of step (4), it is compared with the standard certification image , if the difference is less than a predefined threshold, we stop the iteration process. Otherwise, substi- tute for and repeat the above steps. Whenever is sufficiently close to , we claim that the corresponding estimated phase key is what we are looking for. In this way, we complete the itera- tive MPRA and determine the phase key on the basis of a given standard certification image and a password- controlled phase lock. 3. Numerical Simulations We demonstrate our method with numerical simulations in the MATLAB R2010a environment. The standard  W. Q. He, X. Peng certification images employed in the following simulations are all in the size of 256 × 256 pixels and quantified to 8 bits. And the quantification issue of the phase distributions is not taken into account for simplicity. The pix- el size and the wavelength of the illuminating light are set as 0.02 mm and 632 nm respectively. Suppose that we are going to authorize three users as the members of group C mentioned above. First, we choose three passwords (“szu123”, “sdu231” and “ao312”), which are used to control the phase locks. Meanwhile, three noise-like phase locks, showed as Figures 4(a)-(c) , are constructed based on the three sets of pseudo random numbers, which are generated by a password-controlled pseudo random number generator. Third, the MPRA is applied to determine three corresponding phase keys to complete the system designing procedure. The related results are shown in Figure 4. Note that the value of threshold for CC in our whole simulations is set as 0.95. For further validation, we extend the aforementioned example to a hierarchical authentication situation with six users: one with high level permission, two with medium level permissions and three with low level permissions. Figure 3. Flowchart of the MPRA. Figure 4. (a)-(c) Three constructed phase locks; (d)-(f) Three corresponding output images, the CCs between them and the standard certification image (“Airplane”) are 0.9586, 0.9565 and 0.9573, separately; (g)-(i) The distribu- tions of corresponding phase keys.  W. Q. He, X. Peng The results are shown in Figure 5 and depicted in Table 1. It should be noticed that a phase key together with each unmatched phase locks can also lead to an output image, which is similar with the standard certification image by naked eyes. This implies a potential security leak in practical applications. However, the data provided by Table 1 tell us a fact that it will not happen because the CC values between the incorrect output images and the standard certification image are far lower than the pre-selected threshold. 4. Conclusion We presented a two-factor identity authentication scheme based on two-beam interference principle. A two beams’ interferometer is adopted as the main unit to accomplish the authentication, and a MPRA technique is developed to determine the phase keys for the authorized users. Compared with some common authentication systems, the main advantages of our proposed method are that we cannot only check whether the user is legal but also verify its identity level. Furthermore, the two-factor (password-controlled phase lock and phase key) verifying mechanism provides a higher security strength. Acknowledgements This work is supported by the National Natural Science Foundation of China (61171073 and 61307003), China Figure 5. The output images of the authentication for various situations (the iteration times is fixed as 500, independence). Table 1. The CCs of the output images (as Figure 5) with the standard certification images. Phase key 1 Phase key 2 Phase key 3 Phase key 4 Phase key 5 Phase key 6 Phase lock 1 0.9721 0.2735 0.1211 0.2185 0.2125 0.3510 Phase lock 2 0.3211 0.9631 0.2260 0.3250 0.2411 0.2520 Phase lock 3 0.2255 0.3255 0.9711 0.2581 0.1854 0.2856 Phase lock 4 0.2865 0.3150 0.1865 0.9665 0.2652 0.3965 Phase lock 5 0.1353 0.3225 0.2151 0.1855 0.9855 0.2365 Phase lock 6 0.3525 0.2562 0.3550 0.2895 0.2568 0.9785  W. Q. He, X. Peng Postdoctoral Science Foundation (2013M540662) and the Sino-German Center for Research Promotion (GZ 760). References [1] Refregier, P. and Javidi, B. (1995) Optical Image Encryption Based on Input Plane and Fourier Plane Random Encod- ing. Optics Letters, 20, 767-769. http://dx.doi.org/10.1364/OL.20.000767 [2] Liu, S. T., Mi, Q.L. and Zhu, B.H. (2001) Optical Image Encryption with Multistage and Multichannel Fractional Fourier-Domain Filtering. Optics Letters, 26, 1242-1244. http://dx.doi.org/10.1364/OL.26.001242 [3] Mogensen, P.C., Eriksen, R.L. and Gluckstad, J. (2001) High Capacity Optical Encryption System Using Ferro-Elec- tric Spatial Light Modulators. Journal of Optics A: Pure and Applied Optics, 3, 10-15. http://dx.doi.org/10.1088/1464-4258/3/1/302 [4] Peng, X., Cui, Z.Y. and Tan, T.N. (2002) Information Encryption with Virtual-Optics Imaging System. Optics Com- munications, 212, 235-245. http://dx.doi.org/10.1016/S0030-4018(02)02003-5 [5] Situ, G. H. and Zhang, J. (2004) Double Random-Phase Encoding in the Fresnel Domain. Optics Letters, 29, 1584- 1586. http://dx.doi.org/10.1364/OL.29.001584 [6] Barrera, J.F., Henao, R. , Tebaldi, M., Torroba, R. and Bolognini, N. (2006) Multiplexing Encrypted Data by Using Po- larized Light. Optics Communications, 260, 109-112. http://dx.doi.org/10.1016/j.optcom.2005.10.053 [7] Chen, L.F. and Zhao, D.M. (2006) Optical Image Encryption with Hartley Transforms. Optics Letters, 31, 3438-3440. http://dx.doi.org/10.1364/OL.31.003438 [8] Zhou, N., Wang, Y. and Gong, L. (2011) Novel Optical Image Encryption Scheme Based on Fractional Mellin Trans- form. Optics Communications, 284, 3234-3242. http://dx.doi.org/10.1016/j.optcom.2011.02.065 [9] He, W.Q., Peng, X. , Qi n, W. and Meng, X.F. (2010) The Keyed Optical Hash Function Based on Cascaded Phase- Truncated Fourier Transforms. Optics Communications, 283, 2328-2332. http://dx.doi.org/10.1016/j.optcom.2009.11.060 [10] Carnicer, A., Montes-Usategui, M., Arcos, S. and Juvells, I. (2005) Vulnerability to Chosen-Ciphertext Attacks of Optical Encryption Schemes Based on Double Random Phase Keys. Optics Letters, 30, 1644-1646. http://dx.doi.org/10.1364/OL.30.001644 [11] Peng, X., We i, H. Z. and Zhang, P. (2006) Known-Plaintext Attack on Optical Encryption Based on Double Random Phase Keys. Optics Letters, 31, 1044-1046. http://dx.doi.org/10.1364/OL.31.001044 [12] Frauel, Y., Castro, A., Naughton, T.J. and Javidi, B. (2007) Resistance of the Double Random Phase Encryption against Various Attacks. Optics Express, 15, 10253-10265. http://dx.doi.org/10.1364/OE.15.010253 [13] Situ, G., Gopinathan, U., Monaghan, D.S. and Sheridan, J.T. (2007) Cryptanalysis of Optical Security Systems with Significant Output Images. Applied Optics, 46, 5257-5262. http://dx.doi.org/10.1364/AO.46.005257 [14] Tashima, H., Takeda, M., Suzuki, H., Obi, T., Yamaguchi, M. and Ohyama, N. (2010) Known Plaintext Attack on Double Random Phase Encoding Using Fingerprint as Key and a Method for Avoiding the Attack. Optics Express, 18, 13772-13781. http://dx.doi.org/10.1364/OE.18.013772 [15] Meng, X.F. , Cai, L.Z. and Wang, Y.R. (2007) Hierarchical Image Encryption Based on Cascaded Iterative Phase Re- trieval Algorithm in the Fresnel Domain. Journal of Optics A: Pure and Applied Optics, 9, 1070-1075. http://dx.doi.org/10.1088/1464-4258/9/11/017 [16] Zhang, Y. and Wang, B. (2008) Optical Image Encryption Based on Interference. Optics Letters, 33, 2443-2445. http://dx.doi.org/10.1364/OL.33.002443 [17] Wang, B. and Zhang, Y. (2009) Double Images Hiding Based on Optical Interference. Optics Communications, 282, 3439-3443. http://dx.doi.org/10.1016/j.optcom.2009.05.050 [18] Zhu, N. , Wang, Y.T., Liu, J., Xie, J. H. and Zhang, H. (2009) Optical Image Encryption Based on Interference of Pola- rized Light. Optics Express, 17, 13418-13424. http://dx.doi.org/10.1364/OE.17.013418 [19] Han, Y.J. and Zhang, Y.H. (2010) Optical Image Encryption Based on Two Beams’ Interference. Optics Communica- tions, 283, 1690-1692. http://dx.doi.org/10.1016/j.optcom.2009.12.060 [20] Tay, C.J., Quan, C., Chen, W. and Fu, Y. (2010) Color Image Encryption Based on Interference and Virtual Optics. Optics & Laser Technology, 42, 409-415. http://dx.doi.org/10.1016/j.optlastec.2009.08.016 [21] Kumar, P., Joseph, J. and Singh, K. (2011) Optical Image Encryption Using a Jigsaw Transform for Silhouette Remov- al in Interference-Based Methods and Decryption with a Single Spatial Light Modulator. Applied Optics, 50, 1805- 1811. http://dx.doi.org/10.1364/AO.50.001805 [22] Weng, D.D. , Zhu, N., Wa ng, Y.T., Xie, J.H. and Liu, J.A. (2011) Experimental Verification of Optical Image Encryp-  W. Q. He, X. Peng tion Based on Interference. Optics Communications, 284, 2485-2487. http://dx.doi.org/10.1016/j.optcom.2011.01.039 [23] Yang, B. , Liu, Z., Wang, B., Zhang, Y. and Liu, S. (2011) Optical Stream-Cipher-Like System for Image Encryption Based on Michelson Interferometer. Optics Express, 19, 2634-2642. http://dx.doi.org/10.1364/OE.19.002634 [24] Yuan, S., Yao, S.X., Xin, Y.H. and Liu, M. T. (2011) Information Hiding Based on the Optical Interference Principle. Optics Communications, 284, 5078-5083. http://dx.doi.org/10.1016/j.optcom.2011.07.015 [25] He, W.Q., Pen g, X. and Meng, X.F. (2012) Optical Multiple-Image Hiding Based on Interference and Grating Modula- tion. Journal of Optics, 14, Article ID: 075401. http://dx.doi.org/10.1088/2040-8978/14/7/075401 [26] Schneier, B. (1996) Applied Cryptography: Protocols, Algorithms, and Source Code in C. 2nd Edition, John Wiley & Sons, Hoboken.
|