 Journal of Computer and Communications, 2014, 2, 10-17 Published Online March 2014 in SciRes. http://www.scirp.org/journal/jcc http://dx.doi.org/10.4236/jcc.2014.24002 How to cite this paper: Babenko, L. and Maro, E. (2014) Algebraic Cryptanalysis of GOST Encryption Algorithm. Journal of Computer and Communications, 2, 10-17. http://dx.doi.org/10.4236/jcc.2014.24002 Algebraic Cryptanalysis of GOST Encryption Algorithm Ludmila Babenko, Ekaterina Maro Department of Information Security, Southern Federal University, Taganrog, Russia Email: marokat@gmail.com Received October 2013 Abstract This paper observes approaches to algebraic analysis of GOST 28147-89 encryption algorithm (also known as simply GOST), which is the basis of most secure information systems in Russia. The general idea of algebraic analysis is based on the representation of initial encryption algorithm as a system of multivariate quadratic equations, which define relations between a secret key and a cipher text. Extended linearization method is evaluated as a method for solving the nonlinear sys- tem of equations. Keywords Encryption Algorithm GOST; GOST⊕; S-Box; Systems of Multivariate Quadratic Equations; Algebraic Cryptanalysis; Extended Linearization Method; Gaussian Elimination 1. Introduction The general idea of algebraic cryptanalysis is finding equations that describe nonlinear transformations of S- boxes followed by finding solution of these equations and obtaining the secret key. This method of cryptanalysis belongs to the class of attacks with known plaintext. It is enough to have a single plaintext/ciphertext pair for the success. Algebraic methods of cryptanalysis contain the following stages: • Creation of the system of equations that describe transformations in non-linear cryptographic primitives of the analyzed cipher (i.e., S-boxes for most symmetric ciphers); • Finding solution of this system. The idea to describe an encryption algorithm as system of linear equations originated quite long time ago. However, until recent years it was a purely theoretical idea because it demanded huge memory capacities for storing variables and supplementary data. Nowadays, just a few research results are available that demonstrated the possibility to attack a full-round encryption algorithm. Analysis of full-round GOST is declared in paper [1]. However this paper does not contain any detailed description of the approach, only a brief outline. We will dis- cuss in detail the basic mechanisms of algebraic analysis with regard to GOST. 2. GOST Encryption Algorithm GOST encryption algorithm has four operation modes: simple substitution mode, stream mode, stream mode  L. Babenko, E. Maro with feedback and authentication mode. Simple substitution mode is the basic one and all other modes contain it in their structure. We will consider only this mode in the chapter. GOST algorithm is a symmetric block cipher, which conforms to Feistel scheme. 64-bit blocks of data are submitted to the input and converted into 64-bit blocks of encrypted data by 256-bit key. In each round the right side of plain text messages is processed by function F, which converts data with three cryptographic operations: adding data and subkey modulo 232, substitution of data using S-boxes, and left cyclic shift by 11 positions. Output of F-function is added modulo 2 to the left part of the plaintext, then right and left sides are swapped for next round. The algorithm has 32 rounds. In the last round of encryption right and left parts are not swapped. The overall dataflow diagram of GOST is shown in Figure 1. GOST uses 8 S-boxes, which convert 4-bit input to 4-bit output. Unlike most encryption algorithms, GOST has no predefined S-boxes and any values can be used for them. Secret key contains 256 bits and is represented as a sequence of eight 32-bit words: K1, K2, K3, K4, K5, K6, K7 and K8. In each round of encryption one of these 32-bit words is used as a round subkey. When round subkey is calculated, the following principle is used: from round 1 to round 24 the order is straight, (K1, K2, K3, K4, K5, K6, K7, K8, K1, K2, etc.); from round 25 to round 32 reversed order is used (K8, K7, K6, K5, K4, K3, K2, K1). 3. Algebraic Cryptanalysis Claude Shannon [2] assumed that cracking strong encryption algorithm requires “as much work as for solving simultaneous equations with a large number of the unknown variables”. While analyzing encryption algorithms much attention used to be directed to statistical analysis methods and algebraic attacks describing holistic ap- proaches to the problem of cipher strength analysis. The use of cipher internal structure is a characteristic property of algebraic analysis unlike statistical methods. Cryptanalyst reports enciphering transformation in terms of simultaneous equations and tries to solve the present simultaneous equation to obtain the encryption key. Algebraic attacks can be set as two stages. The first stage is to present an encryption algorithm and some extra algorithm data in a form of polynomial equation set over GF(2) field or other finite field. The second stage is to solve the simultaneous equations and obtain the encryp- tion key. Cryptanalyst should generally know μ pair, (P1,···, Pμ) plain text and (C1,···, Cμ) cipher text, when E(Pi) = Ci condition holds for any i {1, μ}. One or several solutions can be obtained in the course of algebraic analy- sis. In the simultaneous equation, set for the analyzed encryption algorithm, single unknown value corresponds to Figure 1. GOST encryption algorithm.  L. Babenko, E. Maro every key bit. Furthermore, there could be other unknown values connecting input and output encryption round values in the simultaneous equations. Cryptanalyst’s task is to construct a sufficient number of equations from algebraic analysis in order to reduce the number of solutions of simultaneous equations to only one correct solu- tion, but yet simultaneous equations should be solved within acceptable period of time. Fulfillment of the above conditions means that algebraic analysis attack will be performed faster than brute force attack. Different cryp- tanalysis approaches were developed to solve nonlinear systems of Boolean equations. Practical aspects of cryp- tanalysis state that methods based on linear approximations of initial system are the most efficient. One of the first algebraic methods used in cryptography is based on determining Grӧbner basis. One can take a close look at Buchberger algorithm for determining Grӧbner basis in [3-5]. Later Jean-Charles Faugère [6] rec- ommended using more efficient F4 and F5 algorithms for determining Gröbner basis. In cryptography the solution of system of nonlinear equations is NP complex task and requires exponential time. At the same time efficient solution algorithms of simultaneous linear equations can be used within polynomial time. Thus, if the number of unique monomials in the system is more or equal to the number of linearly inde- pendent equations, initial nonlinear system can be put in linear form with linearization method [7]. The lineari- zation method is based upon the substitution of all nonlinear elements for new variables. The linearization method can be represented in the following form. Suppose simultaneous linear equations are over GF(2) field with the equations are given by ,, , , 0 ijkijiki k ij i axxb xc⊕ ⊕= ∑∑ where xi, xj—variables; ai,j,k, bi,k, сk GF(2)—cons tants; k—equation number. Solution of the present simultaneous linear equations involves substitution of each nonlinear monominal term (xixj) for new unknown ug and solution of the resulting simultaneous linear equations with respect to new varia- bles, with further determination of the solutions for the initial simultaneous linear equations by solving xixj = ug, special systems for each solution of simultaneous linear equations. If nonlinearity degree for each equation is not more than d value, the number of variables in the resulting si- multaneous linear equations is not more than . Complexity of determining solutions for si- multaneous linear equations when using Gaussian algorithm and neglecting the complexity of special systems, is evaluated at O(t)3. Cryptanalyst should generate additional equations using mathematics, i.e. when variable products are substituted, the list of the system unknown increases (all the products are taken as self-unknowns). In [8] devised an advanced relinearization method. Aware that there are efficient solution algorithms of linear systems, Kipnis and Adi Shamir suggested reducing MQ-task to linear form by relinearization, and then obtaining additional system equations with the help of connection between new variables. Authors illustrated that for overdefined system of equations relinearization algorithm will be executed within polynomial time. In relineari- zation method all nonlinear elements are substituted for new variables as is in the case of linearization, and then the relations between the unknowns produce additional equations. For example, one can use the commutative law of multiplication. Let initial nonlinear system possesses {x1, x2, x3, x4} variables, then their products can be substituted in the following way: x1·x2 = y12, x1·x3 = y13, x1·x4 = y14, x2·x3 = y23, x2·x4 = y24, x3·x4 = y34, then the additional equations come out right: (x1·x2)·(x3·x4) = (x1·x3)·(x2·x4) y12·y34 = y13·y24, (x1·x3)·(x2·x4) = (x1·x4)·(x2·x3) y13·y24 = y14 ·y23, (x1·x2)·(x3·x4) = (x1·x4)·(x2·x3) y12·y34 = y14·y23. New yiyj monomials will appear in the system, they can be substituted for new variables and linear system can be solved. The present method made possible to solve many systems which were not solvable by linearization method. The weak point of relinearization method is its complexity. The complexity is difficult to estimate cor-  L. Babenko, E. Maro rectly and depends on the properties of the initial system. Extended Linearization method (XL) [9] can be evolution of relinearization method. The basis of XL method is to solve system of equations by linearization with linearly independent equations produced preliminarily. Addi- tional equations are formed with multiplication system initial equations by monomials of the specified degree. Let us assume that initial system results from m equations with n unknowns connecting encryption key and known data. Then eXtended Linearization algorithm is given by the following: • Evaluating of D parameter of eXtended Linearization method by: , if2 , 3, if2 nn Dmm n Dm = > = ≤ • Multiplication of all initial m system equations for every monomials to ≤D-2 degree. • Including additional equations, obtained on stage 2, into the initial system. • Substitution of all unknown products for new variables (system is reduced to a linear form) by linearization. • Solution of the obtained linear system by Gaussian elimination method. The attack complexity by eXtended Linearization corresponds to the complexity of finding the solution of li- near system. When using Gaussian elimination method for solution of linear system, XL complexity is calcu- lated by , / n n TDnm ω ω ω ≈≈ where 3—exponent of Gauss transformation. Extended Sparse Linearization algorithm (XSL) was developed in [10]. This method is used for the solution of sparse systems, i.e. systems of equations lacking many possible unknown products. XSL method includes 5 steps: • Analysis of initial system of equations and selection of a fixed list of monomials and equations for further usage. • Selection of Р parameter value and multiplication of the equations selected on the previous step and (Р-1) product results of the selected monomials. It is the principle step of XSL method where it necessary to obtain sufficient number of linearly independent equations. • Т’ method is additionally executed, where some selected equations multiplied by single variables. • The use of linearization method by representing each monomial in the form of a new variable. • Execution of Gaussian elimination method to find one or several solutions of the equation system. The vital difference between XL and XSL methods lies in that in XL method initial system equations are mul- tiplied by all possible monomials to the degree not more than D-2 (where D—attack property depending on the number of equations and the unknowns of the initial system). In XSL method several equations should be mul- tiplied by the monomials selected earlier. The research of applying algebraic attacks to block ciphers can be found in the following papers. In [11] pro- posed to represent the block cipher algorithm, Advanced Encryption Standard (AES), in the form of one equa- tion with a great number of unknown values over GF(2) field. For 128-bit AES cipher this equation included 250 unknowns and didn’t practically bring the threat to cipher strength. The obtain results showed that representing the block cipher algorithm in the form of polynomial equation doesn’t mean its algebraic attack vulnerabilities. In [12,13] there are further investigations of AES standard analysis. Thus in [14] authors described the attacks on simplified Serpent, Present and AES cipher algorithms, and illustrated potential vulnerability to algebraic at- tacks. Thesis work [13] described the analysis results of full version of AES-128 and Cryptomeria algorithms by finding Grӧbner basis. Article [15] describes attack on Data Encryption Standard (DES) cipher algorithm. In the present research the authors executed the attack on 6 full rounds of DES encryption with the only known open text/ciphertext pair. Book [16] allows taking a close look at algebraic attack on Keeloq block cipher. Article [17] describes the analysis results by SAT-solving method, 8 rounds of PRINTCipher-48 block cipher algorithm with two texts known and analysis of 9 rounds with processing some assumptions. Today, despite the growing interest to the algebraic attacks, the use of such attacks in Russian symmetric en-  L. Babenko, E. Maro cryption standard GOST is poorly reviewed. When reviewing GOST analysis, we should mark the work [1] it executed the attack 239 times as fast than brute force attack with known 264 texts. However, in this work the au- thor doesn’t reveal GOST attack algorithm, wh ich is why further research of GOST attack will be relevant. 4. GOST Algebraic Cryptanalysis Let’s review the use of algebraic attack on GOST with eXtended Linearization method. From the beginning the authors considered the attack on the light version of GOST. The present algorithm was chosen in view of sim- plifying of addition modulo 232 with round key in the system of equations. Thereafter when passing to GOST analysis addition modulo 232 with round key should be presented as additional equations as described in [14]. Basing on previous research of attack applicability to block ciphers, generation of equation system connecting cipher key and the known data is executed for nonlinear substitution transformation in GOST, presented by S-boxes. GOST substitution boxes are known to be additional secret encryption element, and accordingly the authors considered the implementation of attack preparatory stage directed to calculation of secret substitution tables [18]. The complexity of preparatory stage is not more than 232 encryption operations for unequivocal finding of substitution table. For recovery of substitution tables, as a part of study, required 230 encryptions and 26 minutes to calculate with IntelCore 2 Duo T8100 and memory capacity 2 GB. Algorithm of equation system generation for a fixed substitution table was illustrated in [19]. For the substitution boxes of 4 × 4 bit, described in [20], 237 possible equations were tested, and 221 equations appeared to be correct transformation of substitution block. 21 linearly independent equations were found for every block. Transformations in one encryption round were produced by the system which included 168 linearly independent equations with 64 unknowns and 288 various monomials. Linearly independent equations for the first substitution box under research are given by: x4 x4y2 x3y3 x3y1 x2y4 x2y1=0 x3 x3x2 x4y1 x3y3 x3y2 x2y4 x2y3 x2y2 x2y1 x1 x1y3 x1y2 x1y1=0 x2 x3x2 x2y3 x2y2 x2y1=0 x1 x4y1 x3y2 x2y4 x2y2 x2y1 x1y4 x1y3 x1y1=0 y4 x4y1 x3y1 x2y3 x2y1 x1y4 x1y3 x1y1=0 y3 x3x2 x2y2 x2y1 x1y4 x1y3 1=0 y2 x4y2 x1y2 x1y1=0 y1 x3y1 x2y3 x2y1 x1y3 x1y1=0 x4x3 x4y1 x3y4 x3y2 x3y1 x2y4 x2y2 x2y1 x1y4 x1y2 x1y1=0 x4x2 x4y1 x3y2 x1y3 x1y1=0 x4x1 x4y1 x3y4 x3y1 x2y4 x2y3 x2y2 x2y1 x1y4 x1y2=0 x3x1 x3y3 x3y1 x2y2 x1y4 x1y3 x1y2=0 x2x1 x4y1 x3y4 x3y1 x2y4 x2y3 x2y1 x1y4 x1y2 x1y1=0 y4y3 x4y1 x3y4 x3y2 x2y4 x2y2 x2y1 x1y4 x1y3 x1y2 x1y1=0 y4y2 x4y1 x3y2 x2y4 x2y2 x2y1 x1y3 x1y2 x1y1=0 y4y1 x3y3 x3y2 x2y4 x2y3 x1y1=0 y3y2 x4y4 x4y2 x4y1 x3y3 x3y2 x3y1 x2y4 x2y1 x1y1=0 y3y1 x4y4 x4y1 x3y4 x2y4 x2y3 x2y2 x2y1 x1y4 x1y2=0 y2y1 x4y4 x3y2 x1y3=0 x4y4 x3y4 x3y3 x3y2 x2y3 x2y2 x1y4 x1y3 x1y2 x1y1=0 x4y3 x4y2 x4y1 x3y4 x3y1 x2y4 x2y2 x2y1 x1y4 x1y3 x1y2=0 For two GOST rounds showed in Figure 2, the initial system depicting encryption transformation includes 336 equations, 128 unknowns and 576 various monomials. Using linearization method without additional re- ducing will not allow finding the solution as the number of equations is less than the number of monomials. Us- ing GOST structure one can substitute output bits of substitution boxes for evaluated values by formulas: Y1 = (PL CR)>>>11, for the first round, Y2 = (PR CL)>>>11, for the second round. After substitution the system will obtain 64 unknowns instead of 128 and the number of monomials in the equations will be reduced to 160. The requirement of linearization applicability will be fulfilled, thus, we will apply linearization method to find encryption key for two GOST rounds in the second attack stage. As it was mentioned above, the attack complexity defines the complexity of linear system solution, so the cryptanalysis  L. Babenko, E. Maro Figure 2. Two GOST rounds in ordinary substitution mode. complexity of two GOST rounds is 1603 ≈ 222, which is in 242 times less than the complexity of brute force at- tack (264). The attack on two rounds of GOST algorithm was similar to the attack on two rounds of GOST encryption algorithm. The system of equations remains the same for GOST algorithm but round key calculation with the obtained input values of substitution boxes was affected. Being aware that addition is performed according to modulo 232, translation between digits was verified when sum calculation. For example, let us take original at- tack data as following: Plain text 58b7e5e8a13a Cipher text c3a09d847e1aa55e The input value of substitution boxes was calculated: X1 = 95771861 X2 = 2DA91C85 If we know substitution box inputs, we can calculate round encryption keys by formulas: K = PR + X, if X > PR K = 232 − PR + X, if X ≤ PR We have found the following keys for two rounds: K1 = AF8E7727 K2 = AF8E7727 When passing to the analysis of three GOST encryption rounds illustrated in Figure 3, the system with 504 equations, 192 unknowns and 864 various monomials. Reduction of the number of the system unknowns for three rounds was not successful and searching of the solution was executed with XL method. When applying eXtended Linearization method the authors consider every substitution box individually. In this case D parameter of XL method is equal to 3, i.e. each of 21 equa- tions for substitution box is multiplied by the unknown to 1 extent. Then we obtain 189 equations for one subs- titution box, the majority of these equations are linearly independent. For three encryption rounds after resulting in additional equations, the system includes 4536 equations with 192 unknowns and 2208 various monomials. The system can be solved by linearization. Attack complexity for GOST encryption rounds will be 22083 ≈ 234 that is in 262 times less than complexity of finding round keys with brute force method. For 32-round GOST encryption algorithm the system will contain 48,384 equations with 2048 unknowns and 23,552 various monomials. Attack complexity will be 23,5523 ≈ 244. Note that implementation of GOST attack algorithms mentioned above with GOST cipher attack is com- plicated by translation between digits when addition modulo 232 with round key. Implementation of unfixed 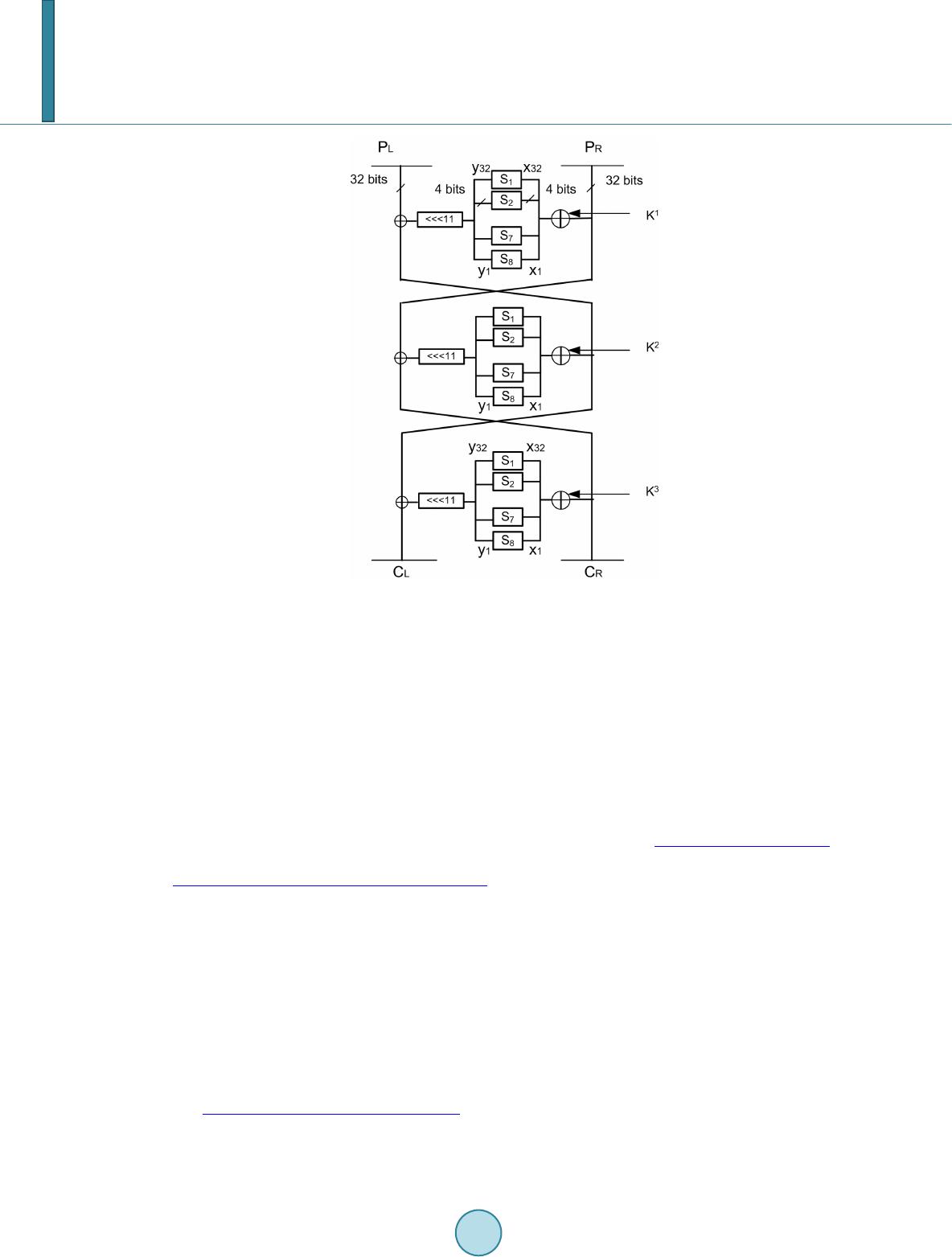 L. Babenko, E. Maro Figure 3. Three rounds of GOST encryption algorithm. substitution tables is the difference between attack on GOST algorithms and GOST in comparison with other box ciphers, that every time provokes the necessity to restore substitution tables and generate system of equa- tions. It is noteworthy that there is a possibility of efficient parallelization of equation system generation for substitution boxes and solution of simultaneous linear equations. Nowadays the implementation of eXtended Linearization algorithms for GOST full-function 32-round algo- rithm is still under investigation. This research was supported by Russian Foundation for Basic Research (RFBR), projects No. 12-07-31032 and 12-07-33007. References [1] Courtois, N. (2011) Algebraic Complexity Reduction and Cryptanalysis of GOST. http://eprint.iacr.org/2011/626 [2] Shannon, C.E. (1949) Communication Theory of Secrecy Systems. Bell Systems Technical Journal, 28, 656-715. http://dx.doi.org/10.1002/j.1538-7305.1949.tb00928.x [3] Becker, T. and Weispfenning, V. (1993) Grӧbner Bases: A Computational Approach to Commutative Algebra (Cor- rected Edition). Springer-Verlag, New York. [4] Cox, D. A., Little, J.B. and O’Shea, D. (1996) Ideals, Varieties, and Algorithms. 2nd Edition, Springer-Verlag, New York. [5] Kalkbrener, M. (1999) On the Complexity of Gröbner Bases Conversion. Journal of Symbolic Computation, 28, 265- 273. [6] Faugère, J.-C. (2002) A New Efficient Algorithm for Computing Grӧbner Bases without Reduction to Zero (F5). Pro- ceedings of the 2002 International Symposium on Symbolic and Algebraic Computation (ISSAC’02), Association for Computing Machinery, Inc., New York, 75-83. [7] Courtois, N., Goubin, L., Mei er, W. and Tacier, J.-D. (2002) Solving Underdefined Systems of Multivariate Quadratic Equations. In: Public Key Cryptography, Lecture Notes in Computer Science, Vol. 2274, Springer, New York, 211- 227. http://dx.doi.org/10.1007/3-540-45664-3_15 [8] Kipnis, A. and Shamir, A. (1999) Cryptanalysis of the HFE Public Key Cryptosystem by Relinearization. Advances in Cryptology-Crypto’99, Lecture Notes in Computer Science, Vol. 1666, Springer, New York, 19-30.  L. Babenko, E. Maro http://dx.doi.org/10.1007/3-540-48405-1_2 [9] Courtois, N., Klimov, A., Patarin, J. and Sha mir, A. (2000) Efficient Algorithms for Solving Overdefined Systems of Multivariate Polynomial Equations. Advances in Cryptology—EUROCRYPT, Lecture Notes in Computer Science, Vol. 1807, New York, Springer, 392-407. [10] Courtois, N. and Piep rzy k, J. (2002) Cryptanalysis of block ciphers with overdefined systems of equations. Asiacrypt, Lecture Notes in Computer Science, Vol. 2501, Springer, New York, 267-287. [11] Ferguson, N. , Schroeppel, R. and Whiting, D. (2001) A Simple Algebraic Representation of Rijndael. Proceedings of Se- lected Areas in Cryptography, Springer-Verlag, New York, 103-111. http://dx.doi.org/10.1007/3-540-45537-X_8 [12] Courtois, N. a nd Debraize, B. (2008) Specific S-Box Criteria in Algebraic Attacks on Block Ciphers with Several Known Plaintexts. Research in Cryptology, Lecture Notes in Computer Science, Vol. 4945, Springer, New York, 100- 113. http://dx.doi.org/10.1007/978-3-540-88353-1_9 [13] Weinmann, R.-P. (2009) Algebraic Methods in Block Cipher Cryptanalysis. Ph.D. Thesis, Technische Universität, Darmstadt. [14] Courtois, N. and Debraize, B. (2008) Algebraic Description and Simultaneous Linear Approximations of Addition in Snow 2.0. The 10 th International Conference on Information and Communications Security (ICICS), Lecture Notes in Computer Science, Vol. 5308, Springer, New York, 328-344. [15] Courtois, N. and Bard, G.V. (2007) Algebraic Cryptanalysis of the Data Encryption Standard. In Cryptography and Coding, 11th IMA Conference, Springer, New York, 152-169. [16] Bard, G.V. (2009) Algebraic Cryptanalysis. Springer, New York. http://dx.doi.org/10.1007/978-0-387 -88757-9 [17] Bulygin, S. (2011) Algebraic Cryptanalysis of the Round-Reduced and Side Channel Analysis of the Full PRINTCi- pher-48. http://eprint.iacr.org/2011/287.pdf [18] Saarinen, M.-J. (1998) A Chosen Key Attack against the Secret S-boxes of GOST. http://www.researchgate.net/publication/2598060_A_chosen_key_attack_against_the_secret_S-boxes_of_GOST [19] Babenko, L.K., Ishchukova, E.A. and Ma ro, E.A. (2011) Algebraic Analysis of GOST Encryption Algorithm. Pro- ceedings of the 4th International Conference of Security of Information and Networks, Association for Computing Machinery Inc., New York, 57-62. [20] Popov, V., Kurepkin, I. and Leontiev, S. (2006) Additional Cryptographic Algorithms for Use with GOST 28147-89, GOST R 34.10-94, GOST R 34.10-2001, and GOST R 34.11-94 Algorithms. http://www.ietf.org/rfc/rfc4357
|