Journal of Computer and Communications, 2014, 2, 1-9
Published Online March 2014 in SciRes. http://www.scirp.org/journal/jcc
http://dx.doi.org/10.4236/jcc.2014.24001
How to cite this paper: Ghafar, A.H.A. and Ariffin, M.R.K. (2014) Timing Attack Analysis on AAβ Cryptosystem. Journal of
Computer and Communications, 2, 1-9. http://dx.doi.org/10.4236/jcc.2014.24001
Timing Attack Analysis on AAβ Cryptosystem
A. H. A. Ghafar1, M. R. K. Ariffin2
1Al-Kindi Cryptography Research Laboratory, Institute for Mathematical Research, Universiti Putra Malaysia
(UPM), Serdang, Malaysia
2Mathematics Department, Faculty of Science, Universiti Putra Malaysia (UPM), Serdang, Malaysia
Received September 2013
Abstract
Timing attack is an attack on the implementation of a cryptographic primitive. The attack collects
leaked secret data via certain implementation techniques either on software or hardware. This
paper provides an analysis of a theoretical timing attack on the AAβ algorithm. The attack dis-
cussed in this paper gives avenues for secure implementation of AAβ against timing attacks. The
simulation of the attack is important to provide invulnerability features for the algorithm in order
to be implemented and embedded on applications. At the end of the attack, a method to overcome
it will be introduced and it is called AAβ blinding.
Keywords
Timing Attack; Side-Channel Attack; Public-Key Cryptosystem; AAβ Public Key Cryptosystem
1. Introduction
The
AA
β
cryptosystem utilizes the integer factorization problem (IFP) coupled with the square root problem as
its cryptographic primitive. The algorithm claims to have a complexity order of
2
()On
compared to renowned
RSA and ECC algorithms which both have
3
()On
in encryption and decryption process [1]. Although Rabin
cryptosystem also shares the same cryptographic primitive, but its decryption is 4-to-1 which makes the de-
crypted plaintext hard to distinguish. But
AA
β
overcomes this decryption failure without losing computational
power and speed.
Several cryptanalysis have been conducted on this cryptosystem and have pointed out that to find solution for
the cryptosystem is infeasible [1]. However, this cryptosystem has never been analyzed or attacked from imple-
mentation point of view. The reason for this is because
AA
β
has not yet been implemented in a real-world
application. Nevertheless, it is important to launch a theoretical attack on its implementation to provide future
guidance for future implementers. This paper intends to do that and we will use one common type of side chan-
nel attack which is timing attack.
Timing attack uses leaked information of a cryptographic implementation to derive the secret keys of crypto-
graphic primitives. The first timing attack was developed to recover secret key, d in RSA implementation of
smart card [2]. Consider we have decryption equation of RSA
(mod )
d
MC N≡
for
C
is n-bit number and
d
is
k
-bit number. By measuring the computational time of the RSA decryption, the attack is able to collect
the private key bit per bit. In many cases, the attacker has unlimited access to the decryption machine but does

A. H. A. Ghafar, M. R. K. Ariffin
2
not have any knowledge about the secret key.
In order to prevent this kind of attack on RSA, Rivest introduced a defense mechanism called RSA blinding
[3]. It works by generating a random number,
r
which will ’blind’ the product of
(mod )
d
CN
and essentially
makes it impossible for attacker to determine the computational time. We will make use of this blinding concept
to come out with our own strategy for the
AA
β
algorithm. Like the RSA, random numbers also play a role in
our blinding mechanism to make sure that the decryption process time will be obscured.
This paper is structured as follows. Section 2 will dive into some algorithms that are commonly used to op-
timize both modular multiplication and exponentiation. Section 3 gives an overview of
AA
β
algorithm while
we will discuss on how timing attack is to be conducted on the algorithm in Section 4. We will also discuss the
AA
β
blinding in Section 5 to prevent any further timing attack on it in the future. Future works and conclusion
are in Section 6 and 7 respectively.
2. Design of Timing Attacks on Modular Exponentiation and Multiplication
The process of modular exponentiation and modular multiplication is essentially very time consuming process
especially when involves exponentiation of very large integers. They can slow down the whole process of de-
cryption and this is non-economical in commercial applications such as smart cards and real-time web commu-
nication which need fast response time. However, various methods have been introduced to speed up both oper-
ations.
First and the most basic method to increase the computational speed of this equation is repeated squaring al-
gorithm. This algorithm is mostly used in power constrained hardware such as smart card due to its low com-
plexity in calculation. However, it was exploited by Kotcher in the earliest timing attack on cryptosystem’s
hardware. Consider the decryption process of RSA.
(mod )
d
PC N≡
Kotcher cleverly observes this process as signal which has been corrupted by the ’noise’ of unknown bits of
d
. The attack emulates the decryption process and captures the calculated time of decryption using chosen pri-
vate keys until each bits of actual
d
is exposed.
Generally, for chosen private keys,
u
and
v
which have size of -bits
011 11
, ,,,0,,,
i inn
u uuuuuu
−+ −
=……
011 11
, ,,,0,,,
i inn
v vvvvvv
−+ −
=……
the only difference between both chosen private keys is bit at point
i
(Assume that both
u
and
v
already
have same arrangement of bits with actual private key,
d
up until position
? i1−
).
Let
j
C
be the calculation time to complete decryption using the actual private key,
d
. Also let
u
T
be the
calculation time from bit
0
u
to
i
u
using first emulated key,
u
and
v
T
be the calculation time from bit
0
v
to
i
v
using second emulated key,
v
. We assign
( )
,,uvj uv
T CT
′= −
Hence, variance of timing after point i for both
u
and
v
are regarded as
( )
( )
varvarvar( )
juu e
CTT T
′
−= +
and
( )
( )( )
varvar var
jvve
CTTT
′
−= +
where
e
T
is the measurement error. If we assume
u
has the correct bit (i.e.
d
has bit 0 at point
i
), then
()( )
var var
uv
TT
′′
<
due to increased similarities in
u
in terms of bits compared to
v
.
However, this kind of attack is only successful if the implementation uses repeated squaring algorithm. In
more advanced RSA implementations, repeated squaring algorithm is complemented with Montgomery reduc-
tion algorithm for every multiplication operation. Montgomery reduction algorithm, skips modular reduction

A. H. A. Ghafar, M. R. K. Ariffin
3
which uses the ‘expensive’ division operation. Montgomery reduction transforms the multiplication of
(mod )ab N⋅
to
(mod )and(mod )aaRN bbR N
′′
= =
for which we said
a′
and
b′
are in Montgomery form and
2
k
R=
for
k∈
[4]. The algorithm executes
multiplication in
R
reduction where a computer can easily and cheaply calculate because the division of
2
k
in binary is just a simple shift by
k
bits. One good explanation and example of Montgomery reduction can be
read here [5]. The pseudo codes of both algorithms and how they work together are explained in Algorithm 1.
To calculate modular exponentiation, most implementations use the Chinese Remainder Theorem (CRT) ap-
proach. This approach divides the modular exponentiation which is in the form of modular
N pq= ⋅
to the
form of modulo
p
and
q
. Values of
p
and q are normally stored in decryption machine. The logic behind
this approach is because the value of
p
and
q
are smaller than
N
, hence the modular exponentiation will be
more computationally efficient due to their decreased size. To get the original result, the results in modulo
p
and modulo
q
are combined.
Later, Schindler produced a significant observation for RSA implementation that uses repeated squaring, CRT
and Montgomery reduction approach [6]. Schindler observes that the extra reduction in Montgomery algorithm
to ensure
sN ≤
(refer Algorithm 2) caused atiming difference for different
a
and
b
. From this observa-
tion, Schindler derived the probability of an extra reduction occurring for
(mod )
d
p
ap
which is
(mod )
(extra reduction)2
ap
PR =
(1)
Observation from (1) shows that there is discontinuity after certain number of extra reduction process which
happens to be a multiple of
p
.
When a is approached by values less than a multiple of
p
as shown in Figure 1, number of reduction
Algorithm 1. Repeated squaring algorithm.
Algorithm 2. Montgomery algorithm.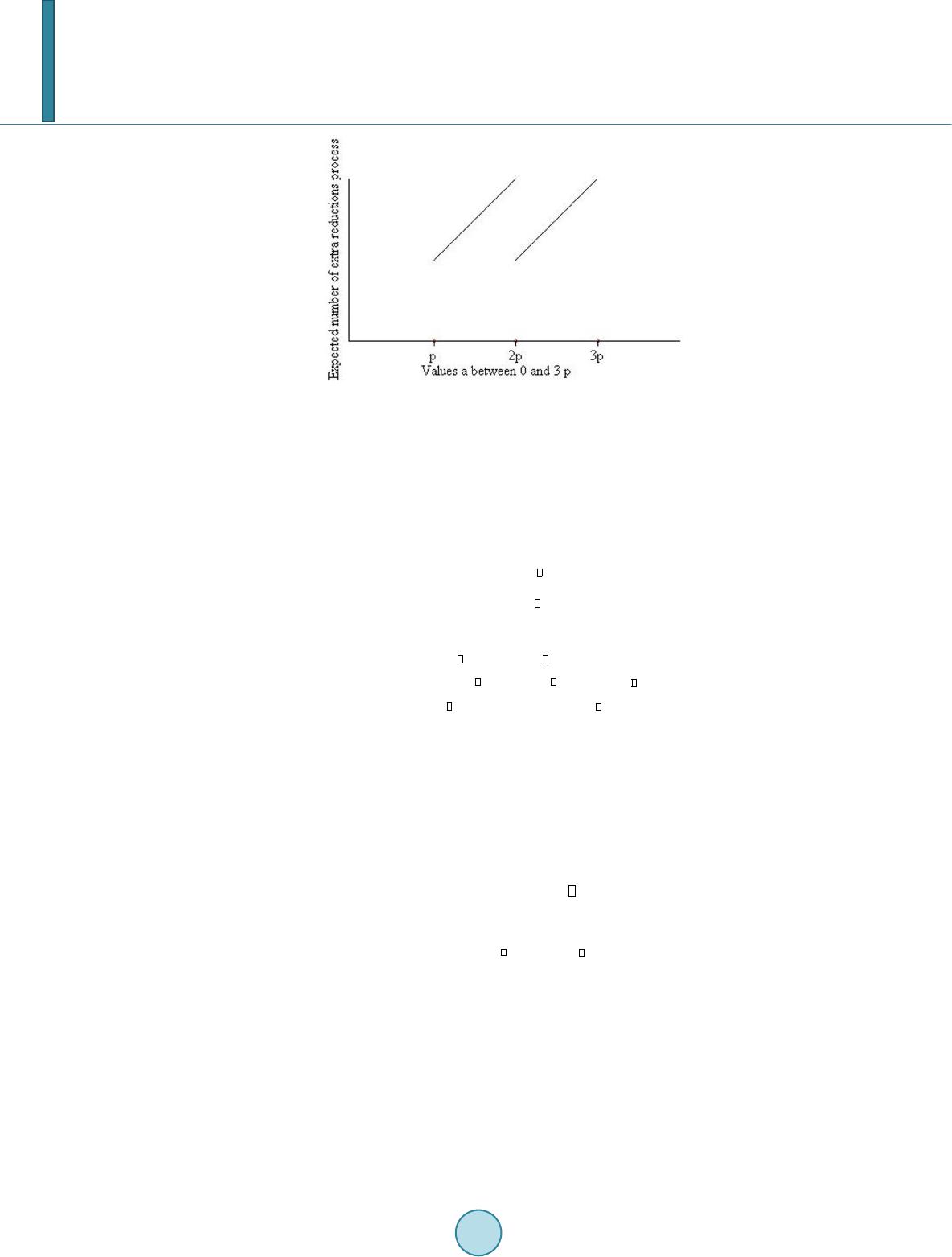

A. H. A. Ghafar, M. R. K. Ariffin
4
Figure 1. Number of extra reductions in a Montgomery re-
duction as function (1) of the input a.
increases. But, right after the multiple of
p
, the number of extra reduction drops significantly. This drop can
help us to derive the multiple of
p
hence factorize
N
.
Another algorithm known as the Karatsuba multiplication is regarded as the most efficient multiplication al-
gorithm of two numbers with the same numbers of digits [7]. This works by assuming that addition is much
cheaper than multiplication operation. The algorithm is explained as follows.
Given that we want to multiply
a
and
b
that have n numbers of digits. We can write
? 1
01
10
n
aa a
−
= +⋅
? 1
01
10
n
bb b
−
= +⋅
Basic arithmetic shows that
( )
()
??
?? ?
??
11
01 01
11
21
0 0011011
121
0 0011011
(10 )(10 )
1010 10
10 10
nn
nn n
nn
abaabb
ab ababab
abab abab
−−
−− −
−−



⋅=+⋅+ ⋅
=+⋅ +⋅ +⋅
= +++⋅
If we define
0 00
z ab=
10110
zab ab= +
2 11
z ab=
It is easy to see that
?210 1010 zaabbzz


 


=−− −−
And the product of
a
and
b
is
( )
?? 121
01 2
1010 .
nn
ab zzz
−−


+
 
 
⋅= +⋅⋅
Karatsuba algorithm cuts the work factor
2
()On
in long normal multiplication to only
1.585
()On
.
Both Montgomery multiplication and Karatsuba algorithm have been extensively used in real implementation
of RSA. RSA implementation in OpenSSL used repeated squaring, Montgomery multiplication and sliding
windows while utilized Karatsuba when multiplying a and b that have same size.
There are two vulnerabilities which have been exploited in this attack. First is the extra reduction happened in
Montgomery algorithm. This has been explained in Schindler’s attack while the other is the usage of long
multiplication and Karatsuba algorithm. Both multiplications show different time significantly [8]. Brumley and
Boneh showed how a timing attack launched on RSA implementation in OpenSSL [9]. The attack is so elegant,
it was done remotely between two servers in two different buildings. Every time the Mongomery form of C

A. H. A. Ghafar, M. R. K. Ariffin
5
slightly moves toward less than
p
, the number of extra reductions in the Montgomery reduction (Algorithm 2)
increases. It involves the multiplication of two numbers that are about the same size hence Karatsuba
multiplication is used. Meanwhile, whenever the value of
C
moves to be larger than
p
, the re- duction in
Algorithm 2 will decrease. Long multiplication is used here because the multiplication involves two numbers
that have significant different sizes.
The attack’s aim is to find the binary structure of
p
:
( )
0111 2
,,, ,,,,
ii nn
pbbb bbb
−−
=……
where
01b=
and has size of
n
-bits. This will solve the factorization of
N pq= ⋅
and lead to a total break of
RSA algorithm. The following method is used to recover the bit of
p
at point-
i
:
1) Suppose that bits of
p
have been determined from
0
b
to
1i
b
−
. Let
( )
0 011
, ,,,0,0,0
i
C bbb
−
=……
and
( )
1 011
,,,,1,0, 0
i
C bbb
−
= ……
That is, the only difference between the two chosen ciphertexts is the bit at point-
i
.
0
C
and
1
C
are the
candidates of prime
p
.
2) Assign
0
()TC
and
1
() TC
as the measured decryption times for
0
C
and
1
C
respectively.
3) Assign
( )
01
()TC TC∆= −
i.e the timing difference between
0
()TC
and
1
()
TC
.
4) If
01
C pC<<
, then
∆
is “large”. This indicates
0
i
b=
. If
01
CCp<<
, then
∆
is “small”. This
indicates
1
i
b=
. The thresholds of “large” and “small” are set by the previous values of
∆
.
5) The previous steps are repeated to obtain bits at points
123
,,,
ii i
bbb
++ +
…
until half of the bits
p
have been
recovered.
After obtaining half of bits of
p
, Coppersmith has extensive methods to recover the whole bits of
p
and
consequently factorizes
N
[10]. Value of

reveals whether extra reductions of Montgomery multiplication
or multiplication (normal versus Karatsuba) predominates during the decryption process at point
i
.
3. AAβ Algorithm
The Rabin cryptosystem utilized the square root modulo problem as its cryptographic primitive [11]. The
alluring factor in Rabin cryptosystem is it has a very small exponent key,
2e=
. But the cryptosystem has a
decryption failure which is caused by the 4-to-1 mapping during decryption. This trade-off deterred Rabin
cryptosystem to be widely used in modern application.
In 2013, Ariffin et al. proposed a new cryptosystem which also utilized the same problem but without any
decryption failure. The algorithm is workable with lower complexity order compared to DHKE, El-Gammal,
RSA and ECC [1]. Algorithms 3-5 show the whole cryptosystem.
The decryption algorithm uses multiplication together with a one time modular reduction. This lack of
expensive operation makes
AA
β
to be an ideal candidate for future public key cryptosystem.
We now analyze the operation given by
(mod )WC dpq≡⋅
Algorithm 3. AAβ key generation.

A. H. A. Ghafar, M. R. K. Ariffin
6
Algorithm 4. AAβ encryption.
Algorithm 5. AAβ dec ryption.
and discuss whether the time calculation of this operation can be exploited. Later, we will enhance the capability
of an attacker to obtain
W
which consequently will continue onto the calculation of
1
4(mod )
p
p
xW p
+
≡
and
1
4
(mod )
q
q
xW q
+
≡
assuming that we can distinguish the operational time for all multiplications that occurs within the decryption
machine. In the next section, we will show how the attack is launched on the
AA
β
decryption algorithm.
4. Timing Attack on AAβ Algorithm
From Section 2, it is obvious that timing attack manipulates the timing difference in exponentiation multiplica-
tion with the aim to find first, the bits of private key bit per bit and second, factor
N pq= ⋅
(i.e. for a public
key cryptosystem which accommodates hard factorization problem as its underlying strength). We have also
observed the multiple stages of the decryption algorithm of
AA
β
(Algorithm 5) in Section 3. Despite its
intricacy, the algorithm is still faster than RSA. Since this paper only discusses the theoretical analysis of timing
attack due to lack of real-world implementation of
AA
β
algorithm, it is reasonable to assume that future
implementation of this algorithm will adhere to the vastly used implementation in terms of multiplication and

A. H. A. Ghafar, M. R. K. Ariffin
7
modular exponentiation. Based on this assumption, we now observe the first multiplication in the
AA
β
decryption algorithm which is
(mod ) WC dpq≡⋅
(2)
Since
7
~2n C
and
2
~2
n
d
, the inequality in the size of
C
and
d
will not give us a choice to use
Karatsuba reduction in the implementations of
AA
β
. This is because Karatsuba algorithm requires both
multiplication elements to be in the same size to make it efficient as stated in Section 2.
As for other method, Montgomery multiplication, it is also not practical in this multiplication process because
the reduction only works better than long multiplication if there is an exponentiation operation involved.
However Equation (2) does not involve exponentiation.
In short, to compute
Cd⋅
efficiently, one only use long multiplication. Next, we increase the advantage for
the attacker by assuming that value
W
can be manipulated or collected. This loose assumption is realistic due
to misuse implementation or hardware faulty. We also assume that equation
( )
p1
4
p
xmod pW
+
≡
(3)
is implemented using the same method of RSA SSL implementation. Implementors are lured to the same
method because the method can use dynamically Montgomery and Karatsuba multiplication for fast modular
exponentiation—depends on the exponents given.
If that is the case, we will show that
p
can be obtained by measuring computational time of (3), using the
same method by Brumley and Boneh which eventually gives out
p
. The method is as follows:
1) Suppose that bits of p have been determined from
0
b
to
1i
b
−
. Let
( )
0 011
, ,,,0,0,0
i
W bbb
−
=……
and
( )
1 011
,,,,1,0, 0
i
W bbb
−
= ……
that is, the only difference between the two chosen ciphertexts is the bit at point-
i
.
0
W
and
1
W
are the
candidates of prime
p
.
2) Assign
0
()TW
and
1
()TW
as the measured decryption times for
0
W
and
1
W
respectively.
3) Assign
( )
01
()TW TW∆= −
i.e. the timing difference between
0
()TW
and
1
()
TW
.
4) If
01
W pW<<
, then
∆
is “large”. This indicates
0
i
b=
. If
01
WWp
<<
, then
∆
is “small”. This
indicates
1
i
b=
. The thresholds of “large” and “small” are set by the previous values of
∆
.
5) The previous steps are repeated to obtain bits at points
123
,,,
ii i
bbb
++ +
…
until half of the bits
p
have been
recovered.
It is clear that
AA
β
is susceptible to timing attack if value of
W
is leaked. Hence further improvement is
needed to overcome the attack. Section 5 will show how this kind of attack can be addressed by a method called
AA
β
blinding.
5. AAβ Blinding
We begin this section under strong assumption that a timing analysis can be conducted upon
Cd⋅
prior to
compute
W(mod )C dpq≡⋅
and an attacker would be able to derive the private key d bit per bit. Hence there
is a need to blind the multiplication process of
Cd⋅
before the modulo reduction of
pq
. We called this
process as
AA
β
blinding.
Based on its name, it is clear that the method uses the same principle with RSA blinding.We will introduce a
random number,
r
into
AA
β
decryption algorithm. Instead of deterministic decryption of time, the algorithm
will have randomized timing decryption. The randomization will increase the difficulty for the adversary to find
out the exact value of the private key,
d
. The alteration occurs within the
AA
β
decryption algorithm
(Algorithm 5); starting from Step 1. The procedure is detailed in Algorithm 6.
Observe
1()(mod )WCrQpq≡⋅⋅
and

A. H. A. Ghafar, M. R. K. Ariffin
8
Algorithm 6. AAβ blinding.
( )
2
mod .WC Rpq≡⋅
This value will be computed in
p1
4
12
()(mod )
p
x WWp
+
≡+
and
( )
1
4
12
()mod .
q
q
x WWq
+
≡+
It is easy to see that
( )
11
44
12
11
44
()()(mod )
( ())(mod)()mod.
pp
pp
WWCrQ CRp
CrQ RpCdp
++
++
+≡⋅⋅ + ⋅
≡⋅+≡ ⋅
and
( )
11
44
12
11
44
()()(mod )
(())(mod )()mod.
qq
qq
WWCrQ CRq
CrQ RqCdq
++
++
+≡⋅⋅ + ⋅
≡⋅+≡ ⋅
which are exactly following the original steps 5 and 6 in Algorithm 5.
By using this blinding method, we change the deterministic characteristic in the decryption algorithm to a
probabilistic one. The size of randomized element, r is
n
-bit which makes it infeasible to be determined. We
will now simulate an example.
Example Let
16n=
. Along will choose primes,
53887p=
,
53891q=
and
4070567597N=
. We
choose
6381159375677d=
and
544373306496r=
randomly.
We obtain
1004100545Q=
dna
21477. R=
The public keys are
1)
1
156489158370179
A
e=
2)
2
12180361837718376
A
e=
Let the derivatives of the messages that Busu want to send are
1)
9414048941460394886U=
2)
1281821555V=
Thus,
21486341075284587745963757517831994C=
. The blinding starts when
1
2
mod4070567597 1344015274mod4070567597
mod 2175088081mod4070567597
W CrQ
WC Rpq
≡ ⋅⋅≡
≡⋅ ≡
and Along obtains
53888
4
53892
4
(134401527 2175088081)mod5388711486mod53887
(1344015274 2175088081)mod5389124120mod53891
p
q
x
x
≡+ ≡
≡+ ≡
Further calculation based on Algorithm 5 successfully get back
1
V 1281821555=
and consequently
1
U 9414048941460394886=
.
6. Future Works
Many aspects of side-channel attacks have not been tested yet on the
AA
β
cryptosystems. Other types of
attacks are the differential power analysis attack and the glitching attack because it follows the same methodolgy

A. H. A. Ghafar, M. R. K. Ariffin
9
with the timing attack that has been discussed in this paper.
Furthermore, a deeper analysis is required to test the randomness generated in
AA
β
blinding to make sure
that the decyrption algorithm will always be a probabilistic process.
7. Conclusion
AA
β
decryption algorithm is susceptible to timing attacks that simulates the Brumley and Boneh attack on SSL.
However, a method to randomize the output on
AA
β
can overcome this problem. The blinding process changes
the deterministic characteristic in the decryption algorithm to become probabilistic and this makes the data
sampling procedure for the attack infeasible.
References
[1] Ariffin, M.R.K., et al. (2013) A New Efficient Asymmetric Cryptosystem Based on the Square Root Problem. Malay-
sian Journal of Mathematical Sciences, 7, 19-37.
[2] Kocher, P. (1996) Timing Attacks on Implementations of Difie-Hellman, RSA, DSS, and Other Systems. CRYPTO’96,
Santa Barbara, 18-22 August 1996, 104-113.
[3] Kaliski, B. (1996) Timing Attacks on Cryptosystems. RSA Laboratories Bulletin, 2.
[4] Montgomery, P. (1985) Modular Multiplication with Trial Division. Mathematics of Computation, Mathematics of
Computation, 44, 519-521. http://dx.doi.org/10.1090/S0025-5718-1985-0777282-X
[5] Buell, D.A. (2005) Montgomery Multiplication. http://cse.sc.edu/buell/csce557/Dlecturenotes/
[6] Schindler, W. (2000) A Timing Attack against RSA with the Chinese Remainder Theorem. Workshop on Cryptogra-
phic Hardware and Embedded Systems 2000 (CHES 2000), Worcester, 17-18 August 2000, 109-124.
[7] Karatsuba, A. and Ofman, Y. (1963) Multiplication of Many-Digital Numbers by Automatic Computers. Physics-Dok-
lady, 7, 595-596.
[8] Stamp, M. and Low, R.M. (2004) Applied Cryptanalysis. John Wiley & Sons Inc., Hoboken.
[9] Brumley, D. and Boneh, D. (2003) Remote Timing Attacks Are Practical. Proceedings of 12th Conference on USENIX
Security Symposium, 4-8 August 2003, Washington DC.
[10] Coppersmith, D. (1997) Small Solutions to Polynomial Equations, and Low Exponent RSA Vulnerabilities. Journal of
Cryptology, 10, 233-260. http://dx.doi.org/10.1007/s001459900030
[11] Rabin, M.O. (1979) Digitalized Signatures and Public Key Functions as Intractable as Factorization. MIT Laboratory
for Computer Science, MIT/LCS/TR-212.