J. Biomedical Science and Engineering, 2009, 2, 158-165
Published Online June 2009 in SciRes. http://www.scirp.org/journal/jbise
JBiSE
A muscle spindle model and study the effects of static
and dynamic γ stimulations on primary and secondary
ending outputs
Glayol Nazari Golpayegani1, Amir Homayoun Jafari1
1Biomedical Engineering Department Islamic Azad University, Science and Research Branch Tehran, Iran
Received 31 October 2008; revised 6 January 2009; accepted 19 January 2009.
ABSTRACT
A linear lumped-parameter mechanical model of
the muscle spindle is presented. It is shown that
the model simulation exhibits the spindle be-
havior in most aspects of transient ramp-stretch
performance. The requirements that such a
model places on the mechanisms of fusimotor
control are discussed. Then the efficacy of
static γ and dynamic γ stimulation on primary
ending output and secondary ending output is
studied. The results of simulations show that
primary ending of muscle spindle is affected
either by static and dynamic stimulation and
Secondary ending of muscle spindle is affected
only by static fiber stimulation. The bias of pri-
mary ending output is increased by an increase
in static γ stimulation. The Ramp of primary
ending response is increased by an increase in
dynamic γ stimulation. An increase in static γ
stimulation in secondary ending of muscle
spindle increases the dc level of secondary
ending output so the bias of output is increased
too.
Keywords: Modeling; Muscle Spindle; Postural Control
Systems
1. INTRODUCTION
The mammalian muscle spindle, as recent anatomical
studies have shown [1,2,3,4,5], is a highly complex sen-
sory organ connected in parallel with skeletal muscles
for detecting change and rate of change in length in
those muscles. Each spindle consists of several “inter-
fusal” fibers (as distinct from “extrafusal” fibers of
which the bulk of skeletal muscle consists) which appear
to fall into two groups, with respect to their anatomical
and their physiological characteristics. A simple example
is illustrated in Figure 1. The larger type of fiber con-
sists of striated contractile tissue with a non contractile
equatorial region which possesses nuclei but lacks myo-
filaments. The distribution of nuclei within the equato-
rial region has led to naming this type the “nuclear-bag
fiber.” The smaller fibers have striations and nuclei
throughout their entire length and are called “nuclear-
chain fibers.”
The efferent innervation to the fibers is by way of the
gamma-motor (γ-motor) or fusimotor system. It is
agreed that there are two anatomically distinct kinds of
fusimotor innervation, distinguishable by the nature of
the nerve endings. There are “γ-plate” fibers, ending in
small end plates similar to those at extrafusal myoneural
junctions and “γ-trail” fibers whose endings are more
diffuse. (There is actually a third kind of innervation, the
β-plate ending, which we will not discuss here). It is not
agreed as to whether both types of endings are found on
both bag and chain fibers, as Barker [1] holds. Accord-
ing to Boyd [2], plates are only found on bag fibers and
trail only on chain fibers.
Activation of skeletal muscle has definite influence in
increasing the stiffness and viscosity of the muscle [7].
In all likelihood, this happens to intrafusal muscles too,
although it has not been verified experimentally. Such
changes in parameter value would modify spindle re-
sponse to stretch.
The amount of force produced by intrafusal contrac-
tion is known only roughly by measurement [8,9] or
computation [10,11], and those measurements are of
whole spindles without differentiation between bag or
chain fiber contraction. Boyd has stated [12,13] that con-
traction is more pronounced and faster in chain fibers
than in bag fibers but much remains to be learned about
this aspect of spindle behavior. The very tentative con-
clusion that has been proposed [14] is that dynamic
stimulation controls output mainly through modification
of parameter values by trail endings, while static stimu-
lation works through force generated in the chain fibers
through the plate endings.
The afferent innervation from the spindles is also of
two types. The primary afferent has its endings both on
the nuclear bag and on the nuclear chain. The secondary

G. N. Golpayegani et al. / J. Biomedical Science and Engineering 2 (2009) 158-165 159
SciRes Copyright © 2009 JBiSE
afferent usually has endings only on the nuclear chain.
When the muscle is stretched or the y-motor nerves stimu-
lated, action potentials are recorded in the primary and
secondary afferent nerves. Corresponding to the anatomi-
cal observations described above, there is an equally bi-
modal response with respect to both stretch and stimulation
as recorded from the two types of nerves.
The purpose of this paper is to describe some simula-
tions of a linear lumped-parameter mechanical model of
the muscle spindle as a neurally controlled transducer of
stretch and discuss the requirements such a model places
on the mechanisms of control. To do this, we shall first
summarize the various types of responses to the various
types of inputs that have been described by numerous
previous investigators [15,16,17,18].
In order to clarify our terminology yet remain rea-
sonably consistent with the physiological literature, let
us define three terms: dynamic sensitivity, static sensi-
tivity, and bias. These refer to steady-state behavior after
transients have died out. The dynamic sensitivity is a
measure of that component of the spindle afferent output
which is proportional to the rate of spindle stretch. It has
units of pps/mm/s. The static sensitivity is a measure of
that component of the spindle afferent output which is
proportional to the amplitude of spindle stretch. It has
units of pps/mm. The bias is the tonic component of the
spindle output that is independent of stretch. It has units
of pps. Note that the bias corresponds to they intercept
on the length-firing rate curve and, as such, it is sensitive
to changes in the slope of that curve. Thus changes in the
static sensitivity may be reflected, in part, by propor-
tional changes in bias.
The γ-motor system can be divided into two groups,
dynamic and static fusimotor fibers, on the basis of
their differential effects on the primary and secondary
afferents. These effects are summarized in Table І. The
primary afferent is influenced by stimulation of both
dynamic an static fibers, the former having their most
pronounced effect on the dynamic sensitivity and the
latter enhancing the bias and static sensitivity. The
secondary afferent is influenced almost solely by the
static fusimotor fibers.
This paper is organized as following sections: we de-
scribe our model in Section 2. We show our simulation
results in Section 3. In Section 4 we study the effects of
static γ and dynamic γ stimulation on primary ending
output and secondary ending output and we have discus-
sion in last section.
2. MODEL
The model we have chosen for our simulation is shown
in Figure 2. It is an extremely general viscoelastic sys-
tem for which we wish to establish, not merely a transfer
function of the spindle, but an anatomical-topological
equivalence such that displacements of the model nodes
give a direct quantitative measure of deformations of the
spindle’s sensory regions.
The upper half of Figure 2 is the nuclear-bag fiber
which consists of a lumped tendon and series elasticity,
two identical contractile sections representing the larger
intrafusal muscle fibers, and a non contractile nuclear
bag from which part of the primary output is taken. The
nuclear chain fiber is the lower half of the figure is at-
Figure 1. Simple two-fiber mammalian muscle spindle with two types of fibers and efferent and afferent innervation.

160 G. N. Golpayegani et al. / J. Biomedical Science and Engineering 2 (2009) 158-165
SciRes Copyright © 2009 JBiSE
Figure 2. Mechanical model of simple mammalian muscle spindle.
tached to the bag fiber at the mid point between the two
contractile sections. It has its own independent
con-tractile section and a non contractile sensory seg-
ment. This segment provides the other portion of the
primary output and all of the secondary output.
Before discussion of our simulations on this system, it
would be of value to consider, in qualitative terms, the
properties of the system that are important in duplicating
spindle behavior. As was pointed out by Crowe and
Matthews [18] and demonstrated in previous simulations
[11,19], the velocity sensitivity of the bag fiber can be
accounted for by assuming that it is considerably stiffer
elastically than the contractile tissue. The chain fiber, on
the other hand, appears fairly uniform in composition. In
terms of the model, it is convenient to talk in terms of a
time constant. This time constant is defined by Eq.1:
iii KBT / (1)
The model response to stretch would be appropriate if
the time constant of the bag T4 were to be much smaller
than that of the muscular segments T1 and T2 while the
two chain time constants T3 and T5 were to be of
equivalent magnitudes to each other.
When stimulation is introduced, the three measures of
spindle response discussed previously, namely, bias,
static sensitivity, and dynamic sensitivity, are useful to
systematize the discussion. Only the contractile seg-
ments are assumed controllable with respect to force
output and parameter changes.
The system may be represented by linear differential
equations as
D
FxxBxxKxxK 



)()()( 21121116  (2)
SD FFxxB
xxBxxKxxKxxK


)(
)()()()(
423
32242332216


(3)
3434322322 )()( xBxKFxxBxxK D 



(4)
4545423423 )()( xBxKFxxBxxK S 



(5)
A set of nonlinear equations in which the elasticities
and viscosities are dependent on length and/or velocity
were deliberately not used because, as we shall show,
almost all the qualitative features of spindle response
can be simulated without the vast increase in computa-
tional complexity required for such a nonlinear model.
An important complicating feature we do require
however, is that the intrafusal muscular components
K1, K2, K3 and Bi, B2, B3 vary with the level of γ
control. In order to avoid the need for time varying
parameters, we restricted the inputs in a manner that
when stretch and fusimotor inputs were both applied
their respective transient responses did not overlap in
time. In this manner, stretch would be applied only
after the parameters had reached appropriate equilib-
rium levels for the degree of fusimotor stimulation.
Since all the experimental data we found in the litera-
ture has been gathered under these same conditions
this limitation is not severe at present.
Under the above constraints, we can take the Laplace
transform of (2) and then rewrite them as in (3) for ana-
log simulation:

G. N. Golpayegani et al. / J. Biomedical Science and Engineering 2 (2009) 158-165 161
SciRes Copyright © 2009 JBiSE
243
2
2
1
11 x
s
F
a
s
x
a
s
x
a
s
x
ax D (6)
49387
65
4
4
3
3
2
2
1
12
xbxb
s
Fs
b
s
F
b
s
x
b
s
x
b
s
x
b
s
x
b
s
x
bx D


(7)
243
3
2
2
13 xc
s
F
c
s
x
c
s
x
cx D (8)
243
4
2
2
14 xd
s
Fs
d
s
x
d
s
x
dx  (9)
We chose to rewrite (7) by combining it with (8)
and (9) and get (10) (equations for ai, bi, ci, di, and ei
in terms of the model parameters are listed in Appen-
dix І):
s
F
e
s
F
e
s
x
e
s
x
e
s
x
e
s
x
e
s
x
ex
S D
765
4
4
3
3
2
2
1
12


(10)
The block simulation of these four Eqs.6, 8, 9, and 10
is shown in Figure 3. The output of Figure 3(c) is
nuclear bag stretch and output of 3(d) is nuclear chain
stretch. The primary output is given by Eq.11 and the
secondary output by Eq.12:
431xxf


 (11)
42 xf

 (12)
3. RESULTS OF SIMULATIONS
Figure 4 shows some results of our simulations for pri-
mary and secondary outputs. The param eters used in the
si
of
4.
SECON-
imulation on primary and secon-
4.1. timu-
increased, 2) the dc level is increased and 3) final with
mulation are listed in Appendix ІІ.
In Figure 4(a) the primary output in response to
stretch and γ stimulation is shown. In the lower curve,
the spindle is relaxed and unstretched for 0.5 second and
then stretched 3 mm at 6 mm/s. The middle curve shows
the effects of adding static γ-motor stimulation of 100
pps starting at t=0 while the upper curve shows the ef-
fects of dynamic γ-motor stimulation of 100 pps. Quite
clearly, dynamic stimulation effects dynamic and static
sensitivity as well as bias by stretching the nuclear bag
and by increasing the viscosity of the bag fiber’s contrac-
tile components. The effects of static stimulation are sim-
ply increased bias and static sensitivity from the chain
branches of the ending. Figure 4(b) shows the output of
the secondary afferent for the same inputs. The absence of
dynamic sensitivity and the ineffectiveness of dynamic
stimulation are apparent. These curves show that our
model does mimic spindle behavior in most aspects
transient ramp-stretch performance as listed in Table 1.
STUDY THE EFFECTS OF STATIC
AND DYNAMIC GAMMA STIMULA-
TION ON PRIMARY AND
DARY ENDING OUTPUTS
After we simulated our model, we studied the effects of
static and dynamic γ st
dary ending outputs.
Effects of Static and Dynamic γ S
lation on Primary Ending Output
As we can see from Figure 4(a), with applying the dy-
namic γ stimulation on primary ending, we have follow-
ing results: 1) the ramp of primary ending response is
Figure 3. Analog computer simulation of model of Figure 2.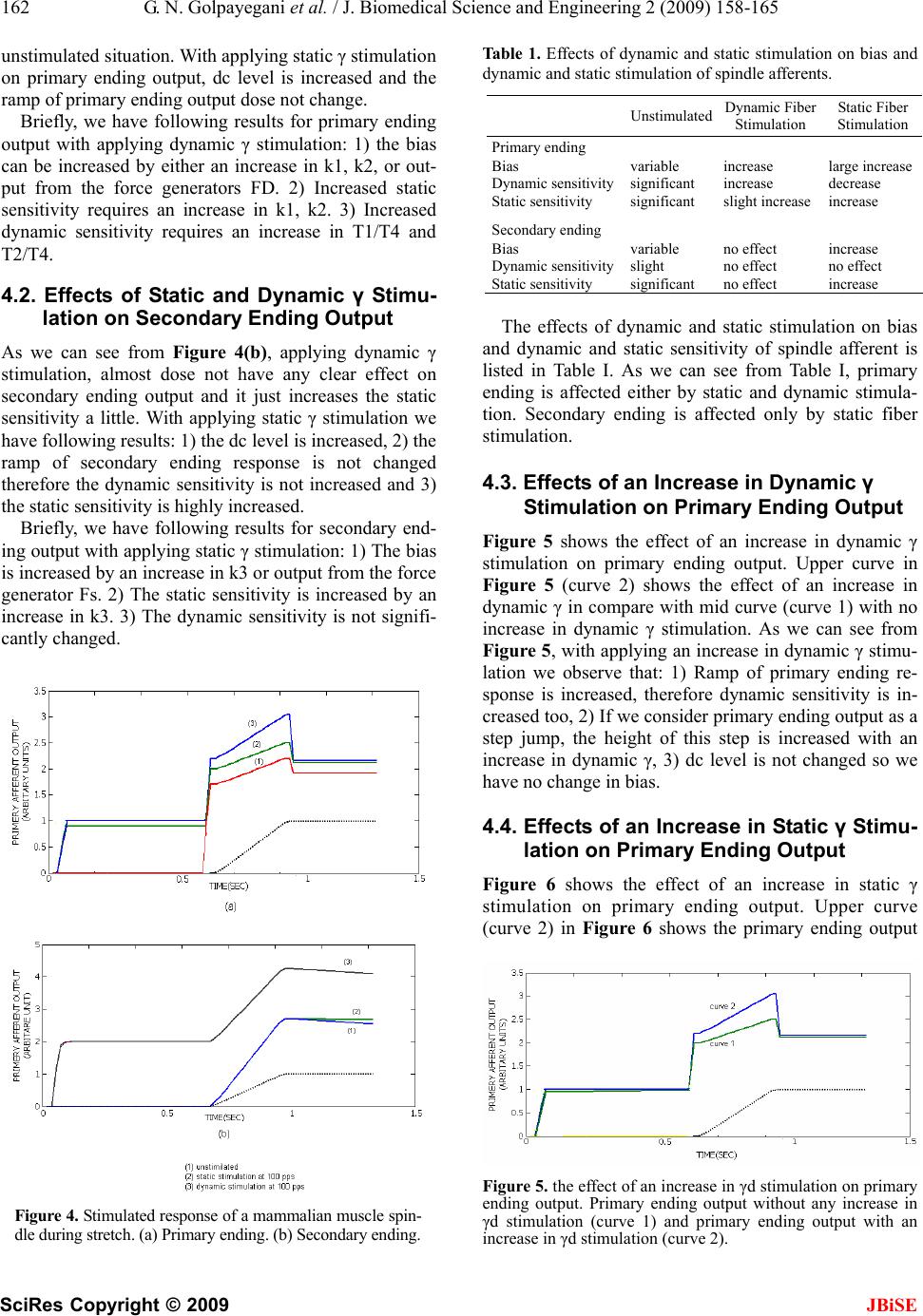

162 G. N. Golpayegani et al. / J. Biomedical Science and Engineering 2 (2009) 158-165
SciRes Copyright © 2009 JBiSE
nstimula
ending
ou
4.2. Effects of Static and Dynamic γ Stimu-
As wic γ
ndary end-
in
uted situation. With applying static γ stimulation
on primary ending output, dc level is increased and the
ramp of primary ending output dose not change.
Briefly, we have following results for primary
tput with applying dynamic γ stimulation: 1) the bias
can be increased by either an increase in k1, k2, or out-
put from the force generators FD. 2) Increased static
sensitivity requires an increase in k1, k2. 3) Increased
dynamic sensitivity requires an increase in T1/T4 and
T2/T4.
lation on Secondary Ending Output
e can see from Figure 4(b), applying dynam
stimulation, almost dose not have any clear effect on
secondary ending output and it just increases the static
sensitivity a little. With applying static γ stimulation we
have following results: 1) the dc level is increased, 2) the
ramp of secondary ending response is not changed
therefore the dynamic sensitivity is not increased and 3)
the static sensitivity is highly increased.
Briefly, we have following results for seco
g output with applying static γ stimulation: 1) The bias
is increased by an increase in k3 or output from the force
generator Fs. 2) The static sensitivity is increased by an
increase in k3. 3) The dynamic sensitivity is not signifi-
cantly changed.
Figure 4. Stimulated response of a mammalian muscle spin-
b le 1 . Effects of dynamic and static stimulation on bias and
d
imulation
dle during stretch. (a) Primary ending. (b) Secondary ending.
ynamic and static stimulation of spindle afferents.
Ta
Unstimulated Dynamic Fiber
Stimulation
Static Fiber
St
Primary ending
Bias
ity gnificant
t
in
crease
rease
l
ecrease
sensitivity
ight
t
o effect o effect
Dynamic sensitiv
sensitivityStatic
variable
si
significan
crease
in
slight inc
arge increase
d
increase
Secondary ending
Bias
Dynamic sensitivity
Static
variable
sl
significan
no effect
n
no effect
increase
n
increase
dd mulabias
n
lis
namic γ
ut
crease in Static γ Stimu-
stimur curve
The effects of ynamic anstatic stition on
ad dynamic and static sensitivity of spindle afferent is
ted in Table І. As we can see from Table І, primary
ending is affected either by static and dynamic stimula-
tion. Secondary ending is affected only by static fiber
stimulation.
.3. Effects of an Increase in Dy4
Stimulation on Primary Ending Outp
Figure 5 shows the effect of an increase in dynamic γ
stimulation on primary ending output. Upper curve in
Figure 5 (curve 2) shows the effect of an increase in
dynamic γ in compare with mid curve (curve 1) with no
increase in dynamic γ stimulation. As we can see from
Figure 5, with applying an increase in dynamic γ stimu-
lation we observe that: 1) Ramp of primary ending re-
sponse is increased, therefore dynamic sensitivity is in-
creased too, 2) If we consider primary ending output as a
step jump, the height of this step is increased with an
increase in dynamic γ, 3) dc level is not changed so we
have no change in bias.
4.4. Effects of an In
lation on Primary Ending Output
Figure 6 shows the effect of an increase in static γ
lation on primary ending output. Uppe
(curve 2) in Figure 6 shows the primary ending output
Figure 5. the effect of an increase in γd stimulation on primary
ending output. Primary ending output without any increase in
γd stimulation (curve 1) and primary ending output with an
increase in γd stimulation (curve 2).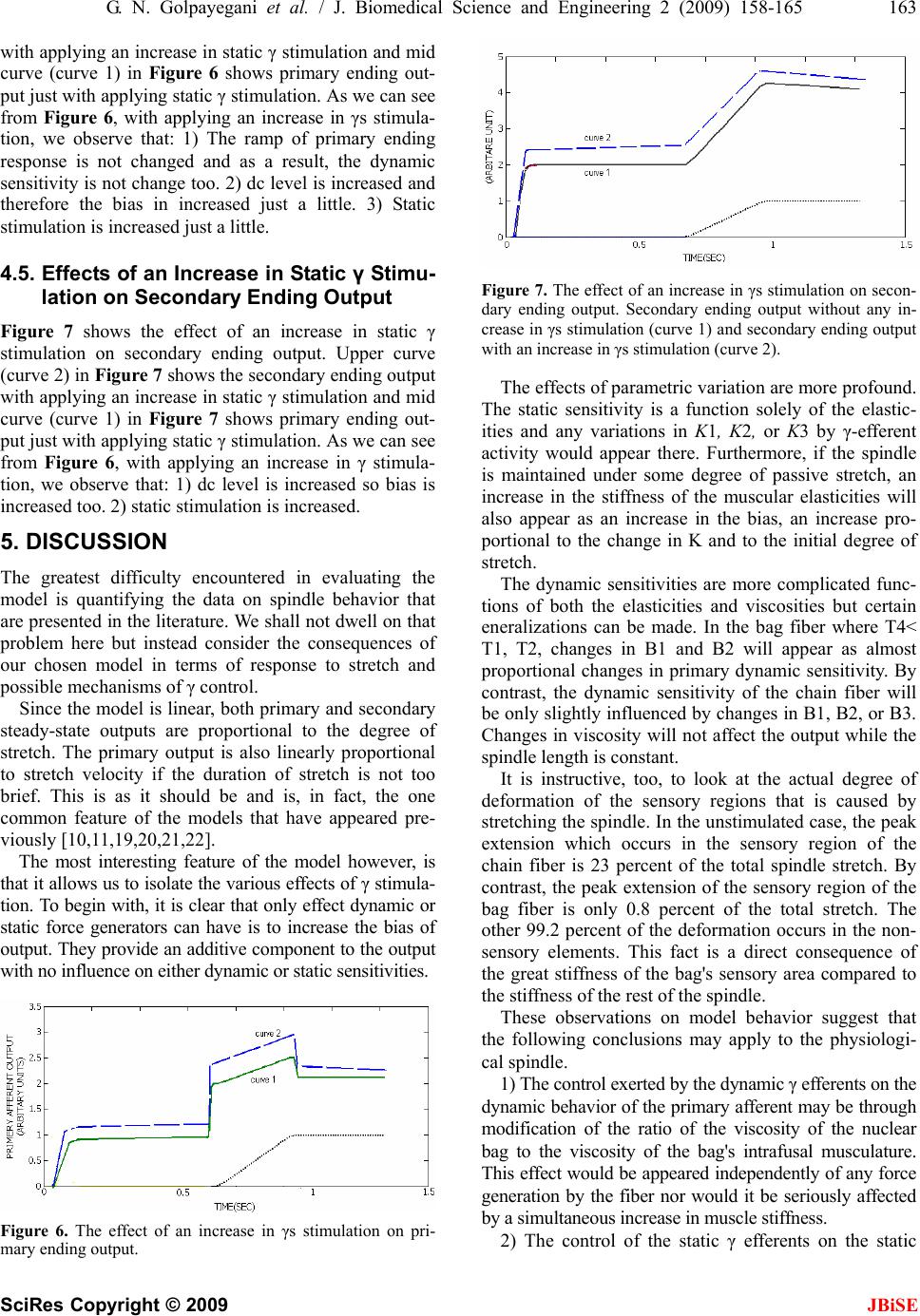

G. N. Golpayegani et al. / J. Biomedical Science and Engineering 2 (2009) 158-165 163
SciRes Copyright © 2009 JBiSE
Static γ Stimu-
Figu ic γ
encountered in evaluating the
with applying an increase in static γ stimulation and mid
curve (curve 1) in Figure 6 shows primary ending out-
put just with applying static γ stimulation. As we can see
from Figure 6, with applying an increase in γs stimula-
tion, we observe that: 1) The ramp of primary ending
response is not changed and as a result, the dynamic
sensitivity is not change too. 2) dc level is increased and
therefore the bias in increased just a little. 3) Static
stimulation is increased just a little.
.5. Effects of an Increase in4
lation on Secondary Ending Output
re 7 shows the effect of an increase in stat
stimulation on secondary ending output. Upper curve
(curve 2) in Figure 7 shows the secondary ending output
with applying an increase in static γ stimulation and mid
curve (curve 1) in Figure 7 shows primary ending out-
put just with applying static γ stimulation. As we can see
from Figure 6, with applying an increase in γ stimula-
tion, we observe that: 1) dc level is increased so bias is
increased too. 2) static stimulation is increased.
5. DISCUSSION
The greatest difficulty
model is quantifying the data on spindle behavior that
are presented in the literature. We shall not dwell on that
problem here but instead consider the consequences of
our chosen model in terms of response to stretch and
possible mechanisms of γ control.
Since the model is linear, both primary and secondary
steady-state outputs are proportional to the degree of
stretch. The primary output is also linearly proportional
to stretch velocity if the duration of stretch is not too
brief. This is as it should be and is, in fact, the one
common feature of the models that have appeared pre-
viously [10,11,19,20,21,22].
The most interesting feature of the model however, is
that it allows us to isolate the various effects of γ stimula-
tion. To begin with, it is clear that only effect dynamic or
static force generators can have is to increase the bias of
output. They provide an additive component to the output
with no influence on either dynamic or static sensitivities.
Figure 7. The effect of an increase in γs stimulation on secon-
y ending output without any in-
ore profound.
h
dary ending output. Secondar
crease in γs stimulation (curve 1) and secondary ending output
with an increase in γs stimulation (curve 2).
The effects of parametric variation are m
Te static sensitivity is a function solely of the elastic-
ities and any variations in K1, K2, or K3 by γ-efferent
activity would appear there. Furthermore, if the spindle
is maintained under some degree of passive stretch, an
increase in the stiffness of the muscular elasticities will
also appear as an increase in the bias, an increase pro-
portional to the change in K and to the initial degree of
stretch.
The dynamic sensitivities are more complicated func-
tions of both the elasticities and viscosities but certain
eneralizations can be made. In the bag fiber where T4<
T1, T2, changes in B1 and B2 will appear as almost
proportional changes in primary dynamic sensitivity. By
contrast, the dynamic sensitivity of the chain fiber will
be only slightly influenced by changes in B1, B2, or B3.
Changes in viscosity will not affect the output while the
spindle length is constant.
It is instructive, too, to look at the actual degree of
deformation of the sensory regions that is caused by
stretching the spindle. In the unstimulated case, the peak
extension which occurs in the sensory region of the
chain fiber is 23 percent of the total spindle stretch. By
contrast, the peak extension of the sensory region of the
bag fiber is only 0.8 percent of the total stretch. The
other 99.2 percent of the deformation occurs in the non-
sensory elements. This fact is a direct consequence of
the great stiffness of the bag's sensory area compared to
the stiffness of the rest of the spindle.
These observations on model behavior suggest that
the following conclusions may apply to the physiologi-
cal spindle.
1) The control exerted by the dynamic γ efferents on the
dynamic behavior of the primary afferent may be through
modification of the ratio of the viscosity of the nuclear
bag to the viscosity of the bag's intrafusal musculature.
This effect would be appeared independently of any force
generation by the fiber nor would it be seriously affected
by a simultaneous increase in muscle stiffness.
2) The control of the static γ efferents on the static
Figure 6. The effect of an increase in γs stimulation on pri-
mary ending output.

164 G. N. Golpayegani et al. / J. Biomedical Science and Engineering 2 (2009) 158-165
SciRes Copyright © 2009
e, in part,
m
eration but the existence of this co
is
o
re
al fibers are accept-
ab
are
no
2) The motor ininervation of the
cle spindle, in Nobel Symposium
postural control systems, part 1: torque disturbance input,
[8] ff, (2001) Tension development by isolated
n
L. Gottlieb, and L. Stark, (March 2004)
tlieb, G. C. Agarwal, and L. Stark, (March 2003)
vior of isolated mammalian
echanical properties of mammalian
static
u, Y. Laporte, and B. Pages, (2001) Similitude
) Action
001)
fects of
k, (2001) A model of
n, G. Lennerstrand, and U. Thoden, Cat
fuseau
alian
behavior of the two types of afferents may b6, 116-121.
K. Diete-Spi
odification of the elasticities of either the bag or the
chain but may include a large degree of output from the
forcegenerators.
3) The control of bias by the γ efferents may be by in-
trafusal force genntrol changes in crayfish stretch receptors, J. Physiol.
(London), 159.
[10] G. C. Agarwal, G.
muscle spindles of the cat, J. Physiol. (London), 193.
[9] K. Krnjevk and N. M. Van Gelder, (2002) Tensio
open to question because changes in static sensitivity
can appear as change in the bias of a stretched spindle.
4) The question of whether the bag fiber contracts in
response to dynamic γ stimulation will be difficult t
Models of muscle proprioceptive receptors, presented at
the University of Michigan-NASA Conf. Manual
Control.
[11] G. L. Got
solve by direct visual observation because the bag is
very stiff and deforms only slightly.
5) In light of the above, either of the theories of
y-efferent innervation of the intrafus
Stretch receptor models, part I single-efferent
single-afferent innervation, IEEE Trans. Man-Machine
Systems, MMS-10, 17-27.
[12] A. Boyd, (2001) The beha
le. Even if both plate and trail endings are to be found
on both bag and chain fibers, the distinguishing response
of the bag fiber would be to only one type (the paramet-
ric modifier, presumably the trail ending) while the chain
could respond to either or both types of innervation.
6) We should also recognize the fact that the dynamics
displayed by the spindle and mimicked by the model
muscle spindles with intact innervation, J. Physiol.
(London), 186.
[13] (2001) The m
intrafusal muscle fibers, J. Physiol. (London), 187.
[14] P. Bessou and Y. Laporte, (2001) Observations on
fusimotor fibres, in Nobel Synmposium-Muscular
Afferents and Motor Control, R. Granit, Ed. New York:
Wiley.
[15] P. Besso
t really sufficiently complex to require a fourth-order
transfer function. The purpose of this elaborate model
we have presented is to maintain an equivalence between
the spindle anatomy and the model topology, but as a
black box, simpler models presented previously [10,11],
are quite adequate.
REFERENCES
des effets (statiques ou dynamiques) exerces par des
fibres fusimotrices le chat, J. Physiol, Paris, 58.
[16] B. Appelberg, P. Bessou, and Y. Laporte, (2001
of static and dynamic fusimotor fibres on secondary
endings of cats’ spindles, J. Physiol. (London), 185.
[17] E. Emonet-Denand, Y. Laporte, and B. Pages, (2
JBiSE
[1] D. Barker, (200
mammalian mus stim
Muscular Afterents and Motor Control, R. Granit, Ed.
New York: Wiley.
[2] A. Boyd, (1996) The motor innervation of mammalian
muscle spindles, J. Physiol. (London), 159.
[3] R. W. Banks, (2001) The tenuissiumus muscle of the cat,
J. Physiol. (London), 133.
[4] D. Barker (1999) The innervation of mammalian
neuro-mulscular spindles, J. Physiol. (London), 140.
[5] (2000) Simple and compound mammalian muscle
spindles, J. Physiol. (London), 145.
[6] D. Barker and I. A. Boyd, (2004) in Nobel Symposium
Muscular Afferents and Motor Control, R. Granit, Ed.
New York: Wiley.
[7] G. C. Agarwal, B. M. Berman, and L. Stark, Studies in
Fibres fusimotrices statiques et fibres fusimotrices
dynamiques chez le lapin, Arch. Ital. Biol., 104.
[18] Crowe and P. B. C. Matthews, (2003) The ef
ulation of static and dynamic fusimotor fibres on the
response to stretching of the primary endings of muscle
spindles, J. Physiol. (London), 174.
[19] J. C. Houk, R. Cornew, and L. Star
adaptation in amphibian spindle receptors, J. Theoret.
Biol., 12.
[20] Anndersso
muscle spindle model, Dig. 1999 Internatl. Conf. on
Medical and Biological Engineering (Stockholm).
[21] M. D. Angers, (2001) Model mecanique de
neuromusculaire de-efferente: Terminaisons primaires et
secondaires, Compt. Rend. Acad. Sci. (Paris), 261.
[22] Crowe, (2003) A mechanical model of the mamm
muscle spindle, J. Theoret. Biol., 21.

G. N. Golpayegani et al. / J. Biomedical Science and Engineering 2 (2009) 158-165 165
SciRes Copyright © 2009 JBiSE
PPENDIX 1
ns relate the block simulation pa-
A
The following equatio
rameters (Figure 3) to the model parameters (Figure 2)
as determined by (3) and (4).
1) a parameters:
1
1
2
1
61
1,B
K
a
B
KK
a


1
4
1
6
3
1
,B
a
B
K
a
2) c parameters:
42
2
2
42
2
1,BB
K
c
BB
B
c 


42
4
42
42
3
1
,BB
c
BB
KK
c 



3) d parameters:
33
12
35 35
35
34
35 35
,
1
,
BK
dd
BB BB
KK
dd
BB BB



 

4) e parameters:
HKe 61 
H
BB
KB
BB
KB
e









53
35
42
24
2
H
BB
KBKB
eH
BB
KBKB
e

















53
5335
4
42
4224
3,
H
BB
B
eHKe 







42
4
665 ,
H
BB
B
e







53
5
7
where
53
53
42
42
1
BB
BB
BB
BB
H




PPENDIX 2
meter values were used in the
A
The following para
simulation shown in Figure 4:
25.002.0 11


BK
025.002.0 22


BK
001.003.0 33


BK
01.00.4 44


BK
001.003.0 55


BK
0.2
6

K
dynamic

firing rate

D
f

S
fstatic

firing rate
0003.0,0003.0 





S
S
D
Df
F
f
F
01.0
2121 











DDDD f
B
f
B
f
K
f
K
01.0
33 





SS f
B
f
K
30/



(see(5)), K is given in N/m and B in N·s/m