 Advances in Historical Studies 2014. Vol.3, No.1, 56-67 Published Online February 2014 in SciRes (http://www.scirp.org/journal/ahs) http://dx.doi.org/10.4236/ahs.2014.31006 Open Access Integrating Chemistry, Electricity and Magnetism into Dynamical Natural Philosophy: J. F. Fries’s Extension of Kant’s Metaphysical Foundations Erdmann Görg Institut für Philosophie I, Ruhr-Universität, Bochum, Germany Email: erdmann.goerg@rub.de Received August 12th, 2013; revi s ed September 13th, 2013; accepted September 20th, 2013 Copyright © 2014 Erdmann Görg . This is an open access article distribu ted under the Creative Co mmons Attri- bution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Erdmann Görg. All Copyright © 2014 are guarded by law and by SCIRP as a guardian. Kant’s Metaphysical Foundations of Natural Science has an almost exclusive focus on Newton’s Philo- sophiae Naturalis Principia Mathematica. Other research fields like electrostatics, magnetism, chemis- try or biology are hardly dealt with. A successor of Kant, the philosopher, natural scientist and mathema- tician Jakob Friedrich Fries (1773-1843), accommodates Kant’s major thoughts on a metaphysical foun- dation but aims at assisting natural science of his time by employing a heuristic interpretation of Kant’s fundamental forces. In my paper, I will trace Fries’s application of his heurist maxims on the development of other evolving fields of research. This will provide concrete examples on how Fries thought philosophy to support science. For that reason, I will highlight the different status that Kant and Fries concede non- mechanic research areas. To restrict the analysis, I will focus on the actual incorporation of chemical dis- solution, Coulomb’s law and magnetism into Kantian Dynamics as a concrete example of Fries’s method- ology. Keywords: Fries; Kant; Newtonianism; Natural Philosophy; Metaphysical Foundations of Natural Science; Mathematical Philosophy of Nature; Mechanics; Electricity; Magnetism; Chemistry Introduction: Mathematical Philosophy of Nature, the Amory of Natural Science Right at the beginning of his Mathematical Philosophy of Nature, Fries declares: Namely, this Science [The Mathematical Philosophy of Nature] is the armory of all those hypotheses from which we derive the explanation of later experience. By far the most therein is of mathematical development, but the fundamental concepts are philosophical, and if it would work out to convince natural scientists of this, the disci- pline of hypotheses would profit greatly from this (Fries, 1979: p. 10)1. How does this “arming” of natural science by the Mathe- matical Philosophy of Nature take place? Natural science is in need of experience, mathematics, and philosophy. Sheer col- lecting of empirical data does not lead to an explanation. It just allows a “mere induction”, as Fries calls it, in contrast to a “ra- tional induction”. Fries gives an example from electrostatics: Further, if we claim: Same-named electricities repel each other, non same-named elect rici ties a ttract e ach oth er, t hat is a matter of mere induction. But if we assume luminous fluids as cause of this repulsion and attraction, we now try an explanation which is rooted in pure theory. The same difference will apply to an investigation of the appearances of magnetism, heat, light and several others. […] [T]he development of the doctrine of nature will just then always approach its completeness if we luckily can apply such a ground of explanation from pure theory and thereby find the beginning of a constitutive theory (Fries, 1979: pp. 612-613). A rational induction, like the explanation of Coulomb’s law above, is in need of leading maxims. The development of such maxims is one of the main tasks of the Mathematical Philoso- phy of Nature2. This paper aims to provide a more thorough understanding of Fries’s idea of the necessity of an interplay between natural philosophy and natural science by investigating how Fries accomplished such an application of natural phi- losophy onto the research areas of his time. To do so, I will 1The follo wing quotations ar e translated by the au thor. The emphases g iven in the quotations fol l ow the German original texts. “Our whole metaphysical-mathematical pure theory with all its consti - tutive developments is only about to completely exhibit those guiding ma x - ims for the empirical sciences from which the induction of exper i ence can retrieve natural laws and guess the hypothesis of its gr ounds of explanation.” (Fries , 1979: p. 615). For a closer look on the mechanism of the interplay of rational induction and leading maxims cf. Fries 1967, vol. 2, pp. 310 - , 1971a: pp. 123-124, Fries, 1971b: pp. 334-340. For accounts con Fries’s heuristic, cf. e.g. van Zantwijk, 2009, 2010, Herrmann, 2000 -83. Herrmann, 2012: pp. 28-44.  E. GÖRG Open Access consider his approach of integrating chemistry3, electrostatics and magnetism into Kant’s constitutive theory. Fries’s approach relies on an extension and revision of Kant’s natural philosophy. It will therefore be necessary to give an overlook of Kant’s Metaphysical Foundations of Natural Science and its focus on Newton’s Philosophiae Naturalis Principia Mathematica4, because these are Frie s’ s starting points5. This will be exemplified by an analysis of Kant’s dynamics. Then I’ll focus on the relation between the Mathematical Philosophy of Nature and the Metaphysical Foundations of Natural Science as well as on Fries’s further elaboration in the chapter on dynamics. Concluding, I will concentrate on the above mentioned examples as a concrete application. Fries’s Starting Point: Kant’s Metaphysical Foundations Fries saw himself as a Kantian6. For an understanding of his natural philosophy it is necessary to first look into the philoso- phy of Kant. This will enable us to highlight the changes in Fries’s extension of Kant’s philosophy. Building a Metaphysical Basis for Newtonian Mechanics The strong impact of Newton’s Mechanics can be found throughout several parts of Kant’s work. Newton and his Prin- cipia were paradigmatic for Kant’s view on science in general7. The references to Newton that can be found in the writings of Kant are legion. One of the most important texts which shows the great influence of Newton on Kant is the Metaphysical Foundations of Natural Science. This book is intended as a concrete application of the critical philosophy of the Critique of Pure Reason onto the basis of natural science8. Kant does not criticize the mathematical achievements of Newton’s physics but rather the epistemological status he ascribes to his findings9. Newton, in support of the Royal Society and against Descartes, pretends10 to have a very empirical methodology11, whereas Kant underlines that an empirical foundation is not sufficient. He believes that Newton overlooks that central results of the Principia can be derived a priori from critical philosophy. Hence all natural philosophers who have wished to pro- ceed mathematically in their occupation have always, and must always have, made use of metaphysical principles (albeit unconsciously), even if they themselves solemnly guarded against all claims of metaphysics upon their sci- ence. Undoubtedly they have understood by the latter the folly of contriving possibilities at will and playing with concept, which can perhaps not be presented in intuition at all, and have no other certification of their objective re- ality than that they merely do not contradict themselves. All true metaphysics is drawn from the essence of the fa- culty of thinking itself, and is in no way fictitiously in- vented on account of not being borrowed from experience. Rather it contains the pure actions of though, and thus a priori concepts and principles, which first bring the mani- fold of empirical representations into law governed con- nection through which it can become empirical cognition, that is, experience. Thus these mathematical physicists could in no way avoid metaphysical principles, and, among them also not those that make the concept of their proper object, namely matter, a priori suitable for applica- tion to outer experience, such as the concept of motion, the filling of space, inertia, and so on (Kant, 2004: pp. 8-9)12. This passage is fundamental for a thorough understanding of the Metaphysical Foundations of Natural Science. A doctrine, if it is to gain scientific status, needs an a priori basis. This can be illustrated by Kant’s different treatment of physics and che- mistry in the preface to the Metaphysical Foundations of Natu- ral Science. As Kant makes clear in his chapter on archi- tec- tonic, the structure of science is fixed by an idea of reason that gives it an a priori structure to which the empirical has to be subordinated13. This structure makes the difference between mere doctrine and science. Proper natural science in contrast to “improperly so called natural science” (Kant, 2004: p. 4)14 is based on a priori derivable laws15. The principles of chemistry have only the status of empirical laws. The major laws of phys- It will lat er become clear that Fr ies tried hard to in tegrate chemis try into a dynamic matter -theory. In his publications ther e are many more elaboratio ns on chemistry than on electrostatics or magnetism. Co n cerning chemistry, this paper will focus only on Fries’s revision of Kant’s theory of chemical diss olution. He writes: “The specific topic of chemistry, as a part of experime ntal phys process , i.e. the mutual diffusion of different bodies, which takes place as so on as they co me in cont act with each other an d after whi ch these bodies engage the same space together” (Fries , 1974: p. 322). In the following, Newton’s Philosophiae Naturalis Principia Mathematica is simply referred to as the Principia. cf. e.g. Friedman, 1992: p. 136. “For all this, I remain a Kantian […].” (Fries, 2011 : p. 808). cf. Friedman, 1992: p. 136. cf. Kant, 2004: p . 13. MFN, 478 and Kant, 1929: p. 14. CpR, A XXI. Addi - date system, references to Kant’s writings are made by naming a shortform of the title, volume and page of the Akademieaus gabe as well. Ex cluded ar e references t o the Critique of Pure Reason refer to the paging of the original edition. The Critique of Pure Reason is thereby short CpR, the Meta ph ysical Fou ndations of Natural Science as MFN, as OP, Monadologia Physica as MoPh, New Theory of Mo as NTMR, and the Universal Natural History and Theory of Heaven as UTH. He thereby f ocuses on the s tatus of their v alidity, not the gen esis of physi - cal theor ies themselv es. Kant leaves no doubt that the fin ding, for examp le, of the laws of motion can be done easier by empirical investigation than by metaphysics. cf. Kant, 2004: p. 13. MFN, 4, 477. The great influence of metaphysical and theological ideas on New ton’s System, wh ich I will n ot discuss her e, becomes apparen t by his early writ De Gravitatione (Newton, 2004), the Scholion Generale of the Prin (Newton, 1999: pp. 939-944), the Query 31 of his Opticks (Newton : pp. 350-382) and the Correspondence of his pupil Sam uel Clarke with Gottfried Wilhelm Leibniz (Clarke, 1717). e.g. Newton, 1999: pp. 795-796 and p. 943, and Newton, 1730: p. 344. MFN, 4, 472 (cf. as well Kant, 1929: p. 663. CpR, 849/877). wton is not named, it is clear that Kant refers to him (cf. Friedman, 1992 ; Pollok, 1997: p. 128). The reference to Newton, besides other points can be seen by the characterisation of Newton’s critique on metaphysics. The “fictitiously invention” for sure is a hint at Ne w ton’s “hypothesis non fingo” (Newton , 1726: p. 530). “The whole is thus an organized unity (articulatio), and not an aggre coacervatio). It may grow from within (per intussusception ), but not by external addition ( per appositionem ). It is thus like an animal body, the growth of which is not by the addition of a new member, but by the render - ing of member, without change of proportion, stronger and more effective for its purpose.” (Kant, 1929: pp. 653-654. CpR, 833/ 861). MFN, 4, 468. Kant 2004, p. 4. MFN, 4, 468.  E. GÖRG Open Access ics, in contrast, can be derived a priori. This special metaphys- ics is deduced from the system of pure reason by the applica- tion of general metaphysics on to the concept of matter. The a priori status of “proper science”16 goes hand in hand with the need of its mathematization, a thought later adopted and ad- vanced by Fries. I assert, however, that in any special doctrine of nature, there can be only as much proper science as there is ma- thematics therein (Kant, 2004: p. 6)17. While philosophy operates discursively, mathematics con- structs concepts in intuition18. The concepts in natural philoso- phy need intuition because without a representation they are in danger to be inconsistent19. Natural science, according to Kant’s definition, needs to have an a priori part, the underlying concepts need to be constructed a priori20. This a priori con- struction in intuition is mathematics. In contrast to physics, chemistry cannot live up to this claim. Kant writes: So long, therefore, as there is still for chemical actions of matters on one another no concept to be discovered that can be constructed, that is, no law of the approach or withdrawal of the parts of matter can be specified accord- ing to which, perhaps in proportion to their density or the like, their motions and all the consequences thereof can be made intuitive and presented a priori in space (a demand that will only with great difficulty ever be fulfilled), then chemistry can be nothing more than a systematic art or experimental doctrine, but never a proper science, because its principles are merely empirical, and allow of no a pri- ori presentation in intuition. Consequently, they do not in the least make the principles of chemical appearances conceivable with respect to their possibility, for they are not receptive to the application of mathematics (Ka nt, 2004: p. 7)21. For the metaphysical foundation of physics, more precisely mechanics, the concept of matter must be determined by the categories of the Critique of Pure Reason22. The relation of general and special metaphysics is the following: On the one hand, a proper metaphysical foundation of science is in need of critical philosophy because it is an application of the synthetic principles of pure understanding and the categories of the Cri- tique of Pure Reason on the fundamental concept of natural science, matter. On the other hand23, the Critique of Pure Rea- son is as well in need of the Metaphysical Foundation of Natu- ral Science as a concrete illustration24. Besides this, an integra- tion of mechanics, in the sense of Newton’s Principia, into critical philosophy would be a great success for it would pro- mote critical philosophy. Corresponding to the four types of categories, the Metaphy- sical Foundations of Natural Science consist of four chapters. Phoronomy makes the application of mathematics possible by giving rules of the construction of moving bodies. Here matter is seen as merely punctual. Dynamics takes a look at matter as something extended. Here Kant tries to establish the two fun- damental matter constituting forces of attraction and repulsion. The third chapter, named mechanics, tries to derive three fun- damental laws of physics, whereby two of them can be found in Newton’s Principia. And lastly, phaenomenology which trans- forms movement from “appearance” into “experience”. Fries’s above-mentioned opening to new research is mainly done by a revision of Kant’s dynamics. For that reason we shall investigate this second chapter of the Metaphysical Founda- tions of Natural Science and its closeness to Newtonian me- chanics. A Closer Look at Kant’s Focus on Newton Exemplified by His Dynamics Besides the title of the Metaphysical Foundations of Natural Science25 and numerous links to Newton’s works in the text26, Kant’s Newtonianism becomes clear by the text’s content itself. The first, third and the last chapter include a revised version of Newton’s views on absolute space. The mechanics present two of three Newtonian laws of motion, derived from an application of the analogies of experience of the Critique of Pure Reason- ing onto the concept of matter27. Phaenomenology deals with Kant, 2004: p. 4. MFN, 4, 468. MFN, 4, 470. Kant, 1929: pp. 578-580. CpR, 716-719/744-747. Not in a lo g i cal s ense, since s ynthetic a p r i o r i can be derived only wi th the support of intuition (cf. Kant , 2004: pp. 191-192. CpR, 154/193). “Now to cognize something a priori means to cognize it from its mere possibility. But the possibility of determinate natural things cannot be co g- nized from their mere concepts; for from these possibility of the thought (that it does not contradict itself) can certainly be cognized, but not the possibility of the object, as a natural thing that can be given outside the thought (as existing). Hence, in order to cogni ze the possibility of deter mi- nate natural things, and thus to cognize them a priori, it is still required that the intuition correspond ing to the concept be given a priori, th at is, that the concept be constructed. Now rational cognition through construction of concepts is m athematical.” (Kant, 2004: p. 6. MFN, 4, 470). cf. Kant, 1929: p. 93. CpR, 51/75. Kant, 2004: p. 7 . MFN, 4, 470-471 (cf. as well Kant, 2004: p. 4. M FN , 4, 468). Furthermore, against the declaration of the architecton ic chap Critique of Pure Reason (and other documents such as Kant’s letter to Schütz (Kant , 1922: p. 406)) the Metaphysical Foundations of Natural Science do not deal with the metaphysical foundations of physi ology as a whole, that means rati o n al physics and ps ychology (cf . K an t , 1929: pp. 662- CpR 845-847/873-875). The critique of the possibility of psy chology as science i s tied to Kant’s attack on chemistry, b ut exceeds it. An applic a- tion of mathematics to our inner sense would imply both a separation of the contents of o ur inner obser vation as well as a synthesis of its parts. This, however, is impossible according to Kant. Our inner sense cannot be de m- onstrated, that is why a foundation a priori is impossible and is not dealt with in the Metaphysical Foundations of Natural Science (cf. Kant, 2004 -8. MFN, 4, 471). cf. Kant, 2004: pp. 10-12. MFN, 473-477. The interdependency is stressed by Plaaß, 1994: pp. 211-212. 24“It is also i ndeed very r emar kab le ( but cann ot be expo unded in detai l h ere) that gen eral metaphysics , in all ins tances where i t requires examples (i ntu i- tions) in order to provide meaning for its pure concepts of the understanding must always take them from the general doctrine of body, and thus from the form and principles of outer intuition; and, if these are not exhibited com- pletely, it gropes uncertainly and unsteadily mere meaningless concepts.” (Kant , 2004: p. 13. MFN, 4, 478). Gloy, with reference to Heidegger, 1962 and Plaaß, 1994: p. 214 points out that the Metaphysical Foundations of Natural Science were pub years aft er the Principia (Gloy, 1976: p . 176, cf. as well Po llok, 1997). Moreov er, Gl oy i nterp ret s th e tit le as a po lemic ag ain st th e ti tl e of Ne w ton’s main work. Even though the author of this text would not go as far in his inte rpretation to see it as polemic, the direct reference to the Principia is obvious. This can also be seen in the Opus Postumum in which Kant speaks about Newton’s main work as the “ Mathematical Foundations of Natural Scie nce” (for instance Kant, 1938: p. 161. OP, 161. cf. Pollok, 1997: p. XXX IX). 26Newton is named more than every other person in the text and nearly as often as all other persons combined. Newton’s second law is missing in the Metaphysical Foundations of Na (the change of motion is proportional to the impressed force). Instead, Kant formulated the conservation of the quantity of ma tter (Kant : p. 76. MFN, 4, 537). Concerning an exposure of different interpret a- tions f or t hi s no t i ceable varian ce cf . P ulte, 2005: pp. 233-236 and Bo n : pp. 86-87.  E. GÖRG Open Access different modalities of motion, whereby the different denota- tions are adopt from the scholion about time, space, place and motion from the Principia. The revision of fundamental New- tonian concepts shall here be shown by a look at Kant’s dy- namics, the chapter whose extension by Fries has crucial meaning to his accommodation of chemistry, electrostatics and magnetism. Kant’s assimilation of attraction as a matter-con- stituting fundamental force in the dynamics can be seen as a reversion of Newton’s gravity. The dynamics, like all chapters, starts with an explication: Matter is the movable insofar as it fills a space. To fill a space is to resist every movable that strives through its motion to penetrate into a certain space (Kant, 2004: p. 33)28. This resistance is the resistance against another invading body. It is possible not because of its mere existence but be- cause of two matter constituting forces29. Kant explains these fundamental forces as follows: Attractive force is the moving force by which a ma tter can be cause of the approach of others to it (or, what is the same, by which it resists the removal of others from it). Repulsive force is that by which a matter can be the cause of others removing themselves from it (or, what is the same, by which it resists the approach of others to it). (Kant, 2004: p. 35) 30. According to Kant, no other moving forces are possible. These fundamental forces are not properties of matter. Rather, they mak e matter as some thing that fills space possible. Repulsion is a force that acts on bodies in contact. It is thereby increasing proportionally to its density (or inverse pro- portional to its volume). Matter can therefore never be pene- trated but only compressed to any finite degree by another body31. Kant’s dynamical conception of matter is thereby op- posing a mathematical filling of space, that means an absolute impenetrability. Apart from the force of repulsion, another fundamental force is necessary, the force of attraction. Otherwise the density of matter would decree under every arbitrary limit and matter would suspend. While the force of attraction makes the exis- tence of matter possible, the attractive force cannot itself rely on a material medium. It is thereby attracting other bodies as action at a distance: The attraction essential to all matter is an immediate ac- tion of matter on other matter through empty space. (Kant 2004, p. 50).32 And: The original attractive force, on which the very possibility of matter as such rests, extends immediately to infinity throughout the universe, from every part of matter to every other part (Kant 2004, p. 55)33. This description of attraction is heavily influenced by New- ton’s universal law of gravitation34. Newton was very cautious in his statements on the nature and causes of gravity35. Fur- thermore, he saw inertia instead of gravity essential to bodies36. In ascribing gravity the role of a matter-constituting fundamen- tal force and by denying the existence of an inertial force, Kant gives it the place that he believes it deserves in physics37. The narrowing to a metaphysical foundation of the Principia be- comes thereby clear because of the denial of the possibility of other fundamental forces: Only these two moving forces of matter can be thought. For all motion that one matter can impress on another, since in this regard each of them is considered only as a point, must always be viewed as imparted in the straight line there are only to possible motions: the one through which the two points remove themselves from one another, the second through which they approach one another. (Kant, 2004: p. 35)38. So the search for the fundamental forces ends with the Meta- MFN, 4, 496. In his remark to the first explanation, Kant underlines t hat he does not mean the resistance towards a change of motion, but a resi s tance when the volume of a body is decreased (cf. Kant , 2004: pp. 33-34. MFN, 4, 496- 497) His intention is to highlight the di f ference between repu lsion and attr action on one side and an iner tial force on the other. As Kant underlines in the third chapter, i nertia mean s just the “ lifeles sness” (cf. K ant, 2004: p. 83. MFN , 4, 544) of matter. The uniform m o tion of a body is not caused by an inherent force. This is clearly a statement against Newton. Kant is thereby heavily influenced by Euler’s Cart esianism. Kant adopted Euler’s refuse of an inherent force (cf. f.i. Euler , 1765: , 1802: vol. 1, pp. 263- 274) between the years 1756 and 1758 (cf. Pollok , 2000: p. 385). It is very rem ark abl e th at in th e Mo nadologia Physica Kant deri ves the force of iner tia (Kant , 1900a: p. 485. MoPh , 1, 48 5), wh e- reas he denies its existence in his New Theory of Motion and Rest (Kant : pp . 19-21. NTMR, 2 , 19-21). A likel y reason for this may be his rea Mechanica (Euler, 1736) between these publications. MFN, 4, 498. cf. Kant, 2004: p. 37. MFN, 4, 501. Important for Kant is that there cannot be an infinite force that presses matter into an infinite small space. MFN, 4, 512. MFN, 4, 516. 34The fundamental role of Newtonian gravity becomes already clear in his first publication, the Thoughts on the True Estimation of Vital Forces . Kant thereby t ries to connect th e mathematical str ucture of the law of g ravitation (the rev erse squ are of the d istan ce) with t he dimens ion of space ( The under - lying mathematical argument —to put it into mathematical terms— ). Kant speculates that another arrangement of the mathe - matical str ucture b y God lead s to spaces with dif ferent di mension. Althoug h Kant does not explore these ideas in his latter works, the connection between the invers e square of grav ity and space can be fo und al so in t he dy Metaphysical Foundations of Natural Science . Kant thereby uses the three d i mensions of space that are given a priori to show that an attractive force must act proportional to the invers e square of the distance. -critical wri ting regarding Kant’s view on gr av ity as a matter constituting fundamental force is his dissertation Monadologia Physica . Newton’s methodology allows him to investigate the laws of na cannot explain the underlying reasons for their validity. This shows the need of a r econciliation of metaphysics and physics. Kant wishes explicitl y to develop a synthesis between Newton and his major rival in questions of natural philosophy: Leibniz. Kant modifies Leibniz’s idea that matter is constituted by monads. The m o nads of a b ody are finite and have a sphere of effectiv ity. Impenetrab i l ity is the co nsequents o f a repulsive fo rce by which other penetrating bodies are pushed back. Besides, there must be an attra c- tive force (otherwise the density of these bodies would endlessly decrease). Even thoug h Kant dismis ses a lot of these though ts in his crit ical period (cf. Kant , 2004: p. 41. MFN, 4, 505), the parallels to the (30 years later pub Metaphysical Foun dations of N at ural Scienc e are obvio us. Beside att raction , also rep ulsion can be fou nd in Newt on’s Principia , even though, as Kant realizes himself, not to the same extend (cf. Ca rrier, 1990: ; Kant, 1900a: p. 242. UTH, 1, 242). For a further analysis of the relation of Kant and Newton concerning the status of gravity cf. Fri edman 199 0. As Kant arg ues in t he gener al remar ks on dynamics, attract ion i s not grav - ity itsel f. Gravit y is the for ce by which bodies act on each other . The attrac - tion of bodies in contact is cohesion (Kant , 2004: p. 65. MFN , 4, 526). That means that Kant’s fundamental force is more basal and also includes other natural phenomena.  E. GÖRG Open Access physical Foundation of Natural Science39. This opinion goes hand in hand with Kant’s view on the metaphysical fundament of science, which he considers to be complete. There is no more to be done, or to be discovered, or to be added here, except, if need be, to improve it where it may lack in clarity or exactitude (Kant , 2007: p. 12)40. This opinion, as will be shown, is the essential difference between Kant and Fries. Fries’s Natural Philosophical and Mathematical Investigation in the Dynamics of the Mathematical Philosophy of Nature This part will first provide an overview of Fries’s revision of Kant’s natural philosophy in general. Then it will focus on Fries’s dynamics and his natural philosophical and mathemati- cal investigations. Its aim is to highlight how Fries extended Kant’s focus on mechanics. It will become clear that this pre- pared the ground for applying the fundamental forces on chem- istry, electricity and magnetism as discussed in the final chapter. Fries’s Relation towards Kant’s Philosophy The differences in Post-Kantian philosophy accrued from the answers that were given concerning the problems of critical philosophy41. The most important place of the reception of Kant’s works was Jena42. At this place, Fries listened to Fichte’s lectures and became an opponent of German ideal- ism43. One of the differences between Fries and the philoso- phers of German idealism is that he is not trying to build a new philosophical system, but “only” to revise Kantian philosophy. He therefore often tries to downplay the changes he made in his revision of Kant44. He saw himself as a pupil of Kant45, who simply accomplished the Kantian system46. For that reason, he is often (wrongly) labeled as a mere epigone of Kant47. Yet we find a lot of potential in Fries’s revision of Kant’s philosophy. Parts of Fries’s natural philosophy could provide the philoso- phy of science with new innovations, especially with regard to the interplay of mathematical and philosophical theory with empiricism. The Mathematical Philosophy of Nature as a Revis ed Extension of Kant’s Natural Philosophy As the title of Fries’s book indicates, he sets great value on the interplay between mathematics and natural philosophy. He thereby opposes the speculative natural philosophy of his con- temporaries Schelling and Hegel48. In the preface, Fries writes: If I’m not mistaken, Schelling’s philosopheme was re- moved from the application of the true mathematical me- thod due to its radical error and could therefore appeal it- self in its application to outer doctrine of nature only by the use of very undetermined general concepts (Fries, 1979: p. V). Fries said he chose the title Mathematical Philosophy of Na- ture instead of merely Natural Philosophy to underline the dif- ferences to Schelling’s approach and the importance of mathe- matics49 to support natural philosophy50. Fries’s Mathematical Philosophy of Nature must thereby be read as a revision of Kant’s natural philosophy. Two kinds of changes can be found: On the one hand, Fries’s aim is to accomplish the Kantian foundation of Newtonian science. That means that he tries to overcome Kant’s shortcomings51. For example: Kant used fun- damental concepts of Newton’s system, such as absolute space, and reinterpreted them in a completely new way. Absolute space became thereby a “mere idea” (Kant, 2004: p. 98)52 closely connected to the first cosmological idea of the Critique of Pure Reason. In his Mathematical Philosophy of Nature Fries tries to develop a theory of movement that does not re- quire such an idea and is based wholly on relative space53. On the other hand, Fries tries to expand the application area of the Metaphysical Foundation. While Kant, in his publica- tions, considered his Metaphysical Foundations of Natural Science as completed, Fries tries to incorporate the latest scien- tific developments54. The following examination of this ap- proach will concentrate on the dynamics and the conception of It would therefore be impossible to introduce, for instance, some thing like Coulomb’s law as a fundamental force (for an opposite opinion cf. for i , 1994: p. 328, and the critique of this position by Carrier, 1990 MFN, 4, 476. cf. Bonsiepen, 1997: p. 14. cf. Wundt, 1932: p. 140. Although I do not share Kuno Fischer’s general valuation of Fries’s ph ified in emphasizing this particular antagonism (cf. Fis , 1862). Fischer’s speech has rightly been called a “funeral eulogy” on Fries’ s philosophy (cf. Wundt, 1932: p. 381, for an analysis of Fischer’s argumentation cf. Geldsetzer , 1999: 26-30). Fisc her tries to show that the true heirs of Kant’s philosophy are Reinhold, Fichte, Schelling and Hegel, while Fries supposedly misunderstood the true nature of the a priori by introducing anthropology into Kant’s philosophy (concerning a more veri- dical ana lysis of Fries’s i dea of anthropol ogy and its relat ion to critical phi , 1906: pp. 1- 14, for a refutation of the accusation of psychologism cf. Sachs -Hombach, 1999). There are other reasons for the underestimation of Fries’s philosophy: For one, Fries was banned from uni - versity for political reasons (e.g. his participation at the Wartburg Fest i val and the murder of August von Kotzebue by his pupil Ludwig Sand). Second, Fries wr ote in a time when natural scien ce emancipated i tself fro m philoso - phy and b ecame the major r ational aut hority (cf. Pu lte , 2005: p. 101). F ries, however, tried to hig hlight th e necessity o f an inter play between p hilosop hy and science. This was very much against the philosophical mainstream of this time (Pulte , 1999: pp. 63-67). Two Friesian schools developed out of Fries’s philosop hy. The main fig ure of the first was Ernst Friedrich Apelt, of the second Leonard Nelson. The reception of Fries’s philosophy has increased in the last decades, probably due to the pub lication of t he complete edition of Fries’s works. cf. Pulte, 1999: p. 60. The only biography of Fries was written by his son-in- law Ernst Ludwig Theodor Henke (Henke , 1937). A biography which examines Fries in a broader historica l context is still a desideratum. cf. Arjomand, 1987: p. 93. 47For a more thorough analysis of the reasons for the comparatively poor reception of Fries see Pulte , 1999. For an analysis of the antagonism between Fries and the speculative ph i- losophy of nature see Bonsiepen, 1997. The first part of Fries’s Mathem at i cal Philo sophy of Nature (more than the first half of the volume) tries to develop a philosophy of mathematics i n - spired by Kant. This is later applied to natural philosophy in the “ ”, which is investigat ed here. Fo r an analysi s of Fries’ ophy of mathematics cf. Schubring, 1999. cf. Fries, 1967: pp. III-VI and for example Arjomand, 1987: pp. 95-96. “Pure kinetics as an independent theory was first developed by Newton, but recei ved a comp letely n ew clari ficatio n by Kant’ s metaph ysical f ound a - tions of natural science. Now it depends on a happy unification of the ma- thematics of Newton and the philosophy of Kant.” (Fries, 1979: pp. 397 2MFN , 4, 559. F or a discussion of Kant’s transfo rmation of absolu te space cf. Friedman , 1992: pp. 136-164. cf. Fries, 1979: pp. 422-425 and Görg, 2013. This becomes clear by the full title Mathematical Philosophy of Nature , arranged by philosophical method, an approach.  E. GÖRG Open Access fundamental forces by which Fries tries to derive an a priori basis of possible matter-constituting forces. These a priori shapes of possible forces guide scientific research as heuristic maxims. Fries’s Dynamics As shown, Kant excluded chemistry from proper science. He dealt mainly with mechanics. Electricity and magnetism are hardly dwelt upon. In fact, Coulomb published his fundamental findings on the force between two charged bodies in the year 1784. In the late 18th century, Lavoisier developed the funda- mental methods and concepts of chemistry. So the Metaphysi- cal Foundations of Natural Science where written at a time when several “experimental doctrines” (Kant, 2004: p. 7)55—as Kant would have called them—were still developing, while Kant wrote a priorical cementation of the “old” natural science, and thought this foundation to be complete. The Preface to Kant’s Metaphysical Foundations of Natural Science is there- fore a paradigmatic text for the classical conception of natural science. In contrast, Fries’s Mathematical Philosophy of Nature can be read as a first careful attempt to provide modernized science with a philosophical foundation56. Kant, polemically spoken, viewed large parts of natural science, as an appendix of philosophy, while on the contrary Fries views science as some- thing more autonomous. This view goes hand in hand with the development and emancipation of natural science in this time57. For that reason, Fries enlarges the dynamics and introduces additional, merely possible, forces. Kant’s “remarks” on dy- namics are therefore expanded in a new chapter, under the name “stoechiology”. Fries here tries to integrate chemistry into natural science by an advanced application of dynamics onto the constitution of matter. Right at the beginning of the dynamics, Fries sketches his program. He writes: Substance and force are representations of philosophical origin and are here linked a priori to mathematical repre- sentations of movement. So the direct method of this in- vestigation is given to us in such a way that we combine the basic concepts in metaphysical respect with mathe- matical constructions. Either we know nothing about these things or in form of such a philosopheme (Fries, 1979: p. 443). It is clear that this is Kant’s handwriting, even though there are differences between Kant’s approach and Fri es’ s revision. As shown before, Kant underlines the importance of a mathe- matization, through which an experimental doctrine can gain the status of properly so called natural science. Beside the me- taphysical construction58 Kant tries to demonstrate the “prin- ciples of the construction of these concepts (and thus principles of the possibility of a mathematical doctrine of nature itself) […]” (Kant, 2004: p. 9)59. This possibility of mathematization is enabled by the construction of movement in the phoron- omy60. However, Kant never exceeds the principles of mathe- matical construction. In his Metaphysical Foundations of Na- tural Science he nearly always avoids the use of mathematics. Fries in contrast uses mathematics as a criterion for the evalua- tion of possible fundamental forces. So Fries combines phi- losophical investigations of nature with mathematical construc- tion. Fries’s Natural Philosophical Investigation of Possible Forces Matter is investigated concerning its movement, whereby every change, that means an acceleration61, has a cause that arises from the interaction of bodies due to their fundamental forces. The simplest proportion between two points in space is a straight line. The length of this straight line can be increased or diminished. Fries concludes: Accordingly, every fundamental force is a cause of altera- tion of this straight line between two points. Therefore, there are two basic forms of fundamental forces, for they either diminish the distance between two points, and are thus attracting forces, or extend it, and hence are repulsive forces (Fries, 1979: p. 451). So far Fries follows Kant. But since these attracting and re- pelling forces can be surface forces or forces that act at a dis- tance, Fries extends Kant’s types of fundamental forces from two to four62. Besides attraction at a distance, repulsion at a distance is possible as well. And apart from repulsion as a sur- face force, Fries introduces attraction as another surface force. Fries uses attraction to provide an understanding of chemical reaction, while repulsion at a distance helps him to integrate electrical interaction. The degree to which two masses act on each can only be de- rived empirically. It was said before that Fries considers phi- losophy, mathematics and experience as necessary components of natural science. Thereby, in contrast to Kant, Fries gives more space to experience and mathematics, while the possibili- ties of philosophy are diminished. The equality between heavy and inert mass has to be derived empirically and is not under- standable a priori. It is indeed a matter of experience that all heavy sub- stances of our solar system show the same degree of gra- vitation. Nothing whatsoever induces us to apply this sen- tence to the spatial universe. Who compares more precisely will surely find it impossi- ble to establish the height of fall of 15 feet for the surface of the earth philosophically and to anticipate experience; what should appear, though, if the specified degree of force, assigned to a specific kind of mass, would be the MFN, 4, 470-471. 56Concerning the differences between classical and modern science cf. e.g. Die mer , 1968. In Fries’s concep tio n of nat ur al s cien ce and it s s uppo rt b y na - tural philosophy some tendencies of the criteria of modern sc ience by D mer can be found. As Herrmann underlines, Fries’s conception cannot be seen as the starting point of a modern understanding of natural science b e- cause of i ts limited in fluence (cf. Her rmann , 2012: pp. 54-55). Further more, there are still a lot of very classical elements in Fries’s system (like for instance his strict denial of atomism because of a priori metaphysical co n - siderat ions). Neverth eless, it sh ows that Fries was aware of th e changes th at where going on in the conceptions of science , p hilosophy and their inte rplay. For an analysis cf. Jungnickel & Mc Cormmach, 1986: pp. 34-62. 58cf. Kant, 2004: p. 9. MFN, 4, 473. MFN, 4, 473. “Phoronomy is thus the pure theory of quantity (mathesis) of mo , 2004: p. 25. MFN, 4, 489). “I underst and force only as t his term accordin g to which matter is thought of as a caus e of th e in creas e or decr ease o f mo tion acco rding to a cer tai n l aw of interplay between other masses.” (Fries , 1979: p. 451). 62The “line forces” shall be discussed later. 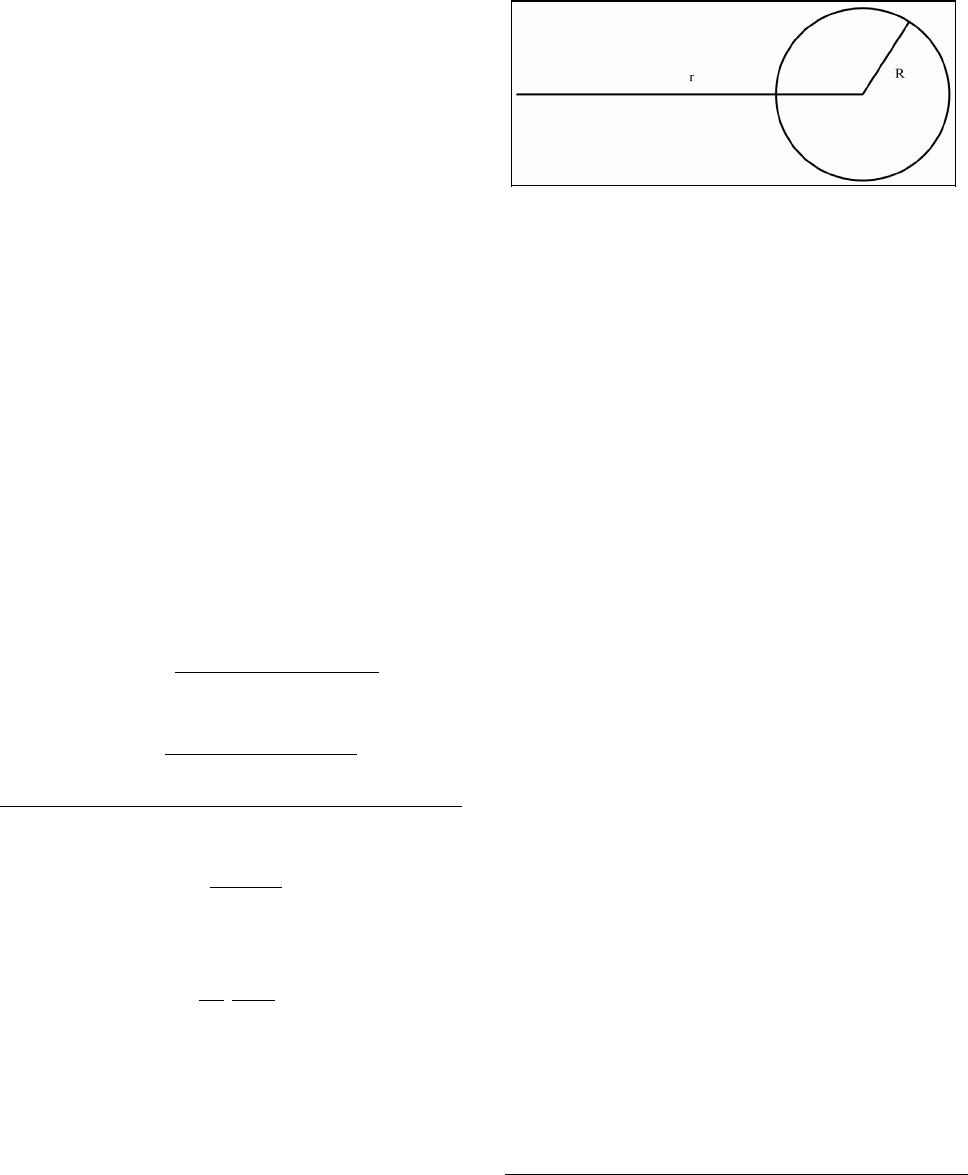 E. GÖRG Open Access same for all matter (Fries, 1979: p. 453)63. This establishes the possibility of applying other forces that do not act proportionally to the masses they are accelerating. Fries’s Mathematical Investigation of Possible Forces Forces have to fulfill certain mathematical conditions. For example, a force that is acting at a distance has to be continuous in every place. From this, Fries generates a mathematical inves- tigation of possible fundamental forces. He characterises the difference between him and Kant as follows: Kant did not consider that the construction a priori here rather belongs to pure mathematics and must be judged according to its laws. So his metaphysics arrogates too much by assigning every possible matter these two forces a priori and even specifies the degree of attraction. On the other side, it undertakes too less by misjudging the mathe- matical nature of this investigation (Fries, 1979: pp. 460- 461). In this mathematical investigation, Fries analyses the effect of a globe of matter on an arbitrary chosen point in space. The force of the globe of matter has to conform to the above-men- tioned conditions. A mass point would act upon another with the following force64: (5) Whereby r is the distance between the two mass points and c is a constant. Fries now applies this law to a globe of matter65 with the radius R (Figure 1): ( )() ( ) ( ) ()( ) 3p 3p 2 2πRrR rR F p,rc1p 3pr −− + +− =⋅ −⋅−⋅ () () ( ) () () () 5p 5p 22 2πrR rR c1p3p5pr −− + −− −⋅ −⋅−⋅−⋅ (6) Figure 1. A globe with the r adius R that acts on a point with the distance r to the center. Fries’s aim is to investigate the different mathematical prop- erties of the globe of material globe for different exponent’s with a integer p. Fries’s Concrete Application of His Dynamical Theory on Chemical Dissolution, Coulomb’s Law and Magnetism According to Fries, a dynamical theory of matter has several advantages over atomism. One of them is that it liberates phys- ics from the mere hypothesis of absolute hard bodies. Further- more, it allows a deeper understanding of physical phaenomena. Fries uses Newton’s theory of gravity to illustrate this. Without the dynamical theory of matter, the law of gravitation would be in danger of being an “arbitrary hypothesis” (cf. Fries, 1807: p. 213). He elaborates on the benefits of a dynamical theory as follows: Dynamics sides the mechanic impenetrableness of matter through compression with a chemical one, according to which matter can continuously combine itself with other matter, be heated or be run through light. Thus, we bring nearer the teaching of the forms of aggregation, of spe- cific adhesion, of magnetism, electricity and all atmos- pheric processes, of chemical mixtures and decomposi- tions and, eventually, also of the evaporation and the for- mation of crystals to mathematical theory (Fries, 1975: pp. 235-236). The following part will analyze how this advance towards a mathematical theory takes place in chemistry, electrostatics and magnetism. Chemical Interaction through Attracting Surface Forces With his “General Remarks to Dynamics” that conclude the second chapter of his Metaphysical Foundations of Natural Science, Kant engages in concrete discussions of his time66. His main aim is to continue his critique of a mathematical engage- ment of space, i.e. atomism as represented by his contemporary Lambert. In the light of critical philosophy, the reason for Kant’s attack is the second Antinomy of the Critique of Pure Reason67. In the dynamics he concludes: cf. as well Fries’ letter to Apelt from the 7.7. 1834 in Fries, 1997: p. 68. This can be illustrated by a look onto the law of gravitation. The force that acts upon a body is: (1) Whereby th e indices 1 and 2 ar e labelin g the bodies , while th e indices i and g are label i n g in ert and gravi t at i on al m as s . a stands f or acceleratio n an d r for the dist ance between these bodies. Γ is in case of the law of gravitation the The acceleration up on this body is given by: (2) For Kant, the force by which bodies act upon each other is gra vi ty. The equival en ce of inert and gr av i t at io nal mass can th us b e derived a pr io ri . T h at means that only the gravitational constant must be dete r mined empirically. For Fries, in contrast, this equivalence can only be derived by experiment (cf. Herrmann , 2000: p.164-165). The idea be hind this may be that it enables us to integrate the action of charged bodies as well. The author uses a different notation than Fries does in his Mathe matical Philosophy of Nature . Thereby F is the force, r the distance between the investigated point and space and the middle of the globe, R the radius of the globe and p the exponent. For the law of gravita t i on this would mean: For the sak e of brev it y, I s kip the concr ete mathe mati cal der i vation here. It can be found in Fries , 1979: pp. 461-464. I will thereby consider only the problem of the dissolution of matter. For a broad analysis of Kant’s contribution to chemistry compare Carrier 1990. cf. Kant, 1929: pp. 405-408. CpR, 438-443/466- 471. In the proof of the Antithesis Kant writes: “An absolutely simple object can never be given in any possible experiences. And since by the world of s ens e w e must mean the sum of all possible experiences, it follows that nothing simple is to be found anywhere in it.” (Kant, 1929: p. 404. CpR, 437/465).  E. GÖRG Open Access Matter is divisible to infinity, and, in fact, into parts such that each is matter in turn. (Kant, 2004: p. 40)68. Kant declares that absolute impenetrability is a “qualitas oc- culta.”69 But he also has to admit that the “mathematical-me- chanical mode” has its benefits with regard to his dynamical matter-conce ption 70. It explains the differences between diverse kinds of matter (cooper, iron etc.). One of the main aims of the “General Remarks to Dynamics” is therefore to counteract the shortcomings of dynamics in regard to atomism. This opposition is shared by Fries. In the year 1807, Fries released a piece of writing with the meaningful title Atomism and Dynamics71. Fries’s statement about the two distinct meth- ods of natural science and the rank he ascribes his refutation of atomism are particularly interesting. On the one hand, there is the constitutive method. It leads, as Fries says, to a system of mathematical physics like it was given by Newton or Laplace72. On the other hand, rational inductions are made by means of heuristic maxims. The question whether or not matter is con- structed out of atoms or dynamically is settled by the constitu- tive method. In Fries opinion, and here he follows Kant, it can be shown beyond all doubts that indivisible matter does not exist and that chemistry based on atomism relies on an empty concept. The question of how chemical reaction takes place is yet unanswered by constitutive theory. Fries’s a im is to use the fundamental forces as guiding heuristic maxims to incorporate chemistry into mathematical physics. This approach will be analyzed in the following. Right in the first paragraph of the dynamics he declares that the question whether matter is constituted by atoms cannot be answered by experience but only by an a priori investigation73. That Fries, in difference to Kant, raises this question right at the beginning of the chapter can be seen as an increase of pressure from empirical science and atomism. The reason why Fries as well as Kant stick to a dynamic theory of matter is that absolute hard bodies presume an infinite resisting force in case of colli- sion. This mathematical argument is supported by metaphysical arguments. Empty space in which atoms move can never be part of experience because we experience space just because of the matter that fulfills it. Space is the mere form of our outer experience74. Furthermore, metaphysics shows that the never ending divisibility of space goes hand in hand with the divisi- bility of matter. In his aim to extend Kant’s Metaphysical Foundation of Natural Science, Fries’s includes two additional chapters: “Stoechiology” and “morphology”. The first applies the before derived possible forces to the structure of matter and its interac- tion. This must be read as an extension of Kant’s “General Re- marks to Dynamics”, for Fries deals with aspects of natural science which have not been dealt by Kant. Substances are differing from each other not because they are build out of different assembles of one underlying substance. This would be the kind of atomism Newton has in mind: According to the atomistic opinion, all matter should be made of one kind of substance and just differ by the me- chanical proportion of composition. Even Newt on consid- ers this (Cor. 2. Prop. 6. Lib. 3. Princip. Phil. Nat.) to be evident (Fries, 1979: p. 541)75. The different kinds of matter can therefore be distinct only because of the combination of inherent forces76. Fries draws on a larger pool of inherent forces to explain these differences. Like Kant, he distinguishes between mechanical and chemical interaction. If two masses interact mechanically, they interact by impact. Thereby, the bodies cannot invade each other be- cause of the force of repulsion. In the collision of two bodies, the volume of the bodies can be diminished but never become zero. So fare Fries does follow Kant77. Kant thought of chemical interaction in the following way: This chemical influence is called dissolution, insofar as it has the separation of the parts of a matter as its effect. (Kant, 2004: p. 69)78. As Kant realizes, this separation of parts leads to several problems. If dissolution is thought of as the separation of parts of two substances till they both engage one and the same space, it includes a “completed division to infinity” (Kant, 2004: p. 70)79. Completed division to infinity was what Kant opposed in his antinomies. Kant tries to “rescue” the ar- gument by saying that the dissolution happens in finite time because the separation accelerates if the parts of matter become smaller. That means that the sequence of partings is infinite but the time in which this partings take place is finite. Nevertheless, dissolution stays something “inconceivable”: The inconceivability of such a chemical penetration of two matters is to be attributed to the inconceivability of dividing any such continuum in general to infinity (Kant, 2004: p. 70)80. Fries believes that Kant is hoodwinked by atomism. Chemi- cal interaction should not be explained by the division, but rather by the invasion of bodies into each other by the action of attractive surface forces81. If masses dissolute by chemical in- MFN, 4, 503. Kant, 2004: p. 46. MFN, 4, 502. “And here the mathematical-mechanical mode of explanation has an ad - vantage over the metaphysical - dynamical [mode], which cannot be wrested from it, namely, that of generating from a thoroughly homog e neous materi al a great sp ecific var iety of matters , which vary bo th in d ensity and (if for eign forces ar e added) mod e of action , through th e varying shape o f the part s and the empty interstices inte rspersed among them.” (Kant, 2004: p. 63. MFN -525). He thereby opposes not only atomism but also Schelling’s complete redu forces. Fries, 1975: pp. 223-224. “On calls extension and impenetrability primary general proper ties of matter and often claims th at experience t eaches that all matter is impenet r a - ble and even that there are empty gaps between its impen etrable parts. But the debate on how we should conceptualize this impenetrabi l ity and the differen t kinds of density i s a philo soph ical- mathematical one and cannot be solved by experience.” (Fries, 1979: p. 444). 75Whereas Kant does not reject Newton’s atomism, Fries does explicitly criticize Newton . “[…] [O]ne can only take two paths in this connection: the mechanical the absolutely full with the absolutely empty, and an oppos dynamical path, by mere variety in combining the original forces of repulsi on an d attraction to explain al l differ ences of matter s (Kant, 2004: -72. MFN, 4, 532. cf. Fries, 1979: pp. 540-541). Kant, 2004: p. 69. MFN, 4, 530. MFN, 4, 530. MFN, 4, 531. MFN, 4, 531. “The dissolution results in the mixture of matter, which we ought to di s- tinguish from the mechanical mix of unequal parts. As for the mixture, we cannot assume that th e different parts of matter are arranged in small co m- pounds of equal size. Rather, we assume that they jointly engage the same space. According to atomistic physics, such would not even occur .” (Fries  E. GÖRG Open Access teraction, they invade each other (which is impossible from Kant’s point of view). This is possible because they are pulled into each other due to the attracting surface force82. This attrac- tion as surface force thereby solves the problem of chemical interaction in Kant’s philosophy: Although Kant realized the possibility of such dissolution, was guided by the atomistic prejudice to construct the dissolution as mixture that could be become ever more subtle; he doubt that real dissolution appears in nature and holds it to be indecomposable (Fries, 1979: pp. 551-552). Given the increasing success of atomism in the nineteenth century, Fries extension of Kant’s dynamical theory can, some- how, be seen as a dead end. Fries himself considered his ap- proach to integrate chemistry into dynamics as mistaken: Regardless of the warnings Kant issues in the preface to his Metaphysical Foundations of Natural Philosophy, I always entertained the hope of developing the mathemat- ical-philosophical teachings of his dynamics further to eventually apply it on chemical forces as well. I struggled a lot and for a long time, but with little success (Henke, 1937: p. 49)83. But still, Fries’s theory of dissolution closes a gap in Kant’s dynamical theory of matter. Electricity as Repulsive Action at a Distance and Magnetism as “Line Force” To understand the form of the electrostatic interaction, it is necessary to understand the mathematical form of the force in question. Fries talks about this in his “Mathematical investiga- tions of the dynamics”. In this case p = +2 like in the case of the law of gravitation or Coulomb’s law. This leads to: ( )() () ( ) () () 32 32 2 2πRrR rR F 2,rc12 32r −− + +− =⋅ −⋅−⋅ ()( ) () ()() () 5252 22 2πRrR rR c1232 52r −− + −− −⋅ −⋅−⋅−⋅ (7) (8) Fries then introduces two fundamentally different kinds of matter that differ from each other because of the inherent forces that act at a distance: Therefore, two kinds of matter or substances have to be distinguished, heavy, weighable (ponderable) sub stances and luminous f luids, light substances (Fries, 1979: p. 546). Heavy substance is characterized by the fact that both, attrac- tion as action at a distance (inversely proportional to the square) and repulsion as surface-force, are inherent to it. That means that they are acting in accordance to the law of gravitation, an d the law of Mariotte. As mentioned before, the force of gravita- tion is not necessarily proportional to the inert mass of the bod- ies (Fries even ponders the possibility of a negative attraction of heavy matters onto each other). The force of electrostatics differs from gravity not because of its mathematical form but because of its substance. While grav- ity acts between heavy matters, Fries introduces another type of substance, “luminous fluids”. He explains: Eventually, a mass is called luminously fluid if its move- ment is mainly determined by inherent, pervading forces of repulsion (Fries, 1979: p. 546). Fries differentiates between two types of “electricity”, i.e. two types of luminous fluids84. Towards a fluid of the same kind it acts with a repulsive force proportional to the square of the distance. The different kinds of the luminous fluid attract each other proportional to the square of the distance. The elec- trical fluids act upon each other only at a distance, not by con- tactforces. If the fluids are mixed85 in equal parts, the forces of repulsion and attraction compensate each other. Fries calls this connection the fluid indifferent electricity86. This, however, must be rated as a far-reaching mistake by Fries, for he underestimated the experiment of Oersted87. Fries’s aim was to build a connection between the theories of heat, light and electricity while Oersted linked electricity and magnetism88. Concerning the scientific status of magnetism compared with electricity Fries w rites: It is true that all our theoretical views on the nature of electricity remain insufficient. This, however, applies all the more to our accounts of magnetism (Fries, 1974: p. 113). Fries wants to remove this derivative by “line forces”. His theoretical account of magnetism is thereby much more com- plex and complicated. He concedes that most of his account is hypothetical at best. Considering natural philosophy it can be claimed that action at a distance is antiproportional to the square of the distance (~1/r2) and that a surface force acts anti- proportional to the volume (~1/r3) occupied by a body. Analo- gously, one can assume another kind of force, “Linienkräfte”, that act antiproportionally to the distance (~1/r). Fri es writes: The natural-philosophical analogy obviously leads to this precondition and will demand that they be effective ac- cording to the law of their diffusion with inverse propor- tion to the distance (Fries, 1979: p. 459). According to this theory, Fries tries to supply magnetism 82“An applicat ion of mathematics o n parts of chemist ry is thereby what can give chemistry the status of a proper science. This is made possible by the attractiv e surface fo rces that fo rm the bas ic relation of chemic al substan ces. Apart from external pressure, attracting, and maybe also repelling, surface forces ar e fun dament al fo r all c hemical i nter action s of m atter. ” (Fr ies, 1974 For a further evaluation of Fries’s intensive approach on chemistry cf. König & Geldsetzer, 1975: pp. VII-XXV. 84 Fries thus supports Symmer’s hypothesis of two fluids and argues against Franklin’s assumption of just one fluid. He points out explains the repulsive force between two negative charged conductors Fries, 1826: pp. 472-473; Herrmann , 2000: pp. 179-180). 85 These mixed electrical fluids act on each other only at distance. Hence, the decomposition of these fl uids would be easy if they touch a surface that acts with different surface forces on the electrical fluids. Furthermore, Fries tries to explain the difference between a conduct ing and a non-conducting me their repulsion at contact with these electrical fluids. 86The indifferent electricity is a “heat substance” (“Wärmestoff”, cf. Fries 1979: p. 560) . 87cf. Herrmann, 2000: p. 187. 88 While it seemingly s upports Schel l ing’s dynamical theory. 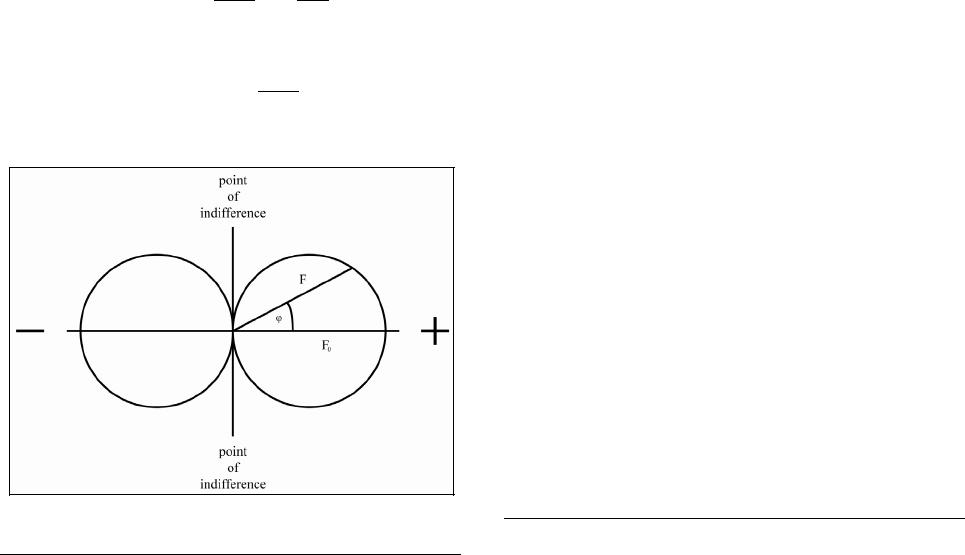 E. GÖRG Open Access with an underlying heuristic maxim that supports rational in- duction. At the end of the dynamics, Fries continues with his investigation of “line forces” in a mathematical way. Important is that it is not his aim to show how the phenomena of magnet- ism functions, but to facilitate experimental investigation: Finally, I must add a remark on the above-mentioned line forces, about which I do not know whether they could re- veal useable consequences. Apart from those fundamental forces which act with inverse proportion to the square of the distance, mathematical theory shows us that also forces which act in the inverse proportion of the distance are possible. According to natural philosophy, this is the proportion of extension in a straight line; hence, we must presume a force that acts just in one direction, which could be called line force (Fries, 1979: p. 493). The ensuing mathematical discussion shall, in parts, be re- constructed here. First of all, Fries introduces the “line force” as a force that acts proportional to the reciprocal distance. It thereby attracts in one direction and repels to into the other. Fries designates these poles with + and −. If the force is acting beside the poles, just a part of the force is affecting. (9) This can be illustrated as follows (Figure 2): As he did with regard to the other forces, Fries also investi- gates this type of force mathematically. In contrast to these other forces, the line forces are functions of an angle89. If a body would possess such line forces, and a row of them would be polarized other rows would accrue with the same direction. If the line forces of, say, a globe were all adjusted to the same direction, they would, as Fries shows, act according to the force: ( ) 32 32 4πR 2R F1, rc1 r 5r =⋅ ⋅− (10) The action of the globe at its surface (r = R) would lead to: (11) If the radius of the globe would be increased, the force would Figure 2. The action of a line force. increase as well. This means that line forces act at a distance, not by contact. From this theoretical explanation, Fries con- cludes several properties of lodestone: A mass which posses these forces in its parts would allow different states of polarization and depolarization. It would be polarized if the axes of its smallest parts were organized in one direction and depolarized if these axes were scattered without arrangement in all directions. In a depolarized state, the whole mass would show no line force because the action of the different parts would eli- minate each other, whereas in a polarize d state, the whole mass would have attracting and repelling poles like a magnet and between that a point of indifference. But since these forces disappear in contact, a depolarized mass would not polarize itself. Rather, its polarization would need outer inducement, e.g. through the attraction and repulsion of another, already polarized mass. It would behave like the magnetized iron, at the sweep of the mag- net. It could be depolarized again through intense inner concussions or irregular movements of its small parts (Fries, 1979: p. 497). Fries concludes further that line forces could explain pro- perties of the crystallisation of matter90: In doing so, he fills the gap in Kantian philosophy on how to explain the different types of matter: The greatest variety of specific diversities among sub- stances may be constructible by the line forces, by which we find reasons of explanation for specific configuration, in case hypotheses of this kind are valid at all (Fries, 1979: p. 547). Conclusion Kant’s Metaphysical Foundations of Natural Science is closely linked to the dominant research field of physics of his time, mechanics. An application of his natural philosophy on many scientific achievements that accrued after Kant is there- fore difficult. Fries relates Kant’s natural philosophy to the latest scientific developments and tries to support them by his investigations. His Mathematical Philosophy of Nature can therefore be understood as a linkage between Kant’s natural philosophy and the changing in the conception of natural sci- ences. The inclusion of a revised chemical interaction, electro- statics and magnetism by an extended and more elaborated dynamics shows how he tried to concretely apply his natural philosophy to the natural sciences of his time. Even if these theoretical explanations are outmoded today, they can give stimuli on how a revised extension of Kant’s natural philosophy could be possible. Further investigations could therefore try to build a link between Fries’s revision of the Kantian approach and the actual debate about a relativised a priori91. REFERENCES Arjomand, K. A. (1987). Entdeckung und Rechtfertigung in der Wissenschaftsphilosophie des 19. Jahrhunderts. Unter besonderer Berücksichtigung der Entwicklung in Deutschland ca. 1800-1875. Frankfurt am Main: Peter Lang. For that reason Fries has to modify Equation (6). Cf. Fries 1979, pp. 498-499. I thank Helmut Pulte, Janelle Pötzsch, Tobias Schöttler and Anna- Lena Thiel for their helpful comme nts and advices concerning this paper.  E. GÖRG Open Access Bonsiepen, W. (1997). Die Begründung einer Naturphilosophie bei Kant, Schelling, Fries und Hegel. Frankfurt am Main: Vittorio Klostermann. http://dx.doi.org/10.3196/9783465028895 Carrier, M. (19 9 0 ). Kants Theorie der Materie und ihre Wirkung auf d ie Zeitgenössische Chemie. Kant-Studien, 81, 170-210. http://dx.doi.org/10.1515/kant.1990.81.2.170 Clarke, S. (1717). A Collection of Papers, which passed between the late Learned Mr. Leibniz, and Dr. Clarke, In the Years 1715 and 1716. London: James Knapton. Diemer, A. (1968). Die Begründung des Wissenschaftscharakters der Wissenschaft im 19. Jahrhundert—die Wissenschaftstheorie zwis- chen klassischer und moderner Wissenschaftskonzeption. In A. Die- mer (Ed.), Beiträge zur Entw icklung der Wissenschaftstheo rie im 19. Jahrhundert (pp. 3-62). Meisenheim am Glan: Verlag Anton Hain. Elsenans, T. (1906). Fries und Kant. Ein Beitrag zur Geschichte und zur systematischen Grundlegung der Erkenntnistheorie. I. Histo- rischer Teil. Jakob Friedrich Fries als Erkenntniskritiker und sein Verhältnis zu Kant. Gießen: Töpelmann. Euler, L. (17 36). Mechanica sive motus scientia an alytice exposita. Pe- tersburg: Typographia Academiae Scientiarum. Euler, L. (176 5). Theoria motus corporum solidorum seu rigidorum ex primis nostrae cognitionis principiis stabilita et ad omnes qui in huiusmodi corpora cadere possunt accommodata. Rostock: Röse. Euler, L. (1802). Letters of Euler on Different Subjects in Physics and Philosophy. Addressed to a German Princess. London: Murray and Highley. Fischer, K. (1862). Die beiden kantischen Schulen in Jena. In Aka- demische Reden (pp. 79-102). Stuttgart: Cotta’scher Verlag. Friedman, M. (1990). Kant and Newton: Why Gravity is Essential to Matter. In P. Bricker, & R. I. G. Hug hes (Eds.), Philosophical Pers- pectives on Newtonian Science (pp. 203-209). Cambridge, Mass.: MIT Press. Friedman, M. (1992). Kant and the Exact Sciences. Cambridge: Har- vard University Press. Fries, J. F. (1967). Neue oder Anthropologische Kritik der reinen Ver- nunft. In G. König, & L. Geldsetzer (Eds.), Jakob Friedrich Fries Sämtliche Schriften (pp. 4-6). Aalen: Scientia Verlag. Fries, J. F. (1971a). Grundriß der Logik. In G. König, & L. Geldsetzer (Eds.), Jakob Friedrich Fries Sämtliche Schriften (pp. 29-152). Aalen: Scientia Verlag. Fries, J. F. (1971b). System der Logik. In G. König, & L. Geldsetzer (Eds.), Jakob Friedrich Fries Sämtliche Schriften (pp. 153-632). Aalen: Scientia Verlag. Fries, J. F . (1974). Entwurf des Systems der theoretisch en Physik. In G. König, & L. Geldsetzer (Eds.), Jakob Friedrich Fries Sämtliche Schriften (pp. 257-400). Aalen: Scientia Verlag. Fries, J. F. (1975). Atomistik und Dynamik. In G. König, & L. Geldsetzer (Eds.), Jakob Friedrich Fries Sämtliche Schriften (pp. 223-257). Aalen: Scientia Verlag. Fries, J. F. (1979). Die Mathematische Naturphilosophie nach philo- sophischer Methode bearbeitet. Ein Versuch. In G. König, & L. Geldsetzer (Eds.), Jakob Fried rich Fries Sämtliche Schriften. Aalen: Scientia Verlag. Fries, J. F. (1997). Briefe I, [Konvolute A-E]. In G. König, & L. Geldsetzer (Eds.), Jakob Fried rich Fries Sämtliche Schriften. Aalen: Scientia Verlag. Fries, J. F. (2011). Briefe III, [Konvolute W,Z; Einzelbriefe; mit mit zwei faksimilierten Autographen]. In G. König, & L. Geldsetzer (Eds.), Jakob Friedrich Fries Sämtliche Schriften. Aalen: Scientia Verlag. Geldsetzer, L. (1999). Jakob Friedrich Fries’ Stellung in der Philo- sophiegeschichte. In W. Hogrebe, & K. Herrmann (Eds.), Jakob Friedrich Fries, Philosoph, Naturwissenschaftler und Mathematiker (pp.13-56). Frankfurt am Main: Peter Lang. Gloy, K. (1976). Die kantische Theorie der Naturwissenschaft. Eine Strukturanalyse ihrer Möglichkeit, ihres Umfangs und ihrer Grenzen. Berlin: De Gruyter. Görg, E. (2014). Kant und Fries: Krit ik des newton schen Rau mes. In S. Bacin, A. Ferrarin, C. La Rocca, & M. Ruff ing (Eds.), Kant und die Philosophie in Weltbürgerlicher Absicht. Akten des XI. Kant-Kon- gresses 2010 (vol. 5, pp. 55-64). Berlin: De Gruyter. Heidegger, M. (1962). Die Frage nach dem Ding. Zu Kants Lehre von den transzendentalen Grundsätzen. Tübingen: Niemeyer. Henke, E. L. T. (1 937). Jacob Friedrich Fries. Aus seinem han dschrift- lichen Nachlaß dargestellt. Berlin: Verlag “Öffentliches Leben”. Herrmann, K. (2000). Mathematische Naturphilosophie in der Grund- lagendiskussion. Jakob Friedrich Fries und die Wissenschaften. Göt- tingen: Vandenhoeck & Ruprecht. Herrmann, K. (20 12). Apriori im Wandel. Für und w ider eine kritische Metaphysik der Natur. Heidelberg: Universitätsverlag Winter. Jungnickel, C., & McCormmach , R. (1986). Intellectua l Matery of Na- ture. Theoretical Phys ics from Ohm to Einstein . Vol. 1. The Torch of Mat hematic s 1800-1870. C hicag o: The Unive rsit y of Chi cago Press. Kant, I. (1900a). Allgemeine Naturgeschichte und Theorie des Him- mels. In Gesammelte Schriften (pp. 215-368). Berlin: De Gruyter. Kant, I. (1900b). Metaphysicae cum geometria iunctae usus in phi- losophia naturali, cuius specimen I. continet monadologiam physi- cam. In Gesammelte Schriften (pp. 473-487). Berlin: De Gruyter. Kant, I. (1905). Neuer Lehrbegriff der Bewegung und der Ruhe. In Gesammelte Schriften (pp. 13-25). Berlin: De Gruyt er. Kant, I. (1922). Briefe 1747-1788. In Gesammelte Schriften. De Gruy- ter: Berlin. Kant, I. (1929). Critique of Pure Reason. Translated by N. K. Smith. London: Redwood Press Limited. Kant, I. (1938). Opus postumum. In Gesammelte Schriften. Berlin: De Gruyter. Kant, I. (1 968). Ne uer Lehrbegriff der Bewegung und der Ruhe. In Ge- sammelte Schriften (pp. 13-25). Berlin: De Gruyter. Kant, I. (1997). Metaphysische Anfangsgründe der Naturwissenschaft. With an introduction published by K. Pollok. Hamburg: Meiner. Kant, I. (2004). Metaphysical Foundations of Natural Science. Trans- lated by M. Friedman. Cambridge: Cambridge University Press. http://dx.doi.org/10.1017/CBO9780511809613 König, G., & Geldsetzer, L. (1975). Vorbemerkung der Herausgeber. In G. König, & L. Geldsetzer (Eds.), Jakob Friedrich Fries Sämtliche Schriften (pp. VII-XLI). Aalen: Scientia Verlag. Newton, I. (1726). Principia Mathematica Philosophia Naturalis. Lon- don: Will. & Jno. Innys, Printers to the Royal Society. Newton, I. (1730). Opticks. Or, A Treatise of the Reflections, Refrac- tions, Inflections and Colours of Light. London: Printed for William Innys at the Westend of St. Paul’s. Newton, I. (1999). The Principia. Mathematical Principles of Natural Philosophy. Translated by B. I. Cohen and A. Whitman. Berkeley: University of California Press.” Newton, I. (2004). De Gravitatione. In A. Janiak (Ed.), Philosophical Writings (pp.12-39). Cambridge: Cambridge University Press. Plaaß, P. (1994). Kant’s Theory of Natural Science. Translation, Ana- lytic Introduction and Commtary by A. E. Miller and M. G. Miller. Dordrecht: Kluwer Academic Publisher. Pollok, K. (1997). “Einleitung” and “Anmerkung des Herausgebers”. In K. Pollok (Ed.), Metaphysische Anfangsgründe der Naturwissen- schaft (pp. IX-LXII and 127-149). Hamburg: Meiner. Pollok, K. (2000). Kants “Metaphysische Anfangsgründe der Naturwis- senschaft”. Ein kritischer Kommentar. Hamburg: Felix Meiner Ver- lag. Pulte, H. (1999). “… sondern Empirismus und Speculation sich ver- binden sollen”. Historiographische Überlegungen zur bisherigen Re- zeption des wissenschafttheoretischen und naturphilosophischen Werkes von J. F. Fries und einige Gründe für dessen Neubewertung. In W. Hogrebe, & K. Herrmann (Eds.), Jakob Friedrich Fries, Philosoph, Naturwissenschaftler und Mathematiker (pp. 57-93). Frankfurt am Main: Peter Lang. Pulte, H. (2005). Axiomatik und Empirie. eine wissenschaftstheorie- geschichtliche Untersuchung zur Mathematischen Naturphilosophie von Newton bis Neumann. Darmstadt: Wissenschaftliche Buchge- sellschaft Pulte, H. (2007). Kant, Fries and the Expanding Universe of Science. In M. Friedman, & A. Nordmann (Ed.), The Kantian Legacy in the Ni- neteenth-Century Science (pp. 101-121). Cambridge, Mass.: The MIT Press. Sachs-Hombach, K. (1999). Ist Fries’s Erkenntnistheorie psychologi- stisch. In W. Hogrebe, & K. Herrmann (Ed s .), Jakob Friedrich Fries, E. GÖRG Open Access Philoso ph, Natu rwi ssensc haft ler und M athematiker (pp. 119-139). Frank- furt am Main: Peter Lang. Schubring, G. (1999). Philosophie der Mathematik bei Fries. In W. Ho- grebe, & K. Herrmann (Eds.), Jakob Friedrich Fries, Philosoph, Naturwissenschaftler und Mathematiker (pp. 175-193). Frankfurt am Main: Peter Lang. van Zantwijk, T. (2009). Heuristik und Wahrscheinlichkeit in der lo- gischen Methodenlehre. Padaborn: Mentis. van Zantwijk, T. (2010). Fries on Con sequencetypes in Natu ral Science. In O. Breidbach, & A. Burwick (Eds.), Physics around 1800. Arts, Science or Philosophy? New York: Edwin Mellen Press (in Print). Wundt, M. (1932). Die Philosop hie an der Universität Jena. Jena: Fis- cher.
|