Advances in Historical Studies
2014. Vol.3, No.1, 2-11
Published Online February 2014 in SciRes (http://www.scirp.org/journal/ahs) http://dx.doi.org/10.4236/ahs.2014.31002
Open Access 2
Three Criticisms of Newton’s Inductive Argument in the Principia
Nicholas Maxwell
Science and Technology Studies, University College London, London, UK
Received April 30th, 2013; revised June 4th, 2013; accepted June 10th, 2013
Copyright © 2014 Nicholas Maxwell. This is an open access article distributed under the Creative Commons
Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the
original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights ©
2014 are reserved for SCIRP and the owner of the intellectual property Nicholas Maxwell. All Copyright ©
2014 are guarded by law and by SCIRP as a guardian.
In this paper, I discuss how Newton’s inductive argument of the Principia can be defended against criti-
cisms leveled against it by Duhem, Popper and myself. I argue that Duhem’s and Popper’s criticisms can
be countered, but mine cannot. It requires that we reconsider, not just Newton’s inductive argument in the
Principia, but also the nature of science more generally. The methods of science, whether conceived
along inductivist or hypothetico-deductivist lines, make implicit metaphysical presuppositions which rig-
orously require us to make them explicit within science so that they can be critically assessed, alternatives
being developed and assessed, in the hope that they can be improved. Despite claiming to derive his law
of gravitation by induction from phenomena without resource to hypotheses, Newton does nevertheless
acknowledge in the Principia that his rules of reasoning make metaphysical presuppositions. To this ex-
tent, Newton has a more enlightened view of scientific method than most 20th and 21st century scientists
and historians and philosophers of science.
Keywords: Newton; Principia; Newton’s Inductive Argument; Three Criticisms; Duhem; Popper;
Metaphysical Presuppositions of Scientific Method; Theoretical Unity; New Conception of
Science
The Inductive Argument of the Principia
In his Aim and Structure of Physical Theory, first published
in 1906, Pierre Duhem ostensibly demolished Isaac Newton’s
inductive argument of his Principia, which claimed to have
derived by induction the law of universal gravitation from the
phenomena1. Duhem’s criticism was echoed, and perhaps
strengthened by Karl Popper. In this paper I make a suggestion
as to how Duhem’s and Popper’s criticism may be countered.
Implicit in work I have published over a number of decades
there is, however, another criticism of Newton’s argument
which is more general, and applies to all conceptions of scien-
tific method which specify empirical, and possibly simplicity,
considerations that govern acceptance of laws and theories in
physics, but which deny, or fail to acknowledge, that meta-
physical hypotheses play a crucial role. This criticism is more
difficult to counter.
In the Principia, Newton proceeds as follows. In Book 1, af-
ter defining crucial notions such as “quantity of motion”, New-
ton formulates the following three laws of motion, the basis for
classical mechanics2:
1) Every body continues in its state of rest, or of uniform
motion in a right line, unless it is compelled to change that state
by forces impressed upon it.
2) The change of motion is proportional to the motive force
impressed; and is made in the direction of the right line in
which that force is impressed.
3) To every action there is always an opposed and equal re-
action or the mutual actions of two bodies upon each other are
always equal, and directed to contrary parts.
Newton then goes on in Book 1 to prove a great number of
propositions and theorems, many, but by no means all, related
to the task of establishing his universal law of gravitation and
using it to explain the System of the World—that is, the solar
system—to be taken up in Book 3. Thus the first theorem
proves that a body attracted by a force to a fixed point moves in
such a way that the line joining the body to the fixed point
sweeps out equal areas in equal times—echoes of Kepler’s 2nd
law! Theorem 2 established the converse: if a body moves so
that a line joining it to a fixed point sweeps out equal areas in
equal times then it is attracted to the fixed point by a force.
Proposition 11 establishes that a body moving in an ellipse
experiences a force directed at a focus of the ellipse, the
strength of the force being inversely proportional to the square
of the distance. Newton goes on to establish similar results for
bodies moving in hyperbolas and parabolas. He then goes on, in
proposition 17, to prove the converse of these results, namely
that if a body moves under the influence of a force directed
towards a fixed point, the force varies inversely as the square of
the distance, then the body will move in a conic section—an
ellipse, parabola or hyperbola.
Book 2 is in the main concerned with the motion of bodies
through fluids. It may have been written in part to refute Des-
cartes’ vortex theory of the solar system, according to which
1Duhem ((1962: pp. 190-195), first published in French as a series of articles
in 1904 and 1905, and as a book in 1906.
2Newton (1962: vol. 1, p. 13).

N. MAXWELL
Open Access 3
invisible swirling matter in space sweeps the planets round the
sun (a modified version of which was also held by Christiaan
Huygens).
Book 3, exploiting the results of Book 1, sets out to establish
Newton’s universal law of gravitation and explain the System
of the World. First, Newton makes explicit his conception of
what we would today call “scientific method” in what he calls
“Rules of Reasoning in Philosophy”:
Rule 1: We are to admit no more causes of natural things
than such as are both true and sufficient to explain their ap-
pearances.
Rule 2: Therefore to the same natural effects we must, as far
as possible, assign the same causes.
Rule 3: The qualities of bodies, which admit neither intensi-
fication nor remission of degrees, and which are found to be-
long to all bodies within the reach of our experiments, are to be
esteemed the universal qualities of all bodies whatsoever.
Rule 4: In experimental philosophy we are to look upon
propositions inferred by general induction from phenomena as
accurately or very nearly true, notwithstanding any contrary
hypothesis that may be imagined, till such time as other phe-
nomena occur, by which they may either be made more accu-
rate, or liable to exceptions3.
Newton goes on to specify six “phenomena”—six regulari-
ties of the solar system—that form the empirical basis for ar-
riving at the law of gravitation. These are that the moons of
Jupiter and Saturn obey Kepler’s 2nd and 3rd laws of planetary
motion, and so too do the planets other than the earth in their
motion round the sun; and our moon, in its motion round the
earth, obeys Kepler’s 2nd law.
Newton then goes on, in a number of propositions and theo-
rems, to establish his universal law of gravitation by means of
his laws of motion and mathematical theorems of Book I, and
the six phenomena just indicated—the above four rules of rea-
soning being appealed to at various points. Thus Newton first
proves, in Proposition 1, that the moons of Jupiter move subject
to a force directed towards the centre of the planet that is in-
versely proportional to the square of the distance to the centre
(i.e. F α 1/D2, where D is the distance from the centre of the
moon to the centre of Jupiter). He goes on to establish the same
for the moons of Saturn and, in Proposition 2, the same for the
planets (D in this case, of course, being the distance to the cen-
tre of the sun). The moon too is shown to obey the inverse
square law (in Proposition 3). Then, invoking rules 1 and 2,
Newton argues, in Proposition 4, that the force to which the
moon is subject is the force of gravity—the very same force we
feel on earth and call gravity, responsible for bodies falling near
the earth’s surface. Likewise (Proposition 5), the moons of
Jupiter are drawn towards Jupiter by the force of gravitation—
as are the moons of Saturn towards Saturn. And indeed “there is
a power of gravity tending towards all the planets”. “And”,
Newton goes on “since all attraction (by Law III) is mutual,
Jupiter will therefore gravitate towards all his satellites, Saturn
towards his, and the earth towards the moon, and the sun to-
wards the planets”. And “all the planets do gravitate towards
one another” which means, Newton points out, that Jupiter and
Saturn, when closest together, will sensibly disturb each other’s
motion, as the sun disturbs our moon’s motion, and the sun and
moon disturb our sea (causing the tides). Then (in Proposition
6), Newton sets out to establish that “all bodies gravitate to-
wards every planet”, weights of bodies, at any given distance
from the centre of the planet, being proportional to the quantity
matter (i.e. the mass). Newton then establishes that “there is a
power of gravity pertaining to all bodies, that is proportional to
several quantities of matter which they contain”. Then, in
Proposition 8, we have the theorem that two homogeneous
spheres attracting each other by gravitation, the weight of either
“will be inversely as the square of the distance between their
centres”. Newton then establishes that the centre of the solar
system is, not the centre of the sun, but rather the centre of
gravity of the solar system, the sun being somewhat in motion
with respect to this centre as it is tugged this way and that by
the gravitational attraction of the planets. Newton then derives
Kepler’s laws for the planets a priori as he puts it, the planets
only moving precisely in ellipses, however, if gravitational
forces between planets are neglected, and the sun is assumed
not to move4.
Newton goes on to derive various consequences from his law
of gravitation and what has been established so far. He dis-
cusses the flattening of the earth and other planets at the poles
because of their rotation; variation in weight at different lati-
tudes on earth; gravitational attraction of the moon and sun
producing the tides; the motion of the moon, affected by gravi-
tational attraction of both earth and sun—a difficult 3-body
problem which cannot be solved exactly; the motion of comets,
which are shown to be along conic sections (approximately
parabolas close to the sun)5.
It hardly needs to be said that what Newton does in the Prin-
cipia is extraordinarily impressive. It really does seem that
Newton derives his universal law of gravitation from the phe-
nomena, just as he claimed he had done. First, there are the
purely mathematical theorems: bodies that move so at to obey
Kepler’s laws must be deflected from uniform motion in a
straight line by a force that varies inversely as the square of the
distance. Then, observation tells us that moons and planets do
actually move so as to obey Kepler’s laws. Therefore they must
be subject to a force that varies inversely as the square of the
distance. And since we can move, by degrees, from the motion
of stone thrown on earth to the motion of the moon round the
earth, this force must be the force of gravitation, of which we
are so familiar here on earth. Granted that every body in the
universe gravitationally attracts every other body, it is clear that
the motions of the moons and planets must deviate slightly
from perfect Keplerian motion due to mutual gravitational at-
traction—the final, devastatingly convincing evidence in sup-
port of Newtonian theory.
Duhem’s Criticism of Newton
But all this is, on the face of it, decisively demolished by Pi-
erre Duhem. In 1906 in his The Aim and Structure of Physical
Theory Duhem pointed out that Newton could not possibly
have derived his law from the phenomena since, as Newton had
himself pointed out, his law revealed that the phenomena are
not correct. Because planets attract each other and the sun, Ke-
pler’s laws are not precisely obeyed. But what this means is that
the whole argument of the Principia is nothing more than a
reductio ad absurdum. Assume A (the laws of motion and Ke-
3Newton (1962: Vol. 2, pp. 398-400). These rules were modified, and even
added to, by Newton in successive editions of the Principia.
4All this is established in the first 24 pages of Book 3 of the Principia: see
N
ewton (1962: Vol. 2, pp. 399-422).
5For a recent, impressive and very detailed account of Newton’s inductive
argument in the Principia see Harper (2011).

N. MAXWELL
Open Access 4
pler’s laws); derive B (Kepler’s laws are false). B contradicts A,
therefore A is false. Newton’s great argument is reduced to the
demonstration that his initial assumptions amount to a contra-
diction—not what Newton claimed to prove at all6.
Duhem’s argument is pretty devastating. But one feels that it
somehow does not quite do justice to the sophistication of
Newton’s argument. This argument is not, after all, a straight-
forwardly deductive argument. It is an argument that comes in a
number of stages, some deductive, some inductive. And that the
conclusion—the universal law of gravitation—leads to a cor-
rection in the premises—Kepler’s laws—far from sabotaging
the whole validity of the argument, is actually one of the great
strengths of the argument, and provides additional strong
grounds for holding that the law of gravitation should be ac-
cepted. It is almost, one might say, the clinching argument.
How can one salvage Newton’s great argument from Du-
hem’s attack? It can be done, perhaps, along the following lines.
Newton argues that planets that move around a fixed sun in
orbits that obey Kepler’s laws are subject to a force that varies
inversely as the square of the distance. We may take that part of
the argument as deductive and valid. We then contribute the
third law of motion (every force has its equal and opposite
force) and, eventually, the law that every body attracts every
other as the inverse square of the distance—arrived at by induc-
tion. This means that the planets do not move around the sun in
accordance, precisely, with Kepler’s laws (because they attract
the sun and each other). Does this mean the deductive part of
this argument is invalid? No, it does not. The argument is valid,
but the premises of the argument are false. If the planets move
in Keplerian orbits round a fixed sun, then indeed, quite validly,
they are subject to the relevant force directed at the sun. It is
just that the sun is not fixed, the planets attract it, and attract
each other. So, the premise of the argument is false, but this
deductive part of the argument is valid.
We can now go on to consider: Does the falsity of the prem-
ise—the strict falsity of Kepler’s laws—invalidate Newton’s
entire argument? Well, hardly. Because if we feed in the more
precise, the true (or very nearly true) versions of the premises—
orbits very nearly Keplerian, but with deviations or “perturba-
tions”, due to mutual gravitational attraction of heavenly bodies,
and run the entire argument as before, deductive stages plus
inductive stages, with these new corrected premises, no Duhem
inconsistency between premises and conclusion emerges at all.
The whole argument becomes self-consistent.
It is the possibility of correcting the entire argument in this
fashion, as a result of what has been learned from the first run-
through of the argument, that salvages Newton’s whole argu-
ment, deductive and inductive, from Duhem’s apparently dev-
astating attack.
If Newton’s argument was wholly and entirely deductive in
character, Duhem’s criticism would be more serious. In fact the
argument has a number of stages to it, some deductive, some
inductive, the conclusion having far more content in it than the
premises, in that the universal law of gravitation applies to all
bodies everywhere, at all times and places, and not just to the
bodies of the solar system. It is this inductive, content-in-
creasing character of the argument which introduces the possi-
bility that the conclusion may contradict the initial assumptions,
something which is wholly prohibited in a purely deductive
argument.
A deductive argument is valid if it reveals that it is not possi-
ble for the premise to be true and the conclusion false. That is
the only requirement. In order to procure validity, the conclu-
sion must be, as it were, contained in the premise. The conclu-
sion must not assert anything in addition to what the premise
asserts for, if it did, then it would be possible for that extra bit
to be false even though the premise is true, and then the argu-
ment would violate the only requirement for validity.
But none of this applies to inductive arguments. The whole
point of an inductive argument is to arrive at a universal law or
theory from particular observations, experimental results or
regularities. Newton exhibits the pattern of an inductive argu-
ment very well. In the case of an inductive argument, then, the
conclusion asserts far, far more than the premise, and so it is
quite possible that the premise might be true and the conclusion
false.
Duhem noticed that Newton suffers from a somewhat more
serious flaw: the conclusion is actually inconsistent with the
premise. One might have thought that it would be reasonable to
hold that an inductive argument can only be acceptable as an
inductive argument if the premise can be deductively derived
from the conclusion—or at least that conclusion and premise
are consistent with one another. But, if we take Newton’s in-
ductive argument to be acceptable, then we have to acknowl-
edge that these requirements for acceptability are too strong.
We can, however, demand a slightly weaker version of the
above requirement. An inductive argument which is such that
the conclusion is incompatible with the premise is only accept-
able if a modified version of the premise can be derived from
the conclusion (and, possibly, other relevant propositions), and
this is found to be more accurate by observation or experiment
than the original premise. (This is put forward as a necessary,
but not a sufficient, requirement for acceptability.)
Newton’s inductive argument in the Principia satisfies this
weaker requirement for an inductive argument to be acceptable,
and it is on that ground that Duhem’s criticism is to be rebut-
ted7.
But this reason for rejecting Duhem’s criticism does seem
somewhat formal and pedantic. That Newton’s theory corrects
the phenomena upon which it is inductively based is treated as
a problem that can be overcome when it ought to be treated as
an immense success of the theory, that provides especially
strong grounds for its acceptance. Almost everyone agrees that
the capacity of a new theory to predict new phenomena, or to
predict hitherto unsuspected inaccuracies in accepted laws,
provides especially strong grounds for accepting the new theory.
The above rebuttal of Duhem’s criticism does not seem to do
justice to this widely accepted feature of scientific method and
rationality.
Perhaps this cannot be done within the constraints of an in-
ductive construal of scientific method. It may be that we need
to adopt a hypothetico-deductive, or falsificationist, approach to
scientific method in order to do justice to the way a new theory
receives especially strong grounds for acceptance from cor-
recting empirical laws upon which it is ostensibly based. Let us
look at Popper’s criticism of Newton, and induction.
Popper’s Criticism of Newton
Karl Popper reiterated Duhem’s criticism of Newton’s induc-
6See Note 1.
7Harper (2011: pp. 127-130), also rejects Duhem’s criticism of Newton, but
not on quite the same grounds as suggested here.

N. MAXWELL
Open Access 5
tive argument and, in some respects, extended it. Popper points
out that Galileo’s law that freely falling bodies fall with con-
stant acceleration is contradicted by Newton’s law of gravita-
tion (plus laws of motion). As a body falls, it draws closer to
the centre of the earth, the force due to gravity increases
slightly, and so the acceleration increases slightly too8. This
Popperian extension of Duhem’s criticism seems a bit beside
the point as Newton does not include Galileo’s law among his
“phenomena”. He alludes to it, for example in proposition 6 of
Book 39, but only in the valid form that bodies fall equal dis-
tances in equal times (which does not require constant accelera-
tion).
Popper would also, however, criticize Newton on rather dif-
ferent and much more general grounds (grounds with which
Duhem might not have agreed). Popper argued that no induc-
tive argument is acceptable, whether its conclusions are com-
patible with its premises or not; and so Newton’s inductive
argument is not acceptable either, in whatever form. It might
seem that there is not much difference between induction and
hypothetico-deductivism, as long as inductivism makes no
claims to establish laws and theories with certainty, or with
some degree of probability. Any inductive argument for a the-
ory T could, it seems, be reformulated as a hypothetico-deduc-
tive reason for accepting T, and vice versa. Both involve ac-
cepting T in the light of evidence that can be derived from T
(ignoring the case of evidence contradicting T). Popper would
have disagreed. He would argue as follows. In order to assess
the acceptability of a law or theory in the light of evidence it is
essential to know whether the evidence has been obtained to
test severely the law or theory. If the theory has been subjected
to a programme of severe attempted falsification, and has sur-
vived, it deserves to be tentatively accepted; if it has not, it does
not. No inductive argument can capture this vital dimension of
severe attempted falsification, and hence no inductive argument
can provide acceptable grounds for accepting a law or theory in
science10.
Instead of construing scientific method as a process of arriv-
ing at theories by induction from phenomena we need rather to
conceive of it as a process of proposing ever more bold, ever
more falsifiable, conjectures which are then subjected to sus-
tained, fierce attempted empirical refutation. Observations and
experiments need to be understood in a theoretical context, as a
part of the attempt to falsify theories, or decide between com-
peting theories, and not as data gathered in a theoretically neu-
tral context, to be used subsequently as premises for inductive
arguments deployed to establish new theories. Newton’s Prin-
cipia would have been a more scientifically rigorous book if it
had put forward the three laws of motion and the law of uni-
versal gravitation as pure conjectures from which a wealth of
empirically successful predictions are derived. That some of
these predictions correct hitherto accepted empirical laws poses
no problem whatsoever, and is quite straightforwardly a great
success for the theory, in that it indicates that what the theory
asserts to exist—every particle of matter attracted by every
other particle of matter in accordance with the law of gravita-
tion—really does obtain in Nature11.
Newton did not proceed in this way, it may be argued, for
purely personal reasons. He hated controversy. If he had for-
mulated the Principia as a hypothetico-deductive treatise, in-
evitably he would have invited a torrent of criticism. The entire
argument would have been attacked as entirely invalid. It has
the form: If P then Q; but Q; therefore P. Newton’s contempo-
raries knew very well that this is an invalid mode of argument.
That endlessly many true consequences can be derived from
Newton’s laws does not mean that those laws are true. The
Principia would have also been attacked on the grounds that it
is based on an absurdity: a purely speculative law which postu-
lates a force—the force of gravity—that acts at a distance
through empty space.
Well aware of the highly controversial character of what he
sought to establish, Newton formulated his Principia in such a
way that criticism was, as far as possible, forestalled from the
outset. The phenomena were undeniable. The mathematical
theorems were undeniable. Newton did not put forward conjec-
tures. He derived his law of gravitation from the phenomena by
means of a rigorous process of induction.
As it was, the Principia did receive criticism. Thus Huygens
in a letter to Leibniz declared “Concerning the Cause of the
flux given by M. Newton, I am by no means satisfied [by it],
nor by all the other theories he builds upon his Principle of At-
traction, which seems to me absurd. I have often wondered how
he could have given himself all the trouble of making such a
number of investigations and difficult calculations that have no
other foundation than this very principle”12. Huygens in fact
agreed that Newton had shown that planets move so as to be
subject to a force that varies inversely with the square of the
distance to the sun. What he rejected was the Newtonian thesis
that every particle of matter attracts every other particle in the
universe in accordance with Newton’s law of gravitation13.
Can Newton’s inductive argument be rescued from the gen-
eral Popperian criticism indicated above? A case can certainly
be made out that Newton’s argument for his universal law of
gravitation would have been far less persuasive, in the context
in which it was put forward, if it had been couched in a hy-
pothetico-deductive form. The deductive-inductive argument
that Newton in fact spelled out in the Principia had an aston-
ishing impact. It led to the view among Newton’s contempo-
raries and successors that something quite unprecedented had
been achieved: secure knowledge of the inner workings of na-
ture had almost miraculously been acquired for the first time in
the history of humanity. Natural philosophy now had a method
to follow which led undeniably to authentic knowledge: New-
ton’s deductive and inductive methodology. Those who fol-
lowed Newton—Euler, Lagrange, Laplace, and many others-
could be confident that the Principia provided a secure basis for
elaboration and development. Newton’s deductive-inductive
argument created an intellectual atmosphere which made it
possible for something like the puzzle solving of Kuhnian nor-
mal science to ensue—no doubt required if classical physics
was to be developed to reveal its full, extraordinary theoretical
and empirical scope and success. The subsequent success of
Newtonian science owed much, it could be argued, to the fact
that Newton formulated his argument for his universal law of
gravitation in its actual deductive-inductive form, as opposed to
a hypothetico-deductive form.
According to the Popperian criticism of induction indicated
8Popper (1972: ch. 5).
9Newton (1962: Vol. 2, p. 411).
10Popper (1959; 1963).
11It is not especially anachronistic to suggest that Newton might have for-
mulated the Principia in this hypothetico-deductive mode. Galileo put for-
ward some of his discoveries in this way—for example his theory of sun-
spots, and his theory of free fall.
12Koyré (1965: pp. 117-118).
13See Harper (2011: p. 205).

N. MAXWELL
Open Access 6
above, hypothetico-deductivism encourages criticism and at-
tempted falsification, and thus encourages the growth of know-
ledge, whereas inductivism creates the false impression that
what has been established inductively constitutes secure know-
ledge, and thus does not require criticism, and does not need to
be subjected to attempted empirical refutation. In thus inhibit-
ing criticism and attempted falsification, inductivism will tend
to inhibit the growth of knowledge.
But the historical record does not seem to provide grounds
for holding that any of this actually occurred. Newtonian theory
was not protected from empirical refutation as a result of natu-
ral philosophers adopting a too reverential attitude towards the
theory—not at least until the discovery of the anomalous mo-
tion of Mercury in the 19th century. And in any case, in order
to subject a theory to attempted empirical falsification, what
matters is that empirical consequences are derived from the
theory and then put to the test of observation and experiment. It
does not matter much what attitude of mind those who do the
work have—inductive or hypothetico-deductive—as long as a
variety of empirical implications of the theory are unravelled,
and then tested observationally or experimentally. Those who
came after Newton most certainly did apply the theory to as
wide a range of phenomena as possible, thereby subjecting the
theory to severe empirical testing even if this was not explicitly
the intention.
The advance of classical physics after Newton was it seemed
helped by general acceptance of Newtonian inductivism, and
not retarded in the way Popper’s argument would seem to sug-
gest it ought to have been.
It might nevertheless be argued that there would have been
substantial benefits if Newton had put forward his law of gra-
vitation as a conjecture which predicts—and thus potentially
explains—a wealth of empirical phenomena. The whole subse-
quent conception of science would have been different. Instead
of science being conceived of as a massive, unassailable au-
thority providing knowledge securely established by eviden-
ce—as it tended to be viewed in the 19th and early 20th centu-
ries—science would have been understood to be the enterprise
of proposing bold, imaginative conjectures which are then sub-
jected to an onslaught of attempted empirical refutation and
severe criticism. Scientific knowledge is just our very best
guesses about the nature of things that have so far survived our
most ferocious attempts to overthrow them. Science would
have been more honest, more openly fallible, and such that it
had much to teach other areas of human life: politics, econom-
ics, even philosophy.
Third Argument Concerning the Metaphysical
Presuppositions of the Methods of Physics
So far I have argued that Duhem’s and Popper’s criticisms of
Newton’s deductive-inductive argument for his law of gravita-
tion in the Principia are not perhaps as devastating as one
might at first suppose. There is, however, another criticism of
Newton’s argument that really is devastating. This comes from
a line of argument I have developed in recent decades in a se-
ries of publications14. Granted that this argument is valid, not
only must we reject Newton’s claim to have derived his law of
gravitation from the phenomena by induction without resource
to hypotheses. We must also reject Duhem’s and Popper’s con-
ceptions of science as well. Indeed, we must reject all concep-
tions of scientific method, whether inductivist or hypothetico-
deductivist, which fail to acknowledge that metaphysical hy-
potheses play an essential and permanent role in science in the
context of acceptance of laws and theories.
My argument can be formulated as follows. Let T be any ac-
cepted fundamental physical theory—Newtonian theory, clas-
sical electrodynamics, quantum theory, general relativity, quan-
tum electrodynamics, quantum electroweak theory, quantum
chromodynamics, or the standard model. There are, to begin
with, infinitely many disunified rivals to T—T1, T2, … T∞—
that are just as empirically successful as T. In order to concoct
such a rival, T1 say, all we need to do is modify T in an entirely
ad hoc way for phenomena that occur after some future date.
Thus, if T is Newtonian theory (NT), NT1 might assert: every-
thing occurs as NT predicts until the first moment of 2050
(GMT) when an inverse cube law of gravitation comes into
operation: F = Gm1m2/d3. Infinitely may such disunified rivals
can be concocted by choosing infinitely many different future
times for an abrupt, arbitrary change of law. These theories will
no doubt be refuted as each date falls due, but infinitely many
will remain unrefuted15. We can also concoct endlessly many
disunified rivals to T by modifying the predictions of T for just
one kind of system that we have never observed. Thus, if T is,
as before, NT, then NT2 might assert: everything occurs as NT
predicts except for any system of pure gold spheres, each of
mass greater than 1000 tons, moving in a vacuum, centres no
more than 1000 miles apart, when Newton’s law becomes F =
Gm1m2/d4. Yet again, we may concoct further endlessly many
equally empirically successful disunified rivals to T by taking
any standard experiment that corroborates T and modifying it in
some trivial, irrelevant fashion—painting the apparatus purple,
for example, or sprinkling diamond dust in a circle around the
apparatus. We then modify T in an ad hoc way so that the mod-
ified theory, T3 say, agrees with T for all phenomena except for
the trivially modified experiment. For this experiment, not yet
performed, T3 predicts—whatever we choose. We may choose
endlessly many different outcomes, thus creating endlessly
many different modifications of T associated with this one tri-
vially modified experiment. On top of that, we can, of course,
trivially modify endlessly many further experiments, each of
which generates endlessly many further disunified rivals to
T.
Each of these equally empirically successful, disunified ri-
vals to T—T1, T2, … T∞—can now be modified further, so that
each becomes empirically more successful than T. Any ac-
cepted fundamental physical theory is almost bound to face
some empirical difficulties, and is thus, on the face of it, refuted
—by phenomena A. There will be phenomena, B, which come
within the scope of the theory but which cannot be predicted
14See Maxwell (1974; 1993; 1998; 2000; 2002; 2004; 2005; 2007, espe-
cially, ch. 14; 2011; 2013).
15The famous arguments of David Hume (1959) concerning causation have
long rendered familiar the point that, for all we can ever know for certain,
physical laws may, at some future time, abruptly change, or, to put the same
point in an equivalent way, given any physical theory, however empirically
successful, there will always be infinitely many rival theories that fit all
available evidence just as well but which postulate an abrupt change in
p
hysical laws at some future time. What I go on to argue in the text is that
these “Humean” theories, as we may call them, that postulate an abrupt
change in physical law at some future time are just special cases of a much
wider class of disunified theories that postulate an abrupt change in physical
law as conditions change in some way other than time, such as kind of sys-
tem, or experimental conditions. And furthermore, I argue, all these disuni-
fied theories can be further doctored to be empirically more successfulthan
the theories we accept.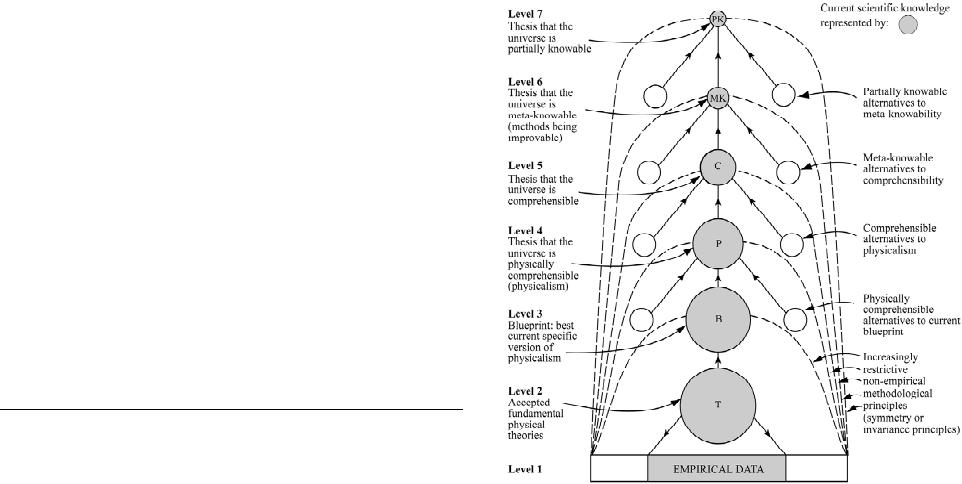

N. MAXWELL
Open Access 7
because the equations of the theory cannot (as yet) be solved.
And there will be other phenomena (C) that fall outside the
scope of the theory altogether. We can now take any one of the
disunified rivals to T, T1 say, and modify it further so that the
new theory, T1
*, differs further from T in predicting, in an en-
tirely ad hoc way, that phenomena A, B and C occur in accor-
dance with empirically established laws LA, LB and LC. T1
*
successfully predicts all that T has successfully predicted; T1
*
successfully predicts phenomena A that ostensibly refute T; and
T1
* successfully predicts phenomena B and C that T fails to
predict. On empirical grounds alone, T1
* is clearly more suc-
cessful and better corroborated, than T. And all this can be
repeated as far as all the other disunified rivals of T are con-
cerned, to generate infinitely many empirically more successful
disunified rivals to T: T1
*, T2 *, … T∞ *16.
But even though all of T1
*, T2 *, … T∞ * are more successful
empirically than T, they are all, quite correctly, ignored by
physics because they are all horribly disunified17. They postu-
late different laws for different phenomena in a wholly ad hoc
fashion, and are just assumed to be false. But this means phys-
ics makes a big, implicit assumption about the universe: it is
such that all such grossly disunified, “patchwork quilt” theories
are false.
If physicists only ever accepted theories that postulate atoms
even though empirically more successful rival theories are
available that postulate other entities such as fields, it would
surely be quite clear: physicists implicitly assume that the uni-
verse is such that all theories that postulate entities other than
atoms are false. Just the same holds in connection with unified
theories. That physicists only ever accept unified theories even
though endlessly many empirically more successful, disunified
rival theories are available means that physics implicitly as-
sumes that the universe is such that all such disunified theories
are false.
In accepting the (more or less) unified theories that it does
accept—Newtonian theory, classical electrodynamics and the
rest—physics thereby adopts a big, highly problematic meta-
physical hypothesis, H, about the nature of the universe: it is
such that all rival, grossly disunified, “patchwork quilt” but
empirically more successful theories are false. H, though a
metaphysical hypothesis, is nevertheless a permanent, even if
generally unacknowledged, item of theoretical knowledge.
Theories that clash with it, even though empirically more suc-
cessful than accepted physical theories, are rejected—or rather,
are not even considered for acceptance. Whenever a fundamen-
tal physical theory is accepted, endlessly many empirically
more successful rivals, easily formulated, are not even consid-
ered just because, in effect, they clash with H. Thus H is a per-
manent item of theoretical knowledge in physics, more securely
established in scientific practice indeed than any physical the-
ory. Physical theories tend eventually to be shown to be false,
but H persists through theoretical revolutions in physics18.
Nevertheless, H is a hypothesis, a pure conjecture. How can
one make sense of the idea that science is rational and delivers
authentic knowledge if the whole enterprise depends crucially
on accepting such an unsupported hypothesis as a secure item
of scientific knowledge—a hypothesis that exercises a major
influence over what theories are accepted and rejected in phys-
ics?
Aim-Oriented Empiricism
In order to answer this question, we need to adopt a concep-
tion of science that I have called “aim-oriented empiricism”.
Precisely because H is a substantial assertion about the nature
of the universe, an assertion that, though purely conjectural in
character, nevertheless exercises a major influence over what
theories are accepted and rejected, even to the extent of over-
riding empirical considerations, it needs to be made explicit
within physics so that it can be critically assessed, rival hy-
potheses if possible being developed and assessed, in the hope
that H can be improved on. We need a new conception of sci-
ence, I have argued, which represents the metaphysical hy-
potheses of physics in the form of a hierarchy of hypotheses, as
one goes up the hierarchy hypotheses becoming less and less
substantial, and more nearly such that their truth is required for
science, or the pursuit of knowledge, to be possible at all. In
this way we create a relatively unproblematic framework of
hypotheses, and associated methodological rules, high up in the
hierarchy, within which much more substantial and problematic
hypotheses, and associated methodological rules, low down in
the hierarchy, can be critically assessed and, we may hope,
improved, in the light of the empirical success they lead to, and
other considerations: see Figure 1.
At the top there is the relatively insubstantial hypothesis that
the universe is such that we can acquire some knowledge of our
local circumstances. If this hypothesis is false, we will not be
able to acquire knowledge whatever we assume. We are justi-
fied in accepting this hypothesis permanently as a part of our
knowledge, even though we have no grounds for holding it to
be true. As we descend the hierarchy, the hypotheses become
Figure 1.
Aim-Oriented Empiricism (AOE).
16Even if no phenomena ostensibly refute T, each of T1*, T2*, … T∞
*is still
more successful empirically than T.
17For my account of theoretical unity, an account which emerges from the
argument expounded in the text, see Maxwell (1998, Chs. 3 and 4; 2004,
Appendix, Section 2; 2007: pp. 373-386; 2013, Section 4).
18For expositions of this argument see Maxwell (1974: Part 1; 1993: Part 1;
1998: ch. 2; 2000; 2002; 2004, ch. 1; 2005; 2011; 2013.

N. MAXWELL
Open Access 8
increasingly substantial and thus increasingly likely to be false.
At level 6 there is the more substantial hypothesis that the uni-
verse is such that there is some rationally discoverable thesis
about the nature of the universe which, if true and if accepted,
makes it possible progressively to improve methods for the
improvement of knowledge. “Rationally discoverable”, here,
means at least that the thesis is not an arbitrary choice from
infinitely many analogous theses. At level 5 we have the even
more substantial hypothesis that the universe is comprehensible
in some way or other, whether physically or in some other way.
This hypothesis asserts that the universe is such that there is
something (God, tribe of gods, cosmic goal, physical entity,
cosmic programme or whatever), which exists everywhere in an
unchanging form and which, in some sense, determines or is
responsible for everything that changes (all change and diver-
sity in the world in principle being explicable and understand-
able in terms of the underlying unchanging something). A uni-
verse of this type deserves to be called “comprehensible” be-
cause it is such that everything that occurs, all change and di-
versity, can in principle be explained and understood as being
the outcome of the operations of the one underlying something,
present throughout all phenomena. At level 4 we have the still
more substantial hypothesis that the universe is physically
comprehensible in some way or other. This asserts that the uni-
verse is made up one unified self-interacting physical entity (or
one kind of entity), all change and diversity being in principle
explicable in terms of this entity. What this amounts to is that
the universe is such that some yet-to-be-discovered unified
physical theory of everything is true. At Level 3, we have an
even more substantial hypothesis, the best, currently available
specific idea as to how the universe is physically comprehensi-
ble. This asserts that everything is made of some specific kind
of physical entity: corpuscle, point-particle, classical field, quan-
tum field, convoluted space-time, quantum string, or whatever.
Given the historical record of dramatically changing ideas at
this level, and given the relatively highly specific and substan-
tial character of successive hypotheses made at this level, we
can be reasonably confident that the best hypothesis available at
any stage in the development of physics at this level will be
false, and will need future revision. Here, ideas evolve with
evolving knowledge. At Level 2 there are the accepted funda-
mental theories of physics, currently general relativity and the
standard model. Here, if anything, we can be even more confi-
dent that current theories are false, despite their immense em-
pirical success. This confidence comes partly from the vast
empirical content of these theories, and partly from the histori-
cal record. The greater the content of a proposition the more
likely it is to be false; the fundamental theories of physics, gen-
eral relativity and the standard model have such vast empirical
content that this in itself almost guarantees falsity. And the
historical record backs this up; Kepler’s laws of planetary mo-
tion, and Galileo’s laws of terrestrial motion are corrected by
Newtonian theory, which is in turn corrected by special and
general relativity; classical physics is corrected by quantum
theory, in turn corrected by relativistic quantum theory, quan-
tum field theory and the standard model. Each new theory in
physics reveals that predecessors are false. Indeed, if the Level
4 hypothesis is correct, then all current physical theories are
false, since this hypothesis asserts that the true physical theory
of everything is unified, and the totality of current fundamental
physical theory, general relativity plus the standard model, is
notoriously disunified. Finally, at Level 1 there are accepted
empirical data, low level, corroborated, empirical laws19.
The idea is to separate out what is most likely to be true, and
not in need of revision, at and near the top of the hierarchy,
from what is most likely to be false, and most in need of criti-
cism and revision, near the bottom of the hierarchy. Evidence,
at Level 1, and hypotheses high up in the hierarchy, are rather
firmly accepted as a part of theoretical knowledge in physics, as
being most likely to be true (although still open to revision):
this is then used to criticize, and to try to improve, hypotheses
at Levels 2 and 3 (and perhaps 4), where falsity is most likely to
be located.
In order to be acceptable, an hypothesis at any level from 6
to 3 must (as far as possible) be compatible with, and a special
case of, the hypothesis above in the hierarchy; at the same time
it must be (or promise to be) empirically fruitful in the sense
that successive accepted physical theories increasingly suc-
cessfully accord with (or exemplify) the hypothesis. At Level 2,
those physical theories are accepted which are sufficiently (a)
empirically successful and (b) in accord with the best available
hypothesis at Level 3 (or Level 4). Corresponding to each hy-
pothesis, at any level from 7 to 3, there is a methodological
principle, represented by sloping dotted lines in the diagram,
requiring that hypotheses lower down in the hierarchy are
compatible with the given hypothesis.
When theoretical physics has completed its central task, and
the true theory of everything, T, has been discovered, then T
will (in principle) successfully predict all empirical phenomena
at Level 1, and will entail the hypothesis at Level 3, which will
in turn entail the hypothesis at Level 4, and so on up the hierar-
chy. As it is, physics has not completed its task, T has not (yet)
been discovered, and we are ignorant of the nature of the uni-
verse. This ignorance is reflected in clashes between theses at
different levels of aim-oriented empiricism (AOE). There are
clashes between Levels 1 and 2, 2 and 3, and 3 and 4. And the
two fundamental theories at Level 2, the standard model and
general relativity, clash as well. The attempt to resolve these
clashes drives physics forward.
In seeking to resolve clashes between levels, influences can
go in both directions. Thus, given a clash between Levels 1 and
2, this may lead to the modification, or replacement of the rele-
vant theory at Level 2; but, on the other hand, it may lead to the
discovery that the relevant experimental result is not correct for
any of a number of possible reasons, and needs to be modified.
In general, however, such a clash leads to the rejection of the
level 2 theory rather than the level 1 experimental result; the
latter are held onto more firmly than the former, in part because
experimental results have vastly less empirical content than
theories, in part because of our confidence in the results of ob-
servation and direct experimental manipulation (especially after
repetition and expert critical examination). Again, given a clash
between Levels 2 and 3, this may lead to the rejection of the
19This hierarchical conception of scientific method seems first to have been
expounded in Maxwell (1974). It was further elaborated in Maxwell (1993).
A more elaborate version still is expounded and defended in great detail in
Maxwell (1998). For a more detailed defence of the version indicated here,
see Maxwell (2004: chs. 1 and 2, and appendix). Maxwell (2005) argues that
this view is a sort of synthesis of the views of Popper, Kuhn and Lakatos,
but an improvement over the views of all three. Maxwell (2007: ch. 14)
gives a detailed exposition of aim-oriented empiricism, and argues, in some
detail, that the view succeeds in solving major problems in the philosophy o
f
science, including the problems of induction, simplicity and verisimilitude.
The most recent, and possibly the best, exposition and defense of aim-ori-
ented empiricism is Maxwell (2013).

N. MAXWELL
Open Access 9
relevant Level 2 theory (because it is disunified, ad hoc, at odds
with the current metaphysics of physics); but, on the other hand,
it may lead to the rejection of the Level 3 hypothesis and the
adoption, instead, of a new hypothesis (as has happened a
number of times in the history of physics). The rejection of the
current Level 3 hypothesis is likely to take place if the Level 2
theory, which clashes with it, is highly successful empirically,
and furthermore has the effect of increasing unity in the totality
of fundamental physical theory overall, so that clashes between
Levels 2 and 4 are decreased. In general, however, clashes be-
tween Levels 2 and 3 are resolved by the rejection or modifica-
tion of theories at Level 2 rather than the assumption at Level 3,
in part because of the vastly greater empirical content of Level
2 theories, in part because of the empirical fruitfulness of the
Level 3 assumption (in the sense indicated above).
It is conceivable that the clash between Level 2 theories and
the Level 4 hypothesis might lead to the revision of the latter
rather than the former. This happened when Galileo rejected the
then current level 4 hypothesis of Aristotelianism, and replaced
it with the idea that “the book of nature is written in the lan-
guage of mathematics” (an early precursor of our current Level
4 hypothesis). The whole idea, however, is that as we go up the
hierarchy of hypotheses we are increasingly unlikely to en-
counter error, and the need for revision. The higher up we go,
the more firmly hypotheses are upheld, the more resistance
there is to modification.
The idea of representing the metaphysical presuppositions of
physics (concerning the nature of the universe) as a hierarchy of
theses, increasingly insubstantial as one goes up the hierarchy,
gains some support from the fact that something somewhat
similar exists informally at the empirical level—Level 1 of the
figure—and for much the same reason. There are, at the lowest
level, the results of experiments performed at specific times and
places. Then, above these, there are low-level experimental
laws, asserting that each experimental result is a repeatable
effect. Next up, there are empirical laws such as Hooke’s law,
Ohm’s law or the gas laws. Above these there are such physical
laws as those of electrostatics or of thermodynamics. And
above these there are theories which have been refuted, but
which can be “derived”, when appropriate limits are taken,
from accepted fundamental theory—as Newtonian theory can
be “derived” from general relativity. This informal hierarchy at
the empirical level exists for the same reason we need the hier-
archy at the metaphysical level: so that relatively contentless
and secure theses (at the bottom of the empirical hierarchy)
may be distinguished from more contentful and insecure theses
(further up the hierarchy) to facilitate pinpointing what needs to
be revised, and how, should the need for revision arise. That
such a hierarchy exists at the empirical level provides some
support for my claim that we need to adopt such a hierarchy at
the metaphysical level.
AOE, as depicted in Figure 1, provides physics with a me-
ta-methodology which facilitates improvement of the meta-
physical hypotheses, and associated methods, as physics ad-
vances, in the light of which seem to be the most fruitful em-
pirically, and other considerations. As knowledge in physics
improves, so metaphysical hypotheses and methods improve as
well or, in other words, we improve knowledge about how to
improve knowledge. There is something like positive feedback
between improving knowledge of the universe, and improving
aims and methods, improving knowledge about how to improve
knowledge. Everyone would acknowledge that this kind of
positive feedback goes on at the empirical level. New empirical
knowledge can lead to new methods, via the development of
new instruments, new experimental techniques, which in turn
lead to further acquisition of new knowledge. AOE provides
methods which facilitate such positive feedback at the meta-
physical and theoretical level as well. As we increase our scien-
tific knowledge and understanding of the universe, we increase
our knowledge of how to increase knowledge—the very nub of
scientific rationality which helps explain the explosive, and
apparently ever accelerating, growth of scientific knowledge.
We adapt the nature of science to what we find out about the
nature of the universe. All this has gone on in science to some
extent implicitly: what the adoption of AOE does is to make the
implicit explicit—science becoming even more successful as a
result.
I provide no grounds whatsoever for holding that the hy-
potheses at Levels 3 to 7 are true, probably true, or likely to be
true. What I do rather is to argue that these hypotheses are the
best that are available, granted the current state of knowledge in
physics, granted that some metaphysical hypothesis such as H
is implicit in the way physics persistently accepts (more or less)
unified theories even though endlessly many empirically more
successful disunified rivals are always available, and granted
that the aim of physics is to discover the truth about the nature
of the universe20. Hypotheses at Levels 7 and 6 are permanent
items of scientific knowledge. Arguments in support of accept-
ing these hypotheses make no appeal to the empirical success of
science. As one goes down the hierarchy, from Levels 5 to 3, it
becomes increasingly likely that the hypothesis at that level
may need to be revised.
My Criticism of Newton, and of Duhem
and Popper
One upshot of the above argument is the conclusion: no con-
ception of science can be tenable which denies, or fails to ac-
knowledge, that metaphysical hypotheses are a secure, perma-
nent part of scientific knowledge—hypotheses that are implicit
in those methods of physics which require sufficiently empiri-
cally successful and (more or less) unified theories to be ac-
cepted in preference to endlessly many empirically more suc-
cessful disunified rivals.
Both Duhem and Popper defend conceptions of science that
do deny that any such metaphysical hypotheses are an integral
part of scientific knowledge. These conceptions of science must
thus be rejected.
Newton claims in the Principia to have derived his law of
gravitation by induction from the phenomena without adopting
any hypotheses. He makes this clear in the General Scholium at
the end of the Principia. He says “whatever is not deduced
from the phenomena is to be called a hypothesis; and hypothe-
ses, whether metaphysical or physical, whether of occult quali-
ties or mechanical, have no place in experimental philosophy.
In this philosophy, particular propositions are inferred from the
phenomena, and afterwards rendered general by induction.
Thus it was that... the laws of motion and of gravitation were
discovered.”21
But Newton is wrong. In establishing his law of gravitation
by induction Newton cannot avoid adopting metaphysical hy-
20See Maxwell (1998: ch. 5; 2004: Appendix, Section 6; 2007: pp. 400-430;
2013: Sections 7 and 8).
21Newton (1962: Vol. 2, p. 547).

N. MAXWELL
Open Access 10
potheses. These are implicit in his four rules of reasoning in
philosophy, quoted above. Infinitely many rivals to Newton’s
law of gravitation are compatible with all the phenomena New-
ton cites in the Principia, as the argument of Section 4 above
makes clear. Some of these rivals would be even more empiri-
cally successful than Newtonian theory—for example, rivals
which modify Newtonian theory in a wholly ad hoc way so as
to predict the rotation of the perihelion of Mercury’s orbit, but
otherwise are precisely the same as Newtonian theory. These
infinitely many rivals are ruled out of court, not by evidence,
not by the phenomena, but by one or other, or all, of Newton’s
four rules of reasoning—by Newton’s conception of scientific
method, in other words.
One rival to Newton’s law of gravitation might postulate ad-
ditional forces which cancel themselves out for the solar system
but which do not for stars and other heavenly bodies far away,
which gravitate towards one another in accordance with a vari-
ety of laws. Such a theory (and endlessly many could be con-
cocted along these lines) successfully predicts all the phenom-
ena known to Newton that his theory predicts, but this theory is
to be excluded on the grounds that “we are to admit no more
causes of natural things than such as are ... sufficient to explain
their appearances” (Rule 1).
Another rival theory might agree with Newtonian theory as
far as the motions of the planets round the sun are concerned,
but postulate somewhat different laws of motion and law of
gravitation to predict and explain the motions of the moons of
Jupiter and Saturn. Such a theory is however to be excluded
because it violates the requirement that, “to the same natural
effects we must, as far as possible, assign the same causes”
(Rule 2).
And yet another rival theory might postulate that planets
other than the earth possess, not Newtonian inertial mass but
rather what might be called Galilean inertial mass so that, free
of any force, their inertial motion is to go round the sun in ac-
cordance with Kepler’s laws (or even orbits predicted by New-
tonian theory), there thus being no gravitational force between
these planets and the sun. Such a theory is however to be ig-
nored because, although it is compatible with the phenomena, it
violates the requirement that “the qualities of bodies ... which
are found to belong to all bodies within the reach of our ex-
periments, are to be esteemed the universal qualities of all bod-
ies whatsoever” (Rule 3).
Newton’s inductive argument of the Principia and his rules
of reasoning presuppose that terrestrial and astronomical phe-
nomena obey the same laws, so that one can make inductive in-
ferences from terrestrial to astronomical phenomena. But, given
the experimental knowledge available at the time of Newton,
this amounts to a substantial metaphysical hypothesis about the
nature of the universe. It is a hypothesis denied, for example, by
Aristotle. Generalizing inductively from experimental knowl-
edge of terrestrial phenomena to astronomical phenomena every-
where, at all times, presupposes implicitly the truth of this me-
taphysical hypothesis. Such inductive generalizing will only
meet with success if the hypothesis is true. In an Aristotelian
universe, it would lead one badly astray.
Newton’s claim to have established his law of gravitation
from the phenomena by induction without metaphysical hy-
potheses is thus untenable. Metaphysical hypotheses are im-
plicit in his four rules of reasoning, and these rules play a
crucial role in his inductive argument for his law of gravita-
tion.
But, as we saw in Section 4 above, this holds for all methods
of physics which exclude from consideration theories that are
disunified, ad hoc or complex, whatever their potential empiri-
cal success might be. 20th and 21st century views about scien-
tific method are just as vulnerable to the criticism as Newton’s
view is.
In some respects, indeed, Newton does better than contem-
porary scientists and philosophers of science. Most 20th and
21st scientists and philosophers of science acknowledge that
considerations of simplicity and unity play a role in physics in
deciding what theories are to be accepted and rejected, but nev-
ertheless would deny that this means physics adopts a substan-
tial, permanent metaphysical hypothesis about the nature of the
universe as a part of scientific knowledge. Newton is more
enlightened. He quite explicitly acknowledges that his rules of
reason do make assumptions about the nature of the universe.
He acknowledges this in his comments on the first three of his
four rules.
Thus, in connection with Rule 1, Newton declares “philoso-
phers say that Nature does nothing in vain, and more is in vain
when less will serve; for Nature is pleased with simplicity, and
affects not the pomp of superfluous causes”22. In other words, if
the universe were such that it delighted in complexity, and con-
stantly affected the pomp of superfluous causes, it would be
foolish and counterproductive to adopt Newton’s first rule of
inductive reasoning. In adopting the rule, and in accepting and
rejecting theories in accordance with it, we thereby adopt a
substantial hypothesis about the nature of the universe—and
Newton, unlike today’s scientists, was well aware of this fact.
Again, in connection with Rule 2, Newton comments “As to
respiration in a man and in a beast; the light of our culinary fire
and of the sun; the reflection of light in the earth, and in the
planets”23. But only in a certain kind of universe will the same
natural effects tend to have the same causes. It is not hard to
imagine possible universes where nothing of the kind holds,
and yet it is still possible for us to live, and to acquire knowl-
edge24. Newton is again more enlightened than most modern
scientists and philosophers of science in appreciating that his
second rule of inductive reasoning makes an assumption about
the nature of the universe which, if false, would render the rule
unproductive, the wrong rule to adopt.
And a similar point holds in connection with Newton’s much
lengthier comments on his third rule25. Here, too, Newton
makes clear that this rule makes a substantial assumption about
the nature of the universe, and will only be a sensible rule to
adopt in so far as the universe accords with what this assump-
tion says about it.
About the forth rule Newton says merely: “This rule we must
follow, that the argument of induction may not be evaded by
hypot heses” 26. This is a great disappointment after Newton’s
enlightened comments on the first three rules. Far from stress-
ing that in adopting and implementing Rule 4 we adopt a meta-
physical hypothesis about the nature of the universe, Newton
asserts almost the opposite: we must implement Rule 4 to en-
sure that we do not assume metaphysical hypotheses.
22Newton (1962: Vol. 2, p. 398).
23Newton (1962: Vol. 2, p. 398).
24See Maxwell (1998: ch. 5) for imaginative suggestions for possible uni-
verses in which science as we know it would not be possible because the
metaphysical hypotheses implicit in scientific method are false, but in which
life is possible, and the pursuit of knowledge can meet with success.
25See Newton (1962: Vol. 2, pp. 398-400).
26Newton (1962: Vol. 2, p. 400).

N. MAXWELL
Open Access 11
It is significant, however, that Rule 4 only appeared in the
third edition of the Principia published in 172627. It was, it
seems, an afterthought. Years after the publication of the first
edition, Newton may have managed to convince himself that no
metaphysical hypotheses were involved in his inductive argu-
ment for his law of gravitation; or possibly he may have be-
come increasingly concerned to create the impression that that
was the case.
It is I suppose possible to interpret Newton’s comments on
the first three of his four rules of reasoning as mere rhetorical
flourishes, signifying nothing very much. Doubtless that is how
they came to be interpreted in subsequent decades and centuries.
My own view is that we should give Newton the credit of
meaning what he said, and he did, in the first edition of the
Principia at least, clearly state that his first three rules of rea-
soning make metaphysical assumptions about the nature of the
universe. This means, of course, that what Newton says here is
inconsistent with what he claims in the General Scholium (an
addition to a later edition) that no hypotheses, metaphysical or
physical, were invoked in his inductive derivation of the law of
gravitation from the phenomena.
Conclusion
There are two conclusions.
First, Newton was wrong when he claimed to have derived
his law of gravitation from the phenomena by induction without
metaphysical hypotheses. On the contrary, in employing his
rules of reasoning during the course of his inductive derivation,
he thereby did adopt metaphysical hypotheses about the nature
of the universe, as he himself in effect acknowledges in his
comments the first three of these four rules.
Second, my long-standing argument is correct. No concep-
tion of science, and of scientific method, is tenable which de-
nies, or fails to acknowledge, that persistent preference for
(more or less) unified theories in physics even when endlessly
many empirically more successful disunified rivals are avail-
able means that physics adopts a permanent metaphysical hy-
pothesis about the nature of the universe: it is such that all se-
riously disunified theories are false. Once this point is acknow-
ledged it becomes clear that we need to adopt the aim-oriented
empiricist conception of science which displays metaphysical
hypotheses of physics in the form of a hierarchy, and thereby
maximizes our capacity to develop and select those hypotheses
best able to promote scientific progress.
REFERENCES
Duhem, P. (1962). The aim and structure of physical theory. New York:
Atheneum.
Harper, W. L. (2011). Isaac Newton’s scientific method. Oxford: Ox-
ford University Press.
Hume, D. (1959). A treatise of human nature. Book 1. London: Every-
man.
Koyré, A. (1965). Newtonian studies. London: Chapman and Hall.
Maxwell, N. (1974). The rationality of scientific discovery. Philosophy
of Science, 41, 123-153, 247-295.
http://dx.doi.org/10.1086/288579
Maxwell, N. (1993). Induction and scientific realism. British Journal
for the Philosophy of Science, 44, 61-79, 81-101, 275-305.
http://dx.doi.org/10.1093/bjps/44.1.61
Maxwell, N. (1998). The comprehensibility of the universe. Oxford:
Oxford University Press.
Maxwell, N. (2000). A new conception of science. Physics World, 13,
17-18.
Maxwell, N. (2002). The need for a revolution in the philosophy of
science. Journal for Genera l Philosophy of Science, 33, 381-408.
http://dx.doi.org/10.1023/A:1022480009733
Maxwell, N. (2004). Is science neurotic? London: Imperial College
Press.
Maxwell, N. (2005). Popper, Kuhn, Lakatos and aim-oriented empiri-
cism. Philosophia, 32, 181-239.
Maxwell, N. (2007). From knowledge to wisdom. London: Pentire
Press.
Maxwell, N. (2011). A priori conjectural knowledge in physics. In M.
Shaffer, & M. Veber (Eds.), What place for the a priori (pp.
211-240)? Chicago: Open Court.
Maxwell, N. (2013). Has science established that the universe is physic-
cally comprehensible? In A. Travena, & B. Soen (Eds.), Recent ad-
vances in cosmology. New York: Nova Publishers Inc.
Newton, I. (1962). Principia, A. Motte’s translation revised by F. Ca-
jori. Berkeley: University of California Press.
Popper, K. R. (1959). The logic of scientific discovery. London: Hut-
chinson.
Popper, K. R. (1963). Conjectures and refutations. London: Routledge
and Kegan Paul.
Popper, K. R. (1972). Objective knowledge. London: Oxford University
Press.
27I am grateful to Harper’s magnificent and detailed book on Newton’s
scientific method for this point: see Harper (2011: p. 362).