Optics and Photonics Journal, 2011, 1, 5-10
doi:10.4236/opj.2011.11002 Published Online March 2011 (http://www.SciRP.org/journal/opj)
The Magnetic Field Effects on Radially Symmetric
Core-Shell-Shell Structure
Hamidreza Simchi1,2, Mahdi Smaeilzadeh2, Mehdi H. Saani1
1Semiconductor Component Industry (SCI), P.O.Box:19575-199, Teh ran, Iran
2Iran University of Science and Technology University, Tehran, Iran
Received February 14, 2011; rev i se d M ar ch 1, 2011; accepted March 9, 2011
Abstract
In this paper, we modeled a core/shell/shell structure with cylindrical Schrodinger-Poisson coupled equation
when a magnetic field is (and is not) applied along its axis. We showed the electron density is peaked near
the outer surface of the channel when the magnetic field is applied. Therefore one may make a nano-device
which its electrons move only on its outer surface. Also we applied a gate voltage to the device and showed a
higher threshold voltage (to turn on the device) is necessary when a magnetic field is applied. This is because
of the increase in the lowest energy level similar to the size quantization. i.e a device with longer channel
looks like a device with shorter channel if it is placed in a magnetic field parallel to its axis.
Keywords: Naowire, Core-Shell-Shell Structure, Self-Consistent Calculation, Quantum Capacitance
1. Introduction
Semiconductor electronic devices including field-effect
transistors (FETs), bipolar transistors, modulation-doped
high-mobility FETs, light emitting diodes (LEDs) and
quantum cascade lasers have revolutionized science and
technology since the invention of the transistors. The
operating principles and performance of these devices
are intimately related to functional interface and/or hete-
rostructures within the devices. These interfaces include
dielectric-semiconductor junctions, semiconductor hete-
rojunctions, p-n homojunctions and metal-semiconductor
junctions. Exquisite control over the composition and
perfection of interfaces is required for the successful
fabrication of high performance planar devices, and is
expected to be equally important in nanoscale devices
given the inherently large surface area to volume ratios.
Among different type of nanostructures semiconductor
nanowires are defined as free-standing semiconductor
structures with diameters of a few to tens of nanometers
with lengths of tens of microns formed by additive, syn-
thetic means rather than subtractive methods such as
lithography and etching. For example, in vapor-liquid-
solid (VLS) synthetic process, metal nanoclusters are
heated above the eutectic temperature for the metal-
semiconductor system of choice in the presence of a va-
por-phase source of the semiconductor, e.g. silane (SiH4)
in the case of silicon. Adsorption of the vapor phase
reactant on the metal catalyst leads to the formation of a
liquid metal-semiconductor alloy (eutectic) at the surface
that eventually consumes the entire catalyst particle.
Continued adsorption of the semiconductor results in
super saturation of the liquid alloy, leading to nucleation
of solid semiconductor and returning the system closer to
an equilibrium in which the solid semiconductor surface
is in contact with the metal-semiconductor liquid. The
solid-liquid interface thus formed is the growth interface,
as the semiconductor in solution condenses here to form
the solid nanowire. Continuous vapor delivery provides
the driving force for diffusion of the semiconductor from
the liquid-catalyst particle surface to the growth interface.
There are two basic heterostructures: axial heterostruc-
tures, in which the heterointerface is perpendicular to the
wire axis, and radial heterostructures, in which the hete-
rointerface is parallel to the wire axis. Lauhon et al. [1]
demonstrated a general method for controlled radial he-
terostructure growth that can be applied to produce o
variety of core-shell materials. Goldberger et al. [2]
demonstrated the formation of GaNAlGaN radial hetero-
structures which might be very useful in optical applica-
tions. Fang Qian et al. [3,4] demonstrated well-defined
doped core/shell/shell (CSS) (n-GaN/ InGaN/p-GaN) and
core/multishell (n-GaN/InGaN/GaN/p- AlGaN/p-GaN) na-
no- wire radial heterostructures which were grown by

H. SIMCHI ET AL.
6
metal-organic chemical vapor deposition (MOCVD).
Nanowires consisting of a p-type Si core and n-type CdS
shell were synthesized, and were used for the fabrication
of nanoLEDs by Oliver Hayden [5] and interface and
defect structures of Zn-ZnO core-shell nanobelts have
been investigated using high-resolution transmission
electron microscopy by Ding et al. [6]. It was shown the
band gap energy of CdSe particles to increase slightly
with the application of a ZnSe shell [7]. Theoretically a
self-con- sistent numerical simulation of
n-Gan/InGaN/AlGaN/n- GaN/MQW/p-GaN was done by
Piprek et al. [8]. A numerical Schrodinger-Poisson solver
for radially symmetric nanowire core-shell structures
was introduced by Lingquan Wang et al. [9]. The strain
distribution and strain induced polarization effect inside
the multiple quantum wells was added to self-consistent
Poisson, drift-diffusion, and Schrodinger solver to study
the spectrum shift and spectrum broadening effect of
micro-photoluminescence from the embedded
GaN/InGaN multi-quantum wells [10].
In this paper, we modeled a core/shell/shell structure
with cylindrical Schrodinger-Poisson coupled equation
when a magnetic field is (and is not) applied along its axis.
We showed the electron density is peaked near the outer
surface of the channel when the magnetic field is applied.
Therefore one may make a nano-device which its electrons
move only on its outer surface. Also we applied a gate vol-
tage to the device and showed a higher threshold voltage
(to turn on the device) is necessary when a magnetic field
is applied. This is because of the increase in the lowest
energy level similar to the size quantization. i.e a device
with longer channel looks like a device with shorter chan-
nel if it is placed in a magnetic field parallel to its axis.
2. Theory
In a magnetic field, the three dimensional Schrodinger
equation becomes

10
2
hh
eAeAU E
mi i


 
 


 
(1)
Where
A

is vector potential. We can rewrite it as


2
2
2
2
22
0
2
heh eh
AA
mmi mi
eA UE
m


 
(2)
If the magnetic field has only component along z-axis,
the vector potential will have the following component in
cylindrical coordinate
02
z
B
AAand A


 (3)
Therefore 0A



(column gauge) and if


iv
Re

  then
2 22222
22
1
228
hR RvehBveB
RRR
mmm


 

 
 




(4)
By changing the variable 1/2 R



 we find
2 2222
2
22
1
24 28
hd ehBveB
v
mmm d
 





 
 


(5)
The Poisson equation is:



2
0
0
rq
Unrn
  

 (6)
which r

is the relative permittivity. Of course it should
be solved self-consistently with Schrodinger equation. Also
it can be written in cylindrical coordinate as

2
2
2
0
1
r
n
dd
d
d

 




 



(7)
The density matrix at equilibrium can be written as the
Fermi function of the Hamiltonian matrix as below [11]:

0
DensityMatrixf HI

 (8)
Which H is Hamiltonian, μ is Fermi energy and I is the
identity matrix of same size as H. It can be shown; the
charge density is given by diagonal elements of density
matrix [11]:


,n DensityMatrix



 
 



 (9)
3. Finite Difference Method
We considered the device with structure as core (5 nm)-
shell (10 nm)-shell(5) in rho-direction and the dimension
in z-direction are enough large. The total dimension of
device is 20 nm. We divided the 20 nm length to 200
pieces and therefore core consists 50 pieces, first shell
consists 100 pieces and second shell consists 50 pieces.
The length of each piece is 0.1 nm. The gate voltage
swept at range (-0.25 to 0.25) volt, and kT is equal to
0.025 volt. Also we assumed the bottom of conduction
band, Ec, is equal to zero in first shell and three electron
volts in core and second shell. The electrochemical po-
tential, μ, is equal to Ec.
The equation five can be written as
2222 22
2
0
22 22
22
0101
2
822
44
nn nn
nn
nnnnnn
eBehBvhv tR
mmm
hh
tRtRR
ma ma
 








  


(10)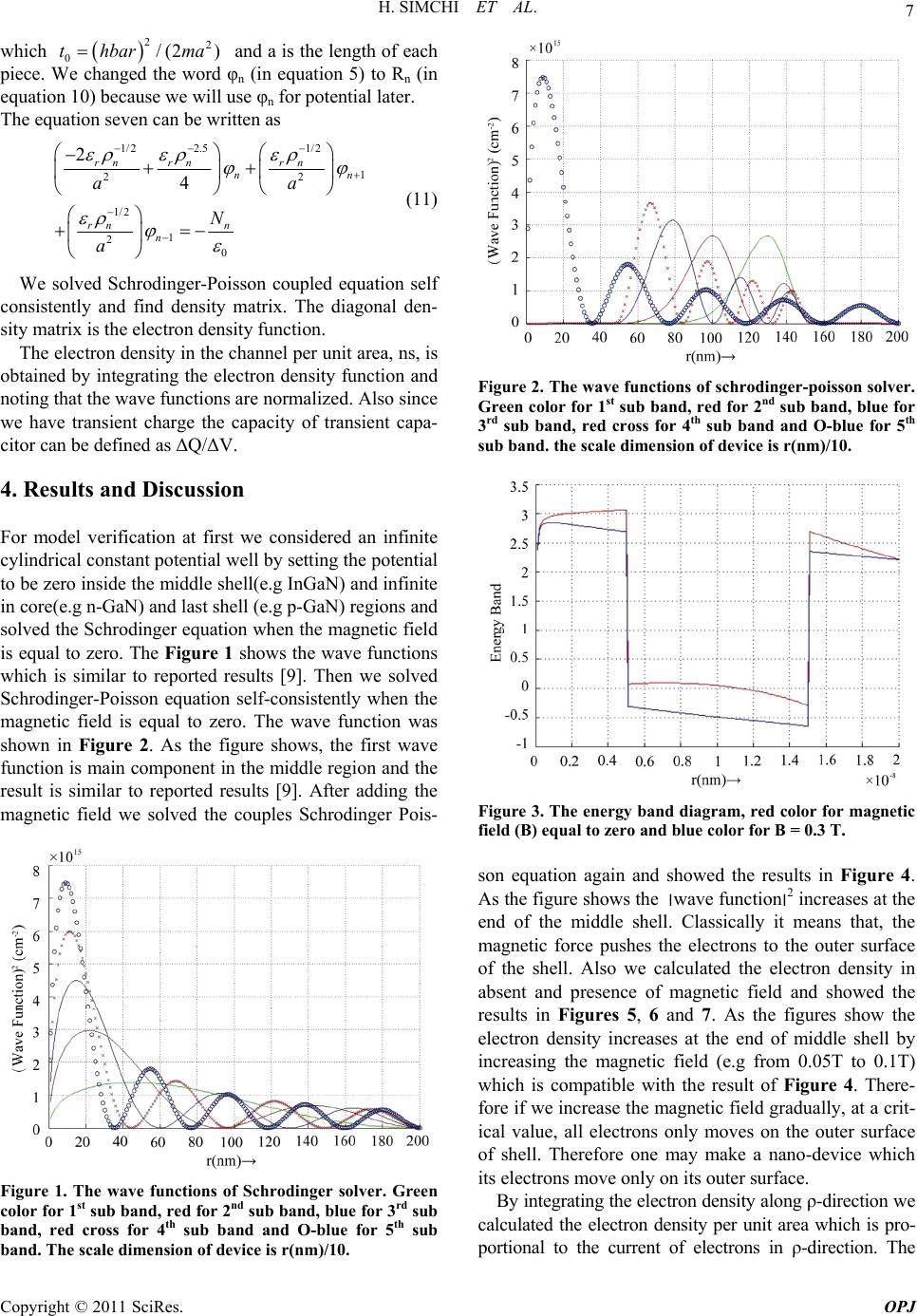

H. SIMCHI ET AL.
7
which

22
0/(2 )thbar ma and a is the length of each
piece. We changed the word φn (in equation 5) to Rn (in
equation 10) because we will use φn for potential later.
The equation seven can be written as
1/22.51/2
1
22
1/2
1
2
0
2
4
rnrnrn
nn
rn n
n
aa
N
a
 


 
 











(11)
We solved Schrodinger-Poisson coupled equation self
consistently and find density matrix. The diagonal den-
sity matrix is the electron density function.
The electron density in the channel per unit area, ns, is
obtained by integrating the electron density function and
noting that the wave functions are normalized. Also since
we have transient charge the capacity of transient capa-
citor can be defined as ΔQ/ΔV.
4. Results and Discussion
For model verification at first we considered an infinite
cylindrical constant potential well by setting the potential
to be zero inside the middle shell(e.g InGaN) and infinite
in core(e.g n-GaN) and last shell (e.g p-GaN) regions and
solved the Schrodinger equation when the magnetic field
is equal to zero. The Figure 1 shows the wave functions
which is similar to reported results [9]. Then we solved
Schrodinger-Poisson equation self-consistently when the
magnetic field is equal to zero. The wave function was
shown in Figure 2. As the figure shows, the first wave
function is main component in the middle region and the
result is similar to reported results [9]. After adding the
magnetic field we solved the couples Schrodinger Pois-
Figure 1. The wave functions of Schrodinger solver. Green
color for 1st sub band, r ed for 2nd sub band, blue for 3rd sub
band, red cross for 4th sub band and O-blue for 5th sub
band. The scale dimension of device is r(nm)/10.
Figure 2. The wave functions of schrodinger-poisson solver.
Green col or for 1st sub band, red for 2nd sub band, blue for
3rd sub band, red cross for 4th sub band and O-blue for 5th
sub band. the scale dimension of device is r(nm)/10.
Figure 3. The energy band diagram, red color for magnetic
field (B) equal to zero and blue color for B = 0.3 T.
son equation again and showed the results in Figure 4.
As the figure shows the ׀wave function׀2 increases at the
end of the middle shell. Classically it means that, the
magnetic force pushes the electrons to the outer surface
of the shell. Also we calculated the electron density in
absent and presence of magnetic field and showed the
results in Figures 5, 6 and 7. As the figures show the
electron density increases at the end of middle shell by
increasing the magnetic field (e.g from 0.05T to 0.1T)
which is compatible with the result of Figure 4. There-
fore if we increase the magnetic field gradually, at a crit-
ical value, all electrons only moves on the outer surface
of shell. Therefore one may make a nano-device which
its electrons move only on its outer surface.
By integrating the electron density along ρ-direction we
calculated the electron density per unit area which is pro-
portional to the current of electrons in ρ-direction. The

H. SIMCHI ET AL.
8
Figure 4. Wave function of Schrodinger-Poisson solver
when magnetic field (B) is equal to 0.3T. Green color for 1st
sub band, red for 2nd sub band, blue for 3rd sub band, red
cross for 4th subband and O-blue for 5th sub band. The scale
dimension of device is r(nm)/10.
Figure 5. The electron density (n) per cm3, when the mag-
netic field is equal to zero.
Figure 6. The electron density (n) per cm3, when the mag-
netic field is equal to 0.05 T.
Figure 7. The electron density (n) per cm3, when the mag-
netic field is equal to 0.1 T.
Figure 8. The electron density per unit area (ns) when the
magnetic field if equal to zero.
result is shown in Figures 8, 9 and 10. As Figures 3 and
14 show, by applying the magnetic field, the energy bang
diagram changed and an increase in the lowest energy
level was seen. Therefore it is expected, a higher threshold
voltage (to turn on the device) is necessary when a mag-
netic field is applied. Also since the transient capacitance
is proportional to ΔQ/ΔV, we calculated the capacitance
and showed the results in Figures 11, 12 and 13. The re-
sults is similar to reported results [9].
5. Conclusion
We considered a core/shell/shell (e.g n-GaN/InGaN/
p-GaN) structure and solved the Schrodinger-Poisson
coupled equation self-consistently in cylindrical coordi-
nate when a magnetic field is (and is not) applied along
its axis (i.e z-axis). When the magnetic field is applied
the electron density increases at the end of middle shell.

H. SIMCHI ET AL.
9
Figure 9. The electron density per unit area (ns) when the
magnetic field if equal to 0.05 T.
Figure 10. The electron density per unit area (ns) when the
magnetic field if equal to 0.1 T.
Figure 11. The capacitance via gate voltage, when the mag-
netic field is equal to zero.
Figure 12. The capacitance via gate voltage, when the mag-
netic field is equal to 0.05 T.
Figure 13. The capacitance via gate voltage when the mag-
netic field is equal to 0.1 T.
Figure 14. The eigenvalue via eigennumbers when the
magnetic field is equal to zero (red color), 0.1 T (green color)
and 0.3 T (blue color).

H. SIMCHI ET AL.
10
Therefore if we increase the magnetic field gradually, at
a critical value, all electrons only moves on the outer
surface of shell and one may make a nano-device which
its electrons move only on its outer surface.
Also it was shown the energy bang diagram changed
and an increase in the lowest energy level was seen the
magnetic field is applied. Therefore it is expected, a higher
threshold voltage (to turn on the device) is necessary when
a magnetic field is applied. The transient capacitance
which is proportional to ΔQ/ΔV, was calculated.
6. References
[1] L. J. Lauhon, M. S. Gudiksen, D. Wang and C. M. Lieber,
“Epitaxial Core–Shell and Core–Multishell Nanowire
Heterostructures,” Nature, Vol. 420, No. 6911, 2002, pp.
57-61. doi:10.1038/nature01141
[2] J. Goldberger et al. “Single-Crystal Gallium Nitride Na-
notubes,” Nature, Vol. 422, No. 6932, 2003, pp. 599-602.
doi:10.1038/nature01551
[3] F. Qian, Y. Li, S. Gradecak, D. Wang, C. J. Barrelet and
C. M. Lieber , “Gallium Nitride-Based Nanowire Radial
Heterostructures for Nanophotonics,” Nano letters, Vol. 4,
No. 10, 2004, pp. 1975-1979. doi:10.1021/nl0487774
[4] F. Qian et al, “Core/Multishell Nanowire Heterostruc-
tures as Multicolor, High-Efficiency Light-Emitting Dio-
des,” Nano letters, Vol. 5, No. 11, 2005, pp. 2287-2291.
doi:10.1021/nl051689e
[5] Oliver Hayden et al, “Core-Shell Naowire Light-Emitting
Diodes,” Advanced Materials, Vol. 17, No. 6, 2005,
pp.701-704. doi:10.1002/adma.200401235
[6] Y. Dind et al, “Interface and Defect Structure of Zn-ZnO
Core-Shell Heteronanobelts,” Journal of Applied Physics,
Vol. 95, No. 1, 2004, p. 306.
[7] T. Mokari and U. Banin, “Synthesis and properties of
CdSe/ZnS Rod/Shell Nanocrystals,” Chemistry of Mate-
rials, Vol. 15, No. 20, 2003, pp. 3955-3960.
[8] Joachim Piprek et al, “Simulation and Optimization of
420 nm InGaN/GaN laser Diodes,” Proceedings of SPIE,
Vol. 3944, 2000, p. 28.
[9] L. Q. Wang et al, “A Numerical Schrodinger-Poisson
Solver for Radially Symmetric Core-Shell Structures,”
Solid-State Electronics, Vol. 50, No. 11-12, 2006, pp.
1732-1739.
doi:10.1016/j.sse.2006.09.013
[10] Y. R. Wu, P. C. Yu, C. H. Chiu, C. Y. Chang and H. C.
Kuo, “Analysis of Strain Relaxation and Emission Spec-
trum of A Free-Standing GaN-based Nanopillar,” Pro-
ceedings Of SPIE, Vol. 7058, 2008, pp. 7058G-7058G-10.
doi:10.1117/12.800658
[11] F. Kootstra, P. L. de Boeij, H. Aissa and J. G. Snijders,
“Relativistic Effects on the Optical Response of InSb by
Time-Dependent Density-Functional Theory,” Journal of
Chemical Physics, Vol. 114, No. 4, 2001, pp. 1860-1865.
doi:10.1063/1.1334615