Creative Education
2014. Vol.5, No.1, 18-30
Published Online January 2014 in SciRes (http://www.scirp.org/journal/ce) http://dx.doi.org/10.4236/ce.2014.51006
18
The Effect of Activity-Based Teaching on Remedying the
Probability-Related Misconceptions: A Cross-Age Comparison
Ramazan Gürbüz1, Emrullah E rdem1, Selçuk Fırat2
1Department of Elementary Mathematics Education, Faculty of Education, Adıyaman University, Adıyaman, Turkey
2Departme nt of Computer Education and Instructional Technology, Faculty of Education,
Adıyaman University, Adıyaman, Turkey
Received November 14th, 2013; revised December 14th, 2013; accepted December 21st, 2013
Copyright © 2014 Ramazan Gürbüz et al. This is an open access articl e d istrib uted u nd er the C reative Commons
Attribution License, which pe rmits unrestricted use, distrib ution, and reprodu ction in any medium, provided the
original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights ©
2014 are reserved for SCIRP and the o wner of the intellectual property Ra mazan Gürbüz et al. All Copyright ©
2014 are guarded by law and by SCIRP as a guardian.
The aim of this paper is to compare the effect of activity-based teaching on remedying probability-related
misconceptions of students at different grades. Thus, a cross-sectional/age study was conducted with a to-
tal of 74 students in 6th-8th grades. Experimental instructions were given to all the groups three times/
week, 40 min/session, for 2 weeks. Students’ progress was examined by pre-test and post-test mea-
surements. The results of the analysis showed that, as a result of the intervention, all graders’ post-test
scores regarding all the concepts (PC: Probability Comparison, E: Equiprobability and R: Representa-
tiveness) showed a significant increase when compared to pre-test scores. It was found out that this
increase did not create a significant difference based on age in PC concept, but that in 8th grade students,
it showed a significant difference in E and R concepts compared to 6th graders. On the other hand, it was
also assessed that the increases observed between 7th and 8th graders with regard to E and R concepts
were not significant. In summary, the implemented intervention can be suggested to have different effects
depending on age and the concept.
Keywords: Activity-Based Teaching; Misconception; Probability; Cross-Age
Introduction
The term “probability learning” is associated with a specific
experimental paradigm within which a person is presented with
a succession of trials on each of which one of two outcomes is
possible and, on each trial, is required to predict which will
happen before showing the outcome (Greer, 2001). Probability
starts at early ages (3 - 5 ages) by comparing two events
quantitatively, and at these ages children are unlikely to calcu-
late the probability of an event. However, they may also reflect
on some events and make some unintentional predictions, such
as “highly probable” or “hardly probable”, “or not equally
probable”. Fischbein (1975) suggested that “when, without
special instructions, the probabilities of the responses approxi-
mate the probabilities of the events, it is possible to assume that
the subject possesses a particular intuition of chance and pro-
bability”. Children, as they grow older, tend to carry out evalu-
ations based on more scientific and numerical calculations, by
putting aside intutional evaluations in calculating and compar-
ing the probability of events. It is believed that during the trans-
formation of these evaluations, strategies employed in teaching
probability concepts are important. Activity-based strategies
must be used, especially during phases when they first confront
probability concepts in formal education. In this sense, Shau-
ghnessy (1977) emphasizes that employing activity-based
teaching is important in providing meaningful learning and in
remedying the students’ misconceptions of probability.
Misconceptions and Probability
One of the most significant factors impeding the comprehen-
sion of a subject is misconception. Misconception is defined as
perceptions or conceptions which are far from the meaning
agreed upon by the experts (Zembat, 2008) or as the
perceptions that are diverging from the view of experts in a
field or subject (Hammer, 1996). For the past 30 years or so,
scholars have studied students’ misconceptions regarding
mathematics. Studies have shown that students’ conceptions of
scientific issues are often not in line with accepted scientific
thinking; that is, they have misconceptions regarding various
notions. Fast (2001), Gürbüz (2007) and Shaughnessy (1977)
suggested that some misconceptions in probability stem from
the nature of the subject or the pupils’ prior theoretical pro-
bability knowledge. Hammer (1996) pointed out that miscon-
ceptions affected students’ perceptions and understandings. Mis-
conceptions make it difficult to understand the subject of prob-
ability. Indeed, many studies were conducted about the mis-
conceptions in teaching mathematics in general, and specifical-
ly in the subject of probability (Barnes, 1998; Batanero & Ser-
rano, 1999; Bezzina, 2004; Dooren, Bock, Depaepe, Janssens,
& Verschaffel, 2003; Fast, 1997, 2001; Fischbein, Nello, &
Marino, 1991; Fischbein & Schnarch, 1997; Garfield &
Ahlgren, 1988; Kahneman & Tversky, 1972; Lecoutre, 1992;

R. GÜRBÜZ ET AL.
19
Mevarech, 1983; Morsanyi, Primi, Chiesi, & Handley, 2009;
Polaki, 2002; Shaughnessy, 1977).
Some Types of Misconceptions
Representativeness Heuristic
When people make guesses about the outcomes of an expe-
riment, they decide about the representativeness of these out-
comes by examining them in certain ways. For example, when
people are asked about the set of outcomes that can be obtained
in an experiment of rolling a die several times successively,
they’re inclined to think that the chances of heads and tails are
equal and the distribution is random (Amir & Williams, 1999;
Shaughnessy, 1977). Similarly, Tversky and Kahneman (2003)
states that “after observing a long run of red on the roulette
wheel, most people erroneously believe that black is now due,
presumably because the occurrence of black will result in a
more representative sequence than the occurrence of an
additional red” (p. 207). They also claim that people expect
that a sequence of events generated by a random process will
represent the essential characteristics of that process even when
the sequence is short. In considering tosses of a coin, for
example, people regard the sequence HTHTTH (H: Head; T:
Tail) to be more likely than the sequence HHHTTT, which does
not appear random, and also HHHTTT more likely than the
sequence HHHHTH, which does not represent the fairness of
the coin.
Positive and Negative Recency
Positive recency misconception is the belief that the outcome
obtained from successive experiments will re-occur in future
trials. Negative recency misconception is, on the other side, the
belief that the outcome obtained from successive experiments
will not occur in future trials. For example, in an experiment of
tossing a coin successively five times and obtaining 5 times
heads repeatedly, the belief that the next trial will also result in
a heads is another example for positive recency effect, just as
the belief that the next trial will result in a tails is known as the
negative recency effect.
Equiprobability Bias
This is the belief that the probabilities of the outcomes of an
experiment are equal although, in fact, they are not. Jun (2000)
showed a different approach and put the equiprobability bias in
three categories. These categories are: a) thinking that each n
different probable outcomes have 50% probability b) thinking
that each outcome has a probability of 1/n c) thinking that the
probabilities of n possible outcomes are all equal if they, in fact,
have similar probabilities. For example, a random selection is
made in a farm containing 100 sheep and 250 goats. Thinking
that the probabilities of choosing a sheep or a goat are equal is
an example of Type (a). In another experiment of rolling to-
gether two dice designed as (123 456) and (222 333); thinking
that the sum of possible outcomes would be equal is an exam-
ple of Type (b). In another experiment of randomly selecting a
student from a class of 20 boys and 25 girls, thinking that the
probabilites of the outcome to be a girl or boy to be equal is an
example of Type (c).
Activity-Based Teaching (ABT)
Activities are defined as tools that help in creating links be-
tween mathematical structures, increasing mathematical power,
and constructing mathematical knowledge and visual illustra-
tions of verbal knowledge (Moyer, Bolyard, & Spikell, 2002).
Piaget (1952) claims that activities should be used in teaching
mathematics due to the fact that mentally immature students
cannot understand mathematical concepts. The activities that
are designed to concretize and present the mathematical ex-
pressions clearly help students think creatively and develop
their worlds of imagination (Thompson, 1992). Through activi-
ties, students will have the opportunity to learn in a more flexi-
ble environment, in collaboration with their peers and will be
engaged in active learning. In parallel, Shaw (1999) states that
he agrees with the educators who claim that students should not
be passive when they build the knowledge. Using activities
during the learning process necessitates active participation of
students.
In an activity-based learning process, students move from an
understanding of getting knowledge directly towards reaching
knowledge, discussing to internalize this knowledge and con-
structing new knowledge through this discussion. This argu-
mentation and constructing process helps students learn togeth-
er, express thei r ideas easily, explain and justify their reasoni ng,
and develop mathematical language. Having a learning envi-
ronment where students argue with each other about valid ar-
guments in mathematics could be the core of mathematics
teaching (Sfard et al., 1998). Thus, it can be said that students’
argumentation plays an important role in the occurrence of such
positive effects in the learning process of probability concepts.
Aspinwall and Shaw (2000) state that the activities allow stu-
dents to make productive arguments about the concepts such as
data, chance and fair and help in developing students’ intui-
tions.
This process offers a learning environment where students
construct the knowledge by sharing their ideas with each other.
It can be said that through such a learning environment, stu-
dents correct each other’s mistakes with the help of their friends
and with the help of the instructor. This interaction among stu-
dents shows the importance of activity-based teaching in these
environments. It can also be stated that through argumentation
between instructor-student and student-student, the instructor
had the opportunity to learn about the students’ thinking and
misconceptions. In sum, by presenting a flexible and reliable
learning environment through active participation of students,
activi ty-based teaching creates a practice-based discussion en-
vironment, contributes to students’ math language and reason-
ing skills and helps students overcome misconceptions.
Literature Review Regarding Probability
(Cross-Age Comparison)
Since prehistoric times, people have faced random physical
events, e.g. unpredictable natural events and games of chance,
but the birth of probability theory and its turning into a branch
of mathematics did not occur until the middle of the 17th
century. Probability as a subject started to appear in school
curricula after the 19th century and since then, cognitive psy-
chologists and mathematics educators have examined students’
misconceptions concerning probability in different age groups
(Batanero & Serrano, 1999; Bezzina, 2004; Dooren et al., 2003;
Fast, 2001; Fischbein et al., 1991; Fischbein & Schnarch, 1997;
Garfield, & Ahlgren, 1988; Gürbüz, Birgin, & Çatlıoğlu, 2012;
Kahneman & Tversky, 1972; Konold et al., 1993; Lecoutre,

R. GÜRBÜZ ET AL.
20
1992; Morsanyi et al., 2009; Offenbach, 1964; Pratt, 2000;
Watson & Kelly, 2004; Watson & Moritz, 2002; Weir, 1962).
For example, Weir (1962) did a study to reveal how three dif-
ferent instructional practices based on the same material af-
fected pupils’ learning in age groups 5 - 7 and 9 - 13. As a re-
sult of the analysis, it was determined that: a) younger pupils
preferred tips and encouragement more than older pupils, b)
older pupils changed their initial answers after receiving tips
more than younger pupils, c) different instructional practices
had no effect on pupils’ selection of situations or choices on
which hints were given, d) it was harder in older pupils to
overcome prejudices. So, it was concluded that the pupils’ pre-
judices or prior knowledge played an important role in their
decisions about chance or probability concepts. Offenbach
(1964), who conducted a study in order to determine the effect
of carrot and stick (or reward and punishment) on a total 60
students’ (30 of preschoolers and 30 of 4th graders) guessing
more frequent event, found that the correct guessing ratios of
both preschoolers and 4th-graders in all groups were almost
equal, and the difference was only in their strategies. As the age
increased, students were observed to make rule-based predic-
tions. Fischbein et al. (1991) found out that the more students’
learning level increases, the more the percentage of correct
answers increases. However, it was also found that as learning
level increases, concept mistakes also increase, yet in some it
decreases. Fischbein and Schnarch (1997), who explored the
changes in misconceptions of 5th, 6th, 7th, 9th, and 11th
graders and college students who had not been educated in
probability, reported that an increase in the students’ education
level variably decreased or increased or did not change their
misconceptions about some concepts. Batanero and Serrano
(1999) conducted a study with 277 pupils aged between 14 and
17 in Spain in order to investigate how the meaning given to
the concept of “randomness” by the pupils changed with age. It
was revealed that age was not important in understanding the
concept of “randomness”; it is a hard concept to understand and,
in order to master it well, it is essential to understand many
other probability concepts, such as sample space, probability of
an event, probability comparisons and so on. Watson and Mo-
ritz (2002) conducted a study to investigate the development of
pupils in answering questions regarding the probability of a
single event, compound events and conditional events. As a
result of the evaluations, when the ratio of groups’ correct an-
swers to the questions related to conditional probability was
compared, it was found that the percentage of correct answers
increased with the level of education. However, no correlation
was found between the level of education and the ratio of cor-
rect answers to the questions related to the probability of com-
plex events. Dooren et al. (2003), who compared misconcep-
tions in 10th and 12th graders, implied that there was no
significant difference between the groups despite an increase in
the level of education decreasing their misconceptions. Watson
and Kelly (2004), who used a test based on a spinner divided
into two identical parts (50 - 50) to determine 3rd, 5th, 7th and
9th graders’ understanding of statistical variation in a chance
setting, identified that there was a steady increase in conceptual
development in the whole process at 3rd, 5th, and 9th grades,
but not for 7th grade. Gürbüz et al. (2012), who compared the
probability-related misconceptions of 540 pupils in 5th-8th
grades, found that the percentage of correct answers increased
when the level of education increased, whereas the misconcep-
tions about the concept of compound events I decreased, the
percentage of correct answers decreased and the misconcep-
tions about the concept of compound events II increased. It was
also found that in concepts of probability of an event and
probability comparisons, as the level of education increased,
both the percentage of correct answers and the misconceptions
increased.
Probability concepts are widely used in decision-making
processes related to uncertain situations we encounter in our
daily lives. In spite of this importance, due to several reasons,
probability concepts are not being taught as effectively in Tur-
key as it is in many other countries. The most important reason
that the subject of probability is not taught effectively is the
existence of this subject-related misconception. The reviewed
literature showed that students’ errors or misconceptions varied
depending on age and level of education. This study aims at
comparing and evaluating the effect of activity-based teaching
on remedying the misconceptions of students at different grades
(6, 7, 8) and ages (12 - 14) regarding some concepts (Probabil-
ity Comprasions-PC, Representativeness-R, Equiprobability-E)
in probability subject.
Method
Research Design
To determine students’ conception in relation to their grade
and understanding, cross-age and longitudinal studies are ge-
nerally used. Despite the fact that the cross-age research in-
volves different cohorts of students, it is more applicable than
the longitudinal study when time is limited (Abraham, Wil-
liamson, & Westbrook, 1994). In these types of studies, moni-
tored groups are few but detailed and comprehensive know-
ledge can be obtained. Also, cross-age studies do provide an
opportunity to observe shifts in concept development as a
consequence of students’ maturity, an increase in intellectual
development, and further learning.
Parti cipants
This study was conducted with a total of 74 pupils (aged 12 -
14) studying in a primary school in the Southeastern Region of
Turkey. The students participating in the study generally come-
from low- or middle-level socio-economic classes (based on the
opinions of the school principal and teachers). The school of
study is located in the province center. Table 1 shows the
grades, ages and class sizes of students in the study group.
Procedure
All of the student groups in the sample had previously been
given a formal education in the subject of probability. Before
the teaching intervention, the Misconception Test (MT) was
Table 1.
The distribution of the students in the study group according to grade
and age.
Grade 6th grade 7th grade 8th gra de
Age 12 13 14
Class Size (n) 23 24 27
(%) 31.08 32.43 36.48

R. GÜRBÜZ ET AL.
21
administered to all groups as a pre-test. All groups were en-
couraged to answer all questions. The subject of probability
was instructed in all groups (6, 7 and 8) with the same strategy
(activi ty-based teaching) and by the same instructor. The
implementations were carried out with 3- or 4-student groups.
Thus, more communication and discussion took place. The six
sessions, each lasting 40 minutes, were planned for the instruc-
tions of the concepts. During these sessions, conceptual
questions that were designed to stretch students’ thinking to a
higher level were asked to the students. These included ques-
tions such as “What strategy did you use to obtain you’re an-
swer?”, “Why, or Why not?” After the intervention, the MT was
administered to all groups as a post-test.
Data Collect ion
In order to collect data, students’ answers to pre- and post-
tests related to each concept and the argumentation among the
students in groups were used. Students’ answers to pre- and
post-tests were taken as a basis in order to determine whether
their misconceptions regarding the concepts Probability Com-
parisons (PC), Representativeness (R) and Equiprobability (E)
were remedied or not.
Instrumentation
The MT consisting of 12 questions (sample questions are
presented in Appendix) was a two-tier question that consisted
of a multiple-choice portion and an open-ended response. Some
of the questions were developed by the researchers, and some
of them were developed with the help of related literature
(Baker & Chick, 2007; Fischbein et al., 1991; Kahneman &
Tversky, 1972; Nilsson, 2009; Tatsis, Kafoussi & Skoumpourdi,
2008; Watson & Kelly, 2004). This test measures students’
conceptions of three principal concepts, each of which involved
4 questions. The validity of the test was confirmed by two
mathematics teachers and two mathematics educators. Further-
more, the pilot test was performed with 120 6th, 7th and 8th
graders who did not participate in the real study. The admini-
stration of the pilot study took one class-hour (40 minutes). The
pilot study revealed that questions on probability subject were
understandable and clear for all grade levels. In this study, the
Kuder-Richardson formula 20 (KR-20) reliability coefficient of
the instrument was found as 0.85.
Activitie s and Materials
The activities used throughout the process of intervention
were implemented in the same format and with the same strate-
gies at all grade levels. The details of these activities are pre-
sented below:
One of the activities undertaken during the intervention
process was the “Which Spinner?” activity. This activity was
carried out using spinners A and B (see Figure 1). Spinner A
has 4 identical red parts and 2 identical green parts. Among
these six identical parts, two parts were numbered as 2 and four
parts were numbered as 5. On the other hand, Spinner B has 2
identical red parts and 4 identical green parts. These identical
parts are numbered as 1, 2, 3, 4, 5, and 6 respectively. Before
and after the spinners were turned, the teacher asked the stu-
dents questions such as, “Which of the spinners is more likely to
stop in a red area?”, “What is the relationship between the
probabilities of spinner A to stop in a red area and spinner B to
stop in a green area?, Why?”, “Are the probabilities of both
spinners A and B to stop in the area numbered as 5, equal?”
The teacher tried to obtain the full participation of the students.
The students turned the spinners with a variety of designs as
shown in Figure 2 many times, and the teacher helped to
deepen the discussion environment by directing them in similar
questions as shown above.
Another activity was the “Which Number” activity. In this
activity, a material which had 16 tip up parts numbered from 1
to 16 respectively and each part had an area of 1 m2 was used as
given in Figure 2. Different amounts and frequency of points
or chocolates were hidden in some places of this material.
Some places were left without any reward. The scores written
on the parts of the material, the number and frequency of choc-
olates and blank parts on the materials were written on the
board, but these amounts were changed at the beginning of each
activity. The groups were asked different questions about these
materials. For example “A randomly opened box will be more
likely to be full or empty?”, “In a randomly opened box, will the
content more likely be a chocolate, or a score?”, “What is the
Figure 1.
Materials and reflections from the teaching process.
Figure 2.
Materials and reflections from the teaching process.

R. GÜRBÜZ ET AL.
22
probability of a randomly opened box to be empty?” In this pro-
cess, a group receives whatever comes out from the randomly
opened box, either a chocolate, or a score. However, if an emp-
ty box is chosen, then this group is left out from the activity.
Another activity used in this process is the activity of “Roll-
ing Dice”. For this activity, the researchers brought the class
several dice designed in different forms (for example; 123 456,
111 444, 44 6666, or 123 455). The instructor first distributed
these dice to the students and wanted them to do many experi-
ments (50, 70, 100), to note the results of these experiments and
to discuss these records. Then, the teacher transferred the
records of all groups onto the board and enabled them to see the
results of their experiments. The groups were asked to discuss
these results and their ratios among themselves and by asking
questions such as, “Compare the ratios of the results obtained
from the 123 456 die with those obtained from the 123 455 die”,
“Compare the ratios of the results obtained from the 111 444
die with those obtained from the 44 6666 die.”
The last activity was “Deal or No Deal?” activi ty. After a
short question-answer episode, the content of the activity was
briefly explained to the students. If we want to explain the
content of the activity here briefly, there are 10 boxes labeled
with numbers between (1 - 10), as in Figure 3, and different
amounts of money (1 TL, 5 TL, 10 TL, 10 TL, 20 TL, 20 TL,
20 TL, 50 TL, 100 TL) were put in these boxes. The amounts of
money and their frequencies were altered at the beginning of
every game. These amounts of money were put in an ascending
order on the board in a way all students can see, and the fre-
quency of each amount was indicated on the side. When the im-
plementation process initiated, students competed to participate.
Although all the class participated in the process, 10 students
competed on the board beside the boxes, and one student took
part as the single contestant. While all boxes were closed, the
contestant picked the number of the box he wanted to be
opened and then wanted the help of his/her friends on predic-
ting the amount of money inside the box. His/her friends tried
to uncover the contestant’s thoughts by asking questions such
as, “Why thi s bo x? ” After obtaining the thoughts of all the class,
the contestant decided that either the box would be opened, or it
Figure 3.
Materials and reflections from the teaching process.
would be changed. The teacher organizing this process as a
conductor asked students several questions before each box was
opened, for example, “Which amount of TL has the highest pro-
bability as an outcome?”, “Which amount of TL has the lowest
probability as an outcome?”, “What’s the probability of picking
100 TL”, “Which amounts of TL have the same probability?”,
“Do you think the skills of the player have anything to do with
winning the game? Why?” A similar process went on until all
boxes had been opened, and from time to time, by considering
the amounts of money in the unopened boxes, different offers
were made to the contestant. If the contestant accepted the offer,
the game ended, but if not, the game continued until all boxes
were opened. The contestants beside the boxes and the single
contestant were changed every time and all the class was given
the opportunity to participate in the activity.
Data Analysis
In analyzing the data, students’ answers were classified in
rega rd to the le vels in Table 2. Since two external mathematics
educators who had experience in analyzing qualitative data
initially categorized the data separately, they discussed the
consistency of the categorization. There was high agreement,
approximately 90%, in most of the categorization. All dis-
agreements were resolved by negotiation. The assessment test
consisted of two phases (1st phase multiple choice, 2nd phase
open-ended), and, therefore, the assessment criteria also con-
sisted of two phases. In this paper, the following symbolism is
used for indicating the grade to which the quoted subjects
belong: G6 means Grade 6, just as G followed by 7 or 8 in-
dicates the respective grade.
Each group’s total score was calculated and inputted into
SPSS, and statistical comparisons were made in terms of the
misconception level of groups. Two-way repeated measures
ANOVA was employed to compare pre-test scores with post-
test scores in each concept in MT.
Results and Discu ssion
Results of pre-test and post-test of the groups regarding MT
were presented in Table 3 and Figure 4. One-way ANOVA
was carried out in comparing the pre- and post-test results of
the groups.
The one-way ANOVA test was used to compare groups’
scores regarding MT in pretest. As shown i n Table 4 , a signifi-
cant difference was found between groups’ pre-test scores rela-
ted to PC [F (2 - 68) = 8.693, p < 0.01], and it was revealed that
this difference was (Mean difference = 0.42572, p < 0.01) age;
Figure 4.
Pre-test and Post-test scores of the groups on PC, E, and R concepts.
0,00
0,50
1,00
1,50
2,00
2,50
3,00
Pre-test Post-testPre-test Post-testPre-test Post-test
PC E R
6t h Grade
7t h Grade
8t h Grade

R. GÜRBÜZ ET AL.
23
Table 2.
The rubric developed and used for MT and students’ sample responses to them.
Comprehension
Levels Explanation SCORE
Assessment
Criteria 1st
Phase
–2nd Phase Sample Response
Correct
Justification
Answers that
encompass all
aspects of the
valid
justification
3
Correct Answer
Correct
Justification
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
PC 2: In the table above, there are 2 outcomes for Musa to win the game whereas there are 5
outcomes f or Meryem to win the game. Thus, Meryem’s chance to win the game is higher.
E1: When two dice are rolled together, the sums “2” and “12” are obtained one time. For 2 the
outcome i s t o be (1,1), and for 12 the outcome is to be (6,6). So, Choice c (see Table be l ow).
+ 1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
2 Incorrect Answer-Correct
Justification
R1: Choice a is the correct answer. The number of elements in the sample universe of an
experiment is 2. The c hances of heads a nd t ails are equal in the next toss; therefore, the outcome
may be both.
R3: As distributon of outcomes is more random, choic e c is more rea l i s t i c.
Partially
Correct Justifica-
tion
Answers that do
not encompass
all aspects of
the valid justi-
fication
2 Correct Answer -
Partially Correct
Justification
E4: Choice c is the correct answ er. Because t he probabiliti es of stopping at yellow and blue
colors are equal in both cases.
PC 1: Choice b, because there are more green balls in the basket.
1
Incorrect
Answer-Partially
Correct
Justification
R3: The answer is choice a. According to me, the probabi l i ty of each letter on the dice is 1/6,
and therefore the probability of each letter is equal.
PC 4: There are equal numbers of red-coloured par t s i n both spinners. But, in spinner B, all
red-coloured parts are together. Choice b.
Wrong
Justification
Answers that
contain incor-
rect knowle dge
1 Correct Answer-Wrong
Justification
PC 2: Meryem’s chance to win is = 6/9, and Musa’s chance is = 3/9. So, Meryem’s chance is
higher.
E4: Since 3 people s pun Spinner A and 5 spun Spinne r B, choice c is correct.
0 Incorrect Answer-Wrong
Justification
E1: Chances of 2 is = 2/14 and chanc es of 12 is = 12/14 so the sum will more likely be 12.
R1: Choice b, in this toss, tail comes, because all toss before are head.
No Justification
Correct,
incorrect or
blank answer s
with no
justifications
written.
1 Correct Answer–No
Justification …
0 Incorrect Answer–No
Justification …
0 No Answer–No
Justification …
PC: Proba bility Comparisons, R: Repres entative ness, E: Equiprobability.
c) between 8th and 6th graders, while it was (Mean difference =
0.26042, p < 0.05) between 8th and 7th graders. However, no
significant difference was found between groups’ pre-test
scores E [F (2 - 68) = 2.040, p > 0.05] ve R [F (2 - 68) = 0.943,
p >.05]. Therefore, it can be said that all groups had the same
level of misconceptions in E and R concepts prior to the
instructional process. Moreover, when the pretest results of the
groups are compared, it can be seen that the number of
misconceptions changes significantly depending on age related
to the concept PC. It could be noted that: a) there is better
understanding of this concept depending on age; b) students
have to use this concept throughout their growing by teachers

R. GÜRBÜZ ET AL.
24
possess affluent knowledge of this concept; d) an effective
presentation of this concept in all levels was effective in the
creating of such a picture related to PC concept. It could also be
maintained that in E and R concepts, less use of these concepts
in daily life and teachers’ lack of knowledge related to these
concepts played a role.
As can be observed in Figure 4 and Table 3, as a result of
intervention, the number of answers with misconceptions in all
groups related to PC, E and R concepts was lessened.
Table 5 illustrates that intervention created a siginificant
effect in remedying misconceptions related to PC, E and R
concepts in all class levels.
It could be understood from Table 5 that as a result of
intervention, misconceptions related to PC concept in 7th grade
students (Mean = 1.19) were decreased more compared to 6th
grade (Mean = 1.10) and 8th grade students (Mean = 1.08). It is
also shown that this effect was higher in 8th graders (Mean =
1.61) related to E concept compared to 7th (Mean = 1.43) and
Table 3.
Descriptive statistics.
Concept Measure Grade 6 Grade 7 Grade 8
M SD M SD M SD
PC Pre-test 1.03 0.35 10.19 0.34 1.45 0.35
Post-test 2.14 0.31 2.39 0.32 2.54 0.29
Improvement* 1.10 0.52 1.19 0.50 1.08 0.37
E
Pre-test
0.98 0.33 0.85 0.37 0.97 0.32
Post-test 2.03 0.32 2.29 0.29 2.59 0.33
Improvement* 1.04 0.37 1.43 0.46 1.61 0.46
R
Pre-test
0.94 0.41 1.00 0.48 1.06 0.38
Post-test 1.97 0.21 2.44 0.38 2.61 0.44
Improvement* 1.03 0.33 1.44 0.66 1.55 0.62
Table 4.
The comparison of Pre-test scores of groups on MT related with the all concepts using ANOVA.
Measure Sum of Squares df Mean Square F p Difference
PC Between Groups 2.172 2 1.086 8.693 0.000 8th grade > 6th gr ade
Within Groups 8.494 68 0.125 8th grade > 7th grade
Total 10.665 70
E
Between Groups
0.269 2 0.135 1.121 0.332 no significance
Within Groups 8.164 68 0.120
Total 8.433 70
R
Between Groups
0.161 2 0.080 0.436 0.648 no significance
Within Groups 12.526 68 0.184
Total 12.687 70
Table 5.
Groups’ paired t-test results.
Grade Pre-test-Post-test Mean Difference SD t df p
6th grade
PC
1.10870 0.52671 10.095 22 0.000
E 1.04348 0.37426 13.371 22 0.000
R 1.03261 0.33966 14.580 22 0.000
7th grade
PC
1.19792 0.50529 11.614 23 0.000
E 1.43750 0.46186 15.248 23 0.000
R 1.44792 0.66340 10.692 23 0.000
8th grade
PC
1.08333 0.37349 14.210 23 0.000
E 1.61458 0.46026 17.185 23 0.000
R 1.55208 0.62978 12.073 23 0.000

R. GÜRBÜZ ET AL.
25
6th graders (Mean = 1.04), that related to R concept, it was
higher in 8th graders (Mean = 1.55) compared to 7th graders
(Mean = 1.44) and 6th graders (Mean = 1.03). Results of
one-way ANOVA and Tukey HSD test applied to assess if the
intervention had a class-level significant effect in remedying
misconceptions related to PC, E and R concepts are shown
below.
Table 6 shows that the intervention created a significant
difference in terms of remedying groups’ misconeptions related
to all concepts but that this effect was not significant in PC [F
(2 - 68) = 0.368, p > 0.05] concept depending on age but it wa s
significant in E [F (2 - 68) = 10.568, p < 0.01] and R [F (2 - 68)
= 5.505, p < 0.01] concepts depending on age. According to
Tukey HSD results, as shown in Table 7, misconceptions re-
lated to E concept were overcome more significantly by 8th
[mean difference = 0.57111, p < 0.01] and 7th [mean difference
= 0.39402, p < 0.01] graders than 6th graders, but this effect
was not significant in 8th graders compared to 7th [mean
difference = 0.17708, p > 0.05] graders. Similarly, miscon-
ceptions related to R concept were overcome more significantly
by 8th [mean difference = 0.51947, p < 0.01] and 7th [mean
difference = 0.41531, p < 0.01] graders than 6th graders, but
this effect was not significant in 8th graders compared to 7th
[mean difference = 0.10417, p > 0.05] graders. It could be s aid
the fact that in removal of groups’ misconceptions at similar
level in PC concept, students had a certain level of knowledge
related to this concept, and understanding of this concept does
not necessitate much theoretical knowledge were effective. It
could also be stated that in removal of groups’ misconceptions
at different levels in E and R concepts, in addition to students’
age, their knowledge about other probability concepts in
understanding these concepts and the need for deeper logical
reasoning were effective. It is specifically important to say that
in addition to the intervention conducted, age also played a role
in removal of groups’ misconceptions related to E and R
concepts. In other words, it could be inferred that as age level
increases, the intervention led to a greater decrease in mis-
conceptions related to E and R concepts. Gürbüz et al. (2012)
reached similar findings.
When the answers of participants were examined, it was
found that students had different justifications for their right or
wrong answers in pre- and post-test. Since the research group
consists of 74 students in total, all papers in pre-test and post-
test could be examined in detail. However, since it was not pos-
sible to transfer all answers by students to the study, some sam-
ple student answers were given.
For example regarding PC 1, some students were found to
give incorrect answers in pre-test either because of building a
relationship with general chance factor and favourite color
concept or because of concentrating on the location of the balls
in the basket. For example, “We can say nothing unless we
know the favourite colors of the person who choses the balls
(G7)”, “I can’t comment on it because it depends on chance
(G6;G7)”, “Green, because they’re at the bottom and when the
basket is mixed they will be at the top (G6)”. Such approaches
of students who gave wrong or misconcept ional answe rs to ques-
tion PC 1 are in line with the student approaches in the studies
of Gürbüz (2007; 2010), Gürbüz, Çatlıoğlu, Birgin and Erdem
(2010) and Jones et al. (1997). In addition, as a result of the
effect of intervention, more correct answers were observed in
all grade levels. Explanations related to question PC 1 made by
some of the students in post-test are as follows: “Green because
the number of green balls in the basket is the highest (G6;
G7;G8)”, “Choice b, since the number of green balls in the bas-
ket is higher than others, the probability of getting green is the
highest. Numerically, P(G) = 4/9 (G7;G8)”.
It was found that, regarding question PC 2, some of these
students used general chance factor in probability subject, while
another group used the perception that the probabilities will be
the same and a small portion gave illogical justifications in
pre-test. “The families of Musa and Meryem should be checked;
whoever was born in a luckier family will win (G7)”, “Musa
and Meryem have the same chance. Because there’s only one 3
and one 6 on the die (G6;G7;G8)”, “3 + 6 = 9: 2 = 4, 5 bot h ha ve
the same chance to win (G6)”. It should be noted here that, as
students’ ages and level of education increased they tended to
answer the question by relating it to chance factor. Amir and
Williams (1999), Baker and Chick (2007), Batanero and
Serrano (1999), Fischbein et al. (1991), Lecoutre (1992) and
Nilsson (2007) reported similar conclusions in their studies.
Some of the students who gave misconceptional answers also
used some probable outcomes as reported by Amir and
Williams (1999). For example, “Musa is my favourite because
Table 6.
The compar ison of post-test scores of groups on MT related with all concepts using ANOVA.
Variable Sum of Squares df Mean Square F p
PC
Between Groups
0.173 2 0.087 0.388 0.680
Within Groups 15.184 68 0.223
Total 15.357 70
E
Between Groups
3.997 2 1.999 10.568 0.000
Within Groups 12.860 68 0.189
Total 16.857 70
R
Between Groups
3.527 2 1.764 5.505 0.006
Within Groups 21.783 68 0.320
Total 25.310 70

R. GÜRBÜZ ET AL.
26
Table 7.
Tukey HSD results.
Variable (I) grup (J) grup Mean Difference (I-J) Std. Error p
E Improvement
7th grade
6th grade 0.39402* 0.12690 0.008
8th grade
6th grade 0.57111* 0.12690 0.000
7th grade 0.17708 0.12554 0.341
R Improvement
7th grade
6th grade 0.41531* 0.16515 0.038
8th grade
6th grade 0.51947* 0.16515 0.007
7th grade 0.10417 0.16338 0.800
when the outcomes are (1,2) and (2,1), their sum would be three.
On the other hand, in order to obtain six, there’s only (3,3)
(G7)”, “Musa and Meryem have the same chance. Because for
3, (1,2), (2,1) and for 6, (1,5), (5,1) (G7;G8)”. Such miscon-
ceptional answers from students can be argued to stem from
students’ l ack of sufficient knowledge in sample space concept.
In parallel, Baker and Chick (2007), Bezzina (2004), Chernoff
(2009), Fischbein et al. (1991), Gürbüz (2007; 2010), Keren
(1984), Nilsson (2007) and Polaki (2002) showed in their
studies that students’ knowledge about sample space concept
played an important role in their answers to questions related to
probability subject. Moreover, few students gave miscon-
ceptional answers by considering gender factor as reported by
Amir and Williams (1999). For example, “Musa is the favourite.
Becuase, males are more lucky in this kind of chance games”
(G6;G7). In question PC 2, it’s understood that students’ jus-
tifications are effected from their individual learning, ex-
periences, cultures and beliefs. Amir and Williams (1999),
Fischbein et al. (1991), Sharma (2006) and Shaughnessy (1993)
reported similar results in their studies. When students’ an-
swered PC 2 question in the post-test, it could be seen that a
great number of answers that did not make sense were corrected.
For example, “Choice b, because 6 is (G6;G7),”,”Meryem is
more advantegous as the probability of total score to be 6 is
high (G6;G7), “Choice b, because cases where Musa will win
are (1,2) ve (2,1) but cases where Meryem will win are (1,5),
(5,1), (2,4), (4,2) and (3,3). Since Meryem has more cases to
win, she is more advantegous (G7;G8)”.
Many students realized the importance of size in solving
question PC 4, but they gave answers containing misconce-
ptions because they concentrated on only one aspect of size in
the pre-test. For example, some of the students gave answers
such as, “Choice b, because on spinner B the red color covered
more than half of the shape (G6;G7)”, “The probability of
spinner B to stop on a red color is higher because there are
more red areas (G7;G8)”. On the other hand, there were an-
swers to question PC 4 contrary to mathematical logic such as
“We can not decide at what colors the spinners will stop be-
cause we don’t know at what speed they are turned (G6)”,
“When looking at the direction of the arrow, both have a high
chance to stop at red color (G7)”. However, though some mis-
takes made related to PC 4 question in the pre-test were re-
peated by a few students, most students gave correct answers in
the post-test. For example, “Choice B, since red colours are
gathered on spinner B (G6;G7)”, “The probability of stopping
in a red area on both spinners are equal (G6;G7;G8)”, “As the
areas covered by red colour on both spinners are equal, choos-
ing A or B does not change my chance to win. P(A) = P(B) =
6/12 (G6;G7;G8)”.
It was found that, in question E 1, some of the students
couldn’t reason probabilistically, and they couldn’t think or
know that there was no number greater than 6 on the faces of a
traditional die in the pre-test. For example, “12 is more likely
because 12 is greater than 2 (G6;G7)”, “For the sum to be 2, the
dice should be (1,1); for the sum to be 12, the dice should be
(8,4), (6,6), (7,5), (9,3), (10,2), (11,1). Therefore the probability
of 12 is higher (G7;G8)”. Polaki (2002) names this type of
thinking as subjective probabilistic thinking, and, according to
him, the students reflecting at this level can not give logical or
mathematical answers. On the contrary, Bezzina (2004) pointed
out that the students falsely believe that a “six” is the most
difficul t scor e to obt ai n whe n a die is rolled at random. It could
be said that students gave more correct answers to E 1 question
in the post-test. For example, “Choice C, for the sum to be 2,
the dice should be (1,1); for the sum to be 12, the dice should
be (6,6), thus, the probability of the total to be 2 or 12 is
equal(G6;G7;G8)”, “When a die is rolled, in total, the minimum
will be 2 and maximum will be 12 and there is only one case
where each of these total numbers could be gathered (G7;G8),
so choice C is true”.
Students gave answers containing misconceptions to
question E 4 by using their intuitions and informal strategies in
the pre-test. For example, “I would choose spinner B because
more people turn it (G6;G7;G8)”, “3 people are turning spinner
A, 5 people are turning spinner B therefore in order to equalize
the number of people turning each spinner, I would choose
spinner A (G6;G7)”. It could be argued that the students giving
such kinds of justifications have “Outcome Approach” misc on-
ception. Likewise, according to Jun (2000) and Konold (1989),
students who have this kind of misconception make decisions
considering the results of previous outcomes. It is possible to
see that students gave more correct answers in the post-test. For
example, “Since the probability of A spinner to stop on yellow
and of B spinner to stop on blue color are equal, it does not
make a difference (G6;G7;G8)”, “Both the yellow and blue
areas cover half of the circle, that is why, the answer is C
(G6;G7;G8)”, “Choice C, the probability of A spinner to stop
on yellow and of B spinner to stop on blue color is 50 % (G6;
G7;G8)”.
In question R 1, some of the students mostly showed

R. GÜRBÜZ ET AL.
27
misconceptions of positive and negative recency in the pre-test.
For example, “The first four outcomes were heads. So, the fifth
toss would more likely be tails (Negative recency) (G6;G7;
G8)”, “The successive outcomes were heads. So, the next toss
will more likely result in heads (Positive recency) (G6;G7;
G8)”. It is expressed that children’ gender could be guessed
through the same approaches. For instance, Kahneman and
Tversky (1972) stated that for a family with 6 children, it’s
believed that the order of the genders will more likely be
MFFMFM (M:Male; F:Female) instead of MMMMMM or
MMMFFF. It’s possible to find similar results in the study by
Fast (1997). However, students in the post-test learnt first
tosses would not affect later tosses. For example, “The pro-
bability of getting heads and tails are the same because there
are two faces of the coin, being heads and tails (G6;G7;G8)”,
“The outcome in the previous toss does not affect the later one,
thus Choice C. (G6;G7;G8)”, “Since getting heads and tails are
independent events, the probability of getting either one is the
same (G7;G8)”.
In question R 3, only a few students at all levels gave
justification in the pre-test. This concept is hard to understand
and in order to understand it first other concepts (Sample Space,
The Probability of an Event, Probability Comparison) should be
well comprehended. Some students showed the misconception
of representativeness heuristic in this question. For example,
some students stated that “Choice a, because it’s more realistic
that all faces come as an outcome equal times (G6;G7;G8)”,
“All the outcomes have equal probability, so choice a
(G6;G7;G8)”, “Choice c, in which the same order exists, is
more probable (G6;G7)”.Batanero and Serrano (1999),
Shaughnessy (1977) and Gürbüz and Birgin (2012) obtained
results in their studies similar to these. Batanero and Serrano
(1999) found that smaller children dealt more with runs, or
whether heads and tails come out in an order; whereas, older
students focused more on the number of heads and tails.
Though it was possible to see some answers given in the
post-test similar to answers with misconceptions in the pre-test,
it was observed that more correct answers were given in all
grade levels. For example, “Choice b, because when this die is
tossed it is not realistic to get both faces equally (G6;G7; G8)”,
“Since the distribution is more randomly, b is more logical
(G7;G8)”, “As more regular outcomes are gathered succes-
sively c is a more correct anwers (G6;G7;G8)”.
In summary, it can be argued that with the implemented
intervention, all graders’ scores increased and the number of
misconceptions decreased. On the other hand, while there was
not any singnificant relationship between age and remedying
misconceptions in groups related to PC concept, it could
generally be noted that, depending on age, the intervention
helped students remedy more misconceptions in E and R
concepts.
Conclusions and Implications
When the pre-test results are examined, a significant dif-
ference was observed between groups’ misconceptions related
to PC concept, and this difference was found between 8th and
6th graders and 8th and 7th graders. On the other hand, no
significant difference was found among groups related to E and
R concepts. However, as a result of the intervention, all graders’
post-test scores regarding all the concepts showed a significant
increase when compared to pre-test scores. While there was no
any singnificant relationship between age and remedying mis-
conceptions in groups related to PC concept, it could generally
be noted that, depending on age, the intervention helped stu-
dents overcome more misconceptions in E and R concepts. It
was determined that the intervention did not make a significant
difference according to age in remedying misconceptions re-
lated to PC concepts in groups, but that age had a significant ef-
fect on overcoming misconceptions (more in 7th and 8th gra-
ders than 6th graders) in E and R concepts. To summarize, it
can be suggested that the implemented intervention has dif-
ferent effects depending on age and the concept. Activity-based
teaching, which contributes to remedying misconceptions and
provides learning relevant to real life, should be performed in
the subject of mathematics.
The number of justifications related to the concepts in MT
was found to increase with the increase of age when par-
ticipants’ answers were examined. This could be attributed to
the development of mathematical reasoning and language in
addition to age factor. As a matter of fact, in learning pro-
bability concepts, Fischbein et al. (1991), Offenbach (1964),
Watson and Moritz (2002), and Way (2003) emphasized age,
Erdem (2011), Lamprianou and Lamprianou (2003), Memnun
(2008), Offenbach (1965) and Olson (2007) focused on mathe-
matical reasoning, Ford and Kuhs (1991), Gibbs and Orton
(1994), Kazıma (2006) and Tatsis et al. (2008) mentioned the
effect of language development. In this sense, for further re-
search, the relationship between age and language develop-
ment, and between age and mathematical reasoning should be
studied.
Argumentation is an important process both in learning ma-
thematical concepts and in analyzing the nature of activity wi-
thin mathematics classrooms (Sfard et al., 1998). This process
must be consciously made use of in the teaching of concepts
that require a deeper thinking, such as probability concepts. Ac-
tivities used in this study contributed to the discussion process
being more consciously and productively executed. It revealed
that during the process, groups consisting of more aged mem-
bers had more effective discussions. It is believed that the ef-
fective discussion process was effective in the development of
aged groups’ learning of some probability concepts. Because of
this reason, discussion environments must be created in maths
teaching starting from early ages.
REFERENCES
Abraham, M. R., Williamson, V. M., & Westbrook, S. L. (1994). A
cross-age study of the understanding five concepts. Journal of Re-
search in Science Teaching, 31, 147-165.
http://dx.doi.org/10.1002/tea.3660310206
Amir, G., & Willi ams, J. (1999). Cultu ral influences on children’s p ro-
babilistic thinking. Journal of Mathematical Behavior, 18, 85-107.
http://dx.doi.org/10.1016/S0732-3123(99)00018-8
Aspinwall, L., & Shaw, K. L. (2000). Enriching students’ matematical
intuitions with probability games and tree diagrams. Mathematics
Teaching in the Middle School, 6, 214-220.
Baker, M., & Chick, H. L. (2007). Making the most of chance. Austra-
lian Primary Mathematics Classroom, 12, 8-13.
Barnes, M. (1998). Dealing with misconceptions about probability.
Australian Mathematics Teacher, 54, 17-20.
Batanero, C., & Serrano, L. (1999). The meaning of randomness for
secondary school students. Journal for Research in Mathematics Edu-
cation, 30, 558-567. http://dx.doi.org/10.2307/749774
Bezzina F. (2004). Pupils’ Understanding of Probabilistic & Statistics
(14-15+) Difficulties and Insights For Instructio n. Journ al of Ma ltese

R. GÜRBÜZ ET AL.
28
Education Research, 2, 53-67.
Chernoff, E. J. (2009). Sample space partitions: An investigative lens.
Journal of Mathematical Behavi or , 28, 19-29.
http://dx.doi.org/10.1016/j.jmathb.2009.03.002
Dooren, W. V., Bock, D. D ., Depaepe, F., Janssens, D., & Verschaffel,
L. (2003 ). The illusion of lin earity: Expanding the evidence towards
probabilistic reasoning. Educational Studies in Mathematics, 53, 113-
138. http://dx.doi.org/10.1023/A:1025516816886
Erdem, E. (2011). An investigation of the seventh grade students’ ma-
thematical and probabilistic reasoning skills. M.A. Thesis, Adıya-
man: Adıyaman University.
Fast, G. (1997). Using analogies to overcome student teachers’ pro-
bability misconceptions. Journal of Mathematical Behavior, 16, 325-
344. http://dx.doi.org/10.1016/S0732-3123(97)90011-0
Fast, G. (2001). The stability of analogically reconstructed probability
knowledge among secondary mathematics students. Canadian Jour-
nal of Science, Mathematics and Technology Education, 1, 193-210.
http://dx.doi.org/10.1080/14926150109556461
Fischbein, E. (1975). The intuitive sources of probabilistic thinking in
children. Reidel, Dordrecht, The Netherlands.
http://dx.doi.org/10.1007/978-94-010-1858-6
Fischbein, E., & Schnarch, D. (1997). The evolution with age of pro-
babilistic, intuitively based misconceptions. Journal of Research in
Science Teaching, 28, 96-105.
Fischbein, E., Nello, M. S., & Marino, M. S. (1991). Factors affecting
probabilistic judgements in children and adolescents. Educational
Studies in Mathematics, 22, 523-549.
http://dx.doi.org/10.1007/BF00312714
Ford, M. I., & Kuhs , T. (1991). The act of in vestigating: Learning ma-
thematics in the primary grades. Childhood Education, 67, 313-316.
http://dx.doi.org/10.1080/00094056.1991.10520819
Garfield, J., & Ahlgren, A. (1988). Difficulties in Learn ing Basic Con-
cepts in Probability an d Statistics: Imlications for Research. Journal
for Research in Mathematics Education, 19, 44-63.
http://dx.doi.org/10.2307/749110
Gibbs, W., & Orton, J. (1994). Language and mathematics. İn A. Orton,
& G. Wain, (Eds.), Issues in teaching mathematics (pp. 95-116),
London: Cassell.
Greer, B. (2001). Understanding probabilistic thinking: The legacy of
Efrahim Fischbein. Educational Studies in Mathematics, 45, 15-33.
http://dx.doi.org/10.1023/A:1013801623755
Gürbüz, R. (2007). The effects of computer aided instruction on stu-
dents’ conceptual development: A case of probability subject. Eura-
sion Journal of Educational Research, 28, 75-87.
Gürbüz, R., Çatlıoğlu, H., Birgin, O., & Erdem E. (2010). An inves-
tigation of fifth grade students’ conceptual development of probabi-
lity through activity based instruction: A quasi-experimental study.
Educational Sciences: Theory & Practice, 10, 1021-1069.
Gürbüz, R. (2010). The effect of activity based instruction on concep-
tual development of seventh grade students in probability. Interna-
tional Journal of Mathematical Education in Science and Techno-
logy, 41, 743-767.
http://dx.doi.org/10.1080/00207391003675158
Gürbüz, R., & Birgin, O. (2012). The effect of computer-assisted teach-
ing on remedying misconceptions: The case of the subject “proba-
bility”. Computers and Education, 58, 931-941.
http://dx.doi.org/10.1016/j.compedu.2011.11.005
Gürbüz, R., Birgin, O., & Çatlıoğlu, H. (2012). Comparing the pro-
bability-related miscon ception s of p upils at dif ferent ed ucatio n levels.
Croatian Journal of Education, 14, 307-357.
Hammer, D. (1996). More than misconceptions: Multiple perspectives
on student knowledge and reasoning, and an appropriate role for
education research. American Journal of Physics, 64, 1316-1325.
http://dx.doi.org/10.1119/1.18376
Jones, G. A., Langrall, C. W., Thornton, C. A., & Timoth y Mogill, A.
(1997). A framework for assessing and nurturing young children’s
thinking in probability. Educa tio na l S tud ies in Ma th ematics , 32, 101-
125.
Jun, L. (2000). Chinese students’ understanding of probability. Unpu-
blished Doctoral Dissertartion. Singapore: National Institue of Edu-
cation, Nan-yang Technological University.
Kahneman, D., & Tversky, A. (1972). Subjective probability: A judg-
ment of representativeness. Cognitive Psychology, 3, 430-454.
http://dx.doi.org/10.1016/0010-0285(72)90016-3
Kazıma, M. (2006). Malawian students’ meanings for probability vo-
cabulary. Educational Studies in Mathematics, 64, 169-189.
http://dx.doi.org/10.1007/s10649-006-9032-6
Keren, G. (1984). On the importance of identifying the correct sample
space. Cognition, 16, 121-128.
http://dx.doi.org/10.1016/0010-0277(84)90002-7
Konold, C ., Pollatsek , A., Well, A ., Lohmeier, J ., & Lip son, A. (199 3).
Inconsistencies in students’ reasoning about probability. Journal for
Research in Mathematics Education, 24, 392-414.
http://dx.doi.org/10.2307/749150
Konold, C. (1989). Informal conceptions of probability. Journal of
Cognition and Instruction, 6, 59-98.
http://dx.doi.org/10.1207/s1532690xci0601_3
Lamprianou , I., & Lampriano u, T. A. (2003). The nature of pupils’ pro-
babilistic thinking in pri mary schools in Cyprus. International Group
for the Psychology of Mathematics Education, 3, 173-180.
Lecoutre, M. P. (1992). Cognitive models and problem spaces in “pu-
rely random” situations. Educational Studies in Mathematics, 23, 557-
568. http://dx.doi.org/10.1007/BF00540060
Memnun, D. S. (2008). Olasılık kavramlarının öğrenilmesinde karşı-
laşılan zorluklar, bu kavramların öğrenilememe nedenleri ve çözüm
önerileri. İnönü Üniversitesi Eğitim Fakültesi Dergisi, 9, 89-101.
Mevarech, Z. R. (1983). A deep structure model of students’ statistical
misconceptions. Educational Studies in Mathematics, 14, 415-429.
http://dx.doi.org/10.1007/BF00368237
Morsanyi, K., Primi, C., Chiesi, F., & Hand l e y , S. (2009). The effects and
side-effects of statistics education: Psychology students’ (mis)conceptions
of probability. Contemporary Educational Psychology, 34, 210-220.
http://dx.doi.org/10.1016/j.cedpsych.2009.05.001
Moyer, P. S., Bolyard, J. J., & Spikell, M. A. (2002). What are virtual
manipulatives? Teaching Children Mathematics, 8, 372-377.
Nilsson, P. (2007). Different ways in which students handle chance
encounters in the explorative setting of a dice game. Educational
Studies in Mathematics, 66, 293-315.
http://dx.doi.org/10.1007/s10649-006-9062-0
Nilsson, P. (2009). Con cep tual v ariati o n an d coo rdin ation in pro bab ility
reasoning. Journal of Mathematical Behavior, 28, 247-261.
http://dx.doi.org/10.1016/j.jmathb.2009.10.003
Offenbach, S. I. (1964). Studies of children’s probability learning be-
havior: I. Effect of reward and punishment at two age levels. Child
Development, 35, 709-715.
Offenbach, S. I. (1965). Studies of children’s probability learning
behavior: II. Effect of method event frequency at two age levels.
Child Development, 36, 951-962. http://dx.doi.org/10.2307/1126936
Olson, J. (2007). Developing students’ mathe matical reasoning through
ga mes . Teaching Children Mathematics, 13, 464-471.
Piaget, J. (1952). The child’s conception of number. New York: Hu-
manities Press.
Polaki, M. V. (2002). Using instruction to identify key features of ba-
sotho elementary students’ growth in probabilistic thinking. Mathe-
matical Think ing and Learning, 4, 285-313.
http://dx.doi.org/10.1207/S15327833MTL0404_01
Pratt, D. (2000). Making sense of the total of two dice. Journal for
Research in Mathematics Education, 31, 602-625.
http://dx.doi.org/10.2307/749889
Sfard, A., Nesher, P., Streefland, L., Cobb, P., & Mason, J. (1998).
Learning mathematics throug h conversation: Is it as go od as they say?
For the Learning of Mathematics, 18, 41-51.
Sharma, S. (2006). How do Pas ifika Students reason about prob ability?
Some findings from fiji. Waikato Journal of Education , 12, 87-100.
Shaughnessy, J. M. (1993). Probability and statistics. Mathematics
Teacher, 86, 244-248.
Shaughnessy, J. M. (1977). Misconceptions of probability: An experi-
ment with a small group, activity-based, model building approach to
introductory probability at the college level. Educational Studies in
Mathematics, 8, 295-316.

R. GÜRBÜZ ET AL.
29
http://dx.doi.org/10.1007/BF00385927
Shaw, D. (1999). Active teaching for active learners. Curriculum Ad-
ministrator, 35, 37-45.
Tatsis, K., Kafoussi, S., & Skoumpourdi, C. (2008). Kindergarten
children discussing the fairness of probabilistic games: The creation
of a primary discursive community. Early Chilhood Education Jour-
nal, 36, 221-226. http://dx.doi.org/10.1007/s10643-008-0283-y
Thompson, P. W. (1992). Notations, principles, and constraints: Con-
tributions to the effective use of concrete manipulativ es in ele mentary
mathematics. Journal for Research in Mathematics Education, 23,
123-147.
Tversky, A., & Kahneman, D. (2003). Preference, belief, and similarity:
Selected writings by Amos Tversky/edited by Eldar Sh af ir. Judgment
under uncertainty: Heuristics and biases (p. 207). Cambridge: The
MIT Press.
Watson, J. M., & Mo rit z, J. B. (2002 ). Sch o o l st u d en ts ’ reasoning about
conjunction and conditional events. International Journal of Mathe-
matical Education in Science and Technology, 33, 59-84.
http://dx.doi.org/10.1080/00207390110087615
Watson, J. M., & Kelly, B. A. (2004). Statistical variation in a chance
setting: A two-year study. Educational Studies in Mathematics, 57,
121-144. http://dx.doi.org/10.1023/B:EDUC.0000047053.96987.5f
Way, J. (2003). The development of young children’s notions of proba-
bility. Proceedings of CERME3, Bellaria.
http://www.dm.unipi.it/cluster-pages/didattica/
Weir, M. W. (1962). Effects of age and instructions on children’s
probability learning. Child Development, 33, 729-735.
Zembat, İ. Ö. (2008). Kavram Yanılgısı Nedir? In M. F. Özmantar, E.
Bingölbali, & H. Akkoç (Eds.), Matematiksel Kavram Yanılgıları ve
Çözüm Önerileri (pp. 1-8). Ankara: PegemA Yayıncılık.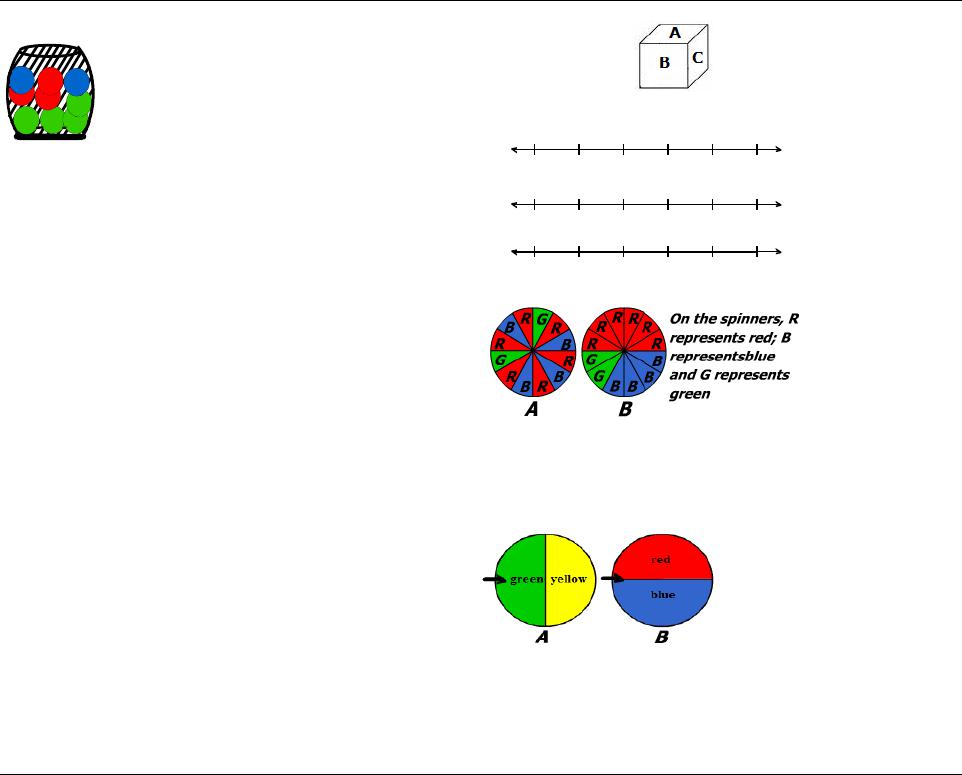

R. GÜRBÜZ ET AL.
30
Appendix
Some Assessment Items
PC 1
There are 4 gr een, 3 red and 2 blue, a tota l of 9 balls in this basket. When
you close your eyes and pick out a ball after mixing all the balls in the
basket, which color will this ball most likely be? Why?
a) Blue
b) Green
c) Red
R 3
A die on whose sides the letters A, B, C, D, E, and F are written is tossed
18 times. Which of the foll ow ing results is more realistical? Why?
PC 2
Musa and Meryem play with a pair of dice. If the sum of the points is 3,
Musa is the wi nner. If the sum of the points is 6, Meryem is the winner.
Which of the f ollowing answ ers seems t o you to be the c or rect one? Why?
a) Musa is the favourite
b) Meryem is the favourite
c) Musa and Meryem have the same chance
PC 4
A and B are two spinners. When these spinners are turned at the
same time, which one is more likely to stop at red? Why?
a) Spinner A
b) Spinner B
c) Both spinners have an equal chance
E 1
When two dice are rolled at the same time, which outcome is mor e likely for
the sum of the numbers on the upper faces of the dice, 2 or 12? Why?
a) 2 is more likely
b) 12 is more likely
c) The probabilities of 2 or 12 are e qua l.
E 4
The rule of the game dictates that when t he spinner s above are turned, if they stop
on yellow or blue ar eas an MP3 player is won by the p layer. There are 50 players
in the competition and the first 3 players turned the spinner A and it stopped
each time on the yellow area . The next 5 people tu rned spinner B and it stopped
each time on the blue area. If it were you, which spinner would you choose? Why?
a) Spinner A
b) Spinner B
c) Both Spinners A or B are the sam e
R 1
A coin is tossed four times and the resul ts are HHH H. What is more likely
for the next toss, H eads or Tails? Why? (T = Tails, H= Heads)
a) H is more likely
b) T is more likely
c) Both have equal chance
R
R
R
B
G
G
O n the balls,
“R” represents red;
“B” represents blue
and “G” represents
green respectively.
G G
B
b)
ABCD EF
a)
c)
x
x
x
xx
x
x
xx
x
x
x
x
x
x
x
x
x
AB
C
D EF
x
x
x
xx
x
x
xx x
xx
x
x
x
x
x
x
ABCD EF
x
x
xx
x
x
xx x x
x
xx
x
xx x x