 Internationa l Journal of Geosciences, 2014, 5, 85-92 Published Online January 2014 (http://www.scirp.org/journal/ijg) http://dx.doi.org/10.4236/ijg.2014.51010 An Improved Met h od of Ret ri evi ng Sea Surface W ind Speed Based on a Four-Layer Medium Model at High Sea States Jiasheng Tian*, Qiaoyun Liu, Wan Pan, Jian Shi The Department of Electronics and Information Engineering, Huazhong University of Science and Technology, Wuhan, China Email: *tianjs@mail.hust.edu.cn Received June 23, 2013; revised July 28, 2013; accept ed August 22, 2013 Copyright © 2014 Jiasheng Tian et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accor- dance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Jiasheng Tian et a l. All Copyright © 2014 are guarded by law and by SCIRP as a guard ian. ABSTRACT Consideri ng about the effe ct of whitecaps and f oams on pulse-limited Radar Altimeters, an improved algorithm of retrieving sea surface w ind speed is proposed in thi s paper. Firstly, a four-layer dielectric model is establ ished in order to simulate an air-sea interface. Secondly, the microwave reflectivity of a sea surface covered by spray droplets and foams at 13.5 GHz is computed based on the established model. These co mputed results show that the eff ect of spray dro plets and fo a ms in high sea sta te c ondit ions s ha ll not be negligible on retrieving sea surface wind speed. Finally, compared with the analytical algorithms proposed by Zhao and some calculated results based on a thre e-layer dielectric model, an improved algorithm of retrieving sea surface w ind spee d is pre se nte d. At a high wind speed, the improved algorithm is in a better accord with some empirical algorithms such as Brown, Young ones and et al., and also in a good agreement with ZT and other algorithms at low wind speed. This new improved alg orithm w ill be suitable not only fo r low wind spe ed retrie val, but also for hig h wind speed retrieval. Better accuracy and effectiveness of wind speed retrieval can also be obtained. KEYWORDS Satellite Altimeter; Wind Speed Retrieving Algorithm; H igh Sea Sta tes; Stratified Media; Whitecap Coverage Rate 1. Introduction Satellite radar altimetry research project could date back to the conference of solid earth and ocean physics held in Williamstown in 1969. After the recent decades, the al- timeter has evolved through Skylab [1], GEOS-3 [2], Seasat and Geosat, Topex/Poseidon and ERS-1 missions. However, the retrieval of the sea surface wind speed from the radar altimeter data poses a great challenge due to the accuracy requirement set forth by the oceano- graphic research community and some applications, such as wind speed measurement with an accuracy of 2 m/s, especially in high sea state conditions. Historically, almost all the altimeter wind speed re- trieving algor ithms (or mode functions) were based on the relationship between the backscattering coefficient and the neutral stable wind speed U10 at 10 meters high above sea level. A large number of wind speed re- trie ving al gorith ms ha s been p ubli shed from 1950s [3-7]. Almost all low speed mode functions tend to overlap whe n the wind speed is about U10 = 10∼7 m/s. This rea- son is that sea states are mainly related to the maximum probability of 10∼7 m/s wind speed. The second pheno- menon is that some high wind speed model functions converge near 9.5 m/s, but spread quickly when the wi nd speed is more than 9.5 m/s. The discrete situation is mainly because most wind speed retrieving algorithms only play an emphasis on the scattering coefficient and neglect wave states (significant wave height, the wave age, etc.) [8-10]. Moreover, for those presented functions, some other factors such as spray droplets, Corresponding author. OPEN ACCESS IJG  J. S. TIAN ET AL. foams and whitecap coverage rate [11] caused by a cyc- lone or hurricane were also not considered about. In 1983, Q. A. Zheng [11] computed the reflectivity of a sea surface covered by whitecaps and foams at 13.9 GHz based on electromagnetic field theory of stratified media, and studied the effect of oceanic whitecaps and foams on pulse-limited rad ar altimeters. In 19 86, Gairola [12] also investigated the reflectivity of a sea surface covered by whitecaps and foams at 13.9 GHz based on a three-layer medium model, and applied the computed result to the sea surface wind speed retrieval. In 2008, Yang [13] also computed a three-layer model for cor- recting backscattering coefficient. When these research results were app lied in retrieving sea surface wind speed, the accuracy would be improved to some extent. Howev- er, in high sea state conditions, some differences from Young algorithm or Brown’s would still exist. In 2003, Zhao and Toba proposed an analysis algo- rithm (referred to as ZT) [6,7] considering about the ef- fect of wave states (or sea states). The algorithm was derived from electromagnetic wave scattering theory and wave spectral theory, and was independent of the spatial and temporal registration data, the size of the measured data and the spatial and temporal data registration stan- dards and so on. The algorithm took the role of wave age into account in retrieving wind speed, and thus its sym- metry was good and its root mean square error could also be accepted. However, for this algorithm, the effect of sea foams and spray droplets was not taken i nto acc ount. The reflectivity in the expression of the ZT function should not be considered to be generated only by the sea water, but a hybrid interface consisting of multilayer media including sea water, foams, spray drop le ts, the a ir . The purpose of this study is to discuss the effect of whitecaps, spray droplets and foams on meas ure ments o f wind speed on pulse-limited rad ar altimeters by calcula t- ing quantitatively the microwave reflectivity of a foam- covered sea surface based on a four-la yer-medium model. The calculated results will be applied into retrieving sea surface wind speed at high sea states. 2. Electromagnetic Scattering from the Sea Surface 2.1. Physical Model The approach for measuring sea surface wind speed by radar altimeter is based on the theory that the sea surface backscattering coefficient is a function of the wind speed. Namely, the usual wind speed retrieval algorithm is based on the direct relationship between wind speed and backscattering coefficient . Based on the specu- lar point theory almost all algorithms (including empiri- cal, semi-empirical or analytic algorithms) can be ex- pressed as [14,15] where is the probability density function of sea surface mean square slopes relating to wind speed. is the reflectivity of the air-to-surface interface at the incident angle θ . The wind speed is re- lated not only to mean square slopes but also to the air-sea interface reflectivity factor . Under the classical assumption that the sea surface mean squre slopes are near ly Gaussian and isotr opic in their distribu- tion, the scatter ing coefficient is given b y ( )( )( )( ) ( ) 2 0 22 2secexp tan RS S θ σθθ θ = − (1) In fact the sea surface process is more complex. In high sea states, sea wave is broken with the high wind speed, an air-sea interface will become a multilayer medium that is made of air, spray droplets(or droplets), foams, and sea water. It is also known that the thickness of the foam and the droplets layer and the coverage rate will vary with the wind speed [16,17]. In 1982, Zheng studied sea foams influence on electromagnetic wave reflection at a normal incident wave, and pointed out that the effect of foams and whitecaps on wave reflection should not be insignificant. However zheng or Gairola only computed the microwave re- flectivity based on a three-layer medium made of air, foams and sea water, and the effect of the spray droplets was neglected. In order to improve the accuracy of es- timated wind speed, it is necessary to establish the electromagnetic wave incidence-reflection physical model in high sea state conditions. Based on the above analysis and experience , in high sea state conditions the air-sea surface should be made up of a four-layer media (Figure 1). The top layer is atmosphere (or air), followed by the sea spray droplet layer. The third layer is foams and the bottom is the seawater layer (Figure 1). The electro- magnetic wave from an altimeter penetrates into the air, and enters into the spray droplet layer and foams, finally plun ges up o n the se a wat er . The e c ho from t he fo ur -layer medium will be received by the altimeter. θ stands for the incident angle, d1 and d2 is the thickness of the droplets and foam layer (Figure 1), respectively. 2.2. Electromagnetic Scattering Theory 2.2.1. TE Wave Let’s suppose that the electric field intensity of an inci- dent wave with the vertical po la r iz a tion is given as 00 sin cos 00 ee jk xjk z j yy yy EE θθ −− −⋅ = == kr E aEaa (2) and p lunges into the four-laye r mediu m at incide nt angle θ . is the unit vector along y direction, k0 is t he wave OPEN ACCESS IJG 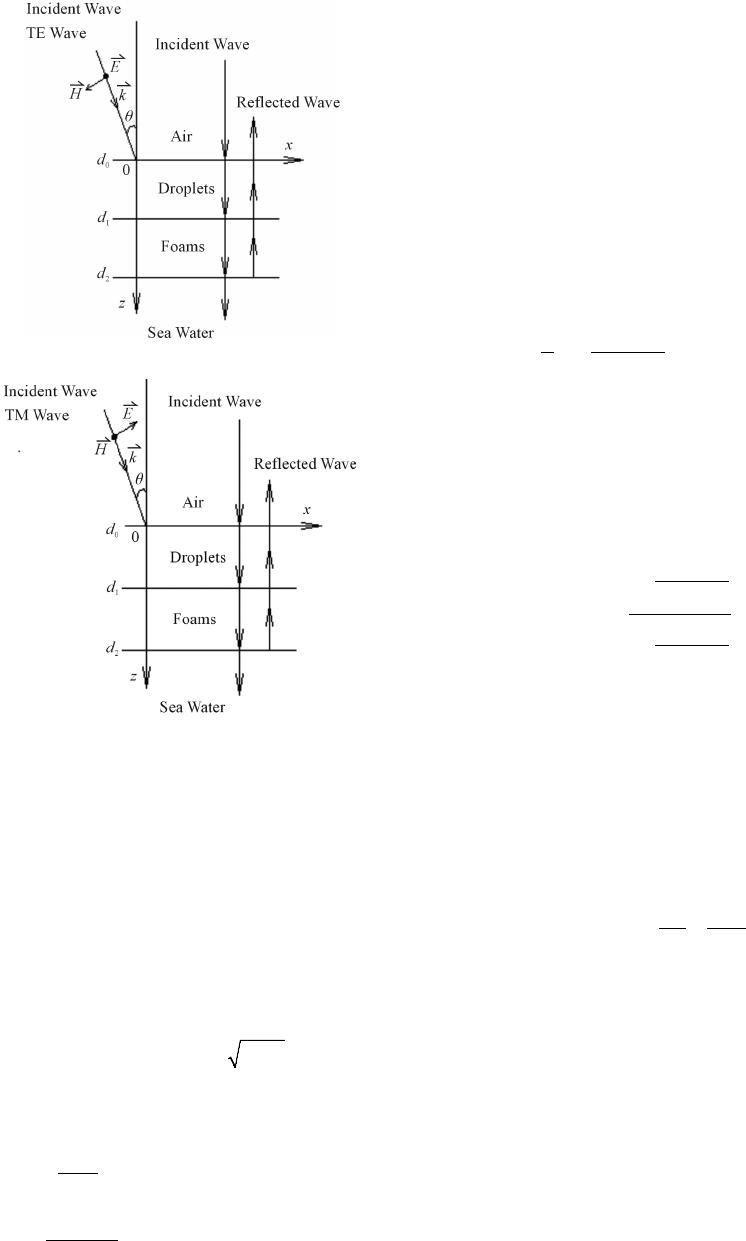 J. S. TIAN ET AL. (a) (b) Figure 1. A multilayer dielectric incident-reflected model. (a) TE wave; (b) TM wave. number in free space. According to electromagnetic theory, electromagnetic waves in the four-layer media can be expressed as the form of the sum of incident wave and reflected wave, that is () sin e ee zmzmm m jk zjk zjkx y ymymm EE E θ −− +− = =+Ea a (3) where m = 0, 1, 2, 3 represent the air layer, the droplets layer, the foam layer and the sea water layer respectively. When m = 3, the second term of Equation (3) is zero in the sea water layer. There , µ m and ε m are the permeability and permittivity, respectively. Accord- ing to the Maxwell equations, we can get the magnetic- field co mponent s given as () sin e ee zmzmmm jkzjkzjk x zm xmm m m k H EE θ ωµ −− +− − = − (4) ( ) sin sin e ee zmzmm m jk zjk zjkx mm zmm m m k H EE θ θ ωµ −− +− = + (5) where θ m is an angle of incidence or refraction. Ob- viously 00 sinsin ,1,2,3 mm k km θθ = = (6) ( ) 2 22 00 sin,1,2, 3 zm m kkk m θ =−= (7) according to electromagnetic theory and the boundary condition which the electromagnetic field tangential components are continuous at the interface, we can get ( ) ( ) ( )() () ()( ) 11 11 1 1 1 e e ee zm m zm m zm mzm m jk d jk dym ym jkdm mjk d ym ym E EN E E ++ ++ − + − ++ + −− + = (8) whe re ( ) ( ) ( ) ( )( ) ( ) ( ) ( )( ) ( ) ( ) ( )( ) ( ) ( )( ) ( ) 11 11 11 11 1 11 ,1 ,1 11 2 ee ee mm zm mzm m mm zm mzm m mzm mm zm m jkd djkd d TE m m jkd djkd d TE m m k Nk R R µ µ ++ ++ ++ ++ + + + − −− + − −− + = + ⋅ (9) and ( ) ( ) ( ) ( ) ( ) 1 1 ,1 1 1 1 ,0,1, 2 1 mzm zm m TE m mmzm zm m k k Rm k k µ µ µ µ + + ++ + − = = + (10) Thus for the four-layer model (Figure 1), we have 00 33 00 33 03 01 1223 03 ee ee zz zz jk djk d yy jk djk d yy EE NNN EE −− ++ −− = (11) Because the thickness of the sea water layer is infinite and there may be considered no reflection wave, we can let d3 = 0 and = 0, and obtain the ratio RTE of the reflecte d wave t o the incident wave at z = 0 (Figure 1(a)). (12) whe re 22 11112 2 2 1,01,01 ,12,23 2 22 ,12 ,23 e ee z z zz jk d upTETETE TE jkdjkdjk d TE TE R RRRR RR − − −− = + ++ and 2 211 112 2 22 1,12,23,01 ,12 22 ,01 ,23 1e e e zz zz jk djkd lowTE TETE TE jkdjk d TE TE R RRRR RR −− −− =++ + d1, d2 is the thickness of the dro plets layer, the foam layer at high wind speed, respectively. d1 and d2 has the rela- tions hi p wit h the wi nd sp ee d U10 at 10 meters height over the sea surface. They can be given as (Andreas E. L., 1995; Wu Jin, 1979) [16,17]. OPEN ACCESS IJG  J. S. TIAN ET AL. (13) ( ) 10 210 10 0.004 7m/s 0.00470.0012 7m/s U dUU ≤ =+ −×> (14) Fro m Equation (12), reflection characteristics of the air-sea interface can be calculated. 2.2.2. TM Wave Let’s suppose that the magnetic field intensity of an in- cident wave with the parallel polarization is given as 00 sin cos 0 e jkx jkz yy yy HH θθ −− = =Ha a (15) Similarl y, the magnetic field i ntensity in the four-layer media can be expressed as the form of the sum of inci- dent wave and reflected wave ( ) 0 sin e ee zm zm my ym jk zjk zjkx y ymym H HH θ −− +− = = + Ha a (16) In the sea water layer (m = 3), the second term of Equ- ation (16) is zero. From Maxwell’s equation, we can get the electric field intensity. In term of electromagnetic field boundary conditions,we can have ( ) ( ) () () () ( )() 11 11 1 1 1 e e ee zm m zm m zm mzm m jk d jk dym ym jkdmmjk d ym ym H HM HH ++ ++ − + − ++ + −− + = (17) whe re ( ) ( ) ( ) ( )() ( ) ( ) ( )() ( ) ( ) ( )() ( ) ( )() ( ) 11 11 11 11 1 11 1 1 11 2 ee ee mm zm mzm m mm zm mzmm mzm mm zm m jkd djkd d mm jkd djkd d mm k Mk R R ε ε ++ ++ ++ ++ + + + − −− + −− − + = + ⋅ (18) and () ( ) ( ) () ( ) 1 1 ,1 1 1 1 1 mzm zm m TMm mmzm zm m k k Rk k ε ε ε ε + + ++ + − = + (19) Thus for the fo ur -layer-model (Figure 1), we have 00 33 00 33 03 01 1223 03 ee ee zz zz jk djk d yy jk djk d yy HH MMM HH −− ++ −− = (20) Letting d3 = 0 and = 0, we can obtain the ratio RTM of the reflected wave to the incident wave at z = 0 (Figure 1 (b)). (21) whe re 22 11112 2 2 2,01,01 ,12 ,23 2 22 ,12 ,23 e ee z z zz jk d upTMTM TM TM jkdjkdjk d TM TM R RRRR RR − − −− = + ++ and 2 211 112 2 22 2,12,23,01 ,12 22 ,01 ,23 1e e e zz zz jk djkd lowTM TMTM TM jkdjk d TM TM R RRRR RR −− −− =++ + From Equation (21), we can discuss the reflection characteristics of the four-layer-medium for TM wave. 2.3. Some Discussions about the Reflected Wave from the Sea Surface In terms of Equations (12) and (21), four curves ( θ = 0˚, 5˚, 10˚, 15˚) of the reflectivity , versu s t he wind speed were plotted (Figure 2). The computed re- sults show that the power reflectivity oscillates when the wind speed is less than 5 m/s or the thickness of spray droplets and foams is less than 0.2 m with the thickness of foams being 0.004 m. Those minmax points (Figure 2) are caused by the resonant absorption of the spray drop- lets layer and the foams layer. When the wind speed is more than 5 m/s, The reflectivity is 0.236 or so. Although the curves (Figure 2) are obtained under some assumed conditio ns (e.g., the incident angle is assumed to be 0˚, 5˚, the temperature is 20˚C.), the curves may represent typi- cal ocean conditions. For a radar altimeter, the incident angle is often less than 5˚, so we can draw a conclusion: ( )() ( ) 22 2 0.2347 0.23720 0.2360 TM TE RR R θθ = ≈ =≈= when θ is less than 5˚, the difference will cause an err ±0.02 dB and is insignificant. However, without whitecaps, the difference will cause an erro of about 4.1 dB in reflected power at normal incident, and will be important for measuring the wind speed on a pulse-limited radar altimeter. So the effect of whitecaps on wind speed retrieval should be considered at a normal incident. 3. The Improved Wind Speed Model Function at High Sea State Conditions 3.1. The Improved Wind Speed Algorithm In term of Equation (12) or (21), the wave reflectivity is a nonlinear function of wind speed. The for- mation of sea spray droplets and foams is related to the wind speed, which can be represented by the whitecap coverage rate wf. The greater the wind speed is, the thicker the droplets layer is, and also the whitecap cov- erage rate wf becomes biger and biger with increasing the OPEN ACCESS IJG  J. S. TIAN ET AL. (a) (b) Figure 2. The reflectivities of TE wave (a) and TM wave (b) ve rsus the wind speed. wind speed. In 1993, Yeli Yuan et al. carried out a de- tailed analysis on sea surface broken process, and ob- tained the analytical expression of whitecap coverage rate wf given as [18]. 4 1.41 10 2.56 10 fs w HU − = × (22) where Hs is the significant wave height, which can be retrieved from the leading curve of the sea surface echo and can also be given as (23) suppose that is the total sea surface reflectivity factor, is the reflectivity factor at the interface be- tween the air, droplets and foams layer, is the reflectivity factor at the interface between the air and sea layer. And thus (24) The analytical expressions of ZT wind speed retrieving algorithm [6,7] is ( ) () ( ) 1 24 22 22 10 0 12 2 10 81 033 2 lnln 22 9 d Dd aag U Ra ak Ck gU β σβ αβ − − ++ ++ =+− (25) in which for K u wave b and , () ( ) 0.6 12 2 10 3.31 , ss gH Uag βγ = = , and γ s is related to sea water density and tension. When the wind speed is more than 2.4 m/s we can take [6] . Substi- tuti ng Eq uation (24) into Equation (25) we can get ( ) ( ) ( ) 2 2 0 4 22 22 10 12 2 10 1 81 33 2 lnln 22 9 fw f d Dd Rw Rw aag Ua ak Ck gU β σ β αβ +− = ++ ++ +− (26) OPEN ACCESS IJG  J. S. TIAN ET AL. It is obvious that the effect of spray droplets, foams on electromagnetic wave reflection plays an important role at wind speed retrieving in Equatio n (26). Ross had so me observations of whitecaps in situ and found that when the wind speed was 20 m/s, the whitecap coverage rate was 21.8% in the Atlantic Ocean. And when the wind speed was 24.7 m/s, the whitecap coverage rate in the visible band was 32% in the Nort h S ea [19]. Obvio usl y, so lar ge a coverage by foam and whitecaps would not be negligi- ble for active microwave remote sensing at high frequen- cies. Therefore, it is necessary that the reflectivity factor of the ZT algorithm s hould be improved to meet with the needs of specific actual sea conditions. Equation (26) is a new improved algorithm presented by the paper. 3.2. The Analysis of the Improved Wind Speed Algorithm For comparison, let us consider the general situation such as wave age β = 1. if the constant α = 0.08, the derived NRCS from Equation (25) is closest to the satellite NRCS on the condition that = 0.3. is thus taken as 0.3 [20,21]. Figure 3 is a comparison chart of Young algorithm (YG), Brown algorithm (BR), ZT algorithm and the proposed improvement algorithm. In Figures 3 and 4, we can find some interesting conclu- sions: 1) At low wind speed (<20 m/s), the proposed im- provement algorithm can agree with ZT algorithm well. This case is expected because whitecap coverage rate is very small. And the change of is so small that it can be ne gligible. 2) At high wind speeds (20 - 40 m/s), the proposed improvement algorithm and ZT algorithm began to di- verge. Thi s case can also be understood because the pro- posed improvement algorithm fully considered about some effects of the spray droplets, foams on electromag- netic wave reflection while ZT algorithm did not. 3) At high wind speeds (20 - 40 m/s), the proposed improvement algorithm is closer to some experienced algorithms such as Brown-fitted curve and Young-fitted curve in high wind-speed range. And in the 20 - 30 m/s range, the proposed improvement algorithm is agreeable well with Young algor ithm (F igure 3). These cases indi- cate that spray droplets and foams make a contributio n to the measurement of radar cross section o f the sea s urface, and influence the retrieval results of wind speed. The presented algorithms in the paper are valid. 4) Although the effect of foams was considered on measurement results of wind speed [11-13], the plotted curve based on a three-layer model diverged distinctly from YG, BR and ZT especially in high wind speeds (Figure 5) . Obvious ly, the four-la yer model in this paper is closer to the practical sea conditions than the three- layer one. It also indicates that the spray droplets layer Figure 3. Several algorithms and the new improved algo- rithm. Figure 4. Differences among several functions at 10 - 40 m/ s . Figure 5. Several algorithms and the new improved algo- rithm. 010 203040 50 6070 -5 0 5 10 15 20 25 wind s peed U 10 (m/s) Backscat teri ng coef fi cient σ 0 (dB ) ZT A l gorithm Improved Algorithm The t hree-layer YG A l gori t hm BR A l gori thm OPEN ACCESS IJG  J. S. TIAN ET AL. makes a contribution to the measurement result of wind speed. The proposed improvement algorithm based on the fo ur -layer model is closer to actual sea surface prac- tice than ZT. 5) We can draw a conclusion that the proposed im- provement algorithm was applicable not only to the low wind speed, but also to the high wind, and also it had a good accuracy. 6) However, there is an inflection po int in the vicinity of 40 m/s in the proposed improvement algorithm (Figure 3), the phenomenon was because the whitecap coverage rate was close to 1 or more than 1 at 40 m/s. When the wind speed is more than 40 m/s, the whitecap coverage rate is 1, and needed further research. 4. Summary The process of an actual sea state is very complex. In high sea states such as typhoon, the air-sea interaction is very strong. When sea surface wind acts on the waves, the sea waves are broken, and thus bubbles emerge on the sea water surface and the foam layer comes into be- ing, and also on the foam layer there is a spray droplet layer. Foams and droplets have a greater influence on electromagnetic wave reflection. In order to consider about this effect, a four-layer media physical model was established to calculate the microwave reflectivity at 13.5 GHz. Based on the model, an improvement algorithm was presented. The proposed algorithm coincided well with ZT algorithm at low speed wind, but began to di- verge at high wind speed. However, the improved algo- rithm was agreeable with some experienced algorithms such as Young algorithm at the high wind speed (20 - 40 m/s). Compared with ZT algorithm and a three-layer model algorithm, this improved algorithm fully consi- dered the specific sea state, and had good precision in high wind speed retrieving. T his algorithm is suitab le not only for the low wind speed retrieving, but also for the high wind speed retrieving. Acknowledgements Thi s re s ea rch wa s f i na nciall y s upp o r t ed b y t h e N a ti o nal Na- tural Scie nce Fo undat ion o f China (Gr ant No. 41076113, Grant NO. 41376181). REFERENCES [1] J. T. McGoogan, L. S. Miller, G. S. Brown and G. S. Hayne, “The S-193 R adar Altimeter Experiment,” Proceedings of The IEEE—PIEEE, Vol. 62, No. 6, 1974, pp. 793-803. [2] H. R. Stanley, “The Geos 3 Project,” Journal of Geo- physi cal Resea rch: Sol id Ea rth (1978-2012), Vol. 84, No. B8, 1979, pp. 3779-3783. [3] D.-L. Zhao and Q. Ye, “On Altimeter wi n d Speed Model Functions and Retrieval of Wave Period,” Journal of Oceanography, Vol. 26, No. 5, 2 004 , pp. 1-11. [4] G. S. Brown, H. R. Stanley and N. A. Roy, “The Wind Speed Measurement Capacity of Space Borne Radar Al- timeter,” IEEE Journal of Oceanic Engineering, Vol. 6, No. 2, 1981, pp. 59-63. http://dx.doi.org/10.1109/JOE.1981.1145484 [5] I. R. Young, “An Estimate of the Geosat Altimeter Wind Speed Algorithm at High Wind Speeds,” Journal of Geo- physical Research, Vol. 98, No. C11, 1993, pp. 20275- 20285. http://dx.doi.org/10.1029/93JC02117 [6] D. L. Zhao and Y. Toba, “A Spectral Approach for De- termining Altimeter Wind Speed Model Functions,” Journal of Oceanography, Vol. 59, No. 2, 2003, pp. 235- 244. http://dx.doi.org/10.1023/A:1025599423405 [7] D. L. Zhao and Y. Toba, “Effect of Wave States o n Alti- meter Wind Speed Algorithm at High Wind Speeds,” The 22nd 267 Asian Conference on Remote Sensing, Singa- pore City, 5-9 November 2001, pp. 1-6. [8] V. Karaev and M. Kanevsky, “Determination of the Near Ocean Surface Wind Speed by Altimeter Data: The First Results, Mathematical Methods in Electromagnetic Theory,” 6th International Conference on Mathematical Methods in Electromagnetic Theory, Lviv, 10-13 Sep- tember 1996, pp. 449-452. [9] J. Gourrion, D. Vandemark, S. Bailey, et al., “A Two- Parameter Wind Speed Algorithm for Ku-Band Altime- ters,” Journal of Atmospheric and Oceanic Technology, Vol. 19, No. 12, 2002, pp. 2030-2048. http://dx.doi.org/10.1175/1520-0426(2002)019<2030:AT PWSA>2.0.CO;2 [10] F. M. Monaldo and E. B. Dobson, “On Using Significant Wave Height and Radar Cross Section to Improve Radar Altimeter Measurements of Wind Speed,” Journal of Geoph ysica l R esearch , Vol. 94, No. C9, 1989, pp. 12699- 12701. http://dx.doi.org/10.1029/JC094iC09p12699 [11] Q. Zheng, V. Klemas, G. S. Haynes and N. E. Huang, “The Effect of Oceanic Whitecaps and Foams on Pulse- Limited Radar Altimeter,” Journal of Geophysical Re- search, Vol. 88, C4, 1983, pp. 2571-2578. http://dx.doi.org/10.1029/JC088iC04p02571 [12] R. M. Gairola and P. C. Pandey, “The Effect of White- caps and Foam on Wind Speed Extraction with a Pulse Limited Radar Altimeter,” Proceedings of the Indian Academy of Sciences, Earth and Planetary Sciences, Vol.95, No. 2, 1986, pp. 265-273. [13] L. Yan g, J. H. Z ou, M. S. Lin and D. L. P an, “Method to Correct Both Foam and Rain Effects Dual Frequency Al- timeter Jason1 Wind Measurements in Typhoon Sh an- shan,” Proceedings of SPIE, Vol. 7105, 2008, pp. 1-11. [14] G. R. Valenzuela, “Theories for the Interaction of Elec- tromagnetic an d Ocean ic Waves—A R eview,” Boundary- Layer Meteorology, Vol. 13, No. 1-4, 1978, pp. 61-85. http://dx.doi.org/10.1007/BF00913863 [15] D. E. Barrick, “Rough Surface Scattering Based on the Specular Point Theory,” IEEE Transactions on Antennas and Propagation, Vol. AP -16, No. 4, 1968, pp. 449-454. http://dx.doi.org/10.1109/TAP.1968.1139220 OPEN ACCESS IJG  J. S. TIAN ET AL. [16] E. L. Andreas and J. B. Edsion, “The Spray Contribution to Net Evaporation from the Sea: A Review of Recent P rog re ss ,” Boundary-Layer Meteorology, Vol. 72, No. 1-2, 1995, pp 3-52. http://dx.doi.org/10.1007/BF00712389 [17] J. Wu, “Oceanic Whitecaps and Sea State,” Journal of Physical Oceanography, Vol. 9, No. 5, 1979, pp. 1064- 1068. [18] E. C. Manahan, et al., “Optimal Po we r -Law Description of Oceanic Whitecap: Coverage Dependence on Wind Speed , ” Journal of Physical Oceanography, Vol. 10, No. 12, 1980, pp. 2094-2099. http://dx.doi.org/10.1175/1520-0485(1980)010<2094:OP LDOO>2.0. CO; 2 [19] D. B. Ross, et al., “Observations of Oceanic Whitecaps and Their Relation to Remote Sensing Measurements of Surface Wind Speed,” Journal of Geophysical Research, Vol. 79, No. 3, 1974, pp. 444-452. http://dx.doi.org/10.1029/JC079i003p00444 [20] F. C. Jackson, W. T. Walton, D. E. Hines, B. A. Walter, et al., “Sea Surface Mean Square Slope from Ku-Band Backscatt er Data,” Journal of Geophysical Research, Vol. 97, No. C7, 1992, pp. 11411-11427. [21] E. J. Walsh, D. C. Van demark, C. A. Friehe, S. P. Burns, D. Khelif, R. N. Swift , et al., “Measurements Sea Surface Mean Square Slope with a 36-GHz Scanning Radar Alti- meter,” Journal of Geophysical Research, Vol. 103, No. C6, 1998, pp. 12587-12601. http://dx.doi.org/10.1029/97JC02443 OPEN ACCESS IJG
|