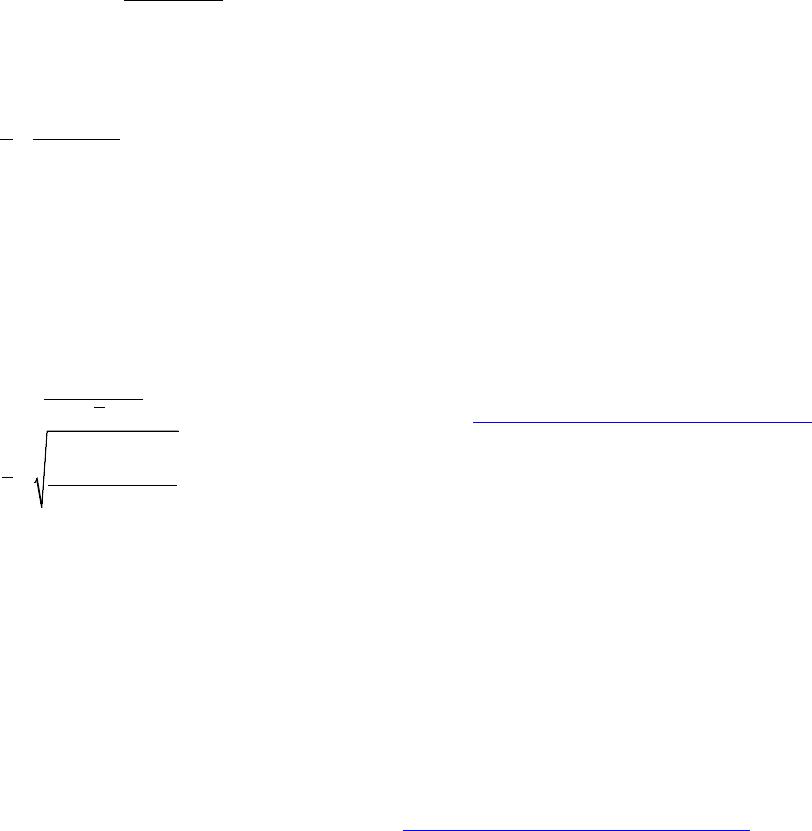
D. BOUNAZEF ET AL.
cess of the manufacturing company of tubes. The capa-
bility index that takes account process, machine, and the
performance is calculated as follows:
( )
UCL LCL
Index, ,6
pmp
CCP
σ
−
=
(13)
The val ue of t hi s i nd e x i s t he n 0 , 9 999 9 3 , i. e . close to 1.
The capability index of the process Cp is found in the
following manner:
3.2076447 1.0692149
33
p
z
C= ==
(14)
The Cp index exceeds the value of 1, but the quality of
process 6σ requires a capability of process more than 2.
The production process of the tubes is barely capable but
is not very efficient. The capability index of Machine Cm
allows measuring the material resources available the
continuous production process of the tubes is able to
achieve the target of 99.999966% of performance; the
value of this ind e x is :
( )
2
1
UCLLCL;
3
target
;
1
0.6292
m
n
i
i
m
C
x
n
C
σ
σ
=
−
=
−
=−
=
∑
(15)
The Cm index does not exceed 1.11 which allows the
reduction of waste of 0.00034%. The tools and machin-
eries of production plant are not capable to achieve per-
formance of 6σ quality. The plant must innovate and re-
duce the variability due to different causes of machine
stops.
15. Conclusion
Causes a nalysis of wa ste by 2 methods statistica l process
control and design of experiments are a very effective
means that can take me asures to manage the losses.
These methods permit to develop recommendations.
They can satisfy demands to achieve the production re-
quirements mastering the c ontrollab le factors, reducing
the impact of uncontrollable factors, minimising the fi-
nancial losses and improving the quality of production.
The reduction of waste is the result of the reduction of
machine stops; this reduction supports the achievement
of measurable and non-measurable gains such as reduc-
tion of the manufacturing cost and coast of control fac-
tors, reduction delay time, improvement employee com-
petence, improvement working environment due to the
reduction of machine stops hours. All this will automati-
cally change the pr ofitability of the process and the gains
of the company. The performance of production is treat-
ed in sigma process quality (performance quality) by
Equation (10).
REFERENCES
[1] P. Bousselet, “The process Computerisation QSE in Ag-
ribusiness: The 30 Questions to Consider Quality, Safety
and Environment,” PBC Soft, Paris, 2010.
[2] B. F r o ma n, J. M. Gey and F. Bonnifet, “Quality, Safety
and Environment: Construct an Integrated Management
Sys te m, ” AFNOR, La Plaine Saint-Denis, 2007.
[3] M. Bernardo, M. Casadesus and S. Karapetr ovic, “How
Integrated Are Environmental, Quality and Other Stan-
dardised Management Systems? An Empirical Study,”
Journal of Cleaner Production, Vol. 17, No. 8, 2009, pp.
742-750. http://dx.doi.org/10.1016/j.jclepro.2008.11.003
[4] K. R. Bhote, “The Po wer of Ultimate Six Sigma, Quality
Excellence t o To tal B usi ness E xc el len ce,” Amacom, New
York, 2003.
[5] D. Duret and M. Pillet, “Quality in Production: From ISO
9000 to Six Sigma,” 4th Edition, Eyrolles Edition, Paris,
2005.
[6] H. Aadi and B. John, “Hygiene and Safety at Work,”
Office of Professional Training and Work Promotion,
Rabat, 2011.
[7] Fernand ez-Toro and A. H. Schauer, “Management of
Information Security: Implementing ISO 27001, Imple-
mentation of ISMS and Certification Audit,” Eyrolles,
Paris, 2008.
[8] R. Holdsworth, “Practical Applications Approach to De-
sign, Development and Implementation of an Integrated
Management System,” Journal of Hazardous Materials,
Vol. 104, No. 1-3, 2003, pp. 193-205.
http://dx.doi.org/10.1016/j.jhazmat.2003.08.001
[9] T. H. Jorgensen, A. Remmen and M. D. Mellado, “Inte-
grated Management Syste ms —Three Levels of Integra-
tion,” Journal of Cleaner Production, Vol. 14, 2006, pp.
713-722.
[10] R. Salomone, “Integrated Management S ys t em s : Experi-
ences in Italian Organisations,” Journal of Clearner Pro-
duction, Vol. 16, 2008, pp. 1786-1805.
OPEN ACCESS OJBM