 Intelligent Information Management, 2011, 3, 49-55 doi:10.4236/iim.2011.32006 Published Online March 2011 (http://www.SciRP.org/journal/iim) Copyright © 2011 SciRes. IIM Semi-Markovian Model of Unreliable Control of Restorable System with Latent Failures Yuriy E. Obzherin, Aleksei I. Peschansky, Yelena G. Boyko Sevastopol National Technical University, Sevastopol, Ukraine E-mail: vmsevntu@mail.ru Received December 27, 2010; revised January 3, 2011; accepted January 5, 2011 Abstract Semi-Markovian model of control of restorable system with latent failures has been built with regard to con- trol errors. Stationary reliability and efficiency characteristics of its operation have been found. The problem of control execution periodicity optimization has been solved. Keywords: Control, Control Errors, Latent Failure, Semi-Markovian Process, System Stationary Characteristics 1. Introduction An important factor providing reliability, high quality, and efficiency of technological complexes is the presence of control systems in them. The reviews of the results concerning control model building are contained in [1,2]. In the present article the model of control execution and restoration of a single-unit system with latent fail- ures has been investigated under the condition of control errors occurrence. The latent failure is the one that does not show up till the control is executed. While control is executed errors of first and second kinds are possible [3]. It reduces technological complex operation efficiency. In the work [4] the model of control of the system with possible failures was studied, but there reliability charac- teristics were defined under the assumption of exponential distributions of random values characterizing the system. The problems of technological complexes’ control are closely connected with their maintenance. In the work [5] maintenance models were built by means of semi- Markovian processes with a common phase field of states [6]. In the present article this apparatus is used to build the model of control under the condition of latent failures occurrence. And herewith, random values char- acterizing the system are supposed to have distributions of general kind. 2. The Problem Definition and Mathematical Model Building Let us investigate the system operating in the following way. At the time zero the system begins operating, and the control is on. System failure-free operation time is a random value (RV) with distribution function (DF) tP t and distribution density (DD) t. The control is executed in random time with DF Rt Pt and DD rt. The failure is detected only when control is carried out. Control duration is RV with DF tVt P and DD vt. When the control is on, the system does not operate. After failure detection system restoration begins immediately and the control is deactivated. System restoration time is RV with DF Gt Pt and DD t. After the system restoration all its properties are completely re- stored. All the RV are supposed to be independent, have finite assembly averages and variances. While control execution errors of first and second kinds can take place. Control system error of first kind lies in regarding system in up state as a failed one (false failure). The probability of such an errror is equal to р1. The error of second kind is taking system’s good state for bad one (failure omission). The probability of such an error is equal to р0. The purpose of the present article is to find stationary reliability and economical characteristics of the sin- gle-unit restorable system under the condition of latent failures occurrence, with regard to control errors. To describe the system operation let us use semi- Markovian process t with the following field of states: 111, 212, 211,101, 202, 201, 200, 210Еххх,  Y. E. OBZHERIN ET AL. 50 ; ; where 111 means the system has been restored, the control is activated; 212х - control has begun, the system is in up state, it does not operate during control execution, time х is left till the latent failure (regardless of deactivation time); 211х - control has ended, the system in up state has been treated correctly and continues to operate, time х is left till the latent failure; 101 х - latent failure has occurred, time х is left till control execution; 202 - control has begun, the system is in a state of la- tent failure, it does not operate; 201 - control has ended, failed system is regarded as the one in up state (error of second kind), its operation has begun; 200 - control has ended, failed system is regarded as a failed one, system restoration has begun, control is deac- tivated; 210 - control has ended, system in up state is taken for failed one (error of first kind), system restoration has begun, control is deactivated; Time diagram of the system operation is repre- sented in the Figure 1. And in the Figure 2 the system transition graph is given, where a set of up states is, is a set of down states. E E Time diagram of the system operation and the system transition graph are shown in Figure 1 an d Figure 2 respectively. Let us define the probabilities of the embedded Mark- ovian chain (EMC) transitions: ,0 nn 212 111 0 101 111 0 101 211 212 211 ,0 ,0 ,0; ,0 ; x x y x y x pfxtrtdtx prxtftdtx prxyy prxyyx (1) 211 210 2121 2121 202202111 111 101201200210 201 200 2020 2020 ,; 1; ,1, x xx x ii PpPp PPPP PpPpp pi 0,1. Let us indicate , 111 202 , , 201 210 , the values of EMC stationary distribution for the states 111, 202, 201, 210, 200 respec- tively and assume the existence of stationary densities 200 ,0n n 212 , 211 , 101 212x 111 211x202 201 202 200210 111 212x t t t 1 K s х х 111 101х Figure 1. Time diagram of the system operation. 111 211x 212x 210 101x 202 200 201 + - Figure 2. System transition graph. 0 0 x 1 0 x 0 0 0 1 0 0 0 0 111200210 , 212 111 211 , 211212 , 101 111 211 , 202101201 , 201202 , 200202 , 210212 , 2202 201212 211 fxtrtdt yryx dy xp x xftrxt yryx dy xdx p p px dt dx x 0 101 1.dxx dx (2) The last equation of the system (2) is a normalization requirement. To solve the system (2) let us exclude the function 211 from the second and third equations: 01 0 212 212 x х xtrtdt pyryxdy (3) for the states 212 , 211 , 101 respectively. Now we can make the system of integral equations for them: Copyright © 2011 SciRes. IIM  Y. E. OBZHERIN ET AL. Copyright © 2011 SciRes. IIM 51 Let us indicate 1 212х , then the Equation (3) will take the form: Let us introduce the function 1 rxp rx and the integral operator r x xryxyd y . 10 11 х x хftrt хdt yr yxdy (4) Then the Equation (4) can be rewritten in the following way: 0 11 1 rr Af p . The solution of this equation will be defined with the help of method of successive approximations. The solution of this equation is defined by the formula 0 10 110 1 212 , rr x х hyxfydyhyfxydy pp (5) where is the density of renewal function r ht r t generated by the RV with improper DF 1 pRtRt ; * 1 n rn htr t , where *n rt is n-fold convolu- tion of the function . 1 rtp rt Using Formula (5), one can define the rest of station- ary densities 0 0 1 00 211, 101,, rr h yfx ydyxfzzxdz p (6) where 0 , rr zxr xzr xyhzydy is the ated by RV with improper distribution density rt . The values of stationary distribution for the states 210, 202, 201, 200 are defined from the system (2): density of direct residual time of renewal process gener- 11 00 10100 011 00 01 1 00 1 210, 2021, 2011, 2001. rr rr pp H zfzdzH zfzdz ppp ppp zf zdzHzf zdz pp p (7) Here * 0 n rn tR t , where *n Rt is n-fold tionary operation time T , mean stationary restoration time T , stationary availability function Kг. convolution of the function . The constant Rt 0 is found with the help of normalization requirement. The sets of up states and down states EE are the following ones: 111,211,212, 101,202,201,200,210.ExExx 3. Definition of System Stationary Characteristics Mean stationary operation timeT and mean sta- tionary restoration tim T e can be found with the help of Formula [6 Let us define system stationary characteristics: mean sta- ]: , ,, ЕE EE me deme de ТT. eE dePeE de (8) Here is the EMC de ,0 nn stationary dis- tribution; are mean values of system dwelling times; me , eE are the probabilities of EMC ,0 nn transitions from up into down states. Mean values of system dwelling times in the states are: 00 111; 211; 212202; 201; 101;210200 mFtRtdtmxRtdtmxm mМmxхmmМ (9)  Y. E. OBZHERIN ET AL. Copyright © 2011 SciRes. IIM 52 With regard to Formulas (5-7) and (9) one can define the functionals contained in (8): 00 0000 1 00 0 1000 0 00 00 00 1100 , ,2111, 11 x r E y rr r E r E medeF t Rt dtdxRt dthyfxy dy p Ft R t dtFy dyhyt R t dtMHy Fy dy p PeEdexdxHzf zdz m edeMdxhyfxydyx pp 00 0 111 000 01 011000 1 000 111 0000 1 0 010 , 1111 11 , 11 rrr rr r dxzxfzdz p ppp MHzfzdzMHzfzdzMHzfzdz pp ppp p MHzfz dzMHyfy dyfz dzxzxdx ppp p MHzfzdz pp 00 1 000 01 100 01 1 000000 100 1 0 0 1 11 . rr r r pp p1 p Hzfzdz MMHzfzdz pp p pp p MHzfzdzMMMMHxFxdx pppp Thus, mean stationary operation time is defined by the ratio T 1 10 0 , 1 r r p FyH ydy p T FzdHz (10) and mean stationary restoration time is determined by the formula: T 01 1 01 01 0 0 0 1 1 rr r pp p MFzdHzMMMMHtF pp pp T FzdHz tdt (11) Stationary availability function is found from the ratio г КТТТ . We get 1 10 01 01 0 0 () () 1 () () г r r К p MFyHydy p pp MFzdHzMM pp p M (12) Important characteristics for system operation quality testing are economical criteria, such as mean income S per unit of calendar time and mean expenses C per time unit of system’s up state. To define them let us use the Formula [7]: s E E c E E mеfеdе Smеdе mеfеdе Cmеdе , (13)  Y. E. OBZHERIN ET AL.53 where , sc fе e are the functions defining income and expenses in each state respectively. Let c1 be the income received per time unit of sys- tem’s up state; c2 - expenses per time unit of restoration; c3 – expenses per time unit of control; c4 are wastes caused by defective goods per time unit of latent failure. For the given system the functions , sc fе e are the following: 1 22 33 44 ,111,211 ,0,111,211 , ,200,210,,220, 210, , 212,202,, 212,202, ,101 ,201,,101 ,201. sc се хeх се сe fe fe се хсeх cех ce х (14) With regard to (13) and (14) mean income is defined by the ratio 01 1 14 23414 001 1 00 01 001 0 1 ()()()()() ()() 1() ()() rr r pp p cccMcMcMFzdHzccFtHtdt ppp p Spp MM MMFzdHzM ppp and mean expenses are determined by the ratio 01 1 24 431434 011 0 00 1 10 1 rr r pp p cMcMcMcMFzdHzccF tHt dtcMcM ppp p Cp MFtHtdt p Let us consider the case of non-random control execu- tion periodicity 0 . Taking into account that in this case 1Rtt , where const , stationary avail- ability function is defined by the formula (1) 1 1 01 1 1 001 1 1 n n nn г n n MpFtdt Кpp MM pF ppp n (15) mean income can be defined in the following way 1 01 1423 413 4141 11 01 0 01 1 1 001 11 1 n nn nn n n n pp c ccMcMcpFncMcccpFtdt pp p Spp MM pFnM ppp (16) mean expenses are found with the help of the ratio 1 01 24 43114134 11 01 0 1 1 1 1 1 1 n nn nn n n n nn pp cMcMccMpFnccpF t dtcMc pp p C MpFtdt (17) Copyright © 2011 SciRes. IIM  Y. E. OBZHERIN ET AL. 54 Let us investigate some special cases of the system op- eration. If errors of one kind only occur, two cases are possible. Let p= 0, p≠ 1, then Formulas (10-12) take the form 0 0 1 1 r p MFyHydy p 0 0 11 1 00 10 00 , 1 1 , 11 r rr r г rr T FzdHz pp MMFzdHzMMHtFtdtMFyHydy pp TК FzdHz MFzdHzM If , then 10 0, 1pp rt rt , rr tHt with DF is renegeneratwal function ed by RV Rt , * 0 n rn tR transformed into t. In this case Formulas (10-12) are 0 1 0010 000 , 1 1 ,. 1 1 r rr г rr T FzdHz p MMFzdHz MMMFyHydy pp TК FzdHzMMFzdHz M p In case of reliable control 01 0pp system sta-tionary characteristics are defined by the ratios 0 1 010 00 , 1 1 , 11 r rr г rr M T FzdHz p MMFzdHzMMMFyHydy p TК FzdHz MFzdHzM which coincide with ones found for a single-component stem with reliable control. rol Execution ontrol execution periodicity optimiza- on is reduced to analysis of extremums of the system us suppose RV , and of to have Erlangian distri- bution. For the calculation optimal value opt sy pro- nd viding maximal mean income S per calendar time unit aof optimal value opt s opt c providing minimal mean expenses opt C per time unit of system’s good state, the following initial data have been take1 = 2 c.u./h; с2 = 2 c.u./h; с3 = 1 c.u./ c.u./h. The results of these calculations are represented in the Table 1. The graphs of s c n: с h 4. Optimization of Cont Periodicity e problem of c; funct с4 = 1 ion г K , ,S C for the case of Erlangian distribution of the 2nd order and 10,3,p 00, 25p are shown in Figures 3, 4 and 5. 5. Conclusions pparatus of semi-Markovian proce Th ti characteristics Кг, S, C as functions of a single variable . Using Formulas (15-17), one can define an optimal ripeod of control of the system investigated for different distribution laws of random values. The initial data for calculations of optimal values of control periodicity are: mean time of failure-free operation , mean restora- tion time , control duration . For example, let U co sing an a mm s ne ses with a reliability on phase field it is possible to defi Copyright © 2011 SciRes. IIM 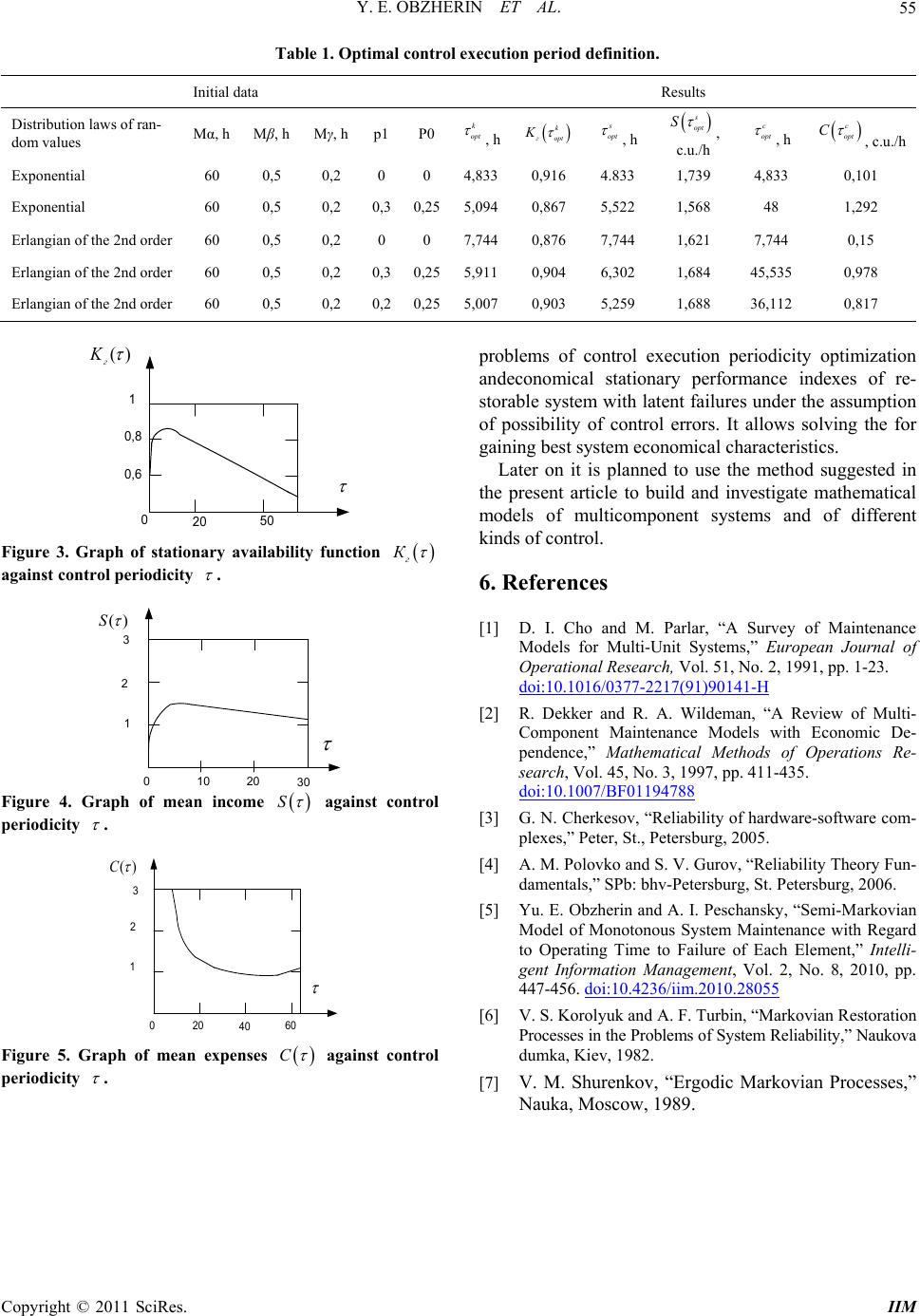 Y. E. OBZHERIN ET AL.55 Table 1. Optimal control ex Initial data ecution period definition. Results , h s opt S , c.u./h c opt , h c opt C Distribution laws of ran- dom values β, h Mγ, h p1P0 , h k гopt K opt Mα, hMk opt , c.u./h Exponential 60 0,5 0,2 0 0 4,8330,916 4.833 1,739 4,833 0,101 Exponential 60 0,5 0,2 0,30,255,0940,867 5,522 48 1,292 Erlangian of the 2nd order 60 0,5 0,2 0 0 7,7440,876 7,744 1,621 7,744 0,15 Erlangian of the 2nd order 60 0,5 0,2 0,30,255,9110,904 6,302 1,684 45,535 0,978 Erlangian of the 2nd order 60 0,5 0,2 0,20,255,0070,903 5,259 1,688 36,112 0,817 1,568 )( г 020 50 1 0,8 0,6 Figure 3. Graph of stationary availability function г К against control periodicity . )( S 3 2 1 0210 Figure 4. Graph of mean income 0 30 S against control periodicity . 2 1 0620 40 3 0 )( Figure 5. Graph of mean expenses C against contro periodicity l . proble coexe pey option andeconomical stationary performance indexes of re- ematical m d M. Parlar, “A Survey of Maintenance ti-Unit Systems,” European Journal of ms ofntrol cutionriodicittimiza storable system with latent failures under the assumption of possibility of control errors. It allows solving the for gaining best system economical characteristics. Later on it is planned to use the method suggested in the present article to build and investigate math odels of multicomponent systems and of different kinds of control. 6. References [1] D. I. Cho an Models for Mul Operational Research, Vol. 51, No. 2, 1991, pp. 1-23. doi:10.1016/0377-2217(91)90141-H [2] R. Dekker and R. A. Wildeman, “A Review of Mu Component Maintenance Models w lti- ith Economic De- pendence,” Mathematical Methods of Operations Re- search, Vol. 45, No. 3, 1997, pp. 411-435. doi:10.1007/BF01194788 [3] G. N. Cherkesov, “Reliability of hardware- plexes,” Peter, St., Petersbu software com- rg, 2005. Petersburg, 2006. d [4] A. M. Polovko and S. V. Gurov, “Reliability Theory Fun- damentals,” SPb: bhv-Petersburg, St. [5] Yu. E. Obzherin and A. I. Peschansky, “Semi-Markovian Model of Monotonous System Maintenance with Regar to Operating Time to Failure of Each Element,” Intelli- gent Information Management, Vol. 2, No. 8, 2010, pp. 447-456. doi:10.4236/iim.2010.28055 [6] V. S. Korolyuk and A. F. Turbin, “Markovian Restoration Processes in the Problems of System Reliability,” Naukova 989. dumka, Kiev, 1982. [7] V. M. Shurenkov, “Ergodic Markovian Processes,” Nauka, Moscow, 1 Copyright © 2011 SciRes. IIM
|