J. Biomedical Science and Engineering, 2011, 4, 187-195 JBiSE
doi:10.4236/jbise.2011.43026 Published Online March 2011 (http://www.SciRP.org/journal/jbise/).
Published Online March 2011 in SciRes. http://www.scirp.org/jour nal/JBiSE
In vivo dynamic image characterization of brain tumor growth
using singular value decomposition and eigenvalues
Murad Shibli
Department of Mechanical Engineering, College of Engineering, United Arab Emirates University, Al Ain, United Arab Emirates.
Received 3 December 2010; revised 25 January 2011; accepted 30 January 2011.
ABSTRACT
This paper presents a dynamic image approach to
characterize the growth of brain cancer invasion of
tumor gliomas cells using singular value decomposi-
tion (SVD) technique. Such a dynamic image is iden-
tified by the white and grey matter displayed by mag-
netic resonance (MR) images of the patient brain
taken at different times. SVD components and prop-
erties have been analyzed for different brain images.
It is figured out that the growth of tumor cells is
quantized by the SVD eigenvalues. Since SVD geo-
metrically interprets an ellipsoid transformation,
then the higher the eigenvalues, the more of tumor
growth is. In vivo SVD dynamic imaging offers a
more predictive model to assess the tumor therapy
than conventional technologies. Furthermore, an ef-
ficient dynamic white-black indicator of the tumor
growth rate is constructed based on the change in the
diagonal eigenvalues matrices of two MR images
taken at different times. Finally, SVD image process-
ing results are demonstrated to verify the effective-
ness of the applied approach that can be imple-
mented for each individual patient.
Keywords: Brain Cancer; Tumor Image Identification;
Singular Value Decomposition
1. INTRODUCTION
A brain tumor is defined as an intracranial solid neo-
plasm within the brain or the central spinal canal. It is
created by an abnormal and uncontrolled cell division,
normally either in the brain itself or in the cranial nerves.
Any brain tumor is inherently serious and life-threaten-
ing because of its invasive and infiltrative character in
the limited space of the intracranial cavity. For this rea-
son, brain tumor has received a great attention. A novel
method for quantifying the speed of invasion of gliomas
in white and grey matter from time series of magnetic
resonance (MR) images was presented in [1]. The pro-
posed approach was based on mathematical tumor growth
models using the reactiondiffusion formalism. The quan-
tification process was formulated by an inverse problem
and solved using anisotropic fast marching method
yielding an efficient algorithm. It was tested on a few im-
ages to get a first proof of concept with promising results.
In CT images, tumors located in a liver are generally
identified by intensity difference between tumor and
liver. The intensity of the tumor can be lower and or
higher than that of the liver. However, the main problem
of liver tumor detection from CT images is related to
low contrast between tumor and liver intensities. Tumor
sometimes presents in a very small dimension and makes
the detection even more difficult. Work [2] focused on
contrast enhancement of CT images containing liver and
tumor based on the histogram processing as a necessary
preprocessing for liver tumor identification. Results
showed that using this proposed method, the contrast of
the CT images can be enhanced and results in relatively
accurate identification of tumors in the liver.
Difficulties are encountered in identifying small liver
cancers during surgery. Fluorescent imaging using indo-
cyanine green (ICG) has the potential to detect liver can-
cers through the visualization of the disordered biliary
excretion of ICG in cancer tissues and noncancerous
liver tissues compressed by the tumor. In cancer research
work [3], ICG had been intravenously injected for a rou-
tine liver function test in 37 patients with hepatocellular
carcinoma (HCC) and 12 patients with metastasis of
colorectal carcinoma (CRC) before liver resection. Sur-
gical specimens were investigated using a near-infrared
light camera system.
The aim of report [4] scan was to identify the different
genomic tests that are being promoted for clinical use in
cancer prevention, diagnosis, and management. As out-
lined in the detailed work plan, the project was organ-
ized into two distinct parts with separate aims and
methodologies. The goal of Part I was to answer the key
question: What genetic tests are currently available for
cancer prevention, diagnosis and treatment? The goal of

M. Shibli / J. Biomedical Science and Engineering 4 (2011) 187-195
188
Part II of this project was to answer the key question:
What genetic tests are in development for cancer?
To assess the value of pelvic-phased array (PPA) dy-
namic contrast-enhanced magnetic resonance imaging
(DCE-MRI) in predicting intraprostatic tumour location
and volume for clinically localized prostate cancers in
[5]. Suspicious areas on prospective prebiopsy MRI
were located with respect to anatomic features, gland
side, and transition zone (TZ) and peripheral zone (PZ)
boundaries. These MRI findings were compared with
histopathology findings for the radical prostatectomy
specimens. Literature review of original studies corre-
lating MRI and histologic results was performed.
DCE-MRI with a PPA is superior to T2-weighted se-
quences for the detection and depiction of intraprostatic
prostate cancer.
Singular Value decomposition (SVD) was presented in
[6] along with some related comments on numerical de-
termination of rank. A variety of applications of SVD in
linear algebra and linear systems is then outlined [7].
Some details of implementation of the SVD on a digital
computer are discussed. Five combinations of im-
age-processing algorithms were applied to dynamic in-
frared (IR) images of six breast cancer patients preop-
eratively to establish optimal enhancement of cancer
tissue before frequency analysis [8]. Mid-wave photo-
voltaic (PV) IR cameras with 320 × 254 and 640 × 512
pixels were used. The signal-to-noise ratio and the
specificity for breast cancer were evaluated with the im-
age-processing combinations from the image series of
each patient. Before image processing and frequency
analysis the effect of patient movement was minimized
with a stabilization program developed and tested in the
study by stabilizing image slices using surface markers
set as measurement points on the skin of the imaged
breast. A mathematical equation for superiority value
was developed for comparison of the key ratios of the
image-processing combinations.
In this proposed paper SVD components and proper-
ties have been analyzed for different brain images. It is
figured out that the growth of tumor cells is quantized by
the SVD eigenvalues. Since SVD geometrically inter-
prets an ellipsoid transformation, then the higher the
eigenvalues, the more of tumor growth is. Furthermore,
an efficient dynamic white-black indicator of the tumor
growth rate is constructed based on the change in the
diagonal eigenvalue matrices of two MR images taken at
different times. This paper is organized as follows. Sec-
tion 2 summarizes modeling of tumor modeling. SVD of
tumor images is introduced in section 3. Dynamic image
modeling and results of white-gray matter are presented
in section 4. Mouse Tumor Model is introduced in sec-
tion 5. Section 6 discusses the advantages, disadvantages
and a comparison of the methodology with other ap-
proaches. Finally, conclusions are demonstrated.
2. TUMOR GROWTH MODELING
In cancer treatment, understanding the aggressiveness of
the tumor is essential in therapy planning and patient
follow-up. A method for quantifying the progression of
the critical target volume (CTV) of glial-based tumors,
on the basis of their growth dynamics was proposed in
[1,9]. The formulation is based on the tumor growth
model proposed which uses reaction-diffusion formalism:


2
uCx uuu
t


 
 (1)
 
,
,
g
ww
d Igraymatter
Cx d Cxwhitematter


 (2)
where


ut can be seen as the normalized tumor cell
density of a tumor at a given point,

Cx is the diffu-
sion tensor explaining the invasion of tumor cells, and

is the proliferation rate. The matrix


Cxdefines
anisotropic diffusion on the white matter following the
main fiber directions and isotropic diffusion on the grey
matter, where


w
Cx is the water diffusion tensor ob-
tained from MR diffusion tensor imaging. The speed of
invasion is determined by the diffusion coefficients
g
d
and w d in grey and white matter respectively. These
parameters for each patient can be identified using im-
ages taken at two different times. One crucial observa-
tion is that explicit derivatives of C with respect to the
variables are not available.
With the proposed method, quantitative estimates
were obtained for the speed of invasion in white and
grey matter by solving the patient specific parameter
identification problem for this growth model using MR
images taken at two different time instances, t1 and t2,
from the same patient. The parameter identification
problem was formulated using the front approximation
of reaction-diffusion equations, which resulted in ani-
sotropic Eikonal equations. The anisotropic fast march-
ing method proposed in [1,10] is used for numerical so-
lutions yielding an efficient algorithm.
The model given above requires tumor cell density


ut to be known at every point as an initial condition.
However, this is not the case for medical images where
only contours around gross tumor volume (GTV) and
CTV are available. The front motion approximation of
reaction-diffusion equations offers a solution for this
discrepancy between information needed and observa-
tions available [1,9].
3. SINGULAR VALUE DECOMPOSITION
Let A be a mn

real matrix; m and n may be any

M. Shibli / J. Biomedical Science and Engineering 4 (2011) 187-195
189
positive integers. The SVD of
A
is the factorization
T
mnmnnn nn

A
USV (3)
where

1
diag,,n
s
sS.
The i
s
’s are called the singular values of A. By
convention, they are ordered so that 12 0
n
ss s.
The singular values of A are the square roots of the
nonzero eigenvalues of T
A
A or T
A
A.
• The vectors

1,, n
uuare called the left singular
vectors ofA. Left singular vectors ui are the ei-
genvectors of T
A
A. These are unit vectors along
the principal semi-axes of
A
S.
• The vectors

1,, n
vvare called the right singu-
lar vectors of A. Right singular vectors vi are the
eigenvectors of T
A
A.These are the preimages of
the principal semi-axes, defined so that
,1,2,,
iii
vsui nA (4)
T,1,2,,
iii
usvi nA (5)
• U is a mn orthogonal matrix: Tm
I
UU .
• V is a nn orthogonal matrix: Tn
I
VV .
The columns of U and V may be chosen so that they
form an orthonormal basis of the column space and row
space, respectively of A. If A has full rank, then its
singular values are all positive, and when they are or-
dered as indicated, then the SVD is unique up to the
signs of the columns of U and V. All of these can be
extended to a general mn complex matrix A. The
decomposition in Eq. (1) implies that

T
TT TT2TE

A
AUSVUSVVSUUSVVS V (6)
since U is orthonormal and
S
is diagonal.
Also because T1 VV, we have

T2
AAV VS
which shows that the columns of V are eigenvectors of
T
A
A. The singular values of A are the square roots of
the corresponding eigenvalues. The SVD is motivated by
the following geometric fact: The image of a unit sphere
under the matrix mn A is a hyper-ellipse as shown in
Figures 1 and 2. Considering each column of V sepa-
rately, the latter is the same as
,1,2,,
iii
vsui nA (7)
Thus, the unit vectors of an orthogonal coordinate sys-
tem


1,, n
vvare mapped under A onto a new
“scaled” orthogonal coordinate system

11
,,
nn
s
usu.
In other words, the unit sphere with respect to the matrix
2-norm (which is a perfectly round sphere in the v-sys-
tem) is transformed to an ellipsoid with semi-axes i
s
.
x
Vx
V Σ U
ΣVx UΣVx
Figure 1. SVD transformation diagram.
Figure 2. Geometrical interpretation of SVD transformation.
Interpretation of full SVD of T
AUSV given
yx

A is as follows,
1) Rotate by T
V
2) Scale along axes by i
s
3) Zero-pad (if mn) or truncate (if mn

) to get
m-vector
4) Rotate (by U)
5)


1xx

A is ellipsoid with principal axes ii
s
u
SVD of matrix mn

A with rank Rank (A) = r is:

T
11
T
1
T
mnmxrrxrrxnn
rr
s
v
uu
s
v

















AUSV
A convenient starting point in the synthesis of SVD is
the construction of its components to validate their
properties. For the sake of presentation let us examine an
image of a tumor brain cancer shown in Figure 3. SVD
of image 3 is analyzed and displayed in Figure 5. It is
worth to mention that the black color is coded as zero,
meanwhile non-black color would appear as gray or
white color. Digitization of a selected position marked
by the curser in the tumor image is shown in Figure 4. It
is worthy to mention that the diagonal egienvalues are
represented in Figure 5 as a white diagonal line with
some zero values in black. Since SVD geometrically
interprets an ellipsoid transformation, then the higher the
eigenvalues, the more of tumor growth is.
4. DYNAMIC TUMOR IDENTIFICATION
In this section consider the following dynamic time-
varying linear system that describes the change in the
invasion of gliomas in white-gray matter as follows,


ttt

xAx (8)
where


tx is the n-dimensional state vector and


A
t
is a non-singular time-varying matrix of mn dimension.
Practically the matrix


tA represents the observed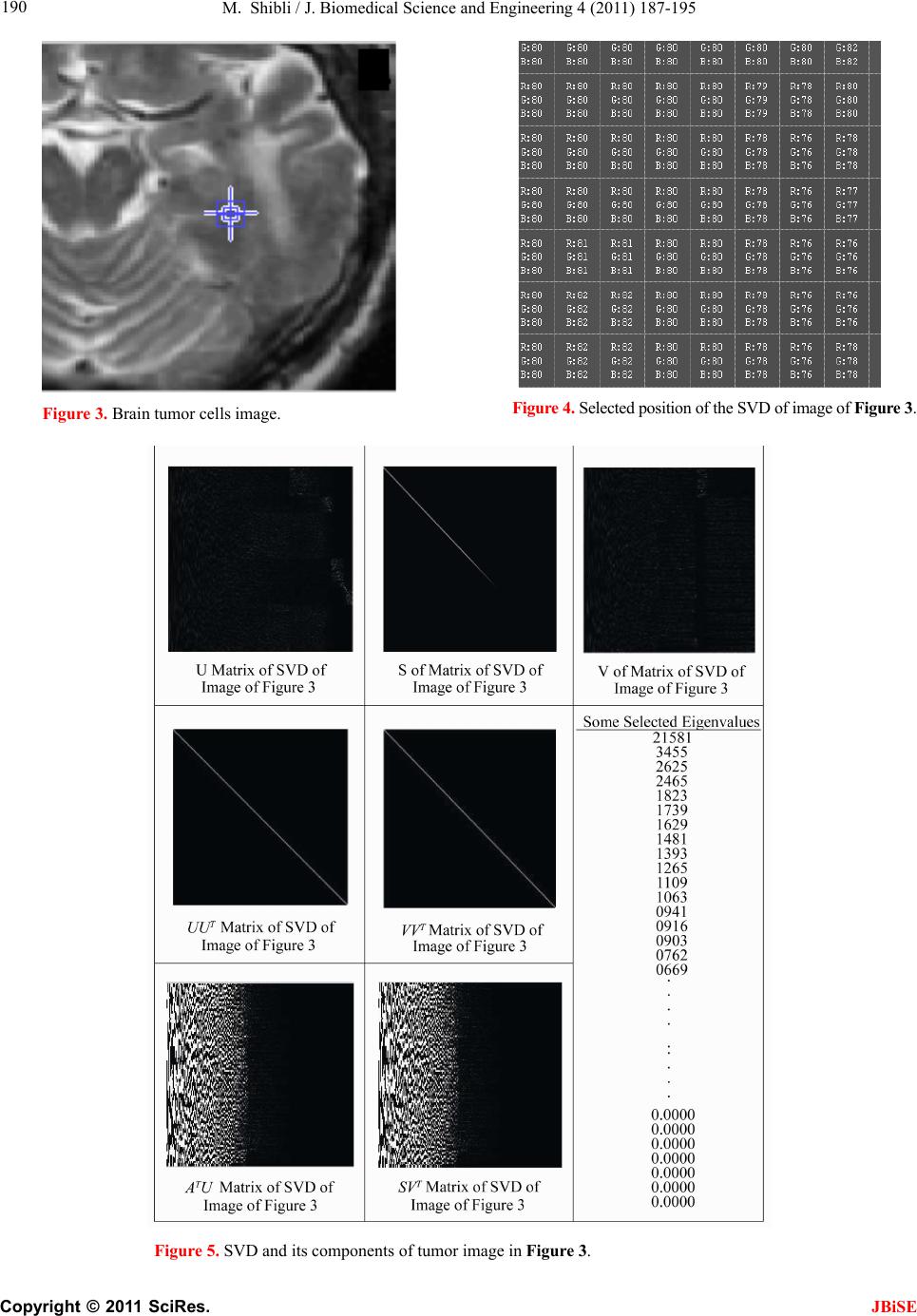

M. Shibli / J. Biomedical Science and Engineering 4 (2011) 187-195
190
Figure 3. Brain tumor cells image.
Figure 4. Selected position of the SVD of image of Figur e 3 .
Figure 5. SVD and its components of tumor image in Figure 3.

M. Shibli / J. Biomedical Science and Engineering 4 (2011) 187-195
191
image matrix of the tumor status taken at time t.
In order to formulate the problem, we assume that
there are two observed images have been recorded at
time 1 t and 2 t, respectively. In the present problem the
objective is to identify the white and gray matter growth
by using the singular value decomposition. By the virtue
of the former dynamics equation, the change in the tu-
mor status can be formulated as:
 

 
212 1 21
tt tttt  

  xx xAAx x (9)
which can be simplified to
 
ttt

xAx
(10)
The last Eq. (10) represents the dynamic image of the
tumor growth. Benefiting from the properties of SVD
yields
 
T
2222
ttttAUSV (11)
 
T
111
1
ttttAUSV (12)
To serve solving the current objective using dynamic
Eq. (10) and by utilizing Eqs. (11) and (12), then the
tumor invasion growth matrix


tA is proportional to
the change in the diagonal matrix change

tS. Which
means that any growth in the white-grey matter image
can be identified by a non-zero diagonal matrix


tS.
Now for the sake of investigating the growth of the
tumor cells by identifying the white-gray matter, two
pairs of images have been examined using SVD tech-
nique. Each pair represents the same patient but with
different times recording as shown in Figures 7-10. The
SVD of each image has been performed. Components of
the image matrix decomposition are displayed in each
figure. Figures 7 and 8 are taken for the same patient but
at different times. Images show a change in the white-
gray matter which indicate there is a tumor cancer
growth growing. This can be validated by checking the
diagonal matrix. It can be seen that each image has its
own unique diagonal eigenvalues. The net change in the
diagonal eigenvalues matrix

tS is computed and
demonstrated in Figure 6. This vertical indicator repre-
sents how high the tumor growth is. Black regions indi-
cate that there is no growth in the tumor cells. Mean-
while, the white region on the vertical indicator implies a
cancer cell growth. This tool is very efficient to track
and identify the region of tumor growth of the white-
gray matter to follow-up the patient status.
5. INVESTIGATING MOUSE MODEL
Animal models of cancer, particularly mouse models of
cancer, are commonly used to study tumor biology and
develop new approaches to conquering human cancer.
Priori research in modeling cancer on laboratory animals,
Figure 6. Tumor growth indicator of the change of the diago-
nal eigenvalue matrix


tS of images in Figure 7-10.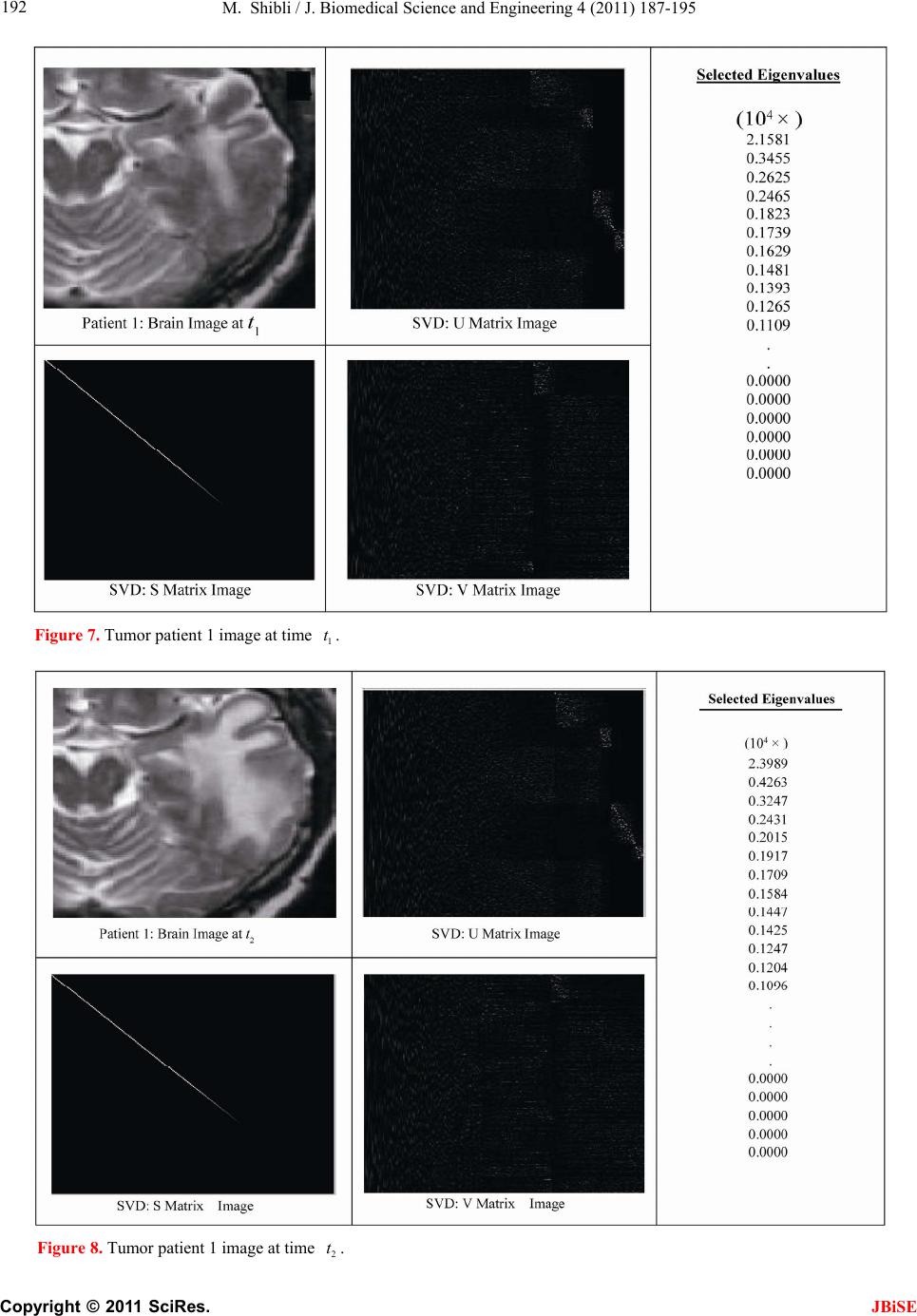

M. Shibli / J. Biomedical Science and Engineering 4 (2011) 187-195
192
Figure 7. Tumor patient 1 image at time 1 t.
Figure 8. Tumor patient 1 image at time 2 t.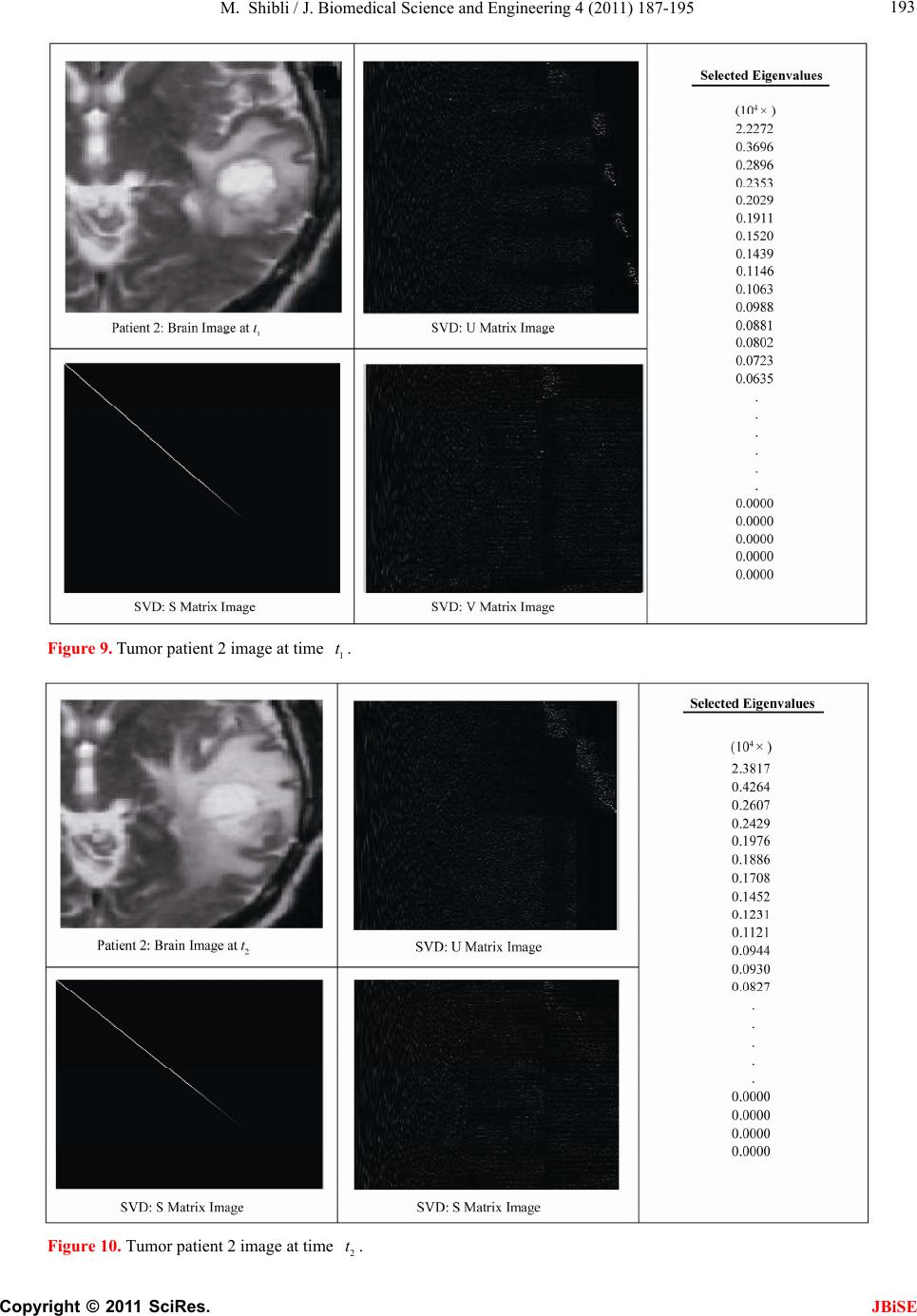

M. Shibli / J. Biomedical Science and Engineering 4 (2011) 187-195
193
Figure 9. Tumor patient 2 image at time 1 t.
Figure 10. Tumor patient 2 image at time 2 t.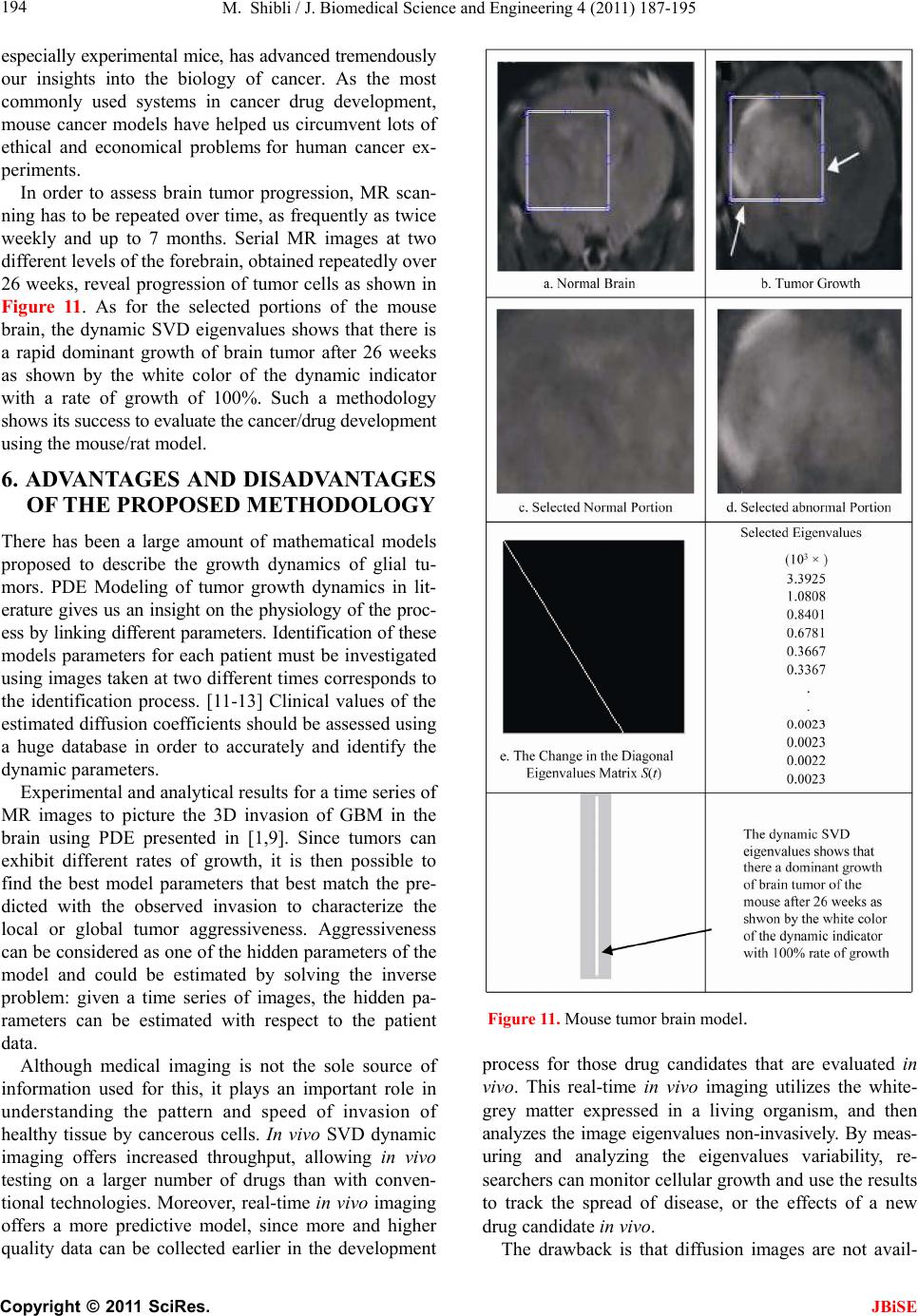

M. Shibli / J. Biomedical Science and Engineering 4 (2011) 187-195
194
especially experimental mice, has advanced tremendously
our insights into the biology of cancer. As the most
commonly used systems in cancer drug development,
mouse cancer models have helped us circumvent lots of
ethical and economical problems for human cancer ex-
periments.
In order to assess brain tumor progression, MR scan-
ning has to be repeated over time, as frequently as twice
weekly and up to 7 months. Serial MR images at two
different levels of the forebrain, obtained repeatedly over
26 weeks, reveal progression of tumor cells as shown in
Figure 11. As for the selected portions of the mouse
brain, the dynamic SVD eigenvalues shows that there is
a rapid dominant growth of brain tumor after 26 weeks
as shown by the white color of the dynamic indicator
with a rate of growth of 100%. Such a methodology
shows its success to evaluate the cancer/drug development
using the mouse/rat model.
6. ADVANTAGES AND DISADVANTAGES
OF THE PROPOSED METHODOLOGY
There has been a large amount of mathematical models
proposed to describe the growth dynamics of glial tu-
mors. PDE Modeling of tumor growth dynamics in lit-
erature gives us an insight on the physiology of the proc-
ess by linking different parameters. Identification of these
models parameters for each patient must be investigated
using images taken at two different times corresponds to
the identification process. [11-13] Clinical values of the
estimated diffusion coefficients should be assessed using
a huge database in order to accurately and identify the
dynamic parameters.
Experimental and analytical results for a time series of
MR images to picture the 3D invasion of GBM in the
brain using PDE presented in [1,9]. Since tumors can
exhibit different rates of growth, it is then possible to
find the best model parameters that best match the pre-
dicted with the observed invasion to characterize the
local or global tumor aggressiveness. Aggressiveness
can be considered as one of the hidden parameters of the
model and could be estimated by solving the inverse
problem: given a time series of images, the hidden pa-
rameters can be estimated with respect to the patient
data.
Although medical imaging is not the sole source of
information used for this, it plays an important role in
understanding the pattern and speed of invasion of
healthy tissue by cancerous cells. In vivo SVD dynamic
imaging offers increased throughput, allowing in vivo
testing on a larger number of drugs than with conven-
tional technologies. Moreover, real-time in vivo imaging
offers a more predictive model, since more and higher
quality data can be collected earlier in the development
Figure 11. Mouse tumor brain model.
process for those drug candidates that are evaluated in
vivo. This real-time in vivo imaging utilizes the white-
grey matter expressed in a living organism, and then
analyzes the image eigenvalues non-invasively. By meas-
uring and analyzing the eigenvalues variability, re-
searchers can monitor cellular growth and use the results
to track the spread of disease, or the effects of a new
drug candidate in vivo.
The drawback is that diffusion images are not avail-

M. Shibli / J. Biomedical Science and Engineering 4 (2011) 187-195
195
able for every patient and existence of the tumor and the
low quality of patient images make it hard to obtain an
accurate white matter segmentation. Additionally, high
resolution MR equipments are required.
7. CONCLUSIONS
This paper presents a novel method to quantify the
growth of tumor invasion in white and grey matter for
gliomas of MR images using SVD. This methodology is
found to be fruitful to detect tumor cancer and follow-up
patient and gives quantitative values about its growth.
Quantification process is formulated based on the image
SVD eigenvalues. Since SVD is interpreted by en ellip-
soid, then the higher the eigenvalues the more of tumor
growth would be. Two pairs of brain images of two pa-
tients have been examined. The brain of each patient has
been imaged twice at different times. By then, SVD of
each image has been processed.
It is found that each image is characterized by unique
diagonal egienvalues matrix. The tumor cancer growth is
identified by these egienvalues. Considering the differ-
ence of the two corresponding matrices egienvalues will
identify the growth rate. Based on this analysis an effi-
cient white-black indicator is constructed. Black indica-
tor means that there is no cancer growth. On the contrary,
white indicator shows a growth in the tumor abnormal
cells. Simulation results verify the SVD image process-
ing approach. The advantage of such an approach is that
for each patient, a dynamic indicator can constructed to
evaluate his tumor growth at any time compared to a
former one and follow-up his/her treatment.
This approach is advantageous compared to PDE
models, since clinical values of the estimated diffusion
coefficients should be assessed using a large database in
order to accurately and identify the dynamics parameters.
On the contrast, real-time SVD in vivo imaging offers a
more predictive model, since more and higher quality
data can be collected earlier in the development process
for those drug candidates that are evaluated in vivo. By
measuring and analyzing the eigenvalues variability,
researchers can monitor cellular growth and use the re-
sults to track the spread of disease, or the effects of a
new drug candidate non-invasively.
REFERENCES
[1] Konukoglu, E., Clatz, O., Bondiau, P.Y., Sermesant, M.,
Delingette, H. and Ayache, N. (2007) Towards an identi-
fication of tumor growth parameters from time series of
images. Medical Image Computing and Computer-Assisted
Intervention—MICCAI 2007 Lecture Notes in Computer
Science, 4791, 549-556.
doi:10.1007/978-3-540-75757-3_67
[2] Nugroho, H.A., Ihtatho, D. and Nugroho, H. (2008) Con-
trast enhancement for liver tumor identification. The
MIDAS Journal—Grand Challenge Liver Tumor Seg-
mentation (MICCAI Workshop), Private Issue, Kitware
Inc., USA.
[3] Ishizawa, T., Fukushima, N., Shibahara, J., Masuda, K.,
Tamura, S., Aoki, T., Hasegawa, K., Beck, Y., Fukayama,
M. and Kokudo, N. (2009) Real-time identification of
liver cancers by using indocyanine green fluorescent im-
aging. Cancer, 115, 2491-2504.
doi:10.1002/cncr.24291
[4] Chin, K.M., Wessler, B., Chew, P. and Lau, J. (2006)
Genetic tests for cancer. Agency for Healthcare Research
and Quality (AHRQ). Technology Assessment.
http://www.ahrq.gov/clinic/ta/gentests/gentests.pdf
[5] Villers, A., Puech, P., Leroy, X., Biserte, J., Fantoni, J.C.
and Lemaitre, L. (2007) Dynamic contrast-enhanced MRI
for preoperative identification of localised prostate can-
cer. European Urology Supplements, 6, 525-532.
doi:10.1016/j.eursup.2007.01.024
[6] Klema, V.C. and Laub, A.J. (1980) The singular value
decomposition: its computation and some applications,”
IEEE Transactions on Automatic Control, 25, 164-176.
doi:10.1109/TAC.1980.1102314
[7] Ashino, R., Morimoto, A., Nagase, M. and Vaillancourt,
R. (2003) Comparing multiresolution SVD with other
methods for image compression. Proceedings of the 4th
International ISAAC Congress, York University, Toronto,
11-16 August 2003, 457-470.
[8] Joro, R., Lääperi, A.L., Soimakallio, S., Järvenpää, R.,
Kuukasjärvi, T., Toivonen, T., Saaristo, R. and Dastidar,
P. (2008) Dynamic infrared imaging in identification of
breast cancer tissue with combined image processing and
frequency analysis. Journal of Medical Engineering &
Technology, 32, 325-335.
doi:10.1080/03091900701541240
[9] Clatz, O., Sermesant, M., Bondiau, P., Delingette, H.,
Warfield, S., Malandain, G. and Ayache, N. (2005) Re-
alistic simulation of the 3D growth of brain tumors in
MR images coupling diffusion with biomechanical de-
formation. IEEE Transactions on Medical Imaging, 24,
1334-1346. doi:10.1109/TMI.2005.857217
[10] Konukoglu, E., Sermesant, M., Clatz, O., Peyrat, J.M.,
Delingette, H. and Ayache, N. (2007) A recursive ani-
sotropic fast marching approach to reaction diffusion
equation: Application to tumor growth modeling. Infor-
mation Processing in Medical Imaging, 20, 687-699.
doi:10.1007/978-3-540-73273-0_57
[11] Kirschner, D. (2009) On the global dynamics of a model
for tumor immunotherapy. Mathematical Biosciences
and Engineering, 6, 573-583.
doi:10.3934/mbe.2009.6.573
[12] Ledzewicz, U. (2005) Optimal control for a system mo-
delling tumor anti-angiogenesis. ACSE 05 Conference,
CICC, Cairo, 19-21 December 2005, 147-152.
[13] Ghaffari, A. and Nasserifar, N. (2009) Mathematical
modeling and lyapunov-based drug administration in
cancer chemotherapy. Journal of Electrical & Electronic
Engineering, 5, 151-158.