Circuits and Systems
Vol.07 No.10(2016), Article ID:70087,11 pages
10.4236/cs.2016.710281
FPGA-Based Stream Processing for Frequent Itemset Mining with Incremental Multiple Hashes
Kasho Yamamoto, Masayuki Ikebe, Tetsuya Asai, Masato Motomura
Graduate School of IST, Hokkaido University, Sapporo, Japan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 April 2016; accepted 10 May 2016; published 25 August 2016
ABSTRACT
With the advent of the IoT era, the amount of real-time data that is processed in data centers has increased explosively. As a result, stream mining, extracting useful knowledge from a huge amount of data in real time, is attracting more and more attention. It is said, however, that real- time stream processing will become more difficult in the near future, because the performance of processing applications continues to increase at a rate of 10% - 15% each year, while the amount of data to be processed is increasing exponentially. In this study, we focused on identifying a promising stream mining algorithm, specifically a Frequent Itemset Mining (FIsM) algorithm, then we improved its performance using an FPGA. FIsM algorithms are important and are basic data- mining techniques used to discover association rules from transactional databases. We improved on an approximate FIsM algorithm proposed recently so that it would fit onto hardware architecture efficiently. We then ran experiments on an FPGA. As a result, we have been able to achieve a speed 400% faster than the original algorithm implemented on a CPU. Moreover, our FPGA prototype showed a 20 times speed improvement compared to the CPU version.
Keywords:
Data Mining, Frequent Itemset Mining, FPGA, Stream Processing

1. Introduction
Frequent Itemset Mining (FIsM) is an important and fundamental problem in data mining with regards to association and correlation. FIsM finds frequent itemsets by counting the occurrence of subgroups called itemsets in a transactional database. It is possible to know the relationship between items from frequent itemsets because items contained in frequent itemsets have a high probability of occurring at the same time. The knowledge gained from this technique is widely used in data analytics, such as in the analysis of sensor networks, network traffic, stock markets, and fraud detection.
There is a similar process, Frequent Item Mining (FIM), which is used to discover frequently appearing items in a database. Though the processes sound similar, FIsM is a much more difficult problem compared to FIM because of combinatorial itemset explosion.
In 1994, Agrawal proposed the first Apriori algorithm [1] for FIsM, based on a breadth-first search. Later, a depth-first algorithm called FP-Growth [2] was proposed by Han in 2000. Studies following these works have mainly focused on obtaining higher speeds and reducing memory usage. However, because of the explosive increase in data, a method is needed that can process huge amounts data in real time. Therefore, algorithms that find frequent itemsets in stream data in real time, i.e., stream mining, have been studied extensively.
Since stream data refers to large amounts of data coming in continuously, it is unrealistic to keep all data in main memory. Therefore, the algorithm is not allowed to scan the database multiple times, this memory capacity limitation prevents the method from accurately counting the number of occurrences of all itemsets. For this reason, a single-scan approximation algorithm has been proposed. For example, lossy counting [3] separates transactions into batches and eliminates infrequent itemsets at the end of each batch. The drawback of this algorithm is that a sudden burst of stream data can produce a memory overflow. In contrast, the space saving [4] and Skip LC-SS algorithms [5] address this memory overflow problem by fixing the number of stored itemsets. Unfortunately, this process requires substantial memory access and tends to produce memory access bottlenecks during CPU processing. To address this problem, there has been a substantial amount of research using FPGAs.
In the FPGA implementation of the FIM item-processing algorithm, Teubner proposed the use of a space saving algorithm [6] . Because there is no need to consider the exponential increase in possible combinations, the proposed implementation was able to take advantage of parallelism by using registers. In the implementation of the off-line FIsM algorithm, Baker et al. [7] proposed the first Apriori architecture. Since then, substantial research has been done. However, when implementing FIsM, which handles stream data using an FPGA, it is difficult to handle the exponentially increasing amount of itemsets. There are multiple methods, both based on the proposed algorithm of Liu et al. and a method using a tree proposed by Lazaro. However, they avoid combinatorial explosion by limiting the types of items, as such their application range is limited. Furthermore, HW studies evaluating their accuracy have not yet been presented. In this study, we propose a new hardware-friendly algorithm, based on the Skip LC-SS algorithm. We also consider hardware architecture capable of processing various kinds of data.
Our contributions in this paper are as follows:
We propose a faster and memory-efficient algorithm for hardware based on Skip LC-SS.
We explain a method to store itemset on small BRAMs without tree structure.
We verify the improvement of performance with standard evaluation tool that is capable of evaluating various FIsM.
This paper is organized as follows. The algorithm, which is the base of our algorithm, is described in Section 2. The discussion in Section 3 gives the hardware that is designed to work with our proposed algorithm. Experimental and evaluation results are described in Section 4. We then summarize our research in Section 5.
2. Skip LC-SS Algorithm
2.1. Background
In Figure 1, we explain the notation and terminology used in this paper. Let I = a, b, c,... be a set of items. An itemset is composed of a subset of I, excluding the empty set. S, a transactional data stream, is continuous data containing transactions T1, T2 ...Tn, where Ti is the transaction that arrives at time I and N is any huge number. Let e be an entry, and the support of e, shown by sup(e), is the number of transactions that include e in the stream S.
Given a minimal support threshold, σ satisfying ∈ (0, 1). If sup(e) ≥ σN, e is frequent itemset. In this algorithm, the counter called frequent counter for each mining target is held.
An entry table D is a table used to store the entries. K is the maximum number that can be held in table D. |D| denotes the number of entries in D. The minimum entry is entry e with a minimum of the frequent count in D. Given a minimal support threshold σ (0 < ∆/N < σ), the Skip LC-SS algorithm can be used to output all the items in set e such that sup(e) ≥ σN (no false negative), where ∆ is a lower limit such that the recall is guaranteed to be 1.
Figure 1. Processing example of T1.
2.2. Skip LC-SS Algorithm
The Skip LC-SS algorithm was proposed by Yamamoto et al. in 2014. It can be extended to be used with the FIsM algorithm that corresponds to stream data by integrating it with Lossy Counting algorithm and space saving algorithm. It used the features of the Space Saving Algorithm to fix the number of entries to be saved. The processing unit in the transaction was the Lossy Counting Algorithm (LC-SS), in order to speed up the algorithm, some approximation process (skip) was added. As described above, this algorithm fixes the number of stored entries. Given a constant k, entry table D, and data stream containing plural transactions, the LC- SS Algorithm operates in the following manner in accordance with the state of the entry table. In this case, c(ei) is the number of occurrences of the i-th itemset ei and m is an entry with the minimum number of occurrences in the entry table.
• Case 1: |D| < K
1) if < ei, c(ei) >  D, increment c(ei) by one.
D, increment c(ei) by one.
2) else, store the new itemset
3) if |D| < K, set error count(∆) to one.
4) after cheking all itemset, process next transaction.
We show the method used to process T1 in Figure 1 (Case 1). At this time, since |D| = 0 and K = 7, the process shown in Case 1 is followed. In the initial state, Delta = 0. First, enumerate itemsets that could be contained in T1. Then, confirm whether each itemset appears in the entry table. Because T1 is the first transaction, the entry table is empty. Therefore, all itemset are stored. However, if the number of itemsets exceeds K, the method shown in Case 2 is used. In this case, after all itemsets are checked, error count (∆) is incremented by one because the entry table has been filled. At this point the next transaction is processed.
• Case 2 : |D| = K
1) if
2) else store ei as a candidate.
3) after checking all itemset, replace the minimal entry
4) update error count (∆) to c(m).
5) process next transaction.
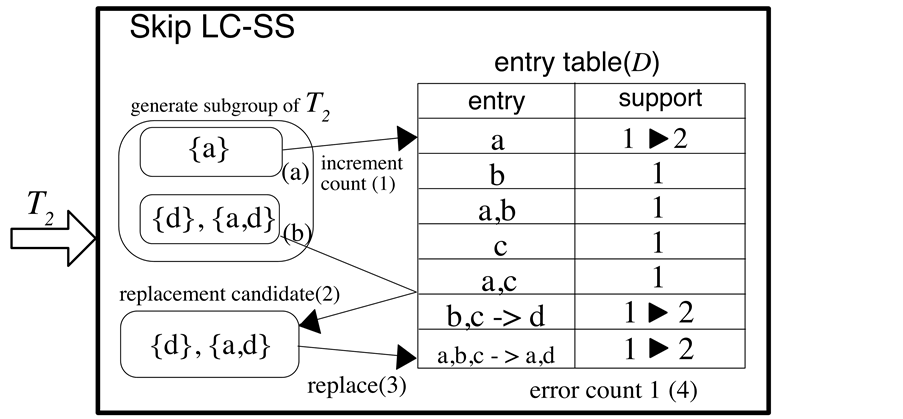
The processing of T2 is shown in Figure 2 (Case 2). Here {a} is already stored in the entry table, and its frequency is incremented by one. Because {d} and {a,d} are not registered in the entry table, a replacement candidate is registered. Then, an arbitrarily selected entry among the entries with the lowest frequency in the table is replaced with the replacement candidate. Afterwards, error count (∆) is updated. The minimum value of the entry table is one, so in this case the error count remains at one.
Figure 2. Processing example of T2.
In this algorithm, memory consumption is kept constant. However due to the use of the minimum value search and replacement, processing time is negatively affected. Thus, Yamamoto et al. introduced an approximation process to simplify (skip) the processing of replacement and large transactions, which cause a reduction in processing speed. The methods were termed the t2-skip and r-skip. If 2|Ti|−1 > k, the entry table frequency and error counts are incremented by one. Afterwards, the transaction is completed (t2-skip). Thus, it is possible to efficiently process a huge amount of transactions without causing significant performance degradation.
r-skip is an approximation process, but it is omitted because it is not used, as will be described later. Finally, in order to prevent the accuracy degradation due to r-skip and t2 skip, Yamamoto et al. proposed stream reduction. Stream reduction is a pre-processing method performed on the input transactions. The method executes FIM on transactions, and compares the frequency of items included in the incoming transaction with ∆. Items whose frequency is lower than ∆ are then removed from the transaction as an infrequent itemset. This enables the method to perform frequent itemset mining from relatively frequent items. Therefore, Skip LC-SS retains accuracy even when used with r-skip and t2-skip techniques to accelerate the processing.
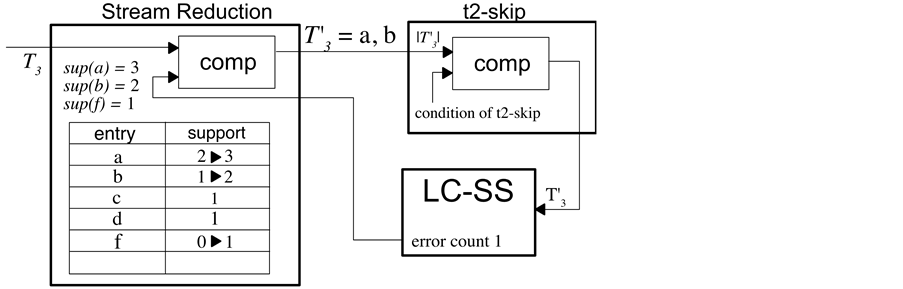
Figure 3 shows an example of stream reduction, we apply stream reduction from this example. When the input transaction T3 = a, b, f is counted, occurrences of each item is (3, 2, 1). However, after processing transaction t2, ∆ = 1. Because the frequency of item f is less than delta, transaction T3’ is to be processed at a later stage than a and b. Afterwards, for this transaction, it is determined whether to execute the t2-skip. Because 22-1 < 7 (the condition of the t2-skip), this transaction is processed in LC-SS part of the algorithm (details omitted).
3. Hardware Design
The maximum point of FIsM on hardware is considered configuring the entry table. In this study, we used a hash table to confirm whether itemsets were registered in the entry table for a small number of memory accesses. We list the following three issues when considering the hardware used to implement this algorithm.
1) Limitation of the amount of BRAM. (3.1)
Because the size of the BRAM is much smaller than the amount of memory that could be used by the server, the number of itemsets in the entry table is limited. This limitation lowered practicality for a huge data set. In custom chips, area is an issue.
2) Searching the minimal frequent count of the entry table is not suitable for hardware. (3.2)
The process of replacement requires that the minimal frequent count is found. However, sorting is not a problem well suited for FPGAs.
3) The lack of parallelism of the original algorithm. (3.3)
In the Skip LC-SS Algorithm, it is impossible to perform a count-up and replace at the same time because sequential processing is assumed.
Figure 3. Stream reduction and its example.
3.1. Incremental Hash
In the Skip LC-SS algorithm, it is necessary to perform many processes, such as registering an itemset, confirming a registered itemset, counting up, and conducting sorting and replacement in the entry table for each transaction. Furthermore, these processes change depending on the state of the table. Therefore, frequent memory access becomes a bottleneck when DRAM is used instead of BRAM because of its latency. Considering the latency of reference itemsets, our approach is to configure the hash table using BRAM. This allows us to confirm the existence of itemsets at high speed with low latency. However, the size of BRAM is too small as mentioned above. Therefore, the itemset cannot be stored as string as in other software implementation. It is necessary to use a compact data structure for an efficient implementation with the hardware.
Figure 4 shows the solution we propose. In the conventional hashing method (a), itemsets are stored and searched according to the value output from a hash function after an itemset (key) string was inserted. However, it is necessary to save the original itemset to confirm whether the hashed itemset and stored itemset are the same because hash function sometimes output the same value for different itemsets (collision). However, itemset scan not directly be stored in BRAM due to capacity limitations.
Therefore, to obtain a more efficient data structure, we considered that not only can the bit string indicatean itemset, its address is stored in accordance with the hash value obtained by hashing the itemset and is an unique value. Specifically, the itemset key contains n + 1 items (length n + 1), which consists of the new item (length 1) and the initial itemset address containing n items. Based on this idea, we propose a hash table to enable efficient searching and memory saving.
Our proposed method is shown in Figure 4(b). For an itemset of length 1, the method is the same as conventional methods. However, for an itemset of length greater than two (in our example itemset
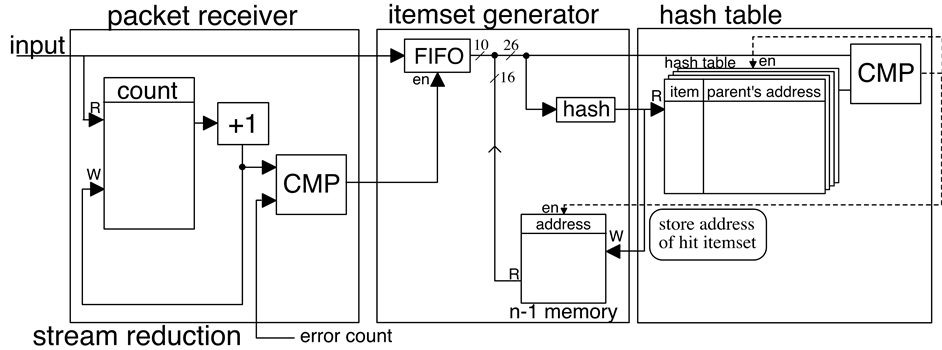
Figure 5 shows a simplified block diagram of the stream reduction, itemset generator and hashtable. The process is as follows.
Figure 4. (a) Conventional hashing and (b) proposed hash our methods.
Figure 5. Hardware architecture of itemset generator and hash table.
Figure 6 shows image of our sort. If itemset <a, b> hit in hash table, the address and hit flag are transferred to sort function. Then, we obtain its counter address (2) from entry table and get frequency (value 1) and top address among group, which has same frequency (address 01). Afterwards, we swap entry <a, b> and < b>. Frequency of <a, b> is incremented by one, and check whether there is counter which has the same value. If we have already had the same counter, the counter address of itemset <a, b> is changed to 1. Otherwise, we create new counter.
3.3. Batch Replace
In this section, we propose a method to replace the Skip LC-SS Algorithm in the proposed hardware. In this al-
Figure 6.The image of sorting.
gorithm, we assume that the hardware allows us to count and sort at the same time. However, these two pro- cesses cannot be executed simultaneously with the replacement process. Therefore, it is necessary to stop these processes and switch processing actions for each transaction.
Instead of processing replacements during each transaction, we propose a method for batch processing a plurality of transactions. We then explore frequent itemsets among the replacement candidates generated from each transaction using counting. Possible replacements for the frequent itemset groups and the current entry table are combined at the end of the batch. Here, the problem is the proportion of itemsets that are not hit and the itemsets that hit the entry table. If the number of itemsets that do not hit is large, a bottleneck appears replacement candidates for the frequent itemsets are still being found. Therefore, replacement candidates generated through this process are generally itemsets whose length is the same as the frequent itemset in the entry table plus one, because they are likely to be frequent. That is, we will explore the frequent itemsets from the itemsets that were not found in the hash table. A search of the itemset that contains an itemset that was not hit in the hash table is terminated.
Figure 7 (upper) shows the original Skip LC-SS chart and our algorithm chart. Then the lower side of Figure 7 shows our proposed hardware architecture. Hash table and sorting is mentioned above. Itemsets that were not hits in the hash table are sent to the FIM module, and then found through frequent itemset mining. After all transactions of process in batch are processed and combined in the entry table and replacement candidates are found, we process the next batch. Almost all processes in this algorithm can be processed in parallel, except the process of coupling the hash table. Therefore, we expect further speed improvements.
4. Evaluation
4.1. Dataset & Environment
In order to obtain reliable data, we created evaluation data using a Synthetic Data Generator widely used to evaluate the performance of FIsM by the IBM Almaden Quest research group. This dataset is generated using the following parameters: “T” is the average number of items included in the transactions, “I” is the average length of the frequent itemset, “D” is the number of transactions included in the database, and “N” is the number of types of items included in the database. We use a label “TxIyDz (T = x, I = y, D = z)” to denote the characteristics of a dataset. Thereafter, in order to reveal the various characteristics of our algorithm, we conducted experiments by incrementally changing each parameter. Finally, to evaluate the algorithm more realistically, we evaluated it using a dataset that contained retail market basket data created by Tom Brijs. Most experimental results were obtained using an Intel Xeon E5-1620. Experiment 5-3 was evaluated using a Mac Pro with Mac OS 10.6, 3.33 GHz, 16 GB. Hardware (HW) results were evaluated based on the RTL simulation with 156 MHz. Target device is ZC706 and the resource usage is shown in Table 1 and Table 2.
4.2. Basic Properties of the Improved Algorithm
“Precision” is a metric indicating how often the frequent itemsets identified by the algorithm are truly frequent itemsets. ‘Recall’ is a metric indicating how often the algorithm identifies the real frequent itemsets.
These metrics indicate the accuracy of the FIsM results. The depth of the hash table is 12-bit and it has an associativity of 16. The size of the entry table is 10K. The size of the hash table and the entry table is the same.
Figure 7.(upper) flow of original and improved algorithm; (lower) hardware architecture of batch replacement.
Table 1. Parameter summary.
Table 2. FPGA chip resource consumption and clock freq.
Figure 8 compares the characteristics of FIsM algorithms (execution speed, precision, and recall). Because of the presence of the replacement batch size parameter in our improved version of the Skip LC-SS algorithm, we first evaluated the original and improved Skip LC-SS algorithms in SW, and then evaluated the improved algorithm in HW. In the later comparison, we set the T10I4D100K parameter (used widely in various studies) and varied the batch size. As shown in Figure 8(a), the improved algorithm is faster in both SW and HW than the original Skip LC-SS algorithm. Here, a large difference between the Original Skip LC-SS and improved algorithm is not seen because size of dataset is small. The execution time in the HW implementation is an average of 20 times shorter than that of the SW implementations. From this, we confirm that using parallel processing with this method is very effective, as said in Section 3.3. This is due to the newly implemented use of batch replacement. From Table 3, we see that frequent itemsets are successfully found with good precision and recall.


Figure 8.Execution time with respect to batch size, database items, and average transaction length.
Table 3. HW Algorithm precision, recall (T10I4D100K).
Figure 8(b) and Figure 8(c), shows the experimental results after varying the parameters of the aforementioned datasets. Figure 8(c), is the result of varying the average number of items in transactions included in the data set (T) based on the TxI4D10K parameter. As transaction length increases, processing time also increases because the number of generated itemsets increases as O(2L). In addition, in SW and HW, processing speed remains at a realistic value, while itemsets increase explosively due to the exponential increase in combinations. This is because an increase in T does not lead to an increase in the processing target due to the stream summary and efficient search methods.
Figure 8(b) gives the experimental results while changing the type of items included in the data set (N). It can be seen that as more types of items are included in the dataset, the execution time decreases. Increases in the types of item leads to the increase in infrequent items because the other parameters do not change. Thus, increasing the number of infrequent items results in a higher number of items removed from the transactions. Therefore, the processing speed of both SW and HW increased in the same way. Since the processing time is independent of the types of items, the more items the Stream Reduction prunes, the shorter the execution time.
4.3. Real Data
Figure 9 gives the evaluation results of the algorithm using the dataset based on log data of actual purchasing

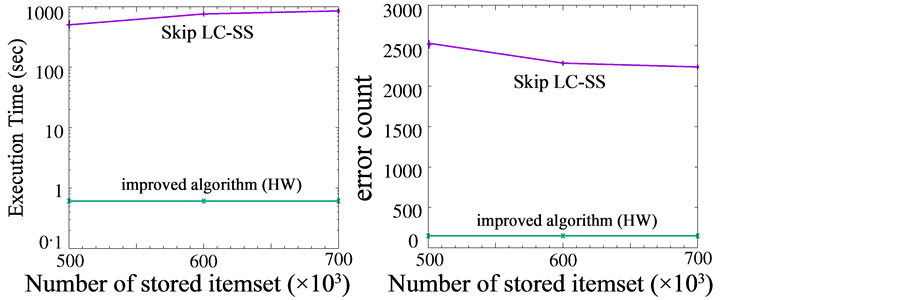
Figure 9.Execution time and error count of retail and web log items in set e such that sup(e) ≥ σN (no false negative), where ∆ is a lower limit such that the recall is guaranteed to be 1. (a) dataset: retail; (b) dataset: web_log.
information and a web click stream. The retail data consists of 88,162 transactions and 16,470 items; the web- log data stream consists of 19,466 transactions and 9961 items. As mentioned above, SW evaluation data is obtained from the original skip LC-SS paper by Yamamoto using the same dataset. The limit of the stored itemsets is 500 K, 600 K, and 700 K respectively. The configuration of the HW was the same as in the previous section (bucket size 10 K). As a result, despite the much smaller bucket size compared to the original algorithm, processing speed was 100 times faster and the error count necessary to guarantee minimum support was 100 times smaller. By introducing a batch process, we achieved a more efficient algorithm. Since the original algorithm executes the approximation process repeatedly on huge transactions, memory efficiency was reduced. However, the proposed algorithm uses memory more efficiently because it selects potential frequent itemsets and replaces them with frequent replacement candidates. Even in realistic datasets, this algorithm works well.
5. Conclusion
In this paper, we propose a hardware-friendly algorithm to increase the use of parallelism in FIsM processes in the original Skip LC-SS algorithm. By identifying the bottleneck in the original algorithm, we were able to successfully introduce a more efficient replacement process using our batch-replacement concept. The proposed algorithm also maintains an error count in order to guarantee minimum necessary support, which in turn makes it possible to keep the amount of memory consumption low. As a result, we achieved a 100 times faster and more memory-efficient algorithm. Because our algorithm limits the replacement target and prunes itemsets, except the itemset whose length is the length of the current frequent itemset plus one, it is possible that a frequent itemset that contains many items may be missed if the batch interval is not appropriate. In the future, we will improve our work by adding the capability to dynamically change the batch interval. This is aimed at producing a more accurate, fast, and hardware-friendly FIsM algorithm and a hardware implementation.
References
- 1. Agrawal, R. and Srikant, R. (1994) Fast Algorithms for Mining Association Rules in Large Databases. Proceedings of the 20th International Conference on Very Large Data Bases, Santiago de Chile, 12-15 September 1994, 487-499.
- 2. Han, J., Pei, H. and Yin, Y. (2000) Mining Frequent Patterns without Candidate Generation. Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data (SIGMOD’00), Dallas, 15-18 May 2000, 1-12.
http://dx.doi.org/10.1145/342009.335372 - 3. Metwally, A., Agrawal, D. and El Abbadi, A. (2005) Efficient Computation of Frequent and Top-k Elements in Data Streams. Proceedings of 10th International Conference on Database Theory (ICDT’05), Edinburgh, 5-7 January 2005, 398-412.
http://dx.doi.org/10.1007/978-3-540-30570-5_27 - 4. Manku, G.S. and Motwani, R. (2002) Approximate Frequent Counts over Data Streams. Proceedings of the 28th International Conference on Very Large Data Bases (VLDB’02), Hong Kong, 20-23 August 2002, 346-357.
- 5. Yamamoto, Y., Iwanuma, K. and Fukuda, S. (2014) Resource-Oriented Approximation for Frequent Itemset Mining from Bursty Data Streams. Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data (SIGMOD’14), Snowbird, 22-27 June 2014, 205-216.
http://dx.doi.org/10.1145/2588555.2612171 - 6. Teubner, J., Mueller, R. and Alonso, G. (2010) FPGA Acceleration for the Frequent Item Problem. Proceedings of the IEEE 26th International Conference on Data Engineering (ICDE), Long Beach, 1-6 March 2010, 669-680.
http://dx.doi.org/10.1109/icde.2010.5447856 - 7. Baker, Z. and Prasanna, V. (2005) Efficient Hardware Data Mining with the Apriori Algorithm on FPGAs. Proceedings of the 13th Annual IEEE Symposium on Field Programmable Custom Computing Machines (FCCM’05), 18-20 April 2005, 3-12.
http://dx.doi.org/10.1109/fccm.2005.31