Journal of Environmental Protection, 2011, 2, 109-114
doi:10.4236/jep.2011.21012 Published Online March 2011 (http://www.SciRP.org/journal/jep)
Using MCMC Probit Model to Value Coastal
Beach Quality Improvement
Zuozhi Li, Erda Wang, Jingqin Su, Yang Yu
School of Management, Dalian University of Technology, Dalian, China.
Received revised October 18th, 2010; revised November 25th, 2010; accepted December 29th, 2010.
ABSTRACT
Dichotomous choice elicitation technique of contingent valuation method is broadly used in the research fields of envi-
ronmental resource and recreational activity management. The binary choice type of questions are generally analyzed
by using Logit or Probit probability distribution models in which a common analysis procedure is to apply MLE for
estimating variable parameters before calculating the respondents’ willingness to pay. In this paper, a MCMC Gibbs
sampling Probit model is adopted to maintain the three advantages it has in dealing with heteroscedasticity, high di-
mension numerical integral and sample size restriction problems. The results revealed that the MCMC model and MLE
Probit model are strikingly consistent, which suggests that the former is much simple and reliable estimation method. At
the same time, the empirically based existence value estimation of coastal beach quality improvement in Dalian, China
is RMBҰ168 per person.
Keywords: Value of Coastal Beach Quality, Markov Chain Monte Carlo (MCMC), Probit Model
1. Introduction
Contingent valuation technique is commonly used in
environmental resource management fields, and monetized
benefit measurement for improvements of environmental
goods. Abundant research in beach nourishment has been
conducted by applied economists [1-4]. In this paper, we
are primarily concerned over the subject of coastal beach
quality improvement with a particular emphasis on the
relationship between tourism beach nourishment and
tourists’ socioeconomic characteristics and the nature of
their tourism activities as well. Beach conditions such as
slope, width, mud, debris, congestion etc. are easily ob-
servable and perceptively recognized by the tourists
through photos presented to them. Tourists’ responses to
the improved situation of coastal tourism resource quality
is depended on a sequence of bidding value data to let
respondent decide “Yes” or “No” regarding acceptance
or rejection in an empirical survey. The type of binary
dependent variable model in the empirical study can be
estimated utilizing Logit or Probit probability distribu-
tion which is firstly explored by Bishop and Heberlein
(1979) with dichotomous choice (DC) elicitation model
of CVM [5], which is called single-bounded DC.
The theoretical base of this method used in consumer
welfare measurement is analyzed by Hanemann (1984)
using Random Utility Maximization (RUM) [6]. With
the support of the US Department of Commerce’s Na-
tional Oceanic and Atmospheric Administration (NOAA)
[7], RUM based utility difference DC model has been
widely accepted and broadly extended. Traditionally,
parameterized method of OLS or MLE is used, but it
requires satisfying with homoscedastic assumption in
order to be able to carry out a regression procedure in
OLS, as well as a high dimension numerical integral
which sometimes causes difficulty in solving consumer
surplus based on MLE. Therefore, in this paper, we try to
examine the performance of the non-parametric kernel
heteroscedastic MCMC method by comparing its results
against those generated by MLE in order to reveal the
robustness of MCMC Gibbs sampling method.
2. Probit Regression Models
2.1. Heteroscedastic Regression Model
Bayesian treatment of the independent student t linear
model, in which, variances of random error are embodied
in heteroscedastic characteristics broken through the tra-
ditional model to ensure a better statistical fitness (Ge-
weke, 1993) [8]. The useful model is
Funding through the National Natural Science Foundation of China
(NNSFC) with Approval No 70871014

Using MCMC Probit Model to Value Coastal Beach Quality Improvement 110


2
,0, 1,
ii iii
yNi  

 x 

,n
(1)
Or






2
1
11
1
1
1
,var,diag, ,
,,
,,
,,
,,
n
nn
nk n
n
n
yy






 













yX
y
Xxx
 


(2)
And the likelihood function is



2
2
12 2
1 1
,,;, 2
exp 2
nn
nn
iii
i i
L
y




 




 






yX
x

i








According to (1), there exist three hyper-parameters,
and then the prior density is

123
,,   

 
Bayesian Markov chain Monte Carlo (MCMC) method
is a comprehensive approach to solve high dimension
numerical integral, because the analytical solution of
exact posterior moments cannot be done, in the paper, the
Gibbs sampler is used to draw a sequence of data. To use
MCMC, the key point is to find the conditional posterior
distributions. Hyper-parameter vector ω is not finally
focused on, and it can be transformed into a single hy-
per-parameter v to assigns an independent


2vv

prior distribution to i

terms. Furthermore, the jth
drawing data set is based on
 

,, ,v 



j
jjjj


.
In his study, the conditional posterior distributions are

1
12-1 12-1
1
212-1
,,N 







 
 

 
 






X
XGTGXyGTg
XX GTG

(3)

 
22 2
1
,
n
ii
i
u  






n
(4)

 
22 2
,
ii
uv v 






1 (5)
2.2. Probit Parameter Method
Probit model is one of binary choice probability distribu-
tion models, which is usually used to solve dichotomous
choice models of contingent valuation method (CVM) in
valuing environmental resource or leisure activities. For
binary choice model, given sampling from i = 1 to n, the
explicit dependent variable is evaluated “0” or “1” as zi
in (6), which is representing the relationship between
implicit dependent variable of continuous distribution as
yi in (6) and explanation variables. Its basic format is as
(6).
0if0
1if0
i
i
i
y
zy



 (6)
In benefit measurement for improvements of tourism
goods, tourists are asked information of willingness to
pay (WTP) for environment or policy change. The WTP
is a bidding value (explanation variable BID in this pa-
per), furthermore, consumer surplus or environmental
improvement value is measured through mean or median
of WTP probability distribution after estimating parame-
ters mentioned β above. Based on the utility difference
model by Hanemann (1984), the implicit dependent va-
riable yi explained with a vector of independent variables
xi can be considered as the utility difference, and his
mentioned utility difference model is like (1) [6]. Ac-
cording to his RUM assumption, given bidding value B,
there is the probability expression as (7).



 


"Yes" ii i PPBWTPPyF   y (7)
Traditional probability distribution of random error is
paid attention to Logit or Probit model [5,6]. In Probit
model, error accords with 0

 and standard
Normal distribution, whose cumulative density function
(CDF) is as (8).
21
 





"Yes" 1
ii
PPzWTP y (8)
Integrated (7) with (8), WTP’s probability density
function (PDF) and CDF could be written as Equation (9)
and (10).
 



12 exp2
x
fx 


 


XX  (9)





2
1,1, ,
112exp2
i
Pz inxx
td 

 
 
X

t
(10)
Through MLE function (11), coefficient parameters β
can be estimated.
  

0
1n1n11n 1
n
ii
i
Lz xzx







(11)
2.3. MCMC Probit Regression Model
In Probit model, i

is distributed as standard normal
distribution, and so in Gibbs sampling, a sequence of
processes of normal distribution sampling for yi are ap-
peared. Due to (6), the left or right zero-truncated nor-
mal-distributed sampling is used to get posterior values.
In each sampling, based upon (6) and (1) as step (b) be-

Using MCMC Probit Model to Value Coastal Beach Quality Improvement111



low, all of n original samples (yi, i = 1 to n) are revalued
for estimating the hyper-parameters.
The Gibbs sampling MCMC steps can be organized as
follows.
1) The initial value is conveniently
assigned using OLS results with



0
02
, 



 

0

1, 



X
XX
y




 
0
2

 
 


yX yX 


0
1
1,1, ,1 n



nk , as well as
and v = 200 is a fixed value for sim-
plifying calculation.
2) Given


,, ,v 


jjjjj


to sample in step
j. Referred to i, in (6) to sample z1, ,in

j
y
1
i
z
from
normal distribution for left zero-truncation if

and
right zero-truncation if .
0
i
z

3) Draw conditional on

1j


j

and

j

using

j

and (3), which means calculating the mean and
variance of depended on

1j

 
j

in last loop.
4) Draw conditional on

and

1j

 
j

1

j

us-
ing (4), which means deciding in (4) after com-
puting , randomly drawing
and using

1j

1j

 
jj



1
11 


j
yx 




2n

j

.
5) Draw conditional on and

1j


j


1

1

j

using (5), which means deciding in (5) after
computing , randomly
drawing and using .

1j


j




1v



1
11  


j
jj
yx


1j

1
2

6) Express a sampling route from step (2-5), repeat the
route 3000 times, and obtain Markov chain {s1001,
s1002, , s3000} after deleting the first 1000 set of
data.

In this process, a Bayesian regression approach is pre-
sented for the chief purpose of getting hyper parameters
β. According to the steps above, the Mean [β(1001), β(1002),
, β(3000)], a point estimator of β, can be easily achieved.
Hereto the estimated β of MCMC approach together with
β of MLE point estimator are obtained in use to value
WTP of coastal beachquality improvement below.

3. WTP Estimators
Transform Equation (1) to (12) after retaining variable
BID and calculating the remainder to get estimated con-
stant α replaced explained variables with respective
means.
ˆ
ˆ ˆ
x
y
x

  (12)
Using the symmetrical property of the PDF curve for a
standard normal distribution, we can set up F(y) = 0.5 in
(7), from which the WTP median of equation (12) can be
computed based on (13). Using Equations of (9) and (12),
WTP mean can be obtained as through Equation (14).


ˆ
ˆ
x
Median WTP

 (13)




2
ˆ12
ˆˆ
ˆˆ exp2
x
x
x
Median WTPX
x
dx x






 

 


 (14)
4. Statistical Analyses
4.1. Variables and Empirical Data
Tourism site survey was conducted from September 25
to October 10 in 2009 lasting for 15 days. Of which one
week (Oct.1 - 7) is the Chinese national holiday that is
so-called “golden week” period. The selected survey
sites included four primary tourism sites in Dalian of
northeastern China, including Tiger Beach Park, Fujiaz-
huang Bathing Beach, Xinghai Square Beach, and Xing-
hai Park. A pilot survey was conducted for pretest pur-
pose before a formal interview survey was implemented.
The survey sampled 1 276 individual tourists, of which 1
206 observations are valid responses after eliminating
those incomplete survey response questionnaire. Thus,
the effective survey response rate was 94.5%. The statis-
tical descriptive information is listed in Table 1.
Variable YAN is binary choice dependent variable
which is specified as ‘1’ given a “Yes” response, and ‘0’
for “No” response. BID is the priority variable which
represents WTP of individual interviewee and it is la-
beled as 7-levels of payment including Ұ5, Ұ10, Ұ20,
Ұ50, Ұ100, Ұ200 and Ұ500. To fulfill with DC type of
questionnaire design requirements, the number of tourists
surveyed correspondent to each level of WTP is ap-
proximately equivalent. Variable AGE is specified 1-5
categories, in which ‘1’ = below 15, ‘2’ = above 15 and
below 25, ‘3’ = above 25 and below 40, ‘4’ = above 40
and below 60, and ‘5’ = above 60. Variable EDU (Edu-
cation) is characterized 6 categories: ‘1’ = elementary
school graduate and below, ‘2’ = high or vocational
school graduate, ‘3’ = junior college graduate, ‘4’ = col-
lege or university graduate, ‘5’ = master, and ‘6’ = doctor.
Variable INC (Income) is specified as 1 to 10 categories:
(US$ 1 = RMBҰ6.83) ‘1’ = less than or equal to 500, ‘2’ =
500-999, ‘3’ = 1,000-1,999, ‘4’ = 2,000-2,999, ‘5’ =
3,000-3,999, ‘6’ = 4,000-5,999, ‘7’ = 6,000-7,999, ‘8’ =
8,000-10,000, ‘9’ = 10,000-20,000, and ‘10’ = greater
than 20,000. Variable RKM represents a respondent’s
round trip travel distance (km). Variable SW, VG, FG ,
YT, and SP are recreational activity variables which re-
spectively stands for swimming, sea-sighting and stroll-
ing, fishing, yachting, and play game on the sand. Each
of them is also characterized as ‘0’ or ‘1’ dummy vari-
able.

Using MCMC Probit Model to Value Coastal Beach Quality Improvement 112
Table 1. The variables and descriptive statistics of survey data.
Variables Mean Min. Max. Variable evaluation and number of responses
YAN 0.526 Evaluated ‘0’ = 634; Evaluated ‘1’ = 572
5 10 20 50 100 200 500
BID 129. 718 5 500
158 185 158 165 166 204 170
1 2 3 4 5
AGE 2.949 1 5
3 372 569 208 54
1 2 3 4 5 6
EDU 3.322 1 6
84 219 281 480 131 11
1 2 3 4 5 6 7 8 9 10
INC 3.667 1 10
230 69 252 284 189 106 42 22 8 4
RKM 582.570 6 4127
SW 0.256 0 1 Evaluated ‘0’ = 901; Evaluated ‘1’ = 309
VG 0.426 0 1 Evaluated ‘0’ = 692; Evaluated ‘1’ = 514
FG 0.056 0 1 Evaluated ‘0’ = 1138; Evaluated ‘1’ = 68
YT 0.049 0 1 Evaluated ‘0’ = 1147; Evaluated ‘1’ = 59
SP 0.037 0 1 Evaluated ‘0’ = 1145; Evaluated ‘1’ = 45
4.2. Results and Discussion
Based on Equations of (12), (13) and (14), the median
WTP and mean WTP can be computed through using
explanation variables show in Table 2, respectively,
where and
.
 
166.99
MLE MLE
Mean WTPMedianWTP
 
168.20
MCMC MCMC
WTPMedian WTP

Mean
In Table 2, statistical tested were conducted to evalu-
ate the regression model performance. It turns out that
there are three asymptotically equivalent statistical tests
including the likelihood ratio statistic, the Wald statistic,
and the Lagrange multiplier statistic, which can measure
goodness-of-fit and joint significance of all coefficients
except the constant, but McFadden pseudo R2 and the
likelihood ratio test are commonly used. In these two
models, the test results are almost identical with each
other. McFadden pseudo R2 and the likelihood ratio can
be used to evaluate a model’s goodness-of-fits, and they
all reach excellent level of significance in both models.
T-test indicates that all explanatory variables reach 0.10
or better statistical significance except for variables of
SW and SP. These highly consistent results suggest that
the MCMC Probit model is effective method for DC-
CVM type of analysis.
In estimating for both MLE parameters and hy-
per-parameters of MCMC, two different models were
used and both got consistent t-statistics as p-value indi-
cated, which suggest that all those main estimators are
acceptable for the WTP estimations. Thus, in case a re-
searcher is mainly interested in the study procedure to
deal with complicated problems, a non-parameter esti-
mation program should be recommended.
Connotation reflected through coefficients of explana-
tory variables transmits the information that BID, AGE,
and activities variables are negatively correlated with
latent utility difference. The negative signs of coeffi-
cients have different meaning for WTP measurement
because BID’s is a denominator and the other explana-
tory variables are embedded in the numerator of WTP
calculation. Coefficient modulus of BID expresses an
inverse ratio relationship with WTP, while the other ex-
planatory variables are truly negative correlations with
WTP.
5. Conclusions
In this paper, a MCMC Gibbs sampling Probit model is
used to evaluate the coastal beach quality improvement.
From an empirical study perspective, the procedure can
be used to estimate economic value for multiple study
fields including but not limited to healthy, risk, transpor-
tation, resources and environment and ecology compen-
sation, etc. In comparison with traditional MLE Probit
model, MCMC Probit model achieves very consistent
results, which suggest that the WTP estimation using
both methods is more robust.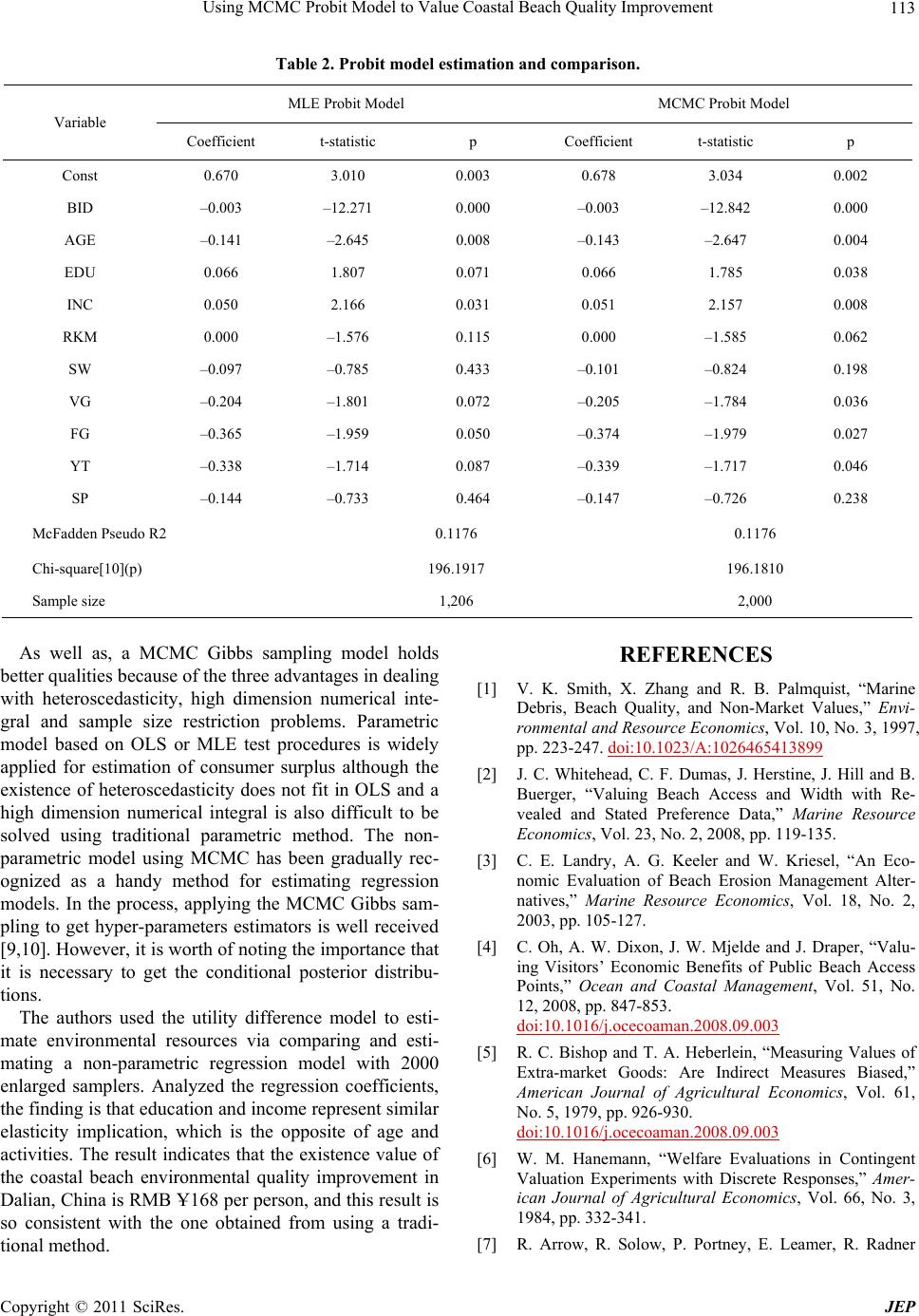

Using MCMC Probit Model to Value Coastal Beach Quality Improvement113
Table 2. Probit model estimation and comparison.
MLE Probit Model MCMC Probit Model
Variable
Coefficient t-statistic p Coefficient t-statistic p
Const 0.670 3.010 0.003 0.678 3.034 0.002
BID –0.003 –12.271 0.000 –0.003 –12.842 0.000
AGE –0.141 –2.645 0.008 –0.143 –2.647 0.004
EDU 0.066 1.807 0.071 0.066 1.785 0.038
INC 0.050 2.166 0.031 0.051 2.157 0.008
RKM 0.000 –1.576 0.115 0.000 –1.585 0.062
SW –0.097 –0.785 0.433 –0.101 –0.824 0.198
VG –0.204 –1.801 0.072 –0.205 –1.784 0.036
FG –0.365 –1.959 0.050 –0.374 –1.979 0.027
YT –0.338 –1.714 0.087 –0.339 –1.717 0.046
SP –0.144 –0.733 0.464 –0.147 –0.726 0.238
McFadden Pseudo R2 0.1176 0.1176
Chi-square[10](p) 196.1917 196.1810
Sample size 1,206 2,000
As well as, a MCMC Gibbs sampling model holds
better qualities because of the three advantages in dealing
with heteroscedasticity, high dimension numerical inte-
gral and sample size restriction problems. Parametric
model based on OLS or MLE test procedures is widely
applied for estimation of consumer surplus although the
existence of heteroscedasticity does not fit in OLS and a
high dimension numerical integral is also difficult to be
solved using traditional parametric method. The non-
parametric model using MCMC has been gradually rec-
ognized as a handy method for estimating regression
models. In the process, applying the MCMC Gibbs sam-
pling to get hyper-parameters estimators is well received
[9,10]. However, it is worth of noting the importance that
it is necessary to get the conditional posterior distribu-
tions.
The authors used the utility difference model to esti-
mate environmental resources via comparing and esti-
mating a non-parametric regression model with 2000
enlarged samplers. Analyzed the regression coefficients,
the finding is that education and income represent similar
elasticity implication, which is the opposite of age and
activities. The result indicates that the existence value of
the coastal beach environmental quality improvement in
Dalian, China is RMB Ұ168 per person, and this result is
so consistent with the one obtained from using a tradi-
tional method.
REFERENCES
[1] V. K. Smith, X. Zhang and R. B. Palmquist, “Marine
Debris, Beach Quality, and Non-Market Values,” Envi-
ronmental and Resource Economics, Vol. 10, No. 3, 1997,
pp. 223-247. doi:10.1023/A:1026465413899
[2] J. C. Whitehead, C. F. Dumas, J. Herstine, J. Hill and B.
Buerger, “Valuing Beach Access and Width with Re-
vealed and Stated Preference Data,” Marine Resource
Economics, Vol. 23, No. 2, 2008, pp. 119-135.
[3] C. E. Landry, A. G. Keeler and W. Kriesel, “An Eco-
nomic Evaluation of Beach Erosion Management Alter-
natives,” Marine Resource Economics, Vol. 18, No. 2,
2003, pp. 105-127.
[4] C. Oh, A. W. Dixon, J. W. Mjelde and J. Draper, “Valu-
ing Visitors’ Economic Benefits of Public Beach Access
Points,” Ocean and Coastal Management, Vol. 51, No.
12, 2008, pp. 847-853.
doi:10.1016/j.ocecoaman.2008.09.003
[5] R. C. Bishop and T. A. Heberlein, “Measuring Values of
Extra-market Goods: Are Indirect Measures Biased,”
American Journal of Agricultural Economics, Vol. 61,
No. 5, 1979, pp. 926-930.
doi:10.1016/j.ocecoaman.2008.09.003
[6] W. M. Hanemann, “Welfare Evaluations in Contingent
Valuation Experiments with Discrete Responses,” Amer-
ican Journal of Agricultural Economics, Vol. 66, No. 3,
1984, pp. 332-341.
[7] R. Arrow, R. Solow, P. Portney, E. Leamer, R. Radner

Using MCMC Probit Model to Value Coastal Beach Quality Improvement 114
and H. Schuman, “Report of the NOAA Panel on Con-
tingent Valuation,” 1993.
http://www.darrp.noaa.gov/library/pdf/cvblue.pdf
[8] J. Geweke, “Bayesian Treatment of the Independent Stu-
dent t Linear Model,” Journal of Applied Econometrics,
Vol. 8, No. 1, 1993, pp.19-40.
doi:10.1002/jae.3950080504
[9] S. Chib and E. Greenberg, “Markov Chain Monte Carlo
Simulation Methods in Econometrics,” Econometric
Theory, Vol. 12, No. 3, 1996, pp. 409-431.
doi:10.1017/S0266466600006794
[10] R. E. Kass, B. P. Carlin, A. Gelman, and R. M. Neal,
“Markov Chain Monte Carlo in Practice: A Roundtable
Discussion,” The American Statistician, Vol. 52, No. 2,
1998, pp. 93-100. doi:10.2307/2685466