Journal of Computer and Communications, 2014, 2, 42-47
Published Online January 2014 (http://www.scirp.org/journal/jcc)
http://dx.doi.org/10.4236/jcc.2014.22008
OPEN ACCESS JCC
Image Enhancement in Coherent Optical Amplification by
Photorefractive Crystals
Danyu Chen, Fengchun Tian, Ying Liu, Youwen Hu, Liang Han
College of Communication Engineering, Chongqing University, Chongqing, China.
Received November 2013
ABSTRACT
In this paper, a model of two-wave mixing in the photorefractive crystal, which takes account of the difference in
spatial frequency in a beam, has been built to study the image enhancement effect in coherent optical amplifica-
tion. Based on the theoretical analysis of the model, the gain distribution for each pixel in the signal beam has
been obtained. It shows that the unevenness of the gain is induced by the difference in spatial frequency in the
beam. The factors that impact on the uniformity of image enhancement have been analyzed. As an example, the
effects of these factors in a given photorefractive crystal have been studied through simulation.
KEYWORDS
Coherent Optical Amplification; Photorefractive Effect; Image Enhancement; Unevenness of Gain
1. Introduction
Coherent optical amplification, as an interesting pheno-
menon of great research and application value in nonli-
near optics, has received growing interest in the past four
decades. In a photorefractive crystal, two-wave mixing
can be explained as the nonlinear interaction of intensity
and phase between two incident beams through the pho-
torefractive effect [1-3]. Plenty of effective applications
of two-wave mixing have been applied to different fields,
such as real-time holography, self-pumped phase conju-
gation, coherent image amplification, optical storage, etc.
[4,5].
As for two-dimensional image enhancement, it is a
practical way to make use of photorefractive crystals in
two-wave mixing arrangements because of the relative
convenient operation and the potential for high gain [6,7].
The gain non-uniformity will introduce serious wave-
front distortion and apparent polarization state degrada-
tion to the output beam. Especially the induced perturba-
tion between the spatial intensity and phase of the beam
will cause small-scale self-focusing in the beam and even
devastating damage to the elements in the light path.
However, most research on coherent image amplification
by two-wave mixing in previous literature only empha-
sized on the condition of a single spatial frequency
[1,8,9].
In this paper, the unevenness of image enhancement in
coherent optical amplification by photorefractive crystals,
which takes the difference in spatial frequency in a beam
into account, has been studied in detail.
2. Theoretical Analysis
The model of two-wave mixing in previous literatures,
which are concentrated on the situation for a single spa-
tial frequency, has been presented in Figure 1.
As seen in Figure 1, the two beams
1
I
and
2
I
enter
into a photorefractive crystal symmetrically. The interfe-
rence intensity
()Ix
and refractive index n(x) distribut-
ing Equations [6] can be expressed as
0
( )(1cos)I xImkx= +
, (1)
0
( )+cos()
s
n xnmnkx ψ =∆+
, (2)
where
12
12
2II
mII =+
is the intensity modulation depth;
s
n∆
is the saturation value of photo induced refractive
index change; k is the value of index gratings wave vec-
tor;
ψ
is the phase offset between the interference in-
tensity pattern and refractive index gratings.
In order to study the unevenness of gain in coherent
optical amplification by photorefractive crystals, a model
that takes account of the difference in spatial frequency
in a beam has been built. And the geometrical configura-
tion has been presented in Figure 2.

Image Enhancement in Coherent Optical Amplification by Photorefractive Crystals
OPEN ACCESS JCC
43
Figure 1. Previous model of two-wave mixing. This is a
geometrical configuration with regard to a single spatial
frequency.
Figure 2. New model of two-wave mixing. This is a geome-
trical configuration in view of the different spatial frequen-
cies in a beam.
As seen in Figure 2, C is the optical axis of the crystal,
which is parallel to x-axis. Assuming the pump and sig-
nal beam enter into the medium symmetrically with re-
spect to the normal (z-axis) from the left side (z = 0). The
two beams couple with each other in the crystal, which
leads to the enhancement of the signal beam at the ex-
pense of the pump beam intensity decrease. For both the
pump and signal beam, which are superposition of cracks
of light, the optical field analytical expression on each pixel
can be represented by ( , )exp[i(( , ))]pqt pq
ω
−⋅A ar
and
(, )exp[i((, ))]
mnt mn
ω
−⋅B br
separately, where
(,)pq
indicates the spatial locations of light on individual pixel
in the pump beam, and
(,)mn
similarly in the signal
beam; p = 1, 2, …, P; q = 1, 2, …, Q; m = 1, 2, …, M; n
= 1, 2, …, N;
(,)pqa
and
(,)mnb
are separately the
wave vectors on each pixel in the pump and signal beam,
which can be expressed with the coordinate system in
Figure 2.
As a small divergence angle will be induced with the
spatial propagation in Gaussian beam shot from a laser
[10], the pump and signal waves span a rather small an-
gular range, which results in different spatial frequencies
in a beam. The offsets of the propagation direction on
each pixel to the average propagation direction are
represented by
(,)
ppq
δ
and
(,)
smn
δ
separately for the
pump and signal waves. Therefore, when entering into
the crystal, the incident angle on each pixel in the pump
and signal beam can be represented separately by
(,)= (,)
pp
pq pq α θδ +
and
(,)= (,)
ss
mn mn β θδ +
,
where
p
θ
and
s
θ
indicate the average incident angle
of the pump and signal beam, respectively. Ordinarily,
==
sp
θθθ
is assumed.
As is known, the far-field small divergence angle
δ
of laser beams can be figured out by the formula [11]
0
0
2
2= =2
L λλ
δω
πω π
,
, (3)
where L is the resonant cavity length of the laser,
λ
is
the wavelength of the beams. Consequently, for the pump
and signal waves,
(,)
p
pq δ
and
(,)
smn
δ
vary over a
range of
δ ±
separately, i.e. , the incident angle on each
pixel in the signal beam
(,)mn β
range from
θδ −
to
θδ +
.
The interference intensity of the pump and signal
waves in the crystal, which has been deduced from Equa-
tion (1), can be expressed as
( )()()
( )
( )
*
011 11
*
11 11
*
1 11
1,,exp i(,)(,)
2
1(,)(, )expi(,)(, )
4
1( ,)(,)expi( ,)(,)
4
Q P MN
pq mn
QQ PP
pq xy
p xq y
N MN
n jk
nk
IIA pqBmnpqmn
ApqAxypqxy
BmnBjkmnjk
= == =
= == =
≠≠
== =
≠

=+ −⋅



+ −⋅


+ −⋅


∑∑ ∑∑
∑∑ ∑∑
∑∑
abr
aar
b br
1
c.c.
M
m
mj
=
≠

+



∑∑
(4)
where
011 11
=( , ;0)(, ;0)
Q
P MN
ps
pq mn
IIpqI mn
= == =
+
∑∑ ∑∑
is the total in-
tensity of the incident pump and signal beam; c.c. indi-
cates the complex conjugate of the previous term.
Based on Equation (2), the refractive index distribu-
tion can then be approximated as
( )
* 1
011 11
0
i(,)(,)expi (,)(,)
2
c.c.
Q P MN
pq mn
n
nnApqB mnpqmn
I
= == =
=+ −⋅ 

+
∑∑∑∑
abr
(5)
where
0
n
is the refractive index of the crystal when no
light is present;
1
n
is the modulation factor of refractive
index, which depends on the spacing and direction of the
grating, as well as on the material properties of the crys-
tal, e.g., the electro-optic coefficient. Equ ation (5) is
solved for the steady state so that the amplitudes
(,)Apq
and
(,)
Bmn are taken to be time independent.
With this and the slowly varying amplitude approxi-
mation [12], Maxwell’s scalar equations yield the fol-
lowing coupled amplitude equations
2
11
0
1
(,)
d(,;) 1
( ,;)(,;)(,;)
d2
π
1, 2,,;1, 2,,;(,)=cos(, )
MN
p
mn
p
pq
Apqr BmnrApqrApqr
rI
n
pP qQpqpq
γσ
γλα
= =
=−−
=…=…
∑∑
(6)

Image Enhancement in Coherent Optical Amplification by Photorefractive Crystals
OPEN ACCESS JCC
44
2
11
0
1
s
(,) d( ,;)1
(,;)(,;)( ,;)
d2
π
1, 2,,;1, 2,,;(,)=cos(, )
Q
P
s
pq
mn
Bmnr Apqr BmnrBmnr
rI
n
mM nNmnmn
γσ
γλβ
= =
= −
=…=…
∑∑
(7)
where
σ
is the absorption coefficient of the crystal,
which is regulated by the wavelength of the incident
beam.
Since the relation between the intensities and ampli-
tudes of the incident beams are
2
(,;) (,;)
p
I pqrApqr=
and
2
( ,;)( ,;)
s
I mnrBmnr=
, the coupled intensity equ-
ations are given by
11
0
d (,;)(,)
=( ,;)(,;)(,;)
d
1, 2,,;1, 2,,;(,)=2(,)
MN
pp
sp p
mn
pp
I pqrpqImnrI pqrI pqr
rI
pP qQpqpq
σ
γ
= =
Γ
−−
=…=…Γ
∑∑
(8)
11
0
s
d(,;) (,)
=(,;)( ,;)(,;)
d
1, 2,,;1, 2,,;(,)=2(,)
Q
P
ss ps s
pq
s
I mnrmnIpqrI mnrI mnr
rI
mM nNmnmn
σ
γ
= =
Γ−
=… =…Γ
∑∑
(9)
In the assumed diffusion driven scenario, the phases of
the beams are decoupled so that the intensity Equations
(8) and (9) describe the two-wave mixing process com-
pletely.
With Equation (8) and Equation (9), one can integrate
to yield the intensity versus effectively acting distance r
on each pixel in the signal beam, which can be norma-
lized by the initial intensity as
11
( ,)
11
(, ;0)
( ,;)1
==
(, ;0)1(, ;0)
s
Q
P
p
pq
r
smnrM N
s
s
mn
I pq
I mnrheh
I mnhe I mn
σ
= =
−
−Γ
= =
+
+
∑∑
∑∑
,
. (10)
Therefore, the gain, which is defined as the intensity
ratio of the output signal wave in the presence of a pump
beam to that in the absence of a pump beam, can be giv-
en by
( ,)
(, ;)1
(,)=
(, ;0)1
=cos(, )
s
l
smnl
s
i
I mnlh
Gmn e
I mnhe
d
lmn
σ
β
−
−Γ
+
=+,
, (11)
where d is the thickness of the crystal,
(,)
i
mn β
is the
angle between the propagation direction and the normal
(z-axis) on each pixel in the signal beam inside the crys-
tal, and l is the effective interaction length on individual
pixel in the signal beam.
To perform calculation of the gain, the expression of
intensity coupling coefficient
(,)
s
mnΓ
[13], presented
below, can be insert into Equation (11).
22
cos2(, )
sin(, )
(,).
cos(,)
1sin(, )
i
si
mn
A mn
mn mn
B mn
β
β
β
β
−
Γ=
+
. (12)
In Equ ation (12), the related parameters are included
in coefficient A and B, which can be given by
23
2
8
= ()
B
eff
nkT
AK
e
π
γξ λ
, (13)
1/2
0
=() .4
eff
B
Ne
BkT
λ
εε π
, (14)
where eff
γ
is the effective electric-optic coefficient; n is
the refractive index;
()K ξ
is the recombination con-
stant, which is fixed when the value of
2/k πλ =
is set;
eff
N
is the effective charge density, which is regulated
by the wavelength of the incident beams;
B
k
is the
Boltzmann constant; T is the absolute temperature; e is
the charge on the electron;
λ
is the wavelength of the
incident beams.
According to the analysis above, the gain non- unifor-
mity in the signal beam, which indicates the unevenness
for image enhancement, is induced by the difference in
spatial frequency in the beam. As seen in Equations
( 11-14), the factors, which impact on the unevenness of
gain in the signal beam, are the crystal thickness d, the
incident angle
(,)mn
β
, and the wavelength
λ
.
3. Simulation and Discussion
The non-uniformity of gain can be measured with the
relative standard deviation
γ
= SD/AVG. Here, AVG
and SD are the mean value and standard deviation of the
gain in the signal image beam, respectively. The gain
non-uniformity is negligible compared with the value of
gain when
γ
reaches a low enough value. The usual
requirement is
γ
= 1%.
In this paper, the numerical simulation for two-wave
mixing is based on the model analyzed above. Assuming
the signal beam and the pump beam are split from a laser
beam at a ratio of 1:1120. Then the two of them recom-
bines at a photorefractive
() ()
3
Fe 0.04wt%:Ce 0.1wt%:LiNbO
crystal from the
same side with the average incident angle
==
sp
θθθ
.
Three scenarios with different wavelengths have been
analyzed to obtain the gain distribution in the signal im-
age beam.
3.1. Argon Laser at λ = 488 nm
In the first scenario, the light source is an argon laser
with a cavity length of L = 150 cm operating at wave-
length 488 nm, in which case the crystal has the parame-
ters of 1 =21.2cm σ
− and
15 3
2.9 10 cm
eff
N
−
= ×
ac-
cording to [14]. Substituting
λ
and L into Equation (3)
yields the far-field small divergence angle of the laser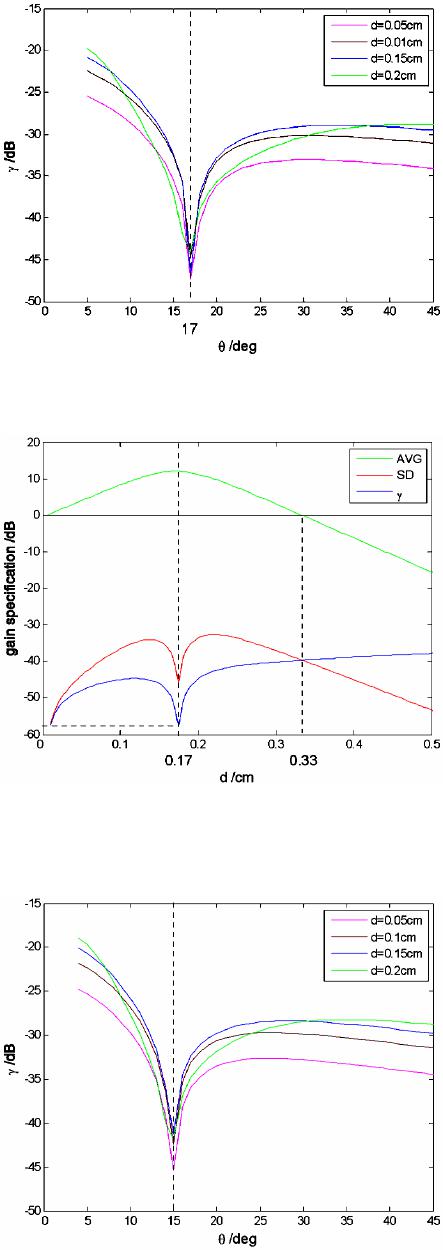

Image Enhancement in Coherent Optical Amplification by Photorefractive Crystals
OPEN ACCESS JCC
45
beam:
=0.026075 δ

.
Computer-generated plots of the non-uniformity of
gain versus the average incident angle
θ
for different
values of d have been presented in Figure 3. The effects
of angle
θ
on
γ
are similar for different values of d.
γ
decreases with the increasing
θ
, reaches a minimum,
then increases and afterwards decreases again. For each
value of d,
γ
reaches its minimum with a same value of
θ
, i.e.,
17

.
The values of AVG, SD and
γ
versus d for the op-
timal average incident angle
=17
opt
θ

are presented in
Figure 4. Within the 0 - 0.33 cm range of d,
γ
increas-
es with the increasing d, then decreases to a minimum
and afterwards increases again. Particularly, the optimal
thickness of the crystal
opt
d
, in which case
γ
reaches
its minimum 0.00016%, is turned out to be 0.17 cm.
3.2. Argon Laser at λ = 514.5 nm
The second scenario is that, the operating wavelength of
the argon laser used in the first scenario is changed to
514.5 nm, in case the crystal has the parameters of
1
=16.2cm σ
− and
15 3
1.9 10 cm
eff
N
−
= ×
according to
[14]. What’s more, the far-field small divergence angle
of the laser beam is turned into
=0.026774 δ

.
The values of
γ
versus angle
θ
for different values
of d have been presented in Figure 5. The optimal aver-
age incident angle
opt
θ
, which will guarantee the mini-
mum value of
γ
regardless of the value of d, is ap-
peared to be
15

.
Simulation results of AVG, SD and
γ
versus d for
opt
θ are presented in Figure 6. Within the 0-0.43cm
range of d,
γ
increases with the increasing d, then bas-
ically remain unchanged.
3.3. He-Ne Laser at λ = 632.8 nm
The last scenario is that, the argon laser used in the first
scenario is changed for a He-Ne laser with a cavity
length of L = 30 cm at wavelength 632.8 nm, in which
case the crystal has the parameters of
1
=0.7cm σ
−
and
15 3
0.1 10cm
eff
N
−
= ×
. Besides, the far-field small di-
vergence angle of the laser beam is turned out to be
=0.066395 δ

.
The results of
γ
with varying angle
θ
for different
values of d are presented in Figure 7. Note that the fluc-
tuation amplitude of
γ
is larger than that in the pre-
vious two scenarios. The optimal average incident angle
opt
θ
is
4

.
The values of AVG, SD and
γ
versus d for opt
θ
have been presented in Figure 8.
γ
increases with the
increasing d, then decreases to a minimum and after-
wards increases again. The minimum value of
γ
(0.000184%) can be reached with
opt
d
= 0.54 cm.
Figure 3. Values of γ versus average incident angle θ for
several values of crystal thickness d with λ = 488 nm.
Figure 4. Values of AVG, SD and γ versus crystal thickness
d for optimal average incident angle
o
= 17
opt
θ
with λ =
488 nm.
Figure 5. Values of γ versus average incident angle θ for
several values of crystal thickness d with λ = 514.5 nm.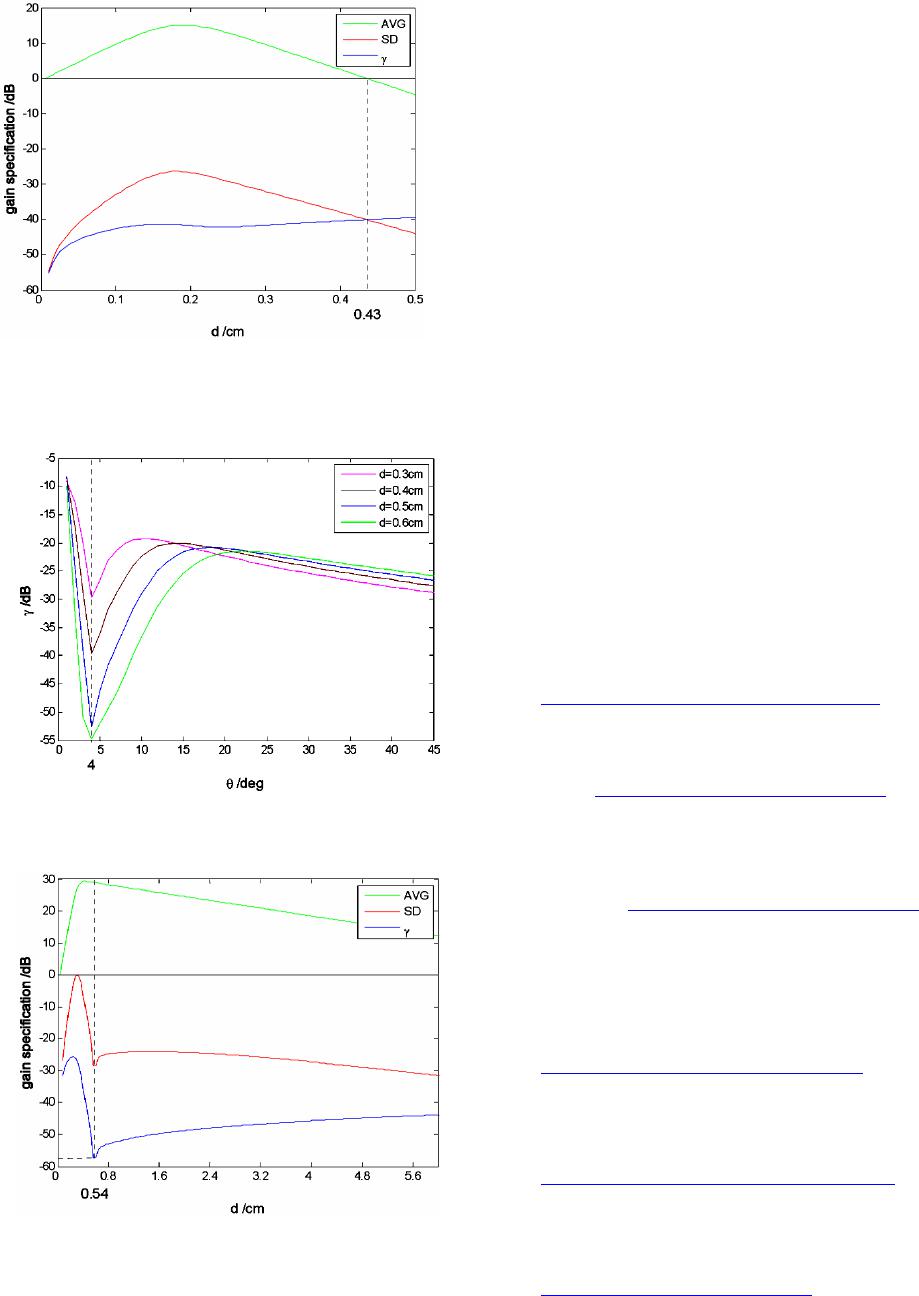

Image Enhancement in Coherent Optical Amplification by Photorefractive Crystals
OPEN ACCESS JCC
46
Figure 6. Values of AVG, SD and γ versus crystal thickness
d for optimal average incident angle
o
= 15
opt
θ
with λ =
514.5 nm.
Figure 7. Values of γ versus average incident angle θ for
several values of crystal thickness d with λ = 632.8 nm.
Figure 8. Values of AVG, SD and γ versus crystal thickness
d for optimal average incident angle
o
=4
opt
θ
with λ =
632.8 nm.
4. Conclusion
In short, to explore the unevenness of image enhance-
ment in coherent optical amplification by photorefractive
crystals, a model in view of different spatial frequency in
a beam has been built. It has been proved that the factors
which impact on the unevenness of image enhancement
are: the thickness of photorefractive crystal, the incident
angle on each pixel in signal image beam, and the wave-
length of incident beams. As an example, the effects of
these factors in photorefractive
() ()
3
Fe 0.04wt%:Ce 0.1wt%:LiNbO
crystal have been
re- searched through simulation. It turns out that a consi-
derable non-uniformity of
γ
= 0.00016% can be rea-
ched when the wavelength of the incident beam is 488
nm (at
=17 θ

, d = 0.17 cm).
Acknowledgements
The authors thank the National Natural Science Founda-
tion of China (No. 61071190, No. 61171158) and the
Fundamental Research Funds for the Central Universities
of China (No. CDJZR12160010) for support.
REFERENCES
[1] N. V. Kukhrarev, V. B. Markov, S. G. Odulov, M. S.
Soskin and V. L. Vinetskii, “Holographic Storage in
Electro-Optic Crystals. I. Steady State”, Ferroelectrics,
Vol. 22, No. 1, 1978, pp. 949-953.
http://dx.doi.org/10.1080/00150197908239450
[2] M. C. Søren, B. Jensen, J. P. Huignard and P. M. Petersen,
“Two-Wave Mixing in a Broad-Area Semiconductor Am-
plifier,” Optics Express, Vol. 14, No. 25, 2006, pp. 12373-
12379. http://dx.doi.org/10.1364/OE.14.012373
[3] M. C. Søren, B. Jensen, J. P. Huignard and P. M. Petersen,
“Nonlinear Gain Amplification Due to Two-Wave Mix-
ing in a Broad-Area Semiconductor Amplifier with Mov-
ing Gratings,” Optics Express, Vol. 16, No. 8, 2008, pp.
5565-5571. http://dx.doi.org/10.1364/OE.16.005565
[4] P. Günter and J. P. Huignard, “Photorefractive Materials
and Their Applications II,” Springer-Verlag, Berlin, 1989.
[5] N. Katyal, Natasha, A. Roy and A. Kapoor, “The Influ-
ence of Pump Beam Polarization on the Signal Beam, in
TWM in Photorefractive Crystals: Transmission Geome-
try,” Optik, Vol. 122, No. 3, 2011, pp. 207-210.
http://dx.doi.org/10.1016/j.ijleo.2009.11.028
[6] J. P. Huignard and A. Marrakchi, “Coherent Signal Beam
Amplification in Two-Wave Mixing Experiments with
Photorefractive Bi12SiO20 Crysta ls,” Optics Communica-
tions, Vol. 38, No. 4, 1981, pp. 249-254.
http://dx.doi.org/10.1016/0030-4018(81)90392-8
[7] Y. Fainman, E. Klancnik and S. H. Lee, “Optimal Cohe-
rent Image Amplification by Two-Wave Coupling in
Photorefractive BaTiO3,” Optical Engineering, Vol. 25,
No. 2, 1986, pp. 228-234.
http://dx.doi.org/10.1117/12.7973810

Image Enhancement in Coherent Optical Amplification by Photorefractive Crystals
OPEN ACCESS JCC
47
[8] P. Tayebati and D. Mahgerefteh, “Theory of the photore-
fractive effect for Bi12SiO20 and BaTiO3 with shallow
traps,” Journal of the Optical Society of America B, Vol.
8, No. 5, 1991, pp. 1053-1064.
http://dx.doi.org/10.1364/JOSAB.8.001053
[9] B. G. Peng, F. Chen, Y. Tan and D. Kip, “T wo-Wave
Mixing of Ion-Implanted Photorefractive Waveguides in
Near-Stoichiometric Fe:LiNbO3 Crystals,” Optics Mate-
rials, Vol. 33, No. 6, 2011, pp. 773-776.
http://dx.doi.org/10.1016/j.optmat.2010.12.016
[10] Jiabi Chen, “Principle and Application of Laser,” Tongp-
ing Han, Beijing, 2004.
[11] D. Z. Anderson and R. Saxena, “Theory of Multimode
Operation of a Unidirectional Ring Oscillator Having
Photorefractive Gain: Weak Field Limit,” Journal of the
Optical Society of America B, Vol. 4, No. 2, 1987, pp.
164-176. http://dx.doi.org/10.1364/JOSAB.4.000164
[12] Z. Y. Li, B. Y. Gu and G. Z. Yang, “Slowly Varying
Amplitude Approximation Appraised by Transfer-Matrix
Approach,” Physical Review B, Vol. 60, No. 15, 1999, pp.
10644-10647.
http://dx.doi.org/10.1103/PhysRevB.60.10644
[13] C. H. Ya ng and L. Sun, “Photorefractive Nonliear Optical
Materials: LiNbO3 Crystals,” Jiafu Yang, Beijing, 2009.
[14] T. K. Yadav, M. K. Maurya and R. A. Yadav, “Effect of
Photoconductivity and Oscillation Frequency Shift on the
Signal Beam Intensity in Two Beam Coupling in Photo-
refractive Materials,” Optik, Vol. 122, No. 18, 2011, pp.
1607-1614. http://dx.doi.org/10.1016/j.ijleo.2010.10.011