An Improved EZW Hyperspectral Image Compression
OPEN ACCESS JCC
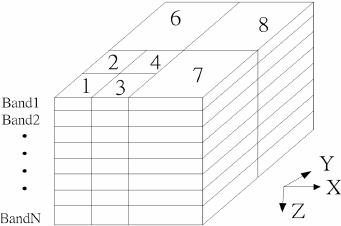
Figure 4. 2-D wavelet transform coefficients are stored in a
data cube.
level decomposition on each band.
The DWT has two important properties which are
critical for image compression:
1) Energy packing: When an image is wavelet trans-
formed, the transformed image has energy compaction in
spectral dimensions, that is, the wavelet coefficients in
the higher level subbands will, on average, be larger than
those in the lower level subbands.
2) Self-similarity: A wavelet coefficient at a higher
level subband and all wavelet coefficients of the same
spatial orientation at lower level subbands have certain
predictable relationships.
4. Shapiro’s EZW Algorithm
Shapiro invented his Embedded Zerostree Wavelet
(EZW) algorithm taking advantage of the wavelet trans-
form [2]. The EZW algorithm implements a progressive,
embedded image coding method based on the zerotrees
of data structure. All currently significant bits at the same
bitplane together and recursively encodes other pixels for
the next significant bitplane until reaching the least sig-
nificant bitplane. As a result, the lower significant bits
are embedded behind the higher significant bits, so that a
decoder quickly displays a low quality image and better
quality as more bits are received.
We notethree crucial components that make Shapiro’s
EZW algorithm effectivein image compression. First,
due to energy packing, these wavelet coefficients in
higher level subbands could be scanned earlier than oth-
ers in low level subbands. In other words, larger coeffi-
cients will be encoded first. In addition, both receiver and
transmitter know what scanning order is selected such
that it does not include the scanning order in the over-
head. Scanning order used in this paper is Morton scan.
Second, the quad-tree is the fundamental idea of the
EZW algorithm to interpolate the relations among wave-
let coefficients in different subbands; therefore, it is set
up based on the self-similarity. The definition of the
quad-tree was introduced in [2].
There are two steps to complete EZW algorithm: the-
dominant pass and the subordinate pass. The dominant
pass keeps track of the search for significant coefficients
by labeling each pixel among these four labels: signific-
ance positive symbol (POS), significant negative symbol
(NEG), zerotree root (ZTR) and isolated zeros (IZ) in
Figures 5(a)-(c). The subordinate pass quantizes each
significant coefficient that has been found in the domi-
nant pass.
The definitions of four symbols are described below. If
a root coefficient, in absolute value, is larger than a thre-
shold, it is labeled as significant positive (POS) or sig-
nificant negative (NEG) in Figure 5(b). It implies that
some of the coefficients’ descendants are significant. An
isolated zero (IZ) is a root coefficient that is insignificant
but has some significant descendants in Figure 5(c). If
the coefficient is zerotree root (ZTR), it means the root
coefficient itself and its descendants are all insignificant
such that these descendants don’t have to be encoded in
the current iteration in Figure 5(a) .
5. Modified EZW Algorithm
We propose some modifications to simplify the conven-
tion EZW algorithm and improved the compression re-
sults. [10-13] have studied the asymmetrical 3D-DWT
decomposition that causes the asymmetrical statistics of
the transformed hyperspectral image; thus the asymme-
trical tree structure is more suitable for describing the
transformed hyperspectral image. In this paper, the 3D
asymmetric tree structure was designed according to the
properties of hybrid transforms. In Figure 4, a wavelet
coefficient at a higher subband is not only relative to all
wavelet coefficients of the same spatial orientation at
lower subbands at the same band but also in the neighbor
band. Therefore, if the approximation subband is
-by-
with -level decomposition at the
first band, while the spatial dimensions of the image are
m-by-n. Any root
in the approximation has
four immediate children at
,
(,/2 ,0),(/2 ,/2,0)
l ll
xymxmym+ ++
and
In addition, except ones in the approximation, any root (x,
y, 0) at the first band has four children located at the
same spatial orientations (2x, 2y, 0), (2x + 1, 2y, 0), (2x,
2y + 1, 0), and (2x + 1, 2y + 1, 0) on the first band and
one more child (x, y, 1) below it. Note that any pixel not
in the first band has only one child below it. The new tree
structure will continue to branch until no offspring can be
found. The new and simple definition of tree structure is
demonstrated in Figure 6. Each pixel in the low-pass
(approximation) section of band 1 is a tree root.
In addition to the four labels defined in Shapiro’s
EZW algorithm, in this study, we define two more labels,
called positive and negative ZTR (PZT and NZT) in
Figure 5(d). According to [14], they are degree-1 zero-
trees since every coefficient except the root coefficient is
all zeros. Roots of PZT and NZT are positive and nega-