Journal of Computer and Communications, 2014, 2, 20-24
Published Online January 2014 (http://www.scirp.org/journal/jcc)
http://dx.doi.org/10.4236/jcc.2014.22004
OPEN ACCESS JCC
Characteristic Analysis of White Gaussian Noise in
S-Transformation Domain
Xinliang Zhang1, Yue Qi1, Mingzhe Zhu1,2
1Department of Electronic Engineering, Xidian University, Xi’an, China; 2The Ministry Key Laboratory of Electronic Information
Countermeasure and Simulation, Xidian University, Xi’an, China.
Received October 2013
ABSTRACT
The characteristic property of white Gaussian noise (WGN) is derived in S-transformation domain. The results
show that the distribution of normalized S-spectrum of WGN follows
2
χ
distribution with two degrees of free-
dom. The conclusion has been confirmed through both theoretical derivations and numerical simulations. Com-
bined with different criteria, an effective signal detection in S-transformation can be realized.
KEYWORDS
Signal Detection; S-Transform; White Gaussian Noise;
2
χ
Distribution
1. Introduction
THE S-transform(ST) has been well studied since it was
proposed by R. G. Stockwell in 1996 [1] and has already
found applications in many fields such as geophysics [2],
mechanical systems [3] and medical signal analyses [4].
The signal processing framework in S-transformation
domain is under building and more and more ST based
methods are proposed. The most contributive works
among them were conducted by C. R. Pinnegar who ex-
tended the original ST to generalized ST [2] and pre-
sented several kinds of useful STs for specific conditions,
such as the asymmetric ST [2], the bi-Gaussian ST [5]
and the complex ST [6]. Other outstanding works were
concentrated on ST based time-frequency filtering [7],
the side effects of inverse ST [8], ST based instantaneous
frequency estimation [9] and ST based pattern recog-
nition [10,11]. However, the noise analysis in S-trans -
formation domain, which is the essential problem for
signal detection, has not been well studied yet. [11] pre-
sented an illuminating idea for noise distribution in a
specific generalized ST domain but didn’t prove it theo-
retically. In this paper, the characteristic property of
WGN in original ST domain is derived theoretically and
the conclusion is further verified by Monte Carlo method.
Its application in nonstationary signal detection is also
illustrated.
The rest of this paper is organized into as follows: In
Section 2, the proposition of WGN distribution followed
by its theoretical derivation is given. Section 3 verifies
the proposition by Monte Carlo method. In Section 4, the
performance of signal detection is illustrated by detecting
transient sinusoid signals under the constant-false-alarm-
rate (CFAR) criterion. Finally, conclusions are drawn in
Section 5.
2. Characteristic Property of WGN in ST
Domain
2.1. Proposition
The S-transform of a signal
()xt
is defined by [1]
1
(, )()exp(2)(, )
2
x
St fxjfwtfd τπττ τ
π
∞
−∞
= −−
∫
(1)
where the window function is
22
(,)exp(/ 2)wf ff ττ = −
(2 )
And the characteristic and the advantage of ST has
been sufficiently described by previous literature [2-6].
Let
2
(, )
x
S tf
be the S-spectrum of
()xt
and white
Gaussian noise
2
( )(0,)ntN σ 
; then the normalized
S-spectrum of
()nt
,
22
2(, ) /(, )
nn
S tfE S tf


(de-
noted as
2
(, )
n
NSt f
), follows
2
χ
distribution with
two degree of freedom.

Characteristic Analysis of White Gaussian Noise in S-Transformation Domain
OPEN ACCESS JCC
21
2.2. Proof
Step.1: Derive the distribution of
Re[( ,)]
n
Stf
and
Im[( ,)]
n
S tf and prove that they follow the identical
Gaussian distribution.
By definition, the S-spectrum of
()nt
can be expressed as
( )
222
,Re[( ,)]Im[(,)]
n nn
StfS tfS tf= +
(3)
Before further proceeding, let us analyze the distri-
bution of Re[( ,)]
n
S tf and Im[( ,)]
n
S tf, respectively.
The real part of
(, )
n
Stf
is given by
22
()
Re[(,)]()exp()cos(2)
2
2
n
ftf
S tfnfd
τ
τπτ τ
π
∞
−∞
−−
=
∫
(4)
Re[( ,)]
n
Stf
is the integral of
()nt
multiplied by
deterministic signals, thus the distribution of
Re[( ,)]
n
S tf is the same as
()nt
with zero mean and
its variance 2
()
Rt
σ expressed as
22
21
1 11
22
2
2 22
222
1
12
22
212 12
2
()
( )()exp()cos(2)
2
2
()
( )exp()cos(2)
2
2
()
( )()exp()
2
2
()
exp() cos(2) cos(2)
2
2
R
ftf
tEnfd
ftf
n fd
ftf
En n
tf ff dd
f
τ
στπτ τ
π
τ
τπτ τ
π
τ
ττ
π
τπτπτ ττ
σ
∞
−∞
∞∗
−∞
∞∞ ∗
−∞ −∞
−−
=


−−
⋅

 −−

= ⋅
 

−−
⋅ ⋅⋅
=
∫
∫
∫∫
( )
2
22 2
2
2 22
2
2 22
22
22
exp(())cos (2)
cos(4)1
exp(())2
2
1exp(()) cos(4)
22
exp(())
1exp( 4)cos(4)1
22
t ffd
ff
tf d
ft ffd
t fd
fft
τπτ τ
π
πτ
στ τ
π
στπτ τ
π
ττ
σ ππ
π
∞
−∞
∞
−∞
∞
−∞
∞
−∞
 −−


 +

=−− ⋅
 




= ⋅−−⋅
 
 

+ −−

=⋅− +
∫
∫
∫
∫
(5)
Similarly, the imaginary part Im[( ,)]
n
S tf follows the
Gaussian distribution with
2
Im[(,)](0,( ))
nI
S tfNt σ 
,
where
( )
22 2
1
( )1exp(4)cos(4)
22
I
f
t ft σ σππ
π
= ⋅−− (6 )
In Equation (5) and Equation (6), the constant term,
2
exp( 4)7.1572e-18 π −≈
, is of very small value which
can approximately equal to zero, thus
(, )
n
Stf
can be
regarded as having identically distributed real and im-
aginary parts, that is,
Re[( ,)]
n
Stf
and
Im[( ,)]
n
Stf
2
1
(0, )
22
f
N σπ ⋅
.
Step.2: Derive the expression of the average S-spec-
trum of
()nt
,
2
(, )
n
ES tf


, and Prove that
Re[( ,)]
n
NSt f
and
Im[( ,)]
n
NSt f
follow identical
standard normal distribution.
The normalized S-spectrum of
()nt
can be written as
22
2
22
22
Re[(, )]Im[(,)]
(, )2(,)(, )
Re[( ,)]Im[( ,)]
nn
n
nn
nn
S tfS tf
NSt fE S tfE Stf
NSt fNSt f


=⋅+





= +
(7)
Since the average S-spectrum of
()nt
,
2
(, )
n
ES tf


, is given by
2
121
21 212
2
(,)[()()]( ,)
(,)exp( 2())
2
n
E S tfEnnwtf
wt ffjdd
f
τττ
τπ τ τττ
σ
π
∗
∞

= −

⋅−− −
=
∫∫
(8)
then the distribution of
Re[( ,)]
n
NSt f
and
Im[( ,)]
n
NSt f
can be obtained as
Re[(,)] ~(0,1);Im[(,)] ~(0,1)
nn
NSt fNNSt fN
(9)
Step.3: Prove that
Re[( ,)]
n
NSt f
and
Im[( ,)]
n
NSt f
are independent.
To determine the distribution of
2
(, )
n
NSt f
, the cor-
relation of
Re[( ,)]
n
NSt f
and
Im[( ,)]
n
NSt f
need to
be analyzed. The correlation function is
{ }
121222
11
12
2
22
22 12 12
2222
12
( ,)Re[( ,)]Im[(,)]
()
2[ ()()]exp2
()
expcos(2)sin(2)
2
() ()
2 expexp
22
cos(2 )
RIn n
RttENStfNStf
fft
En n
ft ffdd
fft ft
f
τ
ττ
σπ
τπτπτ ττ
ττ
π
πτ
∞∞ ∗
−∞ −∞
∞
−∞
= ⋅

−−
= ⋅


−−
⋅ ⋅⋅


 
−− −−
=⋅⋅
 
 
⋅⋅
∫∫
∫
( )
( )
( ) ( )
()() ( )
( )
2222
12
22 22
121 2
22
212 12
212
sin(2 )
() ()
expexpsin 4
22
exp2 2
2
2exp 4exp4
() 1exp(4) expexp2()
24
exp 2
fd
fft ftfd
ffttt t
jjfjf d
ft tjftt
j
ftt
f
πτ τ
ττ
πτ τ
π
ττ
π
πτπτ τ
ππ
τ
π
∞
−∞
∞
−∞
 
−− −−
= ⋅⋅
 
 

−
=−++ +


⋅ −−

−−
=⋅− ⋅⋅+


+
⋅⋅− −
∫
∫
( )
( )
2
22
212 12
2
212
22
212 12
2
() 1exp(4) expexp2()
24
2
exp 2
()
exp(4) expsin2()0
4
jd
f
ft tjft t
j
ftt
f jd
f
ft tftt
πτ
ππ
π
ττ
π
ππ
∞
−∞
∞
−∞




+
 






−−
−⋅ −⋅⋅−+




 +

⋅⋅− −−
 


 


−−
= −⋅⋅+≈


∫
∫
(10)

Characteristic Analysis of White Gaussian Noise in S-Transformation Domain
OPEN ACCESS JCC
22
Since both
Re[( ,)]
n
NSt f
and
Im[( ,)]
n
NSt f
follow
Gaussian distribution, Equation (10) means they are inde-
pendent. This concludes the proof that (, )
n
NSt f has
independent and identical distributed real and imaginary
parts of standard normal distribution, thus
2
(, )
n
NSt f
follows
2
χ
distribution with two degrees of freedom.
3. Numerical Simulations
In this section, Monte Carlo methods are used to demon-
strate the rationalities of above derivations. The variance
of WGN is set to be zero mean and
2
0.2 σ =
with 512
data points. The results are shown in Table 1, where the
theoretical values
2
()n
α
χ
are obtained by
2
χ
distribu-
tion table according to
{ }
22
() ()Pn n
α
χχ α >=
,
n
is
the degree of freedom,
k
is the times of Monte Carlo
methods and the simulation results are obtained by
k
realizations.
A good agreement between the theoretical values and
the simulation results can be observed. And as the times
of Monte Carlo experiments increase, the simulation re-
sults become closer to their theoretical values. Hence, we
have proved our proposition and obtained the distribution
of WGN in S transformation domain.
4. Signal Detection in ST Domain
In this section, the task of ST based detector is to provide
time -varying information in addition to detecting whe-
ther a transient signal is present or absent. We use the
concept of frame detection which is similar to the com-
mon method in voice activity detection (VAD) and no
cumulation operator is used. The time slice of S-spec-
trum is employed as the frame and the decision function
is
0
1
:()()
:()() ()
Hxt ntl
Hxtst ntl
= <Γ

= +≥Γ

(11)
where
()xt
is the observed signal,
()st
is the signal to
be detected and
()nt
is WGN at the time
t
(also
t
the frame index).
Γ
is the detection threshold and its
value can be calculated as
{ }
2
1(, )
2n
ES tf
f
γ
Γ= ⋅
(12)
where the value of
γ
can be determined by 2
χ
distri-
bution table according to the specific false alarm proba-
bility
FA
P and the value of
{ }
2
(, )
n
E S tf
can be es-
timated under the assumption that the initialization of
()xt
is the noise only. The detection statistic can be
expressed as
( )
2
max()
xt
lSf f=
(13 )
where
2
()
xt
Sf
is the time slice of
2
(, )
x
S tf
at the
time
t
. The constant-false-alarm-rate(CFAR) cr iterion
is employed in our detector. The probability of detection
D
P
is used as the performance variable and its value can
be numerically expressed as
H1|H1 H1
1
(1 /)()
k
Di
P kNN
=
=∑
(14)
where
k
is the time of Monte Carlo realizations,
H1
N
is the number of the transient signal frames and
H1|H1
N
is that of the correct detection frames.
In the analysis, a transient sinusoid signal under WGN
environment is used to illustrate the performance of sig-
nal detection in ST domain. The simulation signal is of
500 data points with 150 points pure noise at the begin-
ning segment and the end segment, respectively.
Figure 1 shows an example of frame detection at
H1|H1
N
. In this simulation, 4 different frames are selected
and it is obvious that the frame at
175t=
is the signal
frame while others are noise ones. In Figure 2, the de-
tector performance is shown in terms of
D
P
versus SNR
curves according to three different
FA
P
under CFAR
criteria. The results show that the proposed detector can
achieve reliable detection at the noise level higher than
0dB
.
Figure 3 depicts the performance comparison of pro-
posed detector with the same frame detector which uses
STFT instead of ST. The threshold corresponding to spe-
cific
FA
P
of STFT based detector is obtained by Monte
Carlo method of 10000 realizations. The sup eriority of
frame detection is to provide time-varying information.
Thus in Figure 4, the initiation time detection result of
the transient sinusoid signal is shown under the error
tolerance of 1 frame. The simulation result essentially
means that this linear time-frequency representation
could be potentially used for accurate estimation of the
time -varying parameters for nonstationary signals.
5. Conclusion
In this paper, the characteristic analysis of white Gaussian
Table 1. Simulation results of
2
()
α
χn
according to
{ }
()()
22
α
=Pn nα> χχ
by
k
realizations.
α
0.025 0.05 0.1 0.25 0.75
theoretical 7.378 5.991 4.605 2.773 0.575
1000k=
7.4969 6.0005 4.6058 2.7514 0.5640
10000k=
7.3757 5.9915 4.6036 2.7628 0.5732
α
0.90 0.95 0.975 0.99 0.995
theoretical 0.211 0.103 0.051 0.020 0.010
1000k=
0.2079 0.1006 0.0500 0.0218 0.0108
10000k=
0.2096 0.1025 0.0504 0.0203 0.0102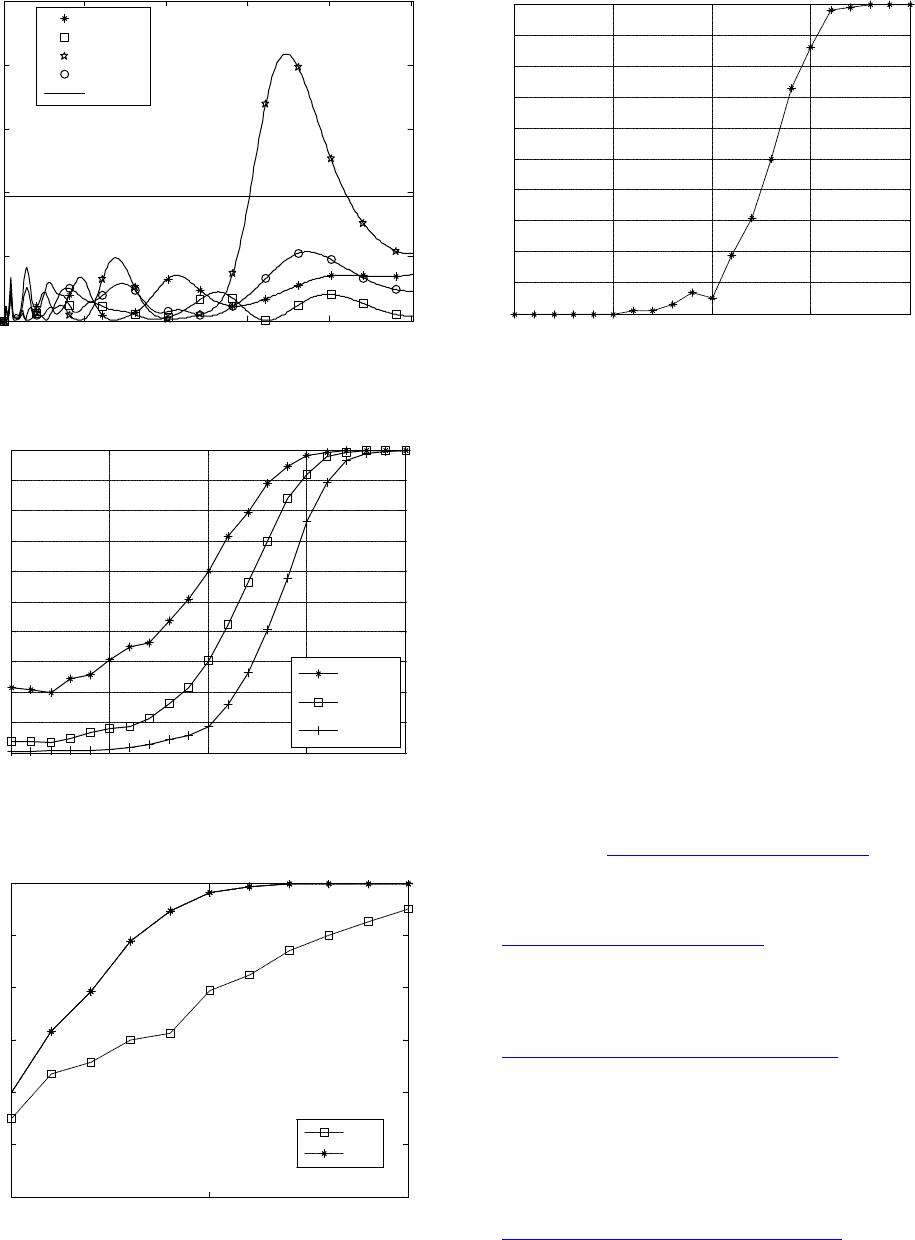

Characteristic Analysis of White Gaussian Noise in S-Transformation Domain
OPEN ACCESS JCC
23
Figure 1. Frame detection results at four different indexes
under the noise level of
SNR= 0 dB
.
Figure 2.
SNR -
D
P
curve for presented detector under
three different false alarm probabilities.
Figure 3. Detection performance of frame detector based on
ST and STFT at
-2
= 10
FA
P
.
Figure 4. Initiation time detection results of transient sinu-
soid signals using frame detection.
noise in S transformation domain has been performed.
Accurate distribution of WGN has been analytically de-
rived and been further verified through numerical analy-
sis. This result could be useful in signal detection and
ST-based signal processing scheme.
Acknowledgments
This research was supported in part by a National Natural
Science Foundation of China (61301286, 61201287) and
a Fundamental Research Funds for the Central Universi-
ties (K50511020022).
REFERENCES
[1] R. G. Stockwell, L. Mansinha and R. P. Lowe, “Localiza-
tion of the Complex Spectrum: The S-Transform,” IEEE
Transactions on Signal Processing, Vol. 44, No. 4, 1996,
pp. 998-1001. http://dx.doi.org/10.1109/78.492555
[2] C. R. Pinnegar and L. Mansinha, “The S-Transform with
Windows of Arbitrary and Varying Shape,” Geophysics,
Vol. 68, No. 1, 2003, pp. 381-385 .
http://dx.doi.org/10.1190/1.1543223
[3] A. G. Rehorn, E. Sejdic and J. Jiang, “Fault Diagnosis in
Machine Tools Using Selective Regional Correlation,”
Mechanical Systems and Signal Processing, Vol. 20, No.
5, 2006, pp. 1221-1238.
http://dx.doi.org/10.1016/j.ymssp.2005.01.010
[4] G. Livanos, N. Ranganathan and J. Jiang, “Heart Sound
Analysis Using the S-Transform,” Proceedings of Com-
puters in Cardiology, Cambridge, 24-27 September 2000,
587-590.
[5] C. R. Pinnegar and L. Mansinha, “The Bi-Gaussian S-
Transform,” SIAM: SIAM Journal on Scientific Compu-
ting, Vol. 24, No. 5, 2003, pp. 1678-1692.
http://dx.doi.org/10.1137/S1064827500369803
[6] C.R. Pinnegar, L. Mansinha, “Time-Local Fourier Analy-
sis with a Scalable, Phase-Modulated Analyzing Function:
0.2 0.40.60.81
0
5
10
15
20
25
Normalized Frequency
A m pl i t ude
t =100
t =125
t =175
t =400
Threshol d
-15 -10 -5 05
0
0. 1
0. 2
0. 3
0. 4
0. 5
0. 6
0. 7
0. 8
0. 9
1
S NR( d B)
P
d
P
FA
= 10
-2
P
FA
= 10
-3
P
FA
= 10
-4
-5 0 5
0. 4
0. 5
0. 6
0. 7
0. 8
0. 9
1
SNR(dB)
P
d
STFT
ST
-15 -10 -505
0
0. 1
0. 2
0. 3
0. 4
0. 5
0. 6
0. 7
0. 8
0. 9
1
S NR(d B )
P
d

Characteristic Analysis of White Gaussian Noise in S-Transformation Domain
OPEN ACCESS JCC
24
The S-Transform with a Complex Window,” Signal
Process, Vol. 84, No. 7, 2004, pp. 1167-1176.
http://dx.doi.org/10.1016/j.sigpro.2004.03.015
[7] M. Schimmel and J. Gallart, “The Inverse S-Transform in
Filters with T ime-Frequency Localization,” IEEE Trans-
actions on Signal Process, Vol. 53, No. 11, 2005, pp.
4417-4422. http://dx.doi.org/10.1109/TSP.2005.857065
[8] C. Simon, S. Ventosa, M. Schimmel, A. Heldring, J. J.
Dañobeitia, J. Gallart and A. Mànuel, “The S-Transform
and Its Inverses: Side Effects of Discretizing and Filter-
ing,” IEEE Transactions on Signal Processing, Vol. 55,
No. 10, 2007, pp. 4928-4937.
http://dx.doi.org/10.1109/TSP.2007.897893
[9] E. Sejdic, L. Stankovic, M. Dakovic and J. Jiang, “In-
stantaneous Frequency Estimation Using the S-Trans-
form,” IEEE Signal Processing Letters, Vol. 15, 2008, pp.
309-312. http://dx.doi.org/10.1109/LSP.2008.917014
[10] E. Sejdic and J. Jiang, “Selective Regional Correlation for
Pattern Recognition,” IEEE Transactions on Systems,
Man, and Cybernetics, Vol. 37, No. 1, 2007, pp. 82-93.
[11] J. H. Gao, W. S. Man and S. M. Chen, “Recognition of
Signals from Colored Noise Background in Generalized
S-Transformation Domain,” Chinese Journal of Geo-
physics, Vol. 47, No. 5, 2004, pp. 869-875.
http://dx.doi.org/10.1002/cjg2.576