 Journal of Applied Mathematics and Physics, 2014, 2, 1-7 Published Online January 2014 (http://www.scirp.org/journal/jamp) http://dx.doi.org/10.4236/jamp.2014.21001 OPEN ACCESS JAMP Higher-Order Numeric Solutions for Nonlinear Systems Based on the Modified Decomposition Method Junsheng Duan School of Sciences, Shanghai Institute of Technology, Shanghai, China Email: dua njssdu@sina.com, duanjs@sit.edu.cn Received July 2013 ABSTRACT Higher-order numeric solutions for nonlinear differential equations based on the Rach-Adomian-Meyers mod- ified decomposition method are designed in this work. The presented one-step numeric algorithm has a high effi- ciency due to the new, efficient algorithms of the Adomian polynomials, and it enables us to easily generate a higher-order numeric scheme such as a 10th-order scheme, while for the Runge-Kutta method, there is no gen- eral procedure to generate higher-order numeric solutions. Finally, the method is demonstrated by using the Duffing equation and the pendulum equation. KEYWORDS Adomian Polynomials; Modified Decomposition Method; Adomian-Rach Theorem; Nonlinear Differential Equations; Numeric Solution 1. Introduction The Adomian decomposition method (ADM) [1-4] is a practical technology for solving linear or nonlinear or- dinary differential equations, partial differential equations, integral equations, etc. The ADM provides an effi- cient analytic approximate solution of nonlinear equations, which model real-world applications in engineering and the applied sciences. The Adomian decomposition series has been shown to be equivalent to a Banach-space analog of the Taylor series expansion about the initial solution component function, instead of the classic Taylor series expansion about a constant that is the initial point [5]. The ADM decomposes the pre-existent, unique, analytic solution into a series 0 , n n ∞ = =∑ (1) and decomposes the nonlinearity into the series of the Adomian polynomials (2) where the Adomian polynomials depend on the solution component functions and are de- fined by the formula [3] 00 1() ,0. ! nk nk nk d Afu n nd λ λ λ ∞ == = ≥ ∑ (3) For convenient reference, we list the first five Adomian polynomials 2 1 2 02 0 '( )''( ). 2! u Afuufu= +  J. S. DUAN OPEN ACCESS JAMP 3 1 3030 120 '( )''( )'''( ). 3! u Afuuf uuufu=++ (4) 212 1 40 401300 '( )''( )()'''( )( ). 2!2! 4! uuu u Afu ufuuufufu = ++++ Some algorithms for symbolic programming have since been devised to efficiently generate the Adomian po- lynomials quickly to high orders, such as in [5-10]. Rach’s Rule for the Adomian polynomials reads () 0 1 ( ),1. nkk nn k AfuC n = = ≥ ∑ (4) where the coefficients are the sums of all possible products of components from whose subscripts sum to , divided by the factorial of the number of repeated subscripts [6]. New, more efficient algorithms and subroutines in MATHEMATICA for fast generation of the one-variable and multi-variable Adomian polynomials to high orders have been provided in [8-10]. Here we list Corollary 3 algorithm [10] for the one-variable Adomian polynomials. Corollary 3 algorithm [10]: For , (5) For , 1 11 0 1( 1). nk kk nj nj j Cj uC n −− + −− = = + ∑ (6) Then the Adomian polynomials are given by the formula The recurrence procedure for does not involve the differentiation operator, only requires the operations of addition and multiplication, which is eminently convenient for computer algebra systems. In 1992, Rach, Adomian and Meyers [11] proposed a modified decomposition method based on the nonlinear transformation of series by the Adomian-Rach theorem [12,13]: If then 0 0 (())( ), n n n fuxA xx ∞ = = − ∑ (7) where are the Adomian polynomials in terms of the solution coefficients. The Rach-Adomian-Meyers modified decomposition method [11] combines the power series solution and the Ado mia n -Rach theorem [12,13], and has been efficiently applied to solve various nonlinear models [2,14-16]. In this work, higher-order numeric one-step methods are designed for solving nonlinear differential equations based on the Rach-Adomian-Meyers modified decomposition method [11] and the previous research [17]. In the next section, we develop the numeric solution based on the modified decomposition method for nonli- near second-order differential equations, and demonstrate its application. 2. Higher-Order Numeric Solutions Based on the Modified Decomposition Method We consider the IVP for the second-order ODE 2 2()() ()()( )(), d udu ttuttf ugt dt dt αβ γ ++ += (8) (9) where are specified bounded, analytic functions, and is an analytic nonli-  J. S. DUAN OPEN ACCESS JAMP 3 near operator. The modified decomposition method supposes an analytic solution (10) Then the functions are decomposed into the Taylor expansions (11) (12) (13) (14) and the analytic nonlinearity is decomposed into the Taylor series (15) where the coefficients are the Adomian polynomials in terms of the solution coefficients due to the Adomian-Rach theorem [12,13]. Substituting Equation s (10)-(15) in Equations (8), regrouping terms, equating the coefficients of like powers of 0 tt−, and using the initial condition we obtain the recurrence scheme for the solution coefficients 21 0 1[((1 ))], ( 1)(2) m mmlmllmllml l agm laaA mm α βγ ++− − − = =− +−+ + ++ ∑ (16) where and the are the Adomian polynomials in terms of the coefficients for the nonlinear function . In particular, if , and are constants, then the recurrence formula becomes 21 1[( 1)],0. ( 1)(2) mmm mm agmaaAm mm α βγ ++ =−+− −≥ ++ (17) Further if is also a constant, then the recurrence formula becomes 2 100 1[ ], 2 aga aA αβγ =−− − 21 1[( 1)],1. ( 1)(2) mm mm amaaAm mm α βγ ++ − =+ ++≥ ++ (18) We denote the (n + 1)-term approximation of the solution as 1 0010 0 (,,,)() . nm nm m tt C Catt φ + = = − ∑ (19) We regard as three parameters, and generate the numeric solutions by using the (n + 1)-term ap- proximation . Partition the interval into . Here we consider an equal step-size partition with . The numeric solution generated by is of order n. We denote the nth-order numeric solution by , k = 0, 1, …, N. The one-step recurrence scheme is as follows:  J. S. DUAN OPEN ACCESS JAMP 111 1 ( 1) 112 (, ,,) , nn kn kkkk n n km kk m m utt uu uuha h φ <> <> +−− − <> − −− = = =++ ∑ 111 1 ( 1)1 12 (, ,,) , k n knkk k tt nkm km m d utt uu dt uma h φ <> +−− − = −− − = = =+ ∑ k = 1, 2, ···, N, where are the in (16), and for k = 2, ···, N, , , are determined by a recursion similar to (16) with and . Example 1. Consider the IVP for the Duffing equation 23 2 d2sinsin 2, d uuut t t−+ =− The IVP has the exact solution The Adomian polynomials for the nonlinearity are 22 2 4120201304 3 3 63,Aaa aaaaa aa=++ + The 8th-order numeric solutions on the interval [0,45] are plotted in Figure 1 with the step-size h = 0.5. The numeric solution is suitable for a larger domain as the order increases. Example 2. Consider the IVP for the pendulum equation 2 2 25sin0, (0)0,'(0)9. du uu u dt +=== The exact solution can be expressed in terms of a Jacobi elliptic function as *9 81 ()2arcsin(sn(5 ,)). 10 100 ut t= The Adomian polynomials in terms of the decomposition coefficients for the sinusoidal nonlinearity are Figure 1. The exact solution (solid line) and the 8th-order numeric solution on [0,45] with h = 0.5 (dots). 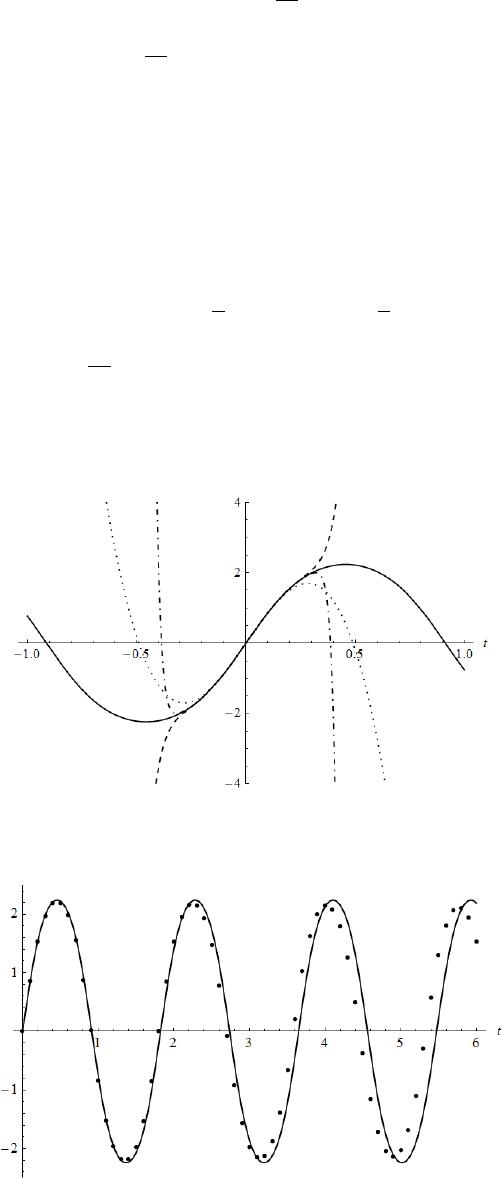 J. S. DUAN OPEN ACCESS JAMP 5 2 1 22 00 cossin , 2 a Aa aa= − 3 1 30 12030 cossincos , 6 a Aaaaaaa=−− − Using the initial conditions, the coefficients of solution series are calculated to be 0123 45 0,9,0,75 /2, 0,795 / 4,. aaaa aa ==== − = = The 5-term, 10-term and 20-term approximations are plotted in Figure 2. It is shown that the decomposition solution has a radius of convergence of more than 0.2. The 5-term approximation under the general initial conditions are calculated to be 23 5001 01000100 42 0 001 11 (,,,)()()sin()()cos() 26 1()sin()(cos()). 24 ttCCCCttttCCttC ttCC C φ γγ γγ =+ −−−−− +− + The 4th-order and 5th-order numeric solutions on the interval [0,6] with h = 0.1 are plotted in Figures 3 and 4, respectively. The 9th-order numeric solutions on the interval [0,10] with are plotted in F igure 5. We observe that the higher-order numeric solutions permit a larger step-size, and enlarge the effective region. Figure 2. The exact solution (solid line), the 5-term approximation (dot line), the 10-term appro- ximation (dash line) and the 20-term approximation (dot-dash line). Figure 3. The exact solution (solid line) and the 4th-order numeric solution on [0,6] with h = 0.1 (dots). 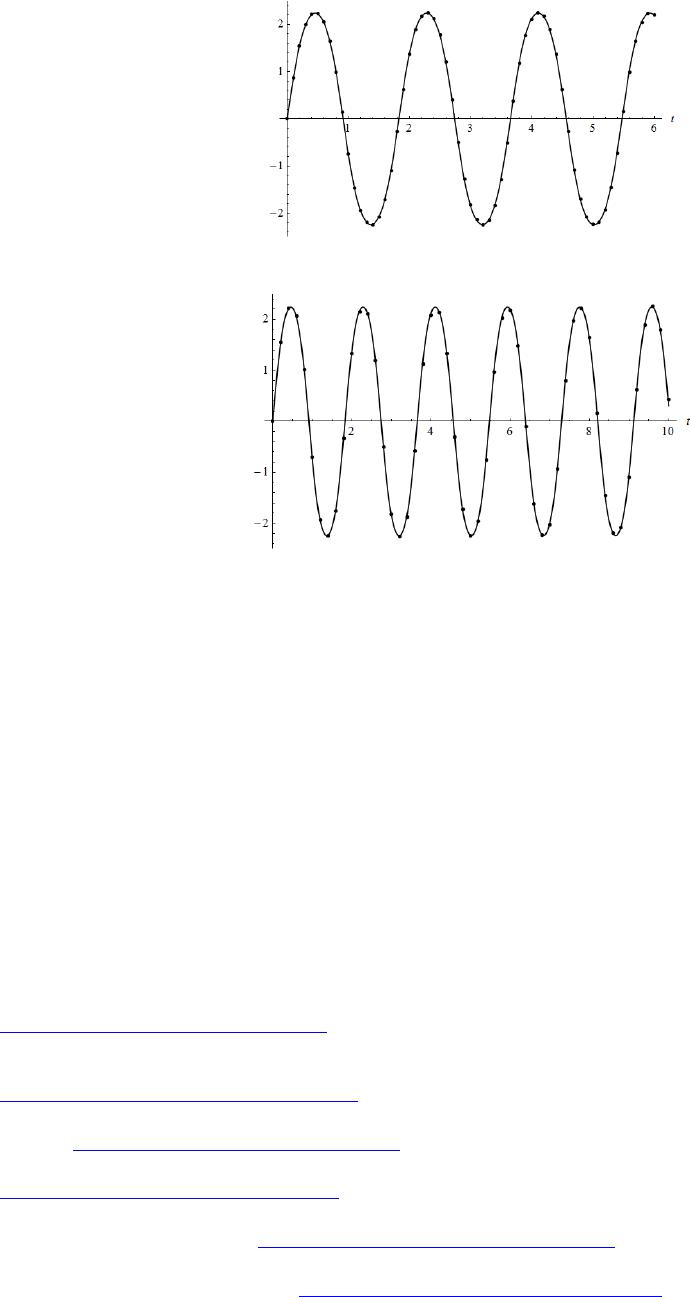 J. S. DUAN OPEN ACCESS JAMP Figure 4. The exact solution (solid line) and the 5th-order numeric solution on [0,6] with h = 0.1 (dots). Figure 5. The exact solution (solid line) and the 9th-order numeric solution on [0,10] with h = 0.2 (dots). 3. Conclusions We have developed higher-order numeric solutions for nonlinear differential equations based on the Rach- Ado mia n -Meyers modified decomposition method. Due to the new, efficient algorithms of the Adomian poly- nomials, the one-step numeric algorithm has a high efficiency, and permits us to easily generate a higher-order numeric scheme such as a 10th-order scheme, while for the Runge-Kutta method, there is no general procedure to generate higher-order numeric solutions. We demonstrated the presented numeric method by two nonlinear physical models. Acknowledgements This work was supported by the NNSF of China (11201308) and the Innovation Program of Shanghai Municipal Education Commission (14ZZ161). REFERENCES [1] G. Adomian, “Nonlinear Stochastic Operator Equations,” Academic, Orlando, 1986. [2] G. Adomian, “Solving Frontier Problems of Physics: The Decomposition Method,” Kluwer Academic, Dordrecht, 1994. http://dx.doi.org/10.1007/978-94-015-8289-6 [3] G. Adomian and R. Rach, “Inversion of Nonlinear Stochastic Operators,” Journal of Mathematical Analysis and Applications, Vol. 91, 1983, pp. 39-46. http://dx.doi.org/10.1016/0022-247X(83)90090-2 [4] A. M. Wazwaz, “Partial Differential Equations and Solitary Waves Theory,” Higher Education and Springer, Beijing and Ber- lin, 2009. http://dx.doi.org/10.1007/978-3-642-00251-9 [5] R. Rach, “A New Definition of the Adomian Polynomials,” Kybernetes, Vol. 37, 2008, pp. 910-955. http://dx.doi.org/10.1108/03684920810884342 [6] R. Rach, “A Convenient Computational Form for the Adomian Polynomials,” Journal of Mathematical Analysis and Applica- tions, Vol. 102, 1984, pp. 415-419. http://dx.doi.org/10.1016/0022-247X(84)90181-1 [7] A. M. Wazwaz, “A New Algorithm for Calculating Adomian Polynomials for Nonlinear Operators,” Applied Mathematics and Computation, Vol. 111, 2000, pp. 53-69. http://dx.doi.org/10.1016/S0096-3003(99)00063-6  J. S. DUAN OPEN ACCESS JAMP 7 [8] J. S. Duan, “Recurrence Triangle for Adomian Polynomials,” Applied Mathematics and Computation, Vol. 216, 2010, pp. 1235-1241. http://dx.doi.org/10.1016/j.amc.2010.02.015 [9] J. S. Duan, “An Efficient Algorithm for the Multivariable Adomian Polynomials,” Applied Mathematics and Computation, Vol. 217, 2010, pp. 2456-2467. http://dx.doi.org/10.1016/j.amc.2010.07.046 [10] J. S. Duan, “Convenient Analytic Recurrence Algorithms for the Adomian Polynomials,” Applied Mathematics and Computa- tion, Vol. 217, 2011, pp. 6337-6348. http://dx.doi.org/10.1016/j.amc.2011.01.007 [11] R. Rach, G. Adomian and R. E. Meyers, “A modified Decomposition,” Computers & Mathematics with Applications, Vol. 23, 1992, pp. 17-23. http://dx.doi.org/10.1016/0898-1221(92)90076-T [12] G. Adomian and R. Rach, “Transformation of Series,” Applied Mathematics Letters, Vol. 4, 1991, pp. 69-71. http://dx.doi.org/10.1016/0893-9659(91)90058-4 [13] G. Adomian and R. Rach, “Nonlinear Transformation of Series—Part II,” Computers & Mathematics with Applications, Vol. 23, 1992, pp. 79-83. http://dx.doi.org/10.1016/0898-1221(92)90058-P [14] G. Adomian and R. Rach, “Modified Decomposition Solution of Linear and Nonlinear Boundary-Value Problems,” Founda- tions of Physics Letters, Vol. 23, 1994, pp. 615-619. http://dx.doi.org/10.1016/0362-546X(94)90240-2 [15] G. Adomian, R. Rach and N. T. Shawagfeh, “On the Analytic Solution of the Lane-Emden Equation,” Foundations of Physics Letters, Vol. 8, 1995, pp. 161-181. http://dx.doi.org/10.1007/BF02187585 [16] J. C. Hsu, H. Y. Lai and C. K. Chen, “An Innovative Eigenvalue Problem Solver for Free Vibration of Uniform Timoshenko Beams by Using the Adomian Modified Decomposition Method,” Journal of Sound Vibration, Vol. 325, 2009, pp. 451-470. http://dx.doi.org/10.1016/j.jsv.2009.03.015 [17] G. Adomian, R. C. Rach and R. E. Meyers, “Numerical Integration, Analytic Continuation, and Decomposition,” Applied Ma- thematics and Computation, Vol. 88, 1997, pp. 95-116. http://dx.doi.org/10.1016/S0096-3003(96)00052-5
|