Journal of Service Science and Management, 2011, 4, 8-14
doi:10.4236/jssm.2011.41002 Published Online March 2011 (http://www.SciRP.org/journal/jssm)
Characterizing and Modeling the Structure of
Competition Networks*
Bo Yang, Hecheng Wang
School of Management, Hangzhou Dianzi University, Hangzhou, China.
Received November 1st, 2010; revised December 15th, 2010; accepted December 19th, 2010.
ABSTRACT
Not similar with the current interest on collaboration networks research, the focus in this paper is competition networks.
The topology of a firm competition network has been investigated empirically and theoretically. We have found that
four fundamental characteristics emerge simultaneously in the competition network, including hierarchical modularity,
positive degree correlation, power-law degree distribution and self-similarity. The theoretical model we proposed can
predict these structural patterns successfully. The obtained results are significant for further network analysis of the
omnipresent competitive phenomena.
Keywords: Firm Competition, Structural Embeddedness, Complex Networks
1. Introduction
The last few years have witnessed a tremendous activity
devoted to the characterization and understanding of
networked systems. The focus is shifting away from the
analysis of single small networks and the properties of
individual vertex or edges to consideration of large-scale
statistical properties of complex networks [1-3]. Espe-
cially, some researches have concentrated on investigat-
ing network topology of social and economical systems,
using the complex network approach [4-6]. This trend
has naturally arisen and been reinforced because many
studies have demonstrated that network structure largely
affects economical dynamics taking place on the network
such as technological progress and diffusion of innova-
tions [7], and plays an important role in the optimization
of performance for economical systems [8].
Currently, the concern for network topology of real
socio-economical systems mainly focuses on collabora-
tion behaviors. Some examples widely studied involve
coauthorship networks [4], strategic partnership alliance
[5], supplier-customer networks [6], and etc. In these
collaboration networks, any two linked agents cooperate
towards their shared aim, for example coauthoring papers
and developing new products. Statistical properties of
this type of networks have been well analyzed.
However, in practice there exists different form of be-
haviors, i.e. competition behaviors, which are omnipres-
ent in real socio-economical systems, such as firms
competing for market share, employees competing for
promotion, and etc. Two linked agents in competition
networks compete but not collaborate towards their re-
spective aims. Current literature have provided little
knowledge about the topology of competition networks,
which are worthy of our concern. However, in the field
of sociology, two valuable papers [9] and [10] give us
insight into the question how to study the competitive
behaviors under network circumstances. The common
point of these two papers is that they adopt a structural
embeddedness perspective [11], which suggests that
competitors are embedded in a network of relationship
that influences their competitive behaviors. They argued
that the structural embeddedness of competitive dynam-
ics has not been studied explicitly. And they followed the
typical network approach, attempting to explore the re-
search question “How does the network of cooperative
linkages among competitors influence their competitive
behaviors towards each other?” It is certain that the use
of the network approach helps advance research in com-
petitive dynamics, and then helps develop a better under-
standing of competitive phenomena.
*Financial support was provided the National Natural Science Founda-
tion of China (No.70872028) and the Development Foundation o
f
Business Administration Discipline of Hangzhou Dianzi University (No
ZX100205004-3).
Different from the above-mentioned work, the aim of
this paper is to investigate the topology of competition

Characterizing and Modeling the Structure of Competition Networks9
network empirically and construct a theoretical model to
predict the structural patterns. In fact, it has been found
that many biological, social and technological empirical
networks may share some topological characteristics.
The researches in this field early focused on scale-free
degree distributions. However, further studies have ex-
tended to other properties, such as hierarchical modular-
ity, degree correlation and self-similarity, which have
been demonstrated to be fundamental and significant for
dynamic processes taking place on networks. Although
these characteristics are of much significance, more em-
pirical proofs in the further research should be found to
support their universality. In this paper, we will see that
the empirical firm competition network discussed below
exhibits power-law degree distribution, which has been
widely studied in current literature. Meanwhile, other
three characteristics are found to emerge in this firm
competition network, also.
On the other hand, motivated by empirical analysis,
research on theoretical network models to predict the
empirically-observed structural patterns has attracted a
large interest. There are Barabási-Albert model exhibit-
ing scale-free degree distribution [12], hierarchical net-
work model displaying scale-free and a high degree of
clustering [13], connecting nearest-neighbor model that
appears to display multiple features including scale-free
degree distribution, hierarchical modularity and positive
degree correlation [14], etc. In summary, the focus of
model research is shifting away from the analysis of sin-
gle structural properties to consideration of multiple
properties of networks. In this paper, we will also con-
struct a theoretical network model that can predict em-
pirically-observed structural patterns of the competition
network successfully.
The outline of this paper is as follows. In Section 2,
the topology of an empirically obtained firm competition
network is investigated first. Then in Section 3, a theo-
retical model is proposed. And, in Section 4, we give our
conclusions and point to directions for future research.
2. Empirical Analysis
2.1. Description of the Firm Competition
Network
Competition lies everywhere in real socio-economical
systems, between from individuals, firms to countries.
The attention of this paper is paid on the firm competi-
tion network, which is the representative form of compe-
tition networks in socio-economical systems. The em-
pirical network is constructed by analyzing data of firms
collected in a certain software industrial park in the south
of China. Vertices in this network represent firms in the
industrial park whose number is 574. Firms in the park
develop various application software products by offer-
ing technological support for customer needs. Their
products involve in the fields of network security, office
automation, communications, and etc. In reality, it is
known that firms compete by its products including tan-
gible products or intangible services, which accordingly
means that the more similar the products are, the more
firms compete. According to the above analysis, we can
construct the network as follows. For any two firms, if
their respective products are similar in function or cus-
tomer target and accordingly fall in the same product
category, there is competitive relationship between them
and thus an edge is constructed between these two firms.
In the limit of the length, the detail about how to classify
the involved products is not stated here. Notice that in the
research they have been professionally classified into 51
categories by a group of consultants. Therefore, we ob-
tain an undirected firm competition network that has
6597 edges. The network can be divided into 51 sub-
networks, in which all vertices connected to each other
obviously, according to the software product categories.
There are 479 firms among these 578 firms, which con-
strain to develop products in a single product category,
and thus the vertices representing them belong to one
single group only. On the other hand, other firms develop
products in several product categories, and thus the ver-
tices representing them belong to several groups simul-
taneously. The main network measurements often dis-
cussed in literature are presented briefly as follows.
1) Network density: The network density is defined as
the ratio between the number of actual links and the
maximum possible number of links. And the density is a
key network-level property that refers to the extent of
interconnection among the actors of the network. The
network density of this empirical network is 0.04, sparse
to some extent.
2) Vertex degree: The vertex degree is defined as the
number of edges connected to this vertex. And the aver-
age connectivity of vertices in the network is the mean
degree of all vertices. The average connectivity of verti-
ces in this network is 22.99 while the maximum degree is
144, meaning that an individual firm has about 30 com-
petitors in this industrial park on average and there exist
some firms which have 144 competitors at most.
3) Mean geodesic distance: According to [1], we use
the “harmonic mean” form to calculate this index. The
mean geodesic distance of this empirical network is 2.3,
which is indeed very small compared with the number of
vertices. It is certain that the so-called small world effect
exists in this empirical network.
4) Clustering coefficient: The clustering coefficient
measures the density of triangles in the network. In an-
other words, it measures the propensity for vertex pairs

C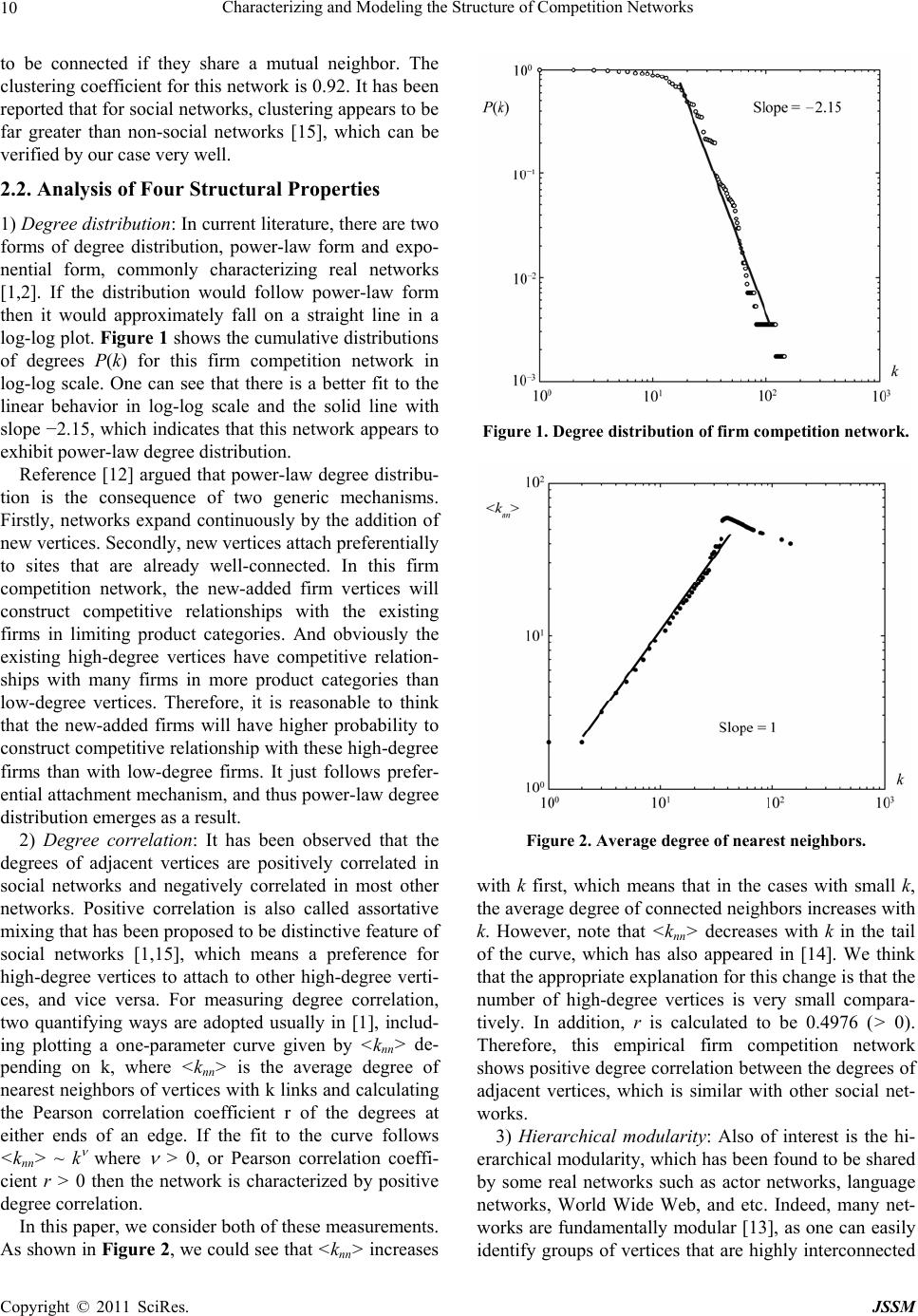haracterizing and Modeling the Structure of Competition Networks 10
to be connected if they share a mutual neighbor. The
clustering coefficient for this network is 0.92. It has been
reported that for social networks, clustering appears to be
far greater than non-social networks [15], which can be
verified by our case very well.
2.2. Analysis of Four Structural Properties
1) Degree distribution: In current literature, there are two
forms of degree distribution, power-law form and expo-
nential form, commonly characterizing real networks
[1,2]. If the distribution would follow power-law form
then it would approximately fall on a straight line in a
log-log plot. Figure 1 shows the cumulative distributions
of degrees P(k) for this firm competition network in
log-log scale. One can see that there is a better fit to the
linear behavior in log-log scale and the solid line with
slope −2.15, which indicates that this network appears to
exhibit power-law degree distribution.
Reference [12] argued that power-law degree distribu-
tion is the consequence of two generic mechanisms.
Firstly, networks expand continuously by the addition of
new vertices. Secondly, new vertices attach preferentially
to sites that are already well-connected. In this firm
competition network, the new-added firm vertices will
construct competitive relationships with the existing
firms in limiting product categories. And obviously the
existing high-degree vertices have competitive relation-
ships with many firms in more product categories than
low-degree vertices. Therefore, it is reasonable to think
that the new-added firms will have higher probability to
construct competitive relationship with these high-degree
firms than with low-degree firms. It just follows prefer-
ential attachment mechanism, and thus power-law degree
distribution emerges as a result.
2) Degree correlation: It has been observed that the
degrees of adjacent vertices are positively correlated in
social networks and negatively correlated in most other
networks. Positive correlation is also called assortative
mixing that has been proposed to be distinctive feature of
social networks [1,15], which means a preference for
high-degree vertices to attach to other high-degree verti-
ces, and vice versa. For measuring degree correlation,
two quantifying ways are adopted usually in [1], includ-
ing plotting a one-parameter curve given by <knn> de-
pending on k, where <knn> is the average degree of
nearest neighbors of vertices with k links and calculating
the Pearson correlation coefficient r of the degrees at
either ends of an edge. If the fit to the curve follows
<knn> ~ k

where  > 0, or Pearson correlation coeffi-
cient r > 0 then the network is characterized by positive
degree correlation.
In this paper, we consider both of these measurements.
As shown in Figure 2, we could see that <knn> increases
Figure 1. Degree distribution of firm competition network.
Figure 2. Average degree of nearest neighbors.
with k first, which means that in the cases with small k,
the average degree of connected neighbors increases with
k. However, note that <knn> decreases with k in the tail
of the curve, which has also appeared in [14]. We think
that the appropriate explanation for this change is that the
number of high-degree vertices is very small compara-
tively. In addition, r is calculated to be 0.4976 (> 0).
Therefore, this empirical firm competition network
shows positive degree correlation between the degrees of
adjacent vertices, which is similar with other social net-
works.
3) Hierarchical modularity: Also of interest is the hi-
erarchical modularity, which has been found to be shared
by some real networks such as actor networks, language
networks, World Wide Web, and etc. Indeed, many net-
works are fundamentally modular [13], as one can easily
identify groups of vertices that are highly interconnected

C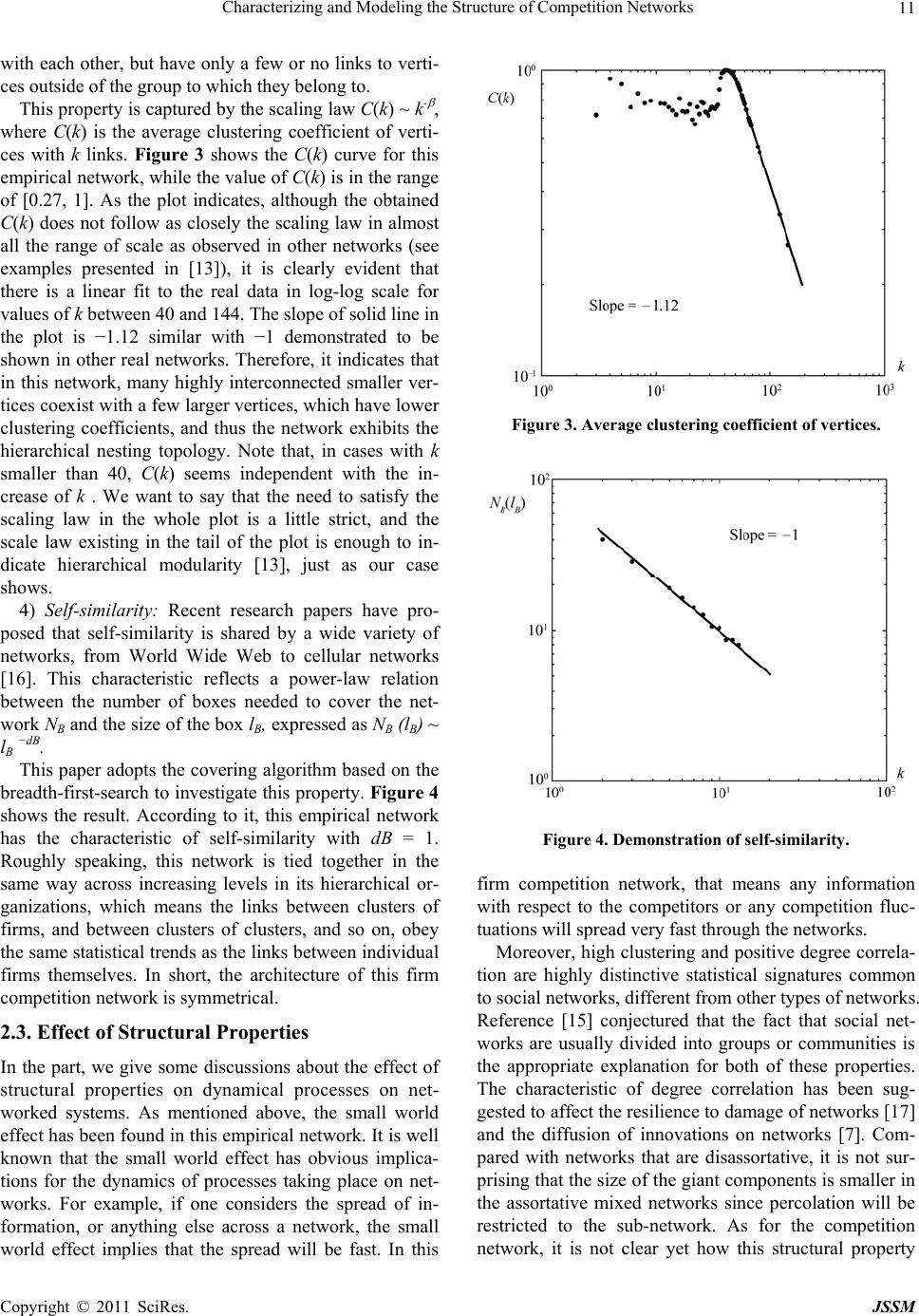haracterizing and Modeling the Structure of Competition Networks11
with each other, but have only a few or no links to verti-
ces outside of the group to which they belong to.
This property is captured by the scaling law C(k) ~ k-

,
where C(k) is the average clustering coefficient of verti-
ces with k links. Figure 3 shows the C(k) curve for this
empirical network, while the value of C(k) is in the range
of [0.27, 1]. As the plot indicates, although the obtained
C(k) does not follow as closely the scaling law in almost
all the range of scale as observed in other networks (see
examples presented in [13]), it is clearly evident that
there is a linear fit to the real data in log-log scale for
values of k between 40 and 144. The slope of solid line in
the plot is −1.12 similar with −1 demonstrated to be
shown in other real networks. Therefore, it indicates that
in this network, many highly interconnected smaller ver-
tices coexist with a few larger vertices, which have lower
clustering coefficients, and thus the network exhibits the
hierarchical nesting topology. Note that, in cases with k
smaller than 40, C(k) seems independent with the in-
crease of k . We want to say that the need to satisfy the
scaling law in the whole plot is a little strict, and the
scale law existing in the tail of the plot is enough to in-
dicate hierarchical modularity [13], just as our case
shows.
4) Self-similarity: Recent research papers have pro-
posed that self-similarity is shared by a wide variety of
networks, from World Wide Web to cellular networks
[16]. This characteristic reflects a power-law relation
between the number of boxes needed to cover the net-
work NB and the size of the box lB, expressed as NB (lB) ~
lB −dB.
This paper adopts the covering algorithm based on the
breadth-first-search to investigate this property. Figure 4
shows the result. According to it, this empirical network
has the characteristic of self-similarity with dB = 1.
Roughly speaking, this network is tied together in the
same way across increasing levels in its hierarchical or-
ganizations, which means the links between clusters of
firms, and between clusters of clusters, and so on, obey
the same statistical trends as the links between individual
firms themselves. In short, the architecture of this firm
competition network is symmetrical.
2.3. Effect of Structural Properties
In the part, we give some discussions about the effect of
structural properties on dynamical processes on net-
worked systems. As mentioned above, the small world
effect has been found in this empirical network. It is well
known that the small world effect has obvious implica-
tions for the dynamics of processes taking place on net-
works. For example, if one considers the spread of in-
formation, or anything else across a network, the small
world effect implies that the spread will be fast. In this
Figure 3. Average clustering coefficient of vertices.
Figure 4. Demonstration of self-similarity.
firm competition network, that means any information
with respect to the competitors or any competition fluc-
tuations will spread very fast through the networks.
Moreover, high clustering and positive degree correla-
tion are highly distinctive statistical signatures common
to social networks, different from other types of networks.
Reference [15] conjectured that the fact that social net-
works are usually divided into groups or communities is
the appropriate explanation for both of these properties.
The characteristic of degree correlation has been sug-
gested to affect the resilience to damage of networks [17]
and the diffusion of innovations on networks [7]. Com-
pared with networks that are disassortative, it is not sur-
prising that the size of the giant components is smaller in
the assortative mixed networks since percolation will be
restricted to the sub-network. As for the competition
network, it is not clear yet how this structural property

Characterizing and Modeling the Structure of Competition Networks 12
affects the competitive dynamics on it.
As for power-law degree distribution, the probability
of high degree vertices decays not so rapidly, compared
with the case with exponential degree distribution. It
means that there indeed exist a certain number of ex-
tremely high degree vertices, so-called hub vertices. Re-
lated to degree distribution is the property of resilience of
networks. In literature from different disciplines so far,
the importance of hub vertices has been mentioned fre-
quently. It has been observed that many networks with
power-law degree distribution are robust against random
vertex removal, but less robust to targeted removal of the
highest degree vertices. In this firm competition network,
the importance of high-degree firms is highlighted there-
fore, and the removal or any change of these types of
firms will have significant effects on the whole network.
There is little attention having been given to the effect
of hierarchical modularity and self-similarity on dy-
namical behaviors of networked systems yet. Reference
[15] have proposed that the presence of hierarchical
modularity reinterprets the role of the hubs in complex
networks, which are known to play a key role of increas-
ing robustness and spreading viruses for scale-free net-
works. In this firm competition network, the positions of
high-degree vertices, which full the structural holes
among communities, obviously have some important
implications for information spread. For self-similarity,
reference [18] has proposed that it can be used as a
benchmark for testing models of network structure,
which therefore is important to the research on dynamic
processes based on the network structural model.
3. Theoretical Model
3.1. Model of the Firm Competition Network
As mentioned above, the focus of network model research
is shifting away from the analysis of single structural
properties to consideration of multiple properties of net-
works. To the best of our knowledge, there is no existing
network model that can theoretically reproduce four char-
acteristics of the competitive network simultaneously al-
though they are proved to emerge at the same time.
Therefore there is a requirement to propose a theoretical
model that can reproduce them at the same time and pre-
dict the topology of firm competition network successfully,
which will full the gap of existing models to some extent.
As mentioned in the part of introduction, competition
behaviors are omnipresent behaviors, which could be
found everywhere. We found many valuable literatures
in the research field of competitive food web, studying
the structural properties of food webs and proposing sev-
eral theoretical network models [19,20]. Between the
competitions among species and the competitions among
firms, there indeed exists some essential similarity.
Drawing valuable ideas from this completely different
discipline, we form and describe our theoretical network
model as follows.
In fact, in firm competition networks, the features of
its developed products, such as the product function or
the customer target, can characterize each firm. And an
edge between two firms is constructed if their character-
istics are similar and thus two firms form competitive
relationship. It hints two possible factors affecting the
topology of the network. First is heterogeneity in vertices
characteristics. In fact, if all vertices characteristics are
completely homogeneous, that is, all firms in the real
system (such as in an industry or a park) produce the
similar products, then the corresponding network is fully
connected, which is not discussed in this paper. On the
other hand, in view of products features, there is a com-
peting range for each firm, for instance in reality the field
of e-commerce application platform or the field of enter-
prise management system. All firms in the system whose
developed products have the features falling in this range
are the competitors of this firm due to the similarity in
their products features. Other firms out of this range have
no direct competition with this firm. The ranges vary
depending on different products developed by firms,
which accordingly affect the connection of network.
Therefore, the theoretical model can be constructed as
follows. Given N vertices, each vertex i is assigned a
characteristic value xi that is drawn from a beta distribu-
tion


1,Beta

where

1, 


 quantifies the het-
erogeneity level in nodes’ characteristic values. Con-
cretely, the heterogeneity level is increasing as

de-
creases towards 1. Especially, when

= 1 all nodes’
characteristic values are drawn from the uniform distri-
bution. As mentioned above, in view of some practical
limits, the vertices would be constrained to compete with
vertices within a certain range. Expressed by formula, if
|(xi − xj)|≤ (ri + rj)/2 then vertex i and j are connected, or
else two vertices are not connected. Here, ri is assumed to
be a random variable from a beta distribution


Be 1,ta

where

represents the variability of ri. It is known that




11Ex


 for

~1,xBeta


and




11Er

 for

~1,rBeta


. In order to assure
the model-generated network’s average connectivity close
to the empirical network’s, we choose

and

in si-
mulation to satisfy

 
11 1   4C where the left
item is just




rEx E and C equals


21LN N

that is just the network density being the ratio between
the number of actual links and the possible number L


12NN in the empirical undirected network. By
adjusting the parameter

and

, we can find out the
optimal network that predicts those empirical character-
istics better than all other model-generated networks.

C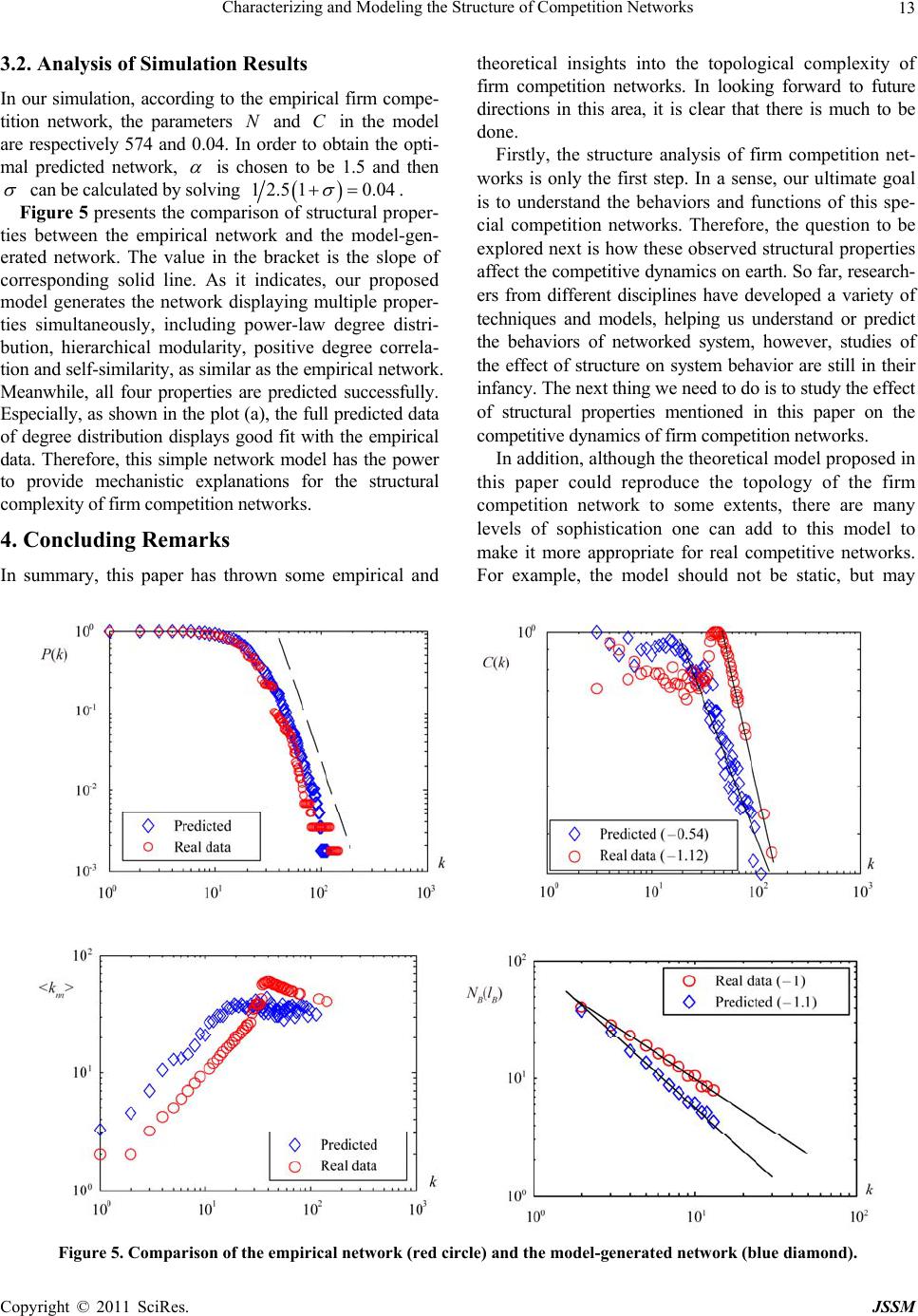haracterizing and Modeling the Structure of Competition Networks 13
3.2. Analysis of Simulation Results theoretical insights into the topological complexity of
firm competition networks. In looking forward to future
directions in this area, it is clear that there is much to be
done.
In our simulation, according to the empirical firm compe-
tition network, the parameters and in the model
are respectively 574 and 0.04. In order to obtain the opti-
mal predicted network,
N C

is chosen to be 1.5 and then

can be calculated by solving

1 2.5 10.04  .
Firstly, the structure analysis of firm competition net-
works is only the first step. In a sense, our ultimate goal
is to understand the behaviors and functions of this spe-
cial competition networks. Therefore, the question to be
explored next is how these observed structural properties
affect the competitive dynamics on earth. So far, research-
ers from different disciplines have developed a variety of
techniques and models, helping us understand or predict
the behaviors of networked system, however, studies of
the effect of structure on system behavior are still in their
infancy. The next thing we need to do is to study the effect
of structural properties mentioned in this paper on the
competitive dynamics of firm competition networks.
Figure 5 presents the comparison of structural proper-
ties between the empirical network and the model-gen-
erated network. The value in the bracket is the slope of
corresponding solid line. As it indicates, our proposed
model generates the network displaying multiple proper-
ties simultaneously, including power-law degree distri-
bution, hierarchical modularity, positive degree correla-
tion and self-similarity, as similar as the empirical network.
Meanwhile, all four properties are predicted successfully.
Especially, as shown in the plot (a), the full predicted data
of degree distribution displays good fit with the empirical
data. Therefore, this simple network model has the power
to provide mechanistic explanations for the structural
complexity of firm competition networks.
In addition, although the theoretical model proposed in
this paper could reproduce the topology of the firm
competition network to some extents, there are many
levels of sophistication one can add to this model to
make it more appropriate for real competitive networks.
For example, the model should not be static, but may
4. Concluding Remarks
In summary, this paper has thrown some empirical and
Figure 5. Comparison of the empirical network (red circle) and the model-generated network (blue diamond).

Characterizing and Modeling the Structure of Competition Networks 14
evolve over time with vertices or edges appearing or
disappearing, or values defined on them changing.
Moreover, in the future research, we can use this theo-
retical model as a research platform to explore a vast
variety of complex and poorly understood competitive
phenomena in the field of industry organization. For
example, how do the competition networks evolve? How
does the different position in the networks influence the
individual firm’s control ability of competition? How do
the fluctuations spread on the competition networks?
It is worthy to note that although the research in this
paper is constructed on the basis of firm competition
networks, it may be extended to the analysis of the gen-
eral competition systems. As mentioned above, competi-
tive phenomena are omnipresent in real socio-economi-
cal systems. We hope that our preliminary investigations
in the firm competition will stimulate other researchers to
pursue more extensions.
5. Acknowledgements
The authors would like to thank CHEN Xiao-rong for her
fruitful discussions during the development of this paper.
REFERENCES
[1] M. E. J. Newman, “The Structure and Function of Com-
plex Networks,” SIAM Review, Vol. 45, No. 2, 2003, pp.
167-256. doi:10.1137/S003614450342480
[2] R. Albert and A.-L. Barabasi, “Statistical Mechanics of
Complex Networks,” Reviews of Modern Physics, Vol. 74,
No. 1, 2002, pp. 47-97. doi:10.1103/RevModPhys.74.47
[3] D. J. Watts, “The “New” Science of Networks,” Annual
Review of Sociology, Vol. 30, 2004, pp. 243-270.
doi:10.1146/annurev.soc.30.020404.104342
[4] M. E. J. Newman, “The Structure of Scientific Collabora-
tion Networks”, Proceedings of the National Academy of
Sciences, USA, Vol. 98, No. 2, 2001, pp. 404-409.
doi:10.1073/pnas.021544898
[5] M. Riccaboni and F. Pammolli, “On Firm Growth in
Networks,” Research Policy, Vol. 31, No. 8-9, 2002, pp.
1405-1416. doi:10.1016/S0048-7333(02)00071-9
[6] M. Parhi, “Dynamics of Inter-Firm Linkages in Indian
Auto Component Industry: A Social Network Analysis,”
DRUID Winter Conference, Denmark, January 2005.
[7] X. Guardiola, A. Diaz-Guilera, C. J. Perez, A. Arenas and
M. Llas, “Modelling Diffusion of Innovations in a Social
Network,” Physical Review E, Vol. 66, No. 2, 2002.
doi:10.1103/PhysRevE.66.026121
[8] A. Arenas, A. Daz-Guilera, C. J. Prez and F. Vega-
Redondo, “Self-Organized Evolution in Socio-Economic
Environments,” Physical Review E, Vol. 61, No. 4, 2000,
pp. 3466-3469. doi:10.1103/PhysRevE.61.3466
[9] D. R. Gnyawali and R. Madhavan, “Cooperative Networks
and Competitive Dynamics: A Structural Embeddedness
Perspective,” Academy of Management review, Vol. 26,
No. 3, 2001, pp. 431-445. doi:10.2307/259186
[10] B. Uzzi, “Social Structure and Competition in Interfirm
Networks: The Paradox of Embeddedness,” Administra-
tive Science Quarterly, Vol. 42, No. 1, 1997, pp. 35-67.
doi:10.2307/2393808
[11] M. Granovetter, “Economic Action and Social Structure:
The Problem of Embeddedness,” American Journal of
Sociology, Vol. 91, No. 3, 1985, pp. 481-510.
doi:10.1086/228311
[12] A.-L. Barabasi and R. Albert, “Emergence of Scaling in
Random Networks.” Science, Vol. 286, No. 5439, 1999,
pp. 509-512. doi:10.1126/science.286.5439.509
[13] E. Ravasz and A.-L. Barabasi, “Hierarchical Organization
in Complex Networks,” Physical Review E, Vol. 67, No. 2,
2003, pp. 026112-1-7. doi:10.1103/PhysRevE.67.026112
[14] A. Vazquez, “Growing Network with Local Rules: Pref-
erential Attachment, Clustering Hierarchy, and Degree
Correlations,” Physical Review E, Vol. 67, No. 5, 2003,
056104. doi:10.1103/PhysRevE.67.056104
[15] M. E. J. Newman and J. Park, “Why Social Networks are
Different from Other Types of Networks,” Physical Re-
view E, Vol. 68, No. 3, 2003, 036112.
[16] C. Song, S. Havlin and H. A. Makse, “Self-Similarity of
Complex Networks,” Nature, Vol. 433, No. 7024, 2005,
pp. 392-395. doi:10.1038/nature03248
[17] A. Vazquez and Y. Moreno, “Resilience to Damage of
Graphs with Degree Correlations,” Physical Review E, Vol.
67, No. 1, 2003, 015101.
doi:10.1103/PhysRevE.67.015101
[18] S. H. Strogatz, “Romanesque Networks,” Nature, Vol.
433, No. 7024, 2005, pp. 365-366. doi:10.1038/433365a
[19] R. J. Williams and N. D. Martinez, “Simple Rules Yield
Complex Food Webs,” Nature, Vol. 404, No. 6774, 2000,
pp. 180-183. doi:10.1038/35004572
[20] N. Rooney, K. S. McCann and J. C. Moore, “A Land-
scape Theory for Food Web Architecture,” Ecology Let-
ters, Vol. 11, No. 8, 2008, pp. 867-881.
doi:10.1111/j.1461-0248.2008.01193.x