Materials Sciences and Applications, 2011, 2, 180-186
doi:10.4236/msa.2011.23022 Published Online March 2011 (http://www.SciRP.org/journal/msa)
The Modifications of Wagner’s Equation and
Electrochemistry for the 21st Century
Tomofumi Miyashita
Miyashita Clinic, Osaka, Japan.
Received January 4th, 2011; revised February 10th, 2011; accepted February 14th, 2011.
ABSTRACT
The use of samarium-doped ceria (SDC) electrolytes in SOFCs (solid oxide fuel cells) lowers the open circuit voltage
(OCV) below the Nernst voltage (Vth). The OCV is calculated with Wagner’s equation which is included in Nernst-
Planck equation. Considering the separation of Boltzmann distribution, the fundamental basis of this topic is discussed.
A constant voltage loss without leakage currents due to a mixed ionic and electronic conducting (MIEC) dense anode
was explained. Only carrier species having sufficient energy to overcome the activation energy can contribute to cur-
rent conduction, which is determined by incorporating a different constant in the definitions of chemical potential and
electrical potential. This difference explains the results using dense MIEC anodes. This topic is not an isolated and mi-
nor topic, but of vital importance to electrochemical engineering for the 21st Century.
Keywords: SOFC, Ceria, Open Circuit Voltage, Mixed Ionic and Electronic Conductors, Wagner’s Equation,
Boltzmann’s Distribution, Maxwell’s Demon
1. Introduction
Solid-oxide fuel cells (SOFCs) directly convert the che-
mical energy of fuel gases, such as hydrogen or methane,
into electrical energy. In SOFCs, a solid-oxide film is
used as the electrolyte. Oxygen ions serve as the main
charge carriers in the electrolyte. In these cells, YSZ (yt-
tria-stabilized zirconia) is typically used as the electrolyte
material. If the operating temperature (873-1273 K) were
lowered, the lifespan of the cells would be extended.
Lowering the temperature enables the use of higher
ion-conducting electrolyte materials, such as Sm-doped
ceria electrolytes (SDC).
However, the open current voltage (OCV) using an
SDC cell is about 0.8 V, which is lower than the Nernst
voltage (Vth = 1.15 V) at 1073 K. This low OCV value is
considered to be due to the low value of the ionic trans-
ference number (tion). OCV can be explained by Wag-
ner’s equation [1];
2
2
ln
4
ionion th
pO RT
OCV ttV
FpO
 
 


 (1)
e
ion
ie
R
tRR  (2)
where R, T and F are the gas constant, the absolute tem-
perature in Kelvin and the Faraday constant, 2 pO

and
2
pO

 are the oxygen partial pressures at the cathode and
anode, respectively, and Ri and Re are the ionic resistance
and the electronic resistance of the electrolyte, respec-
tively. In general, tion is not constant in the electrolyte.
Therefore, Wagner’s equation is expressed as [2];
2
22
ln
4
pO
ion
pO
RT
OCVt dpO
F


 (3)
In Equation (3), the experimental verification of leakage
currents is necessary [3,4]. Furthermore, theoretical limi-
tation of Equation (3) was discovered [5]. The constant
voltage loss without leakage currents due to a mixed
ionic and electronic conducting (MIEC) dense anode is
proposed with empirical equation. Furthermore, the mo-
difications of Wagner’s equation are proposed. This topic
is not an isolated and minor topic, but of vital importance
to electrochemical engineering for the 21st Century.
Several future technological applications are also intro-
duced.
2. Experimental
The SDC electrolyte was 25 mm in diameter and 600
mm thick. Porous Pt electrode (10 mm in diameter) was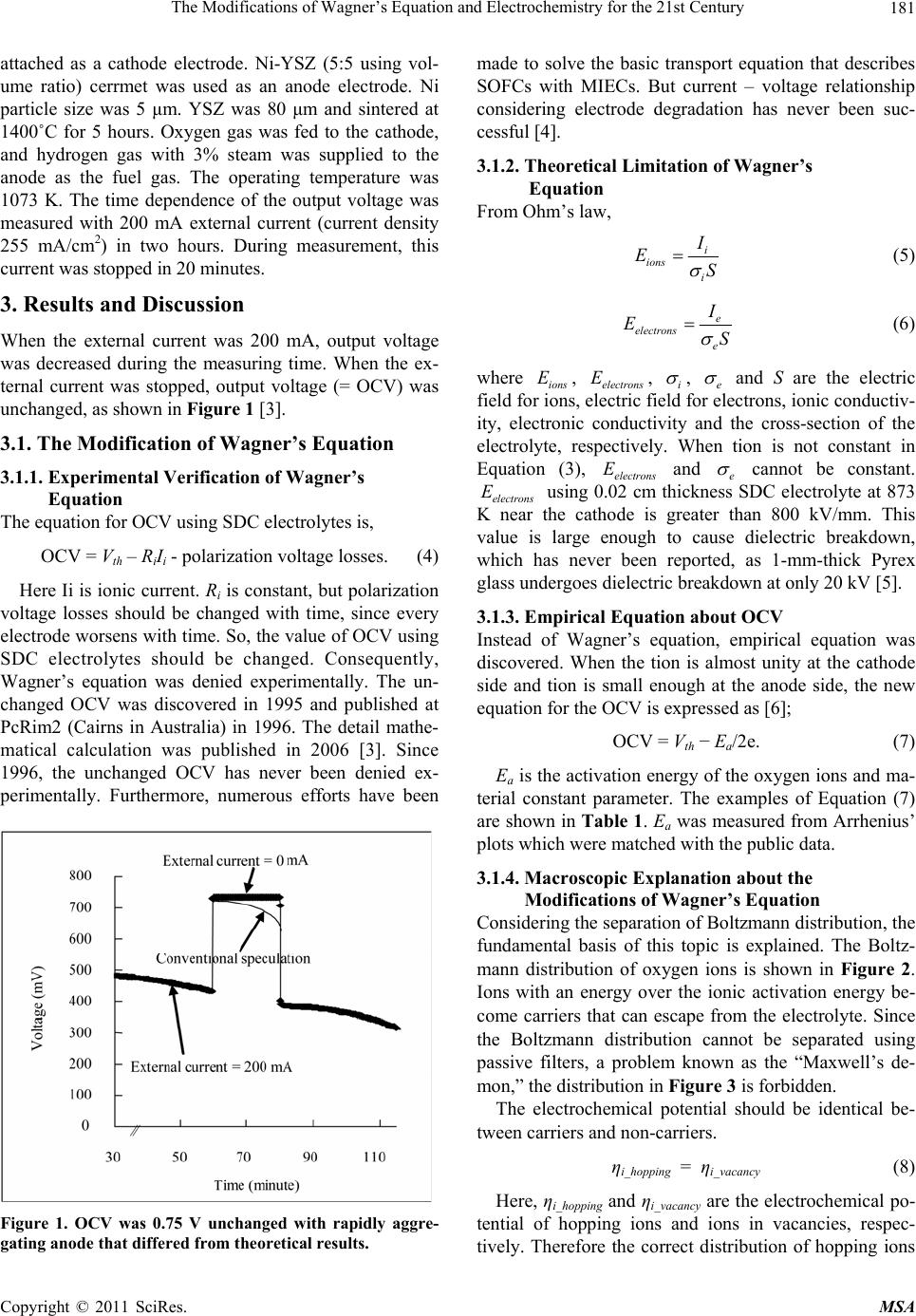

The Modifications of Wagner’s Equation and Electrochemistry for the 21st Century 181
attached as a cathode electrode. Ni-YSZ (5:5 using vol-
ume ratio) cerrmet was used as an anode electrode. Ni
particle size was 5 μm. YSZ was 80 μm and sintered at
1400˚C for 5 hours. Oxygen gas was fed to the cathode,
and hydrogen gas with 3% steam was supplied to the
anode as the fuel gas. The operating temperature was
1073 K. The time dependence of the output voltage was
measured with 200 mA external current (current density
255 mA/cm2) in two hours. During measurement, this
current was stopped in 20 minutes.
3. Results and Discussion
When the external current was 200 mA, output voltage
was decreased during the measuring time. When the ex-
ternal current was stopped, output voltage (= OCV) was
unchanged, as shown in Figure 1 [3].
3.1. The Modification of Wagner’s Equation
3.1.1. Experimental Verification of Wagner’s
Equation
The equation for OCV using SDC electrolytes is,
OCV = Vth – RiIi - polarization voltage losses. (4)
Here Ii is ionic current. Ri is constant, but polarization
voltage losses should be changed with time, since every
electrode worsens with time. So, the value of OCV using
SDC electrolytes should be changed. Consequently,
Wagner’s equation was denied experimentally. The un-
changed OCV was discovered in 1995 and published at
PcRim2 (Cairns in Australia) in 1996. The detail mathe-
matical calculation was published in 2006 [3]. Since
1996, the unchanged OCV has never been denied ex-
perimentally. Furthermore, numerous efforts have been
Figure 1. OCV was 0.75 V unchanged with rapidly aggre-
gating anode that differed from theoretical results.
made to solve the basic transport equation that describes
SOFCs with MIECs. But current – voltage relationship
considering electrode degradation has never been suc-
cessful [4].
3.1.2. Theoretical Limitation of Wagner’s
Equation
From Ohm’s law,
i
ions
i
I
ES

 (5)
e
electrons
e
I
ES

 (6)
where ions
E, electrons E, i

, e

and S are the electric
field for ions, electric field for electrons, ionic conductiv-
ity, electronic conductivity and the cross-section of the
electrolyte, respectively. When tion is not constant in
Equation (3), electrons E and e

cannot be constant.
electrons
E using 0.02 cm thickness SDC electrolyte at 873
K near the cathode is greater than 800 kV/mm. This
value is large enough to cause dielectric breakdown,
which has never been reported, as 1-mm-thick Pyrex
glass undergoes dielectric breakdown at only 20 kV [5].
3.1.3. Empirical Equation about OCV
Instead of Wagner’s equation, empirical equation was
discovered. When the tion is almost unity at the cathode
side and tion is small enough at the anode side, the new
equation for the OCV is expressed as [6];
OCV = Vth − Ea/2e. (7)
Ea is the activation energy of the oxygen ions and ma-
terial constant parameter. The examples of Equation (7)
are shown in Table 1. Ea was measured from Arrhenius’
plots which were matched with the public data.
3.1.4. Macroscopic Explanation about the
Modificati o ns of Wagner’s Equation
Considering the separation of Boltzmann distribution, the
fundamental basis of this topic is explained. The Boltz-
mann distribution of oxygen ions is shown in Figure 2.
Ions with an energy over the ionic activation energy be-
come carriers that can escape from the electrolyte. Since
the Boltzmann distribution cannot be separated using
passive filters, a problem known as the “Maxwell’s de-
mon,” the distribution in Figure 3 is forbidden.
The electrochemical potential should be identical be-
tween carriers and non-carriers.
ηi_hopping = ηi_vacancy (8)
Here, ηi_hopping and ηi_vacancy are the electrochemical po-
tential of hopping ions and ions in vacancies, respec-
tively. Therefore the correct distribution of hopping ions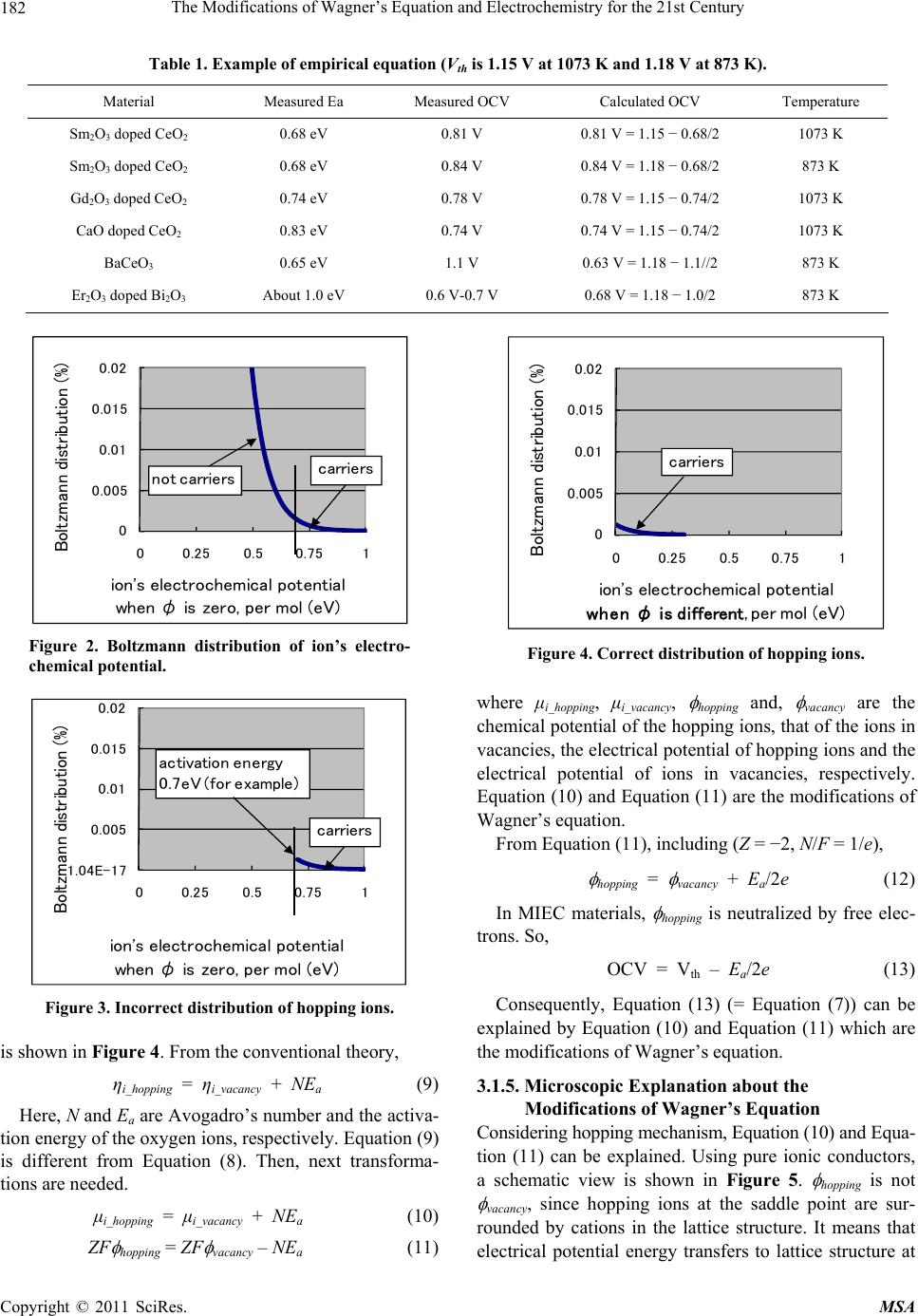

The Modifications of Wagner’s Equation and Electrochemistry for the 21st Century 182
Table 1. Example of empirical equation (Vth is 1.15 V at 1073 K and 1.18 V at 873 K).
Material Measured Ea Measured OCV Calculated OCV Temperature
Sm2O3 doped CeO2 0.68 eV 0.81 V 0.81 V = 1.15 − 0.68/2 1073 K
Sm2O3 doped CeO2 0.68 eV 0.84 V 0.84 V = 1.18 − 0.68/2 873 K
Gd2O3 doped CeO2 0.74 eV 0.78 V 0.78 V = 1.15 − 0.74/2 1073 K
CaO doped CeO2 0.83 eV 0.74 V 0.74 V = 1.15 − 0.74/2 1073 K
BaCeO3 0.65 eV 1.1 V 0.63 V = 1.18 − 1.1//2 873 K
Er2O3 doped Bi2O3 About 1.0 eV 0.6 V-0.7 V 0.68 V = 1.18 − 1.0/2 873 K
0
0.005
0.01
0.015
0.02
00.250.5 0.751
Boltzmann distribution (%)
ion's electrochemical potential
when φ is zero, per mol (eV)
carriers
not carriers
Figure 2. Boltzmann distribution of ion’s electro-
chemical potential.
-1.04E-17
0.005
0.01
0.015
0.02
00.250.5 0.751
Boltzmann distribution (%)
ion's electrochemical potential
when φ is zero, per mol(eV)
carriers
activation energy
0.7eV (for example)
Figure 3. Incorrect distribution of hopping ions.
is shown in Figure 4. From the conventional theory,
ηi_hopping = ηi_vacancy + NEa (9)
Here, N and Ea are Avogadro’s number and the activa-
tion energy of the oxygen ions, respectively. Equation (9)
is different from Equation (8). Then, next transforma-
tions are needed.
μi_hopping = μi_vacancy + NEa (10)
ZF 
hopping = ZF

vacancy – NEa (11)
0
0.005
0.01
0.015
0.02
00.250.5 0.751
Boltzmann distribution (%)
ion's electrochemical potential
when φ is different, per mol(eV)
carriers
Figure 4. Correct distribution of hopping ions.
where μi_hopping, μi_vacancy,

hopping and,

vacancy are the
chemical potential of the hopping ions, that of the ions in
vacancies, the electrical potential of hopping ions and the
electrical potential of ions in vacancies, respectively.
Equation (10) and Equation (11) are the modifications of
Wagner’s equation.
From Equation (11), including (Z = −2, N/F = 1/e),

hopping =

vacancy + Ea/2e (12)
In MIEC materials, 
hopping is neutralized by free elec-
trons. So,
OCV = Vth – Ea/2e (13)
Consequently, Equation (13) (= Equation (7)) can be
explained by Equation (10) and Equation (11) which are
the modifications of Wagner’s equation.
3.1.5. Microsc opi c Expl a na t i on ab out the
Modificati o ns of Wagner’s Equation
Considering hopping mechanism, Equation (10) and Equa-
tion (11) can be explained. Using pure ionic conductors,
a schematic view is shown in Figure 5. 
hopping is not

vacancy, since hopping ions at the saddle point are sur-
rounded by cations in the lattice structure. It means that
electrical potential energy transfers to lattice structure at

The Modifications of Wagner’s Equation and Electrochemistry for the 21st Century 183
the saddle point and send back to ions just after hopping.
Using MIEC materials, free electrons get the potential
energy of ions at the saddle point. So, 
hopping is neutral-
ized by free electrons and the electrical potential energy
cannot be sent back to ions. A schematic view is shown
in Figure 6. The energy loss is Ea and the voltage loss is
Ea/2e. So,
OCV = Vth – Ea/2e (14)
3.1.6. The Modi fi cation Necessity of Nern st Pl ank
Equation for the 21st Century
About the separation of Boltzmann’s distribution using
passive filter, the problem is known as “Maxwell’s de-
mon” which was already solved by Rolf William Lan-
dauer in 1961. This problem was solved by information
theory, but the effects in the electrochemistry have never
been shown. The effects are observed using MIEC. Not
only Wagner’s equation, but also Nernst-Plank equation
should be modified, since Wagner’s equation is based on
the Nernst-Plank equation.
3.2. Electrochemistry for the 21st Century
3.2.1. The Vol ta ge Me asurement Using MIE C
In Figure 7, the voltage between 1 and 5 can become
lower than the theoretical values when the anode part
becomes MIEC. Without MIEC knowledge, it is impos-
sible to clarify the mechanism of the possible voltage
loss. Deviations of the experimental voltage from the
theoretical voltage can only be attributed to the following
explanations:
1) There are leakage currents.
2) The ion concentrations are different from expected
values.
3) There is contamination from unknown ions.
In order to clarify the mechanism of voltage loss, the
following statement must hold:
“The voltage loss is caused by the MIEC dense layer
without any leakage currents.”
3.2.2. Theoretical Efficiency Using MIEC
Ozone is produced in the 1.25 mm gap from many elec-
Lattice atoms
Saddle poin t
Hopping ion
at saddle point
Thermally excited ions

i_hopping
= 
i _vacancy
+ NE
a

i_hopping
=

i_vacancy
ZF

hopping
= ZF 
vacancy
− NE
a
,
Potential energy sends
back to ions
Figure 5. Schematic view of a different constant in the definitions of chemical potential and electrical potential
during hopping.
Thermally excited ions

i_hopping
= 
i_vacancy
+ NE
a
Hopping ion
at saddle point

hopping
is neutralized .
Potential energy transfer to
free electrons in MIEC
Free electrons get
energy from ions
Hopping ion
at saddle point
Potential energy transfers to lattice
structure
ZF 
hopping
= ZF 
vacancy
− NE
a
,
Figure 6. Schematic view of potential energy loss of ions in MIEC.

The Modifications of Wagner’s Equation and Electrochemistry for the 21st Century 184
trical discharges reacting with oxygen gas shown in Fig-
ure 8:
O2 + electron (electrical discharges) → 2 O (15)
O + O2 → O
3 (16)
The technological efficiency is only 7% of the theo-
Damaged area
to be MIEC
Figure 7. Schematic diagram of an ion channel (from free
Wikipedia, http://en.wikipe dia.org/wiki/Ion_channel) 1:
Channel domains (typically four per channel), 2: Outer
vestibule, 3: Selectivity filter, 4: Diameter of selectivity filter,
5: Phosphorylation site, 6: Cell membrane.
Figure 8. The structure of ozone generator.
Figure 9. Sludge concentration measurement using micro-
wave.
Figure 10. OCV is larger than a single SDC.
Figure11. OCV is smaller than Nernst voltage.
Figure 12. Explanation of rectification between two electro-
lytes.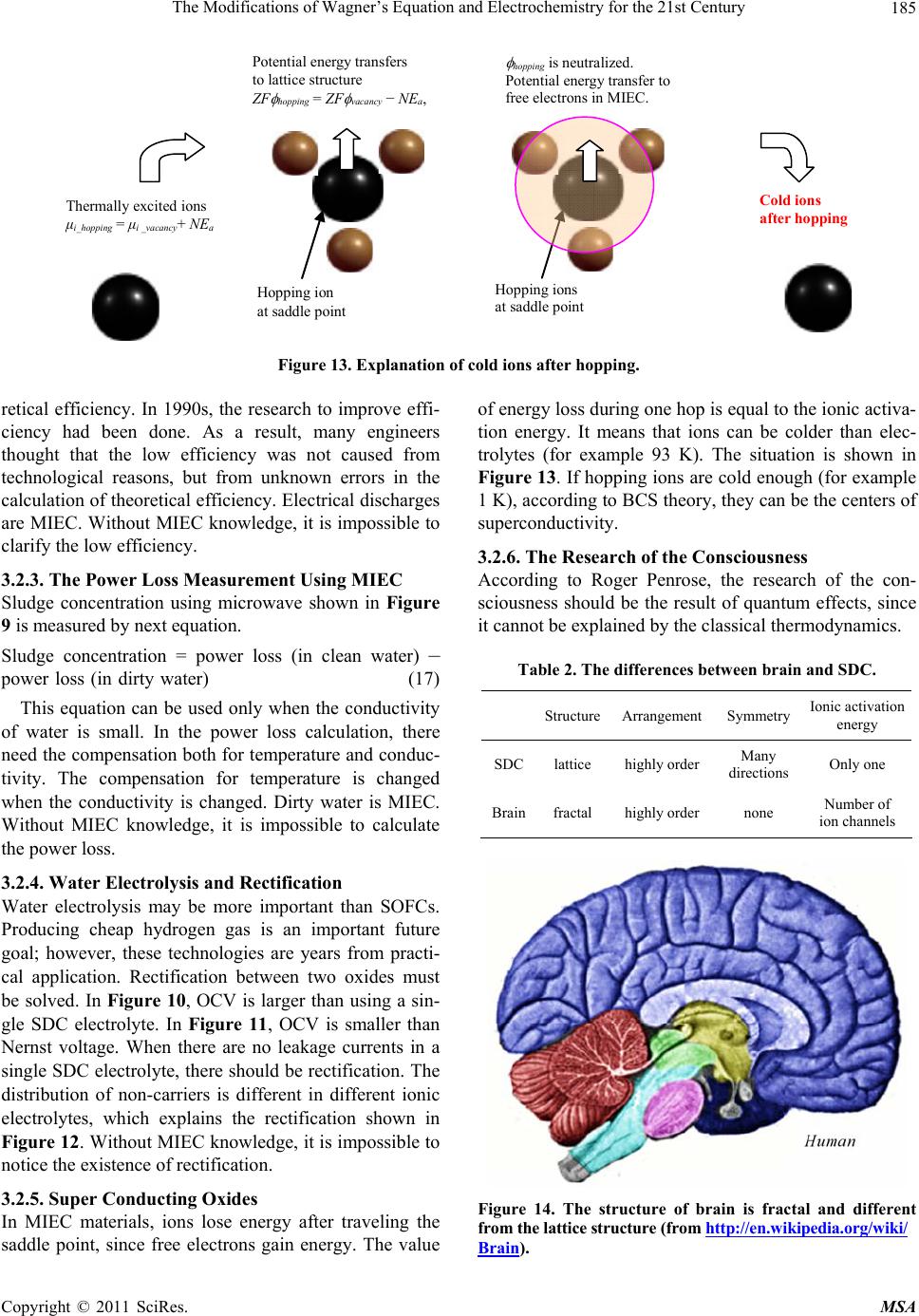

The Modifications of Wagner’s Equation and Electrochemistry for the 21st Century 185
Thermally excited ions
μ
i_hopping
= μ
i _vacancy
+ NE
a
Hopping ions
at saddle point

hopping
is neutralized.
Potential energy transfer to
free electrons in MIEC.
Cold io n s
after hopping
Hopping ion
at saddle point
Potential energy transfers
to lattice structure
ZF 
hopping
= ZF 
vacancy
− NE
a
,
Figure 13. Explanation of cold ions after hopping.
retical efficiency. In 1990s, the research to improve effi-
ciency had been done. As a result, many engineers
thought that the low efficiency was not caused from
technological reasons, but from unknown errors in the
calculation of theoretical efficiency. Electrical discharges
are MIEC. Without MIEC knowledge, it is impossible to
clarify the low efficiency.
3.2.3. The Power Loss Measurement Using MIEC
Sludge concentration using microwave shown in Figure
9 is measured by next equation.
Sludge concentration = power loss (in clean water) –
power loss (in dirty water) (17)
This equation can be used only when the conductivity
of water is small. In the power loss calculation, there
need the compensation both for temperature and conduc-
tivity. The compensation for temperature is changed
when the conductivity is changed. Dirty water is MIEC.
Without MIEC knowledge, it is impossible to calculate
the power loss.
3.2.4. Water Electrolysis and Rectification
Water electrolysis may be more important than SOFCs.
Producing cheap hydrogen gas is an important future
goal; however, these technologies are years from practi-
cal application. Rectification between two oxides must
be solved. In Figure 10, OCV is larger than using a sin-
gle SDC electrolyte. In Figure 11, OCV is smaller than
Nernst voltage. When there are no leakage currents in a
single SDC electrolyte, there should be rectification. The
distribution of non-carriers is different in different ionic
electrolytes, which explains the rectification shown in
Figure 12. Without MIEC knowledge, it is impossible to
notice the existence of rectification.
3.2.5. Super Cond ucting Oxides
In MIEC materials, ions lose energy after traveling the
saddle point, since free electrons gain energy. The value
of energy loss during one hop is equal to the ionic activa-
tion energy. It means that ions can be colder than elec-
trolytes (for example 93 K). The situation is shown in
Figure 13. If hopping ions are cold enough (for example
1 K), according to BCS theory, they can be the centers of
superconductivity.
3.2.6. The Research of the Consciousness
According to Roger Penrose, the research of the con-
sciousness should be the result of quantum effects, since
it cannot be explained by the classical thermodynamics.
Table 2. The differences between brain and SDC.
StructureArrangement Symmetry
Ionic activation
energy
SDClattice highly order Many
directions Only one
Brainfractal highly order none Number of
ion channels
Figure 14. The structure of brain is fractal and different
from the lattice structure (from http://en.wikipe dia. org/wiki/
Brain).

The Modifications of Wagner’s Equation and Electrochemistry for the 21st Century 186
Figure 15. Without MIEC knowledge, it is impossible to
notice the voltage down of neurotransmitter receptors. (From
http://en.wikipedia.org/wiki/Major_depressive_disorder#M
onoamine_hypothesis).
But the classical thermodynamics is not completed still
yet. Many mental diseases are caused from the illness of
ion channels and many medicines are effective for ion
channels. The differences between brain and SDC are
shown in Table 2. The role of ionic activation energy is
something internal dimensions. The fundamental mean-
ing of the internal dimension is discussed [8]. The num-
ber of internal dimensions in theoretical physics is dis-
cussed empirically [9]. Internal dimensions in the brain
are large enough to explain the consciousness, since there
are numerous ion channels in the brain. The research of
the consciousness should be in the area of electrochemis-
try. The fundamental thermo dynamical research of
MIEC is needed.
3.2.7. The Mechanism of Depression
Depressive disorder is explained by monoamine hy-
pothesis since 1980s. Using the present technology, the
hypothesis cannot be confirmed still yet. When the detail
mechanism of hypothesis will be clarified, the numerous
people will be helped. The neurotransmitter receptors
may be voltage down by the reduction of dense anode
area where the parts were damaged to be MIEC.
4. Conclusions
Instead of the leakage current using Sm doped Ceria
electrolytes in SOFCs, the constant voltage loss is pro-
posed. Considering the separation of Boltzmann distribu
tion and Maxwell’s demon, the modifications of Wag-
ner’s equation are proposed. Wagner’s equation is based
on the Nernst-Plank equation. So, when the modifica-
tions are needed in Wagner’s equation, the modifications
of Nernst-Plank equation are needed. It means that the
classical thermodynamics is not finished in the funda-
mental level. The effects of the modification are ob-
served in MIEC. This topic is not an isolated and minor
topic, but of vital importance to the scientific commu-
nity.
5. Acknowledgements
This report is rewritten from the ECS transaction [7].
REFERENCES
[1] C. Wagner, “Beitrag zur Theorie des Anlaufvorgangs,”
Zeitschrift für Physikalische Chemie, Vol. B41, 1933, p.
42.
[2] H. Rickert, “Electrochemistry of Solids—An Introduc-
tion,” Springer, Berlin, Heidelberg, 1982.
[3] T. Miyashita, “Necessity of Verification of Leakage Cur-
rents Using Sm Doped Ceria Electrolytes in SOFCs,”
Journal of Materials Science, Vol. 41, No. 10, 2006, pp.
3183-3184. doi:10.1007/s10853-006-6371-8
[4] T. Miyashita, “Current-Voltage Relationship Considering
Electrode Degradation Using Sm-Doped Ceria Electro-
lytes in SOFCs,” ECS Transactions, Vol. 35, 2011. (In
Press).
[5] T. Miyashita, “The Limitations of Wagner’s Equation in
Solid-State Electrochemistry,” ECS Transactions, Vol. 33,
No. 32, 2011, pp. 11-18. doi:10.1149/1.3562554
[6] T. Miyashita, “Empirical Equation about Open Circuit
Voltage in SOFC,” Journal of Materials Science,Vol. 40,
No. 22, 2005, p. 6027. doi:10.1007/s10853-005-4560-5
[7] T. Miyashita, “Fundamental Thermodynamic Modifica-
tions in Wagner’s Equation in Solid State Electrochemis-
try,” ECS Transactions, Vol. 28, 2010, pp. 39-49.
doi:10.1149/1.3502443
[8] T. Miyashita, “Quantum Physics can be Understood in
Terms of Classical Thermodynamics,” Journal of Modern
Physics, Vol. 2, 2011, pp. 26-29.
doi:10.4236/jmp.2011.31005
[9] T. Miyashita, “Empirical Relations about the Number of
Dimensions in Theoretical Physics with the Concept of
Common and Unshared Dimensions,” Journal of Modern
Physics, Vol. 2, 2010, pp. 147-149.
doi:10.4236/jmp.2010.12021