J. Biomedical Science and Engineering, 2013, 6, 61-70 JBiSE
http://dx.doi.org/10.4236/jbise.2013.612A008 Published Online December 2013 (http://www.scirp.org/journal/jbise/)
Modeling the effects of stretch-dependent surfactant
secretion on lung recruitment during variable ventilation
Samir D. Amin1, Arnab Majumdar1, Phil Alkana2, Allan J. Walkey2, George T. O’Connor2,
Béla Suki1*
1Department of Biomedical Engineering, Boston University, Boston, USA
2School of Medicine, Boston University, Boston, USA
Received 24 October 2013; revised 26 November 2013; accepted 15 December 2013
Copyright © 2013 Samir D. Amin et al. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
Variable ventilation (VV) is a novel strategy of venti-
latory support that utilizes random variations in the
delivered tidal volume (VT) to improve lung function.
Since the stretch pattern during VV has been shown
to increase surfactant release both in animals and cell
culture, we hypothesized that there were combinations
of PEEP and VT during VV that led to improved al-
veolar recruitment compared to conventional me-
chanical ventilation (CV). To test this hypothesis, we
developed a computational model of stretch-induced
surfactant release combined with abnormal alveolar
mechanics of the injured lung under mechanical ven-
tilation. We modeled the lung as a set of distinct acini
with independent surfactant secretion and thus pres-
sure-volume relationships. The rate of surfactant se-
cretion was modulated by the stretch magnitude that
an alveolus experienced per breath. Mechanical ven-
tilation was simulated by delivering a prescribed VT
at each breath. The fractional VT that each acinus
received depended on its local compliance relative to
the total system compliance. Regional variability in
VT thus developed through feedback between stretch
and surfactant release and coupling of regional VT to
ventilator settings. The model allowed us to simulate
patient-ventilator interactions over a wide range of
PEEPs and VTs during CV and VV. Full recruitment
was achieved through VV at a lower PEEP than re-
quired for CV. During VV, the acini were maintained
under non-equilibrium steady-state conditions with
breath-by-breath fluctuations of regional VT. In CV,
alveolar injury was prevented with high-PEEP-low-
VT or low-PEEP-high-VT combinations. In contrast,
one contiguous region of PEEP-VT combinations al-
lowed for full recruitment without overdistention
during VV. We found that maintaining epithelial cell
stretch above a critical threshold with either PEEP or
VT may help stabilize the injured lung. These results
demonstrate the significance of patient-ventilator cou-
pling through the influence of cellular stretch-induced
surfactant release on the whole lung stability.
Keywords: Computational Modeling; Mechanical
Ventilation; Variable Ventilation; Surfactant Secretion
Dynamics
1. INTRODUCTION
Acute lung injury (ALI) and acute respiratory distress
syndrome (ARDS) represent a continuum of lung injury
that affects over 200,000 patients in the US yearly, with a
30% - 40% mortality rate [1]. The ALI and ARDS arise
from either systemic insult (e.g., sepsis, pancreatitis) or
local injury (e.g., pneumonia, aspiration injury) and
manifest as acute inflammatory edema and diffuse alveo-
lar damage. The inflammatory responses result in se-
verely impaired lung function with reduced compliance
and gas exchange, often culminating in respiratory fail-
ure and the need for mechanical ventilation. Currently,
the only therapy that improves survival in ALI/ARDS is
the ARDSNet ventilatory protocol, which decreases ven-
tilator-associated lung injury (VALI) by avoiding alveo-
lar overdistention [2].
In addition to alveolar overdistention injury, VALI can
also be induced through the gradient of normal forces
acting on epithelial cells during the reopening process of
closed units [3,4]. These alveolar collapse-associated
causes of VALI are attenuated by the addition of positive
end expiratory pressure (PEEP), which is intended to
recruit atelectatic lung, prevent alveolar surfactant deple-
tion and end expiratory collapse. Unfortunately, the addi-
*Corresponding author.

S. D. Amin et al. / J. Biomedical Science and Engineering 6 (2013) 61-70 62
tion of PEEP can lead to further overdistention and in-
jury of healthy, high compliance alveolar units [5]. The
success of mechanical ventilation depends on the right
balance between overdistention and cyclic collapse-in-
duced injury [6]. Although the ARDSNet strategy was a
major advance in critical care, this method of mechanical
ventilation did not completely eliminate VALI [7]. Thus,
alternative mechanical ventilation strategies that can bet-
ter balance overdistention and cyclic collapse have been
sought.
Variable ventilation (VV) is a relatively novel strategy
of ventilatory support that utilizes random variations in
the delivered tidal volume (VT) to improve lung function
[Much]. Multiple pre-clinical models of acute lung injury
have shown VV to be superior to conventional mechani-
cal ventilation in inducing endogenous surfactant secre-
tion [8,9], improving alveolar recruitment [10,11], and
reducing cytokine [11,12] and histologic [13] evidence of
VALI. Several mechanisms have been proposed to ex-
plain the benefit from adding variability to mechanical
ventilation including variations along the nonlinear pres-
sure-volume curve of the injured lung [14], time depen-
dent closure and opening [11] and variable stretch-induc-
ed surfactant release [8,9].
Single large stretches have been shown to be a potent
stimulus for surfactant release [15]. On the other hand,
monotonous large amplitude cyclic stretch of epithelial
cells in culture down-regulates surfactant release [8].
Thus, different stretch patterns delivered by a mechanical
ventilation mode should have a significant impact on
surfactant turnover which in turn determines lung com-
pliance and hence patient outcome. To our knowledge,
interactions among PEEP and VT during mechanical ven-
tilation, surfactant release and lung physiology have not
been studied in a systematic way.
Combined with PEEP, VV has been shown to outper-
form CV in recruitment and reduction of epithelial injury
in HCl-injured mice [12]. We thus hypothesized that
there were combinations of PEEP and VT during VV that
led to improved alveolar recruitment through stretch-
induced surfactant release compared to conventional
mechanical ventilation (CV). To test this hypothesis, we
have developed a computational model of stretch-in-
duced surfactant production and release combined with
abnormal alveolar mechanics of the injured lung during
mechanical ventilation. Using this model, we compared
alveolar recruitment-derecruitment behavior over a wide
range of PEEP and VT during both VV and CV.
2. METHODS
We model the lung as a parallel arrangement of NA acinar
units (Figure 1(A)), each with independent surfactant
secretion and thus pressure-volume (P-V) relationship.
Each acinar unit is assumed to consist of many alveoli
which are not modeled separately. Within an acinar unit,
surfactant secreted by type II epithelial cells accumulates
onto the air-liquid interface to reduce surface tension and
thus increase local alveolar compliance (Figure 1(C)).
Epithelial cells secrete surfactant at a rate determined by
the magnitude of stretch their unit experiences over a
given breath (Figure 1(B)). Units that receive either
more or less than average regional VT also experience
correspondingly more or less stretch; over time this will
affect the amount of surfactant accumulated locally at the
air-liquid interface and thus each unit consequently sof-
tens or stiffens.
The model simulates mechanical ventilation by deliv-
ering a prescribed VT to the entire parallel set of acinar
units each breath. The fractional tidal volume (VTi) that
the i-th unit receives depends on its local compliance
relative to the total compliance of the system (Figure
1(D)). Regional variability in VT can thus develop through
1) the feedback between stretch and surfactant release,
and 2) the coupling of regional VT to mechanical venti-
lator settings. We can then compare this coupling behav-
ior during simulated CV and VV of the lung model.
2.1. Modulation of Surfactant Release by
Periodic Stretch
Alveolar tissue stretches to accommodate the variations
in lung volume during ventilation. We define the magni-
tude of stretch ε in a unit over a given breath as the rela-
tive change in surface area at end-expiration AEE to that
at end-inspiration AEI. Thus, ε approximately represents
the biaxial strain the cells experience during tidal venti-
lation assuming that surface area of a single cell is much
smaller than AEE.
It is well documented that surfactant release increases
with stretch amplitude up to moderate strains [15,16],
while large stretch inhibits release [8,16]. It naturally
follows that there must be some intermediate stretch
level that produces a peak in surfactant release, although
the exact relation has yet to be determined.
Thus, to incorporate in the model stretch-induced cel-
lular surfactant release and inhibition (from excessive
stretch) in a simple manner, we assume that the rate of
surfactant release in a unit increases with stretch magni-
tude until ε surpasses a critical threshold ε*, whereby
surfactant release reduces with further stretch magnitude
(Figure 1(B)). A piecewise linear relation is used for
surfactant release rate φ as a function of ε:
*
*
*
*
*
2 2
0 2



*








 





(1)

S. D. Amin et al. / J. Biomedical Science and Engineering 6 (2013) 61-70 63
Note that in the context of the model, the exact linear
shape is not important; it’s the existence of a peak that
we aim to capture. Furthermore this curve only repre-
sents the stretch-dependent fraction of surfactant release,
which is in addition to a baseline rate which we assume
is constant throughout the simulation. This point is
elaborated on in Section 4.2.
2.2. Dynamics of Surfactant Secretion and
Degradation
We propose a simple first order dynamics description of
surfactant secretion (Figure 1(C)). Stretch ε induces the
release of surfactant. At each breath n, a small amount of
surfactant is released from the cells onto the alveolar
air-liquid interface. Interfacial surfactant (S) is simulta-
neously removed through degradation, uptake or other
processes at a rate λ so that S at breath n + 1 is given by:
1(1 ) nn
SS
n


 (2)
2.3. Sigmoidal Pressure-Volume Relation
The volume V of each acinar unit obeys a sigmoid rela-
tion with transpulmonary pressure P:
max
()
1
P
G
V
Ve
 
 (3)
The parameter κ corresponds to the compliance of the
curve, Vmax is the volume at total lung capacity (TLC)
and G is the inflection point. The P-V curve of each
acinus, which we assume is proportional to the entire
volume of the unit, is modulated breath-by-breath by the
available interfacial surfactant Sn as
0
0
n
S
S
n
GGe

 (4)
where S0 is a scaling parameter, and G0 corresponds to
the inflection point of Eq.3 arising solely from the equi-
librium amount of stretch-independent surfactant release.
Thus, an increase in interfacial surfactant shifts the in-
flection point to the left resulting in a higher volume for
a given pressure (Figure 1(D)). This form presented by
[17] was chosen as it captures lung P-V curves under a
variety of conditions, and is further discussed in Section
4.5.2.
2.4. Simulation of Mechanical Ventilation
Ventilation of the model is calculated using a prescribed
PEEP and VT as follows. We assume that all acinar pres-
sures Pi reach equilibrium both at end expiration (EE)
and end inspiration (EI), and thus tissue and surface film
viscoelasticity is immaterial. Thus, at end expiration, the
pressure in each unit is equal to the prescribed PEEP
Figure 1. Total Surfactant Release and Regional Tidal Volume
is Modulated by Periodic Stretch. (A) The lung is divided into
parallel alveolar units each defining an acinus, and ventilated
with a given tidal volume (VT). Individual tidal volumes, and
thus strains, vary with regional compliances. At end-inspiration
with airway pressure PEI each unit can have a different alveolar
surface area AEI. (B) Rate of surfactant secretion φ as a function
of stretch amplitude ε of a single unit. (C) Schematic of the
accumulation of surfactant (S) on the gas-liquid interface. Sur-
factant is also removed from the interface at a rate. (D) Sig-
moid pressure-volume (P-V) relation of a single alveolar unit is
shifted to the left with increasing interfacial surfactant (S). UIP
and LIP denote the upper and lower inflection point, respec-
tively. (E) Strains from previous breaths modulate surfactant
levels which alter the P-V relationship of individual units and
thus the strains for the next breath, resulting in a closed feed-
back loop. See text for further explanation.
with total lung volume VEE. At the end of inspiration, the
total lung volume VEI increases above VEE by the pre-
scribed tidal volume VT which is distributed among the
acinar units labeled with i according to the stiffness of
their individual pressure-volume Pi-Vi curve. Thus,


EE PEEP i
i
VVP

(5a)
TARGETEE T
VVV

 (5b)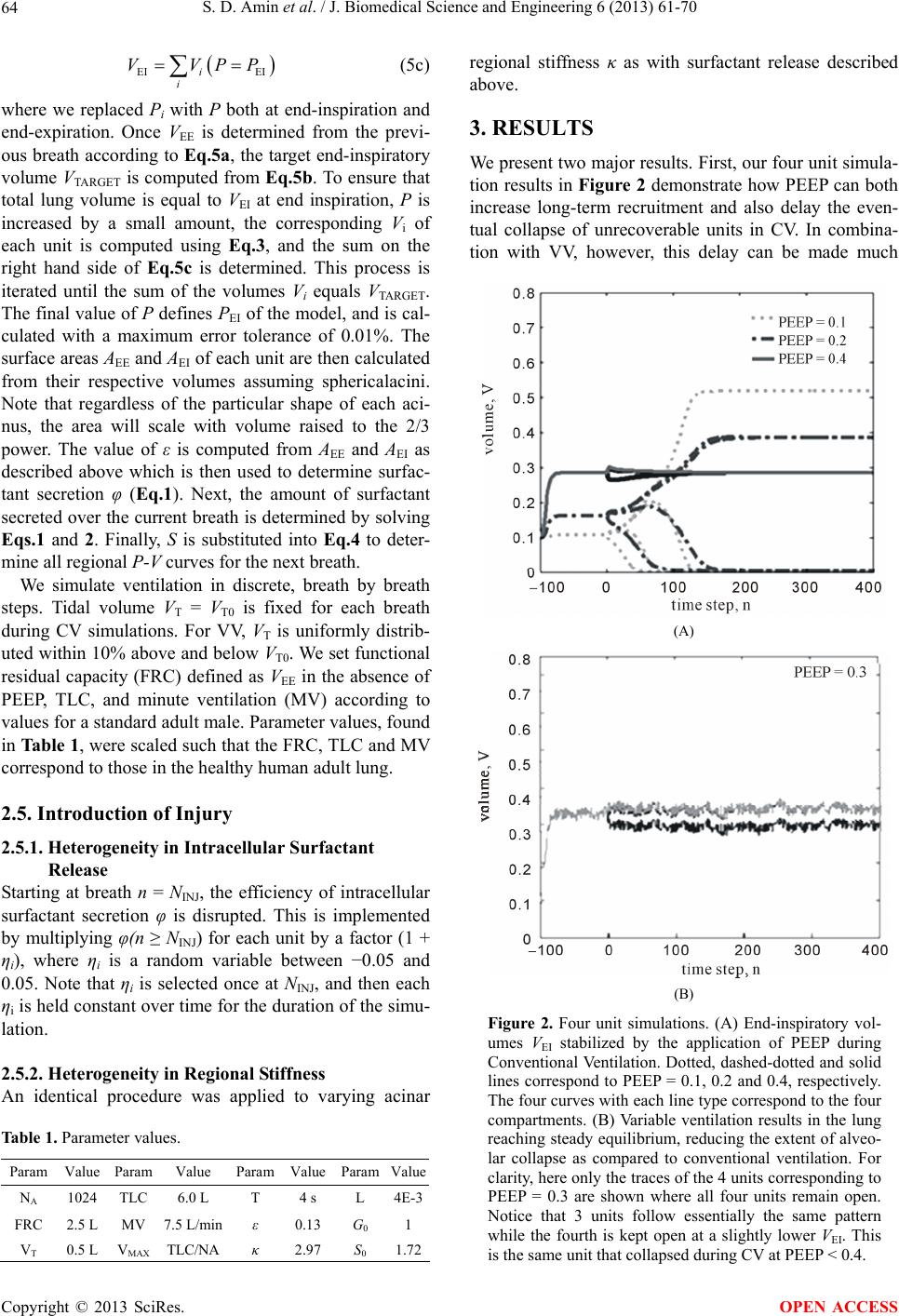

S. D. Amin et al. / J. Biomedical Science and Engineering 6 (2013) 61-70 64

EI EIi
i
VVPP


(5c)
where we replaced Pi with P both at end-inspiration and
end-expiration. Once VEE is determined from the previ-
ous breath according to Eq.5a, the target end-inspiratory
volume VTARGET is computed from Eq.5b. To ensure that
total lung volume is equal to VEI at end inspiration, P is
increased by a small amount, the corresponding Vi of
each unit is computed using Eq.3, and the sum on the
right hand side of Eq.5c is determined. This process is
iterated until the sum of the volumes Vi equals VTARGET.
The final value of P defines PEI of the model, and is cal-
culated with a maximum error tolerance of 0.01%. The
surface areas AEE and AEI of each unit are then calculated
from their respective volumes assuming sphericalacini.
Note that regardless of the particular shape of each aci-
nus, the area will scale with volume raised to the 2/3
power. The value of ε is computed from AEE and AEI as
described above which is then used to determine surfac-
tant secretion φ ( Eq.1). Next, the amount of surfactant
secreted over the current breath is determined by solving
Eqs.1 and 2. Finally, S is substituted into Eq.4 to deter-
mine all regional P-V curves for the next breath.
We simulate ventilation in discrete, breath by breath
steps. Tidal volume VT = VT0 is fixed for each breath
during CV simulations. For VV, VT is uniformly distrib-
uted within 10% above and below VT0. We set functional
residual capacity (FRC) defined as VEE in the absence of
PEEP, TLC, and minute ventilation (MV) according to
values for a standard adult male. Parameter values, found
in Tab le 1, were scaled such that the FRC, TLC and MV
correspond to those in the healthy human adult lung.
2.5. Introduction of Injury
2.5.1. Heterogeneity in Intracellular Surfactant
Release
Starting at breath n = NINJ, the efficiency of intracellular
surfactant secretion φ is disrupted. This is implemented
by multiplying φ(n ≥ NINJ) for each unit by a factor (1 +
ηi), where ηi is a random variable between −0.05 and
0.05. Note that ηi is selected once at NINJ, and then each
ηi is held constant over time for the duration of the simu-
lation.
2.5.2. Hete rogeneity in Re gional Stif fness
An identical procedure was applied to varying acinar
Table 1. Parameter values.
Param Value Param Value Param Value ParamValue
NA 1024 TLC 6.0 L T 4 s L 4E-3
FRC 2.5 L MV 7.5 L/minε 0.13 G0 1
VT 0.5 L VMAX TLC/NA κ 2.97 S0 1.72
regional stiffness κ as with surfactant release described
above.
3. RESULTS
We present two major results. First, our four unit simula-
tion results in Figure 2 demonstrate how PEEP can both
increase long-term recruitment and also delay the even-
tual collapse of unrecoverable units in CV. In combina-
tion with VV, however, this delay can be made much
(A)
(B)
Figure 2. Four unit simulations. (A) End-inspiratory vol-
umes VEI stabilized by the application of PEEP during
Conventional Ventilation. Dotted, dashed-dotted and solid
lines correspond to PEEP = 0.1, 0.2 and 0.4, respectively.
The four curves with each line type correspond to the four
compartments. (B) Variable ventilation results in the lung
reaching steady equilibrium, reducing the extent of alveo-
lar collapse as compared to conventional ventilation. For
clarity, here only the traces of the 4 units corresponding to
PEEP = 0.3 are shown where all four units remain open.
Notice that 3 units follow essentially the same pattern
while the fourth is kept open at a slightly lower VEI. This
is the same unit that collapsed during CV at PEEP < 0.4.

S. D. Amin et al. / J. Biomedical Science and Engineering 6 (2013) 61-70 65
longer as injured units appear to remain at non-equilib-
rium, fluctuating volumes. Second, during ventilation in
the presence of heterogeneous surfactant release or tissue
stiffness, we find that VV can maintain higher recruit-
ment while avoiding overdistention for a wider range of
PEEP and mean VT values, partly through the mechanism
described above.
3.1. Four Unit Simulations
We first simulated CV or VV of a lung model including
only four units, tracing individual VEI over time in Fig-
ure 2 for PEEP values ranging from 0 to 0.4 (in arbitrary
units). The simulations include an initial transient region
between n = −100 and 0, where either CV or VV was
applied in the absence of any injury. At n = 0, heteroge-
neity in intracellular surfactant release was introduced as
described in the Methods, while CV or VV was contin-
ued for another 400 breaths. The injury was identical in
the two cases.
For CV at PEEP = 0.1, three units collapsed following
injury. Increasing PEEP to 0.2, there was a reduction to
only 2 collapsed units and also an increased transient
time for the second compartment to collapse. A full re-
cruitment of all 4 units was still not achieved at PEEP =
0.3, and was qualitatively similar to the PEEP = 0.2 con-
dition (not shown). With PEEP = 0.4, all 4 units are
stretched beyond ε*, and thus we observe stable behavior
with full recruitment. In contrast to CV, full recruitment
was achieved through the use of VV at the lower PEEP
of 0.3. Notice that during VV, the acinar compartments
were maintained under non-equilibrium steady-state con-
ditions with breath-by-breath fluctuations of VEI. Thus,
the variability in delivered tidal volumes prevented the
quick collapse of all injured acini.
3.2. Optimization of PEEP and VT for Maximal
Recruitment with Minimal Overdistention
We next simulated mechanical ventilation with a 1024
unit model as described in the Methods. Again, we
tracked VEI of each individual unit after introduction of
injury at breath n = 0. However, we analyze two types of
injury—heterogeneity in surfactant release and in acinar
stiffness, for 20 values of PEEP and 30 values of VT util-
izing CV and VV. At the end of the simulation, the frac-
tion of collapsed and overdistended units were deter-
mined and plotted as a function of PEEP and VT.
Figure 3 presents the results for CV with heterogene-
ous injury to surfactant release. On the left panel, we see
alveolar collapse with PEEP < 0.5 and VT < 0.5. The ex-
tent of collapse gradually decreases with increasing VT.
On the other hand, there appears to be a distinct thresh-
old around PEEP = 0.4 where collapse is completely
avoided regardless of VT. Overdistention defined as
75%
50%
25%
0.7
0.5
0.3
0.1
V
T0
0.2 0.4 0.6 0.80.2 0.4 0.6 0.8
PEEP
COLLAPSED OVERDISTENDED
Figure 3. Alveolar collapse and overdistention in the presence
of surfactant heterogeneity during conventional ventilation.
Contour plots describe the fraction of the lung in the specified
category when ventilating with a given PEEP and VT. Left:
Fraction of collapsed alveoli reduces gradually with increasing
VT and sharply with PEEP. Right: Fraction of overdistended
alveoli increases with PEEP at high tidal volumes.
VEI = VEE + VT reaching 75% of maximum alveolar vol-
ume showed an opposing trend, where the highest VT
which avoids overdistention decreases approximately
linearly with increasing PEEP. Simultaneous collapse
and overdistention can be observed at midrange values of
PEEP and VT.
Additional simulations allowed us to compare and
contrast the results for applying VV or CV for heteroge-
neous surfactant release as well as heterogeneous acinar
stiffness (Figure 4). For a disruption of normal homoge-
neous surfactant release under CV (top left panel), al-
veolar collapse occurs at low-PEEP-low-VT settings,
while overdistention occurs for high-PEEP-high-VT set-
tings resulting in two relatively small disjoint regions
(blue) whereby alveolar injury is prevented. When VV is
applied (top right panel), one contiguous region of PEEP
and VT allows for full recruitment without overdistention.
Overall, the possible combinations of PEEP and VT dur-
ing VV are much greater than during CV. For the het-
erogeneous acinar stiffness case under CV (bottom left
panel), again alveolar collapse occurs at low-PEEP-low-
VT settings, while overdistention occurs for high-PEEP-
high-VT settings. However, in this case a contiguous band
of good PEEP-VT settings exist. When VV is applied
(right panel), the size of this region is significantly larger.
4. DISCUSSION
In this study, we developed a model that incorporates
stretch-induced surfactant release into the regional pres-
sure-volume curve of a parallel set of acinar units ex-
posed to various ventilator settings. To our knowledge,
this is the first attempt to couple surfactant metabolism
with stretch and regional lung mechanics. The model
allows us to simulate patient-ventilator interactions over
a wide range of PEEPs and VTs. The primary finding of
the study is that the particular ventilator settings have
a critical role in surfactant distribution, regional lung
compliance and hence predicted ventilation outcome.

S. D. Amin et al. / J. Biomedical Science and Engineering 6 (2013) 61-70 66
CV VV
PEEP PEEP
ALTERED
STIFFNESS
V
T0
DISRUPTED
SURFACTANT
V
T0
Figure 4. Comparison of best PEEP-VT settings for CV vs. VV
for two different pathologies. Contour plots describe the frac-
tion of the lung which are neither collapsed nor overdistended
when ventilating with a given PEEP and VT for CV and VV. For
instance, the top left panel shows the superimposed view of
Figures 3(A) and (B), presenting the PEEP and VT settings
which resulted in the best outcomes (number of units recruited
but not overdistended) in blue and injury due to collapse or
overdistention marked by red. Top left: Heterogeneous surfac-
tant release under CV. Top right: Heterogeneous surfactant
release under VV. Bottom left: Heterogeneous alveolar stiffness
under CV. Bottom right: Heterogeneous alveolar stiffness under
VV.
Specifically, VV provides a much wider range of possi-
ble ventilator settings that result in maximum lung re-
cruitment and minimal overdistention when compared to
CV.
4.1. Optimal PEEP-VT Values for CV and VV
In this model, alveolar collapse is prevented by stretch-
ing the acinar units above ε*. This can be accomplished
through either large tidal stretches alone, by providing a
sufficiently high PEEP such that ε > ε* at end expiration,
or by a combination of both ventilator settings. This is
reflected in the lower left-hand corner of each panel in
Figure 4: low PEEP and small VT leads to collapse
whereas large VT values provide adequate stretch and
surfactant release. With increasing PEEP, a lower VT is
sufficient to produce the necessary stretch. At around
PEEP = 0.4, the end-expiratory pressure alone is suffi-
cient to maintain alveolar recruitment. Naturally, there is
an inverse relationship between the VT and PEEP re-
quired to reach the absolute volume beyond which over-
distention of the alveoli occurs. The reason for this is that
PEEP effectively increases VEE. These characteristics are
common to each simulation case.
The difference between VV and CV are illustrated in
the presence of heterogeneous surfactant release in the
top panels of Figure 4. As some acinar units collapse,
their volume is diverted into the remaining units trigger-
ing simultaneous collapse and overdistention as seen in
the top left panel of Figure 4. However, we observe that
VV allows for full recruitment at a lower VT than CV. In
fact, the overlapping region of collapse and overdisten-
tion is completely removed. Overall, a larger range of
PEEP and VT can provide optimal acinar recruitment
(area of the blue regions) in VV than for CV.
We also note here a qualitative difference between the
results for the two injury cases during CV. In the pres-
ence of heterogeneous stiffness, we no longer observe an
area of simultaneous collapse and overdistention. The
model also predicts a larger area of overdistention, and
low-PEEP-high-VT settings no longer produce a positive
outcome (defined as full recruitment). In contrast, the
acceptable combinations of PEEP and VT during VV
seem to be insensitive to the simulated injuries. Addi-
tional sensitivity analysis, in which model parameters
were varied between 50% and 200% of their baseline
values, indicated that the advantage of VV over CV is
robust and does not depend on particular model settings.
In both cases of injury during VV, there exists an un-
expected region at intermediate PEEPs where increasing
tidal volume first causes and then prevents overdistention.
We note that these PEEP-VT combinations are well above
physiologic values, and discuss this further in the section
on model limitations.
4.2. Stability of the Alveolus through
Stretch-Surfactant Relation
The shape of the stretch-surfactant relationship (Figure
1(B)), in particular its peak, has two consequences on
model behavior. First, there appears to be an optimal
stretch magnitude for surfactant secretion, and thus re-
duction of mechanical injury induced by ventilation. The
second, seemingly counterintuitive, consequence is that
optimal lung function actually requires the majority of
the lung to be stretched beyond this threshold. Consider
an alveolus ventilated at or below the stretch threshold ε*.
A minor reduction in stretch attenuates surfactant pro-
duction, increasing stiffness which in turn further reduces
stretch, eventually leading to full collapse. This is in
agreement with recent data that ventilating normal mice
at a PEEP of 3 cm H2O for 30 min, a reduction in VT
from 8 to 6 ml/kg significantly reduced the level of sur-
factant protein B, a key component of surfactant that
contributes to normal surface tension [18]. In contrast, in
the regime above the stretch threshold, reduced/increased
alveolar stretch increases/reduces surfactant production,
and thus deviations from the initial stretch magnitude are
countered by the stretch modulated surfactant secretion.

S. D. Amin et al. / J. Biomedical Science and Engineering 6 (2013) 61-70 67
In other words, an inverse relation between stretch and
surfactant secretion beyond the critical value ε*, in com-
bination with the nonlinear pressure-volume relationship,
guarantees the stability of acinar units.
4.3. Coupling of Local Surfactant Secretion and
Compliance to Regional Ventilation
Next, we consider several connected acinar units venti-
lated at a fixed global tidal volume such that the alveolar
stretch magnitudes are beyond ε*. If one alveolus is in-
jured and thus stretched below the threshold, it would
tend to collapse according to the mechanism described in
Section 4.2, diverting its tidal volume into the remaining
normal alveoli. This extra volume causes the normal al-
veoli to be stretched further above the threshold, reduc-
ing their surfactant thus increasing their stiffness. This
redirects flow back into the injured unit, increasing its
surfactant production possibly preventing collapse. This
protective mechanism no longer holds, however, when
the entirety of units are also stretched below the thresh-
old. After a large fraction of the units collapse, the di-
verted tidal volume is forced into the small remaining
open fraction of the units resulting in their overdistention.
Consequently, a heterogeneous distribution of severe
injury through surfactant interference or local trauma can
result in neighboring regions of collapsed and overdis-
tended acinar units. Images of subpleural alveoli of nor-
mal and ventilator-injured lungs are consistent with this
notion (10). Thus, maintaining above-threshold stretch
with either PEEP or tidal volume may help stabilize the
injured lung.
4.4. Non-Equilibrium Steady State during
Variable Ventilation
Through the proposed mechanisms, progressive alveolar
collapse and ventilation redistribution occurred due to
the instability of the system when stretch is below ε*.
During CV, the final outcome (e.g. whether an acinus
collapses) was a function of the stretch magnitude of
each acinus relative to the threshold. The time scale of
collapse depended primarily on surfactant dynamics (φ
and λ) and tidal volume, and in many cases a long tran-
sient period preceded equilibrium. During VV, the cy-
cle-by-cycle variations of regional tidal volumes dis-
rupted the stretch-surfactant coupling, prolonging this
transient period indefinitely. Indeed, such dynamic equi-
librium has been found experimentally in mice during
ventilation with VV [19]. In our model, this steady state
maintains on average a larger number of recruited acinar
units than CV. We can speculate that in real patients, if
such steady state exists, it may allow time for the injury
to heal and thus faster return to normal function upon
release from the ventilator. We also note that experimen-
tally it was found that VV stimulates surfactant release as
well as production [20]. Our simulations are consistent
with this since on average a higher lung volume in the
model is due to more surfactant. Thus, the non-equilib-
rium steady state seen in the model offers a mechanistic
explanation for such experimental findings.
4.5. Model Limitations
Several assumptions in our model were implemented to
simplify the dynamics and study regional surfactant me-
tabolism coupled with regional alveolar stretch. Addi-
tionally, several important phenomena have also been
neglected. These are discussed next.
4.5.1. Modeling Stretch-Induced Surfactant Release
Little is known about the stretch-induced dynamics of
surfactant release and production in vivo. In vitro studies
suggest that increasing the amplitude of a single biaxial
stretch applied to cells in culture, increases the amount of
surfactant released in a quasi-exponentially increasing
manner while the time course of the release showed an
asymptotic approach to a constant [15]. During cyclic
stretch; however, large amplitudes down-regulated sur-
factant release [8]. The shape of the surfactant release-
stretch curve in our model (Figure 1(B)) incorporated
these observations. As described in Section 4.2, it is the
slope of the stretch-surfactant curve below and above the
peak that drives the stability of the overall system. In
light of this, our choice of a linear relation as opposed to
another would not qualitatively affect our results. This
feature of the model together with how surfactant affects
the pressure-volume curve (Figure 1(D)) led to the pre-
diction of reversal of overdistention with unphysiologi-
cally large VT values superimposed on medium PEEP
levels. Nevertheless, VV still outperformed CV even if
we did not include this region in the comparison.
4.5.2. Pressure - Vo l u me Relation
We selected the empirical pressure-volume relation pre-
sented by [17] as it is able to capture the convex P-V
relation at low volumes resulting from recruitment and
the plateau at high pressures due to tissue stiffening. Our
implicit assumption is that the P-V relation on the scale
of individual acinar units is similar to that of the whole
lung. In this manner, we are able to parameterize indi-
vidual acinar units based on published values corre-
sponding to whole lung data [17]. The disadvantage of an
empirical curve is that it does not account for the contri-
bution of tissue and surface forces separately.
Although the relation presented by Bachofen and
Wilson [21] and subsequent modifications [22,23] ex-
plicitly includes the micromechanical response of fiber
stretch and surface tension within individual acini, it is
unsuitable to our needs as its applicability is limited be-

S. D. Amin et al. / J. Biomedical Science and Engineering 6 (2013) 61-70 68
tween 40% and 80% of TLC, whereas our model neces-
sarily contains acini outside of this range. The model
presented by Denny and Shroter [24] contain surface and
tissue forces similar to that of [21] at the level of indi-
vidual acini, showing a sigmoidal relation qualitatively
similar to [17] for the full range of volumes, but lacks an
analytic P-V relation. We note that similar to the stretch-
surfactant relation, the exact P-V relation does not quail-
tatively affect our results, but rather the second deriva-
tive of this curve (how stiffness varies with volume). Any
sufficiently similar P-V curve would deliver similar re-
sults.
4.5.3. P a rameter Selection
The exact values of many of our model parameters are
difficult to quantify in vivo, and thus remain unknown.
For instance, φmax corresponds to the peak surfactant re-
lease rate per cell at a given stretch amplitude and fre-
quency, while λ is the collective rate of several processes
of surfactant depletion (re-uptake, enzymatic reuptake,
de-activation, etc.). The exact shape of the φ versus ε
relation is also unknown, and the effect of surfactant on
the static P-V relationship of a single alveolus was only
estimated as shifting the curve along the pressure-axis.
To justify our parameter selection, we note that changing
φmax in our model amounts to multiplying φ by a constant
proportionality factor for all units, and would not change
the overall system’s qualitative behavior. The degrada-
tion parameter λ effectively “smoothens out” the changes
in surfactant from each breath: λ = 1 corresponds to im-
mediate degradation of surfactant after each breath. Thus,
adjusting λ affects the time course of collapse which is
not systematically analyzed in this study, and does not
alter the end result of the number of stable and collapsed
acini. For the normal uninjured lung, we chose the values
of φmax, λ, G0, and ε* to correspond to a lung with FRC =
2.5 L and TLC = 6 L while ventilated with VT = 0.5 L
and PEEP = 0.
4.5.4. Breath-by-Breath Dynamics
Assuming full equilibrium of pressures both at end-ex-
piration and end-inspiration neglected the presence in-
tra-breath dynamics and discounted the effects of tissue
and surface film viscoelasticity. As a result, the model is
unable to reproduce hyperinflation, and the time de-
pendence of the opening and closing processes has been
neglected [25] that would likely further complicate the
process of gradual collapse in the model. The surface
area-surface tension loop depends on the constituents of
the surfactant at the air-liquid interface and exhibits hys-
teresis during a breath cycle in overinflated but otherwise
normal regions [26] which is not taken into account.
4.5.5. Parallel Compartment Model
Another simplification was that we modeled a parallel
set of units; hence, any effects due to airway structure are
absent. One important aspect of this may be that repeated
airway opening and closing can produce shear and/or
normal stresses [27] that would amplify epithelial injury.
A further limitation is that due to the previous assump-
tion of pressure equilibrium, applying a different path-
way resistance for each parallel compartment would not
introduce heterogeneous regional flow delivery and pres-
sure fluctuations [28]. Additionally, inter-regional air-
flows causing heterogeneous emptying of the lung are
not possible in our model.
4.5.6. Independent Lung Regions
In the current model, the coupling between regions is
attributed to the redirection of tidal volume from stiffer
to softer compartments in the presence of a fixed total
tidal volume. The effects of fluid accumulation and the
corresponding effects of gravity were not taken into ac-
count. Both of these phenomena have been shown to
play a role in VALI (8) and future extensions of the
model should explicitly incorporate them. Additionally,
mechanical coupling through parenchymal interactions
likely promotes regional interdependence.
4.5.7. Limited Injury Mechanisms
Finally, our models of lung injury at the alveolar and
cellular levels are non-specific. For example, fluid leak-
age from the vasculature alters the composition and
hence the surface-tension surface area relation of the sur-
factant [26]. Fluid accumulation in the alveoli changes
the shape of the local P-V curve with a significant de-
crease in compliance [29]. These mechanisms of lung
injuries should be explored since it is possible that the
best PEEP-VT combination is injury specific. For in-
stance, atelectatic opening and closing may cause more
lung injury than sustained collapse, as could high strain
magnitudes without overdistention leading cell mem-
brane rupture [30].
Despite the limitations discussed above, the novel
features of the model allowed us to explore patient-ven-
tilator coupling and optimization of best PEEP-VT com-
bination in the presence of collapse and overdistention
injury. The main result was that the coupling between
surfactant secretion and regional lung mechanics during
ventilation has a significant impact on the outcome of
patient ventilation. While this was possible only using an
appropriate computational model due to the difficulties
associated with the breath-by-breath experimental as-
sessment of surfactant pool and regional lung mechanics,
the long-term predictions of the model could be tested in
clinical settings.
5. CONCLUSION
It is now well-acknowledged that protecting epithelial

S. D. Amin et al. / J. Biomedical Science and Engineering 6 (2013) 61-70 69
cells from injury is the most important goal of any venti-
lation strategy. The model developed in this study dem-
onstrates the significance of the cellular stretch-induced
surfactant release relationship with respect to the whole
lung stability. Maintaining epithelial cell stretch above a
critical threshold with either PEEP or VT may help stabi-
lize the injured lung. Moreover, the injured lung can see
additional benefit from breath-by-breath variation of tid-
al volumes which maintains the lung periphery open un-
der a dynamic equilibrium with a better outcome than the
corresponding conventional ventilation strategy. Thus,
irrespective of the particular model used in this study,
our results point to the clinical significance of ventila-
tor-patient coupling.
6. ACKNOWLEDGEMENTS
Funded by HL-098976, HL-111745, DoD W81XWH-08-1-0148 and
the Coulter Foundation.
REFERENCES
[1] Rubenfeld, G.D., Caldwell, E., Peabody, E., Weaver, J.,
Martin, D.P., Neff, M., Stern, E.J. and Hudson, L.D.
(2005) Incidence and outcomes of acute lung injury. The
New England Journal of Medicine, 353, 1685-1693.
http://dx.doi.org/10.1056/NEJMoa050333
[2] The Acute Respiratory Distress Syndrome Network
(2000) Ventilation with lower tidal volumes as compared
with traditional tidal volumes for acute lung injury and
the acute respiratory distress syndrome. The New Eng-
land Journal of Medicine, 342, 1301-1308.
http://dx.doi.org/10.1056/NEJM200005043421801
[3] Bilek, A.M., Dee, K.C. and Gaver 3rd., D.P. (2003) Me-
chanisms of surface-tension-induced epithelial cell dam-
age in a model of pulmonary airway reopening. Journal
of Applied Physiology, 94, 770-783.
[4] Kay, S.S., Bilek, A.M., Dee, K.C. and Gaver 3rd., D.P.
(2004) Pressure gradient, not exposure duration, deter-
mines the extent of epithelial cell damage in a model of
pulmonary airway reopening. Journal of Applied Physi-
ology, 97, 269-276.
http://dx.doi.org/10.1152/japplphysiol.01288.2003
[5] Puybasset, L., Gusman, P., Muller, J.C., Cluzel, P., Coriat,
P. and Rouby, J.J. (2000) Regional distribution of gas and
tissue in acute respiratory distress syndrome. III. Conse-
quences for the effects of positive end-expiratory pressure.
CT Scan ARDS Study Group. Adult Respiratory Distress
Syndrome. Intensive Care Medicine, 26, 1215-1227.
http://dx.doi.org/10.1007/s001340051340
[6] Rouby, J.J. and Brochard, L. (2007) Tidal recruitment
and overinflation in acute respiratory distress syndrome:
Yin and yang. American Journal of Respiratory and Cri-
tical Care Medicine, 175, 104-106.
http://dx.doi.org/10.1164/rccm.200610-1564ED
[7] Terragni, P.P., Rosboch, G., Tealdi, A., Corno, E.,
Menaldo E, Davini, O., Gandini, G., Herrmann, P., Mas-
cia, L., Quintel, M., Slutsky, A.S., Gattinoni, L. and Rani-
eri, V.M. (2007) Tidal hyperinflation during low tidal
volume ventilation in acute respiratory distress syndrome.
American Journal of Respiratory and Critical Care Me-
dicine, 175, 160-166.
http://dx.doi.org/10.1164/rccm.200607-915OC
[8] Arold, S.P., Bartolak-Suki, E. and Suki, B. (2009) Vari-
able stretch pattern enhances surfactant secretion in alve-
olar type II cells in culture. American Journal of Physi-
ology: Lung Cellular and Molecular Physiology, 296,
L574-L581.
http://dx.doi.org/10.1152/ajplung.90454.2008
[9] Arold, S.P., Suki, B., Alencar, A.M., Lutchen, K.R. and
Ingenito, E.P. (2003) Variable ventilation induces endo-
genous surfactant release in normal guinea pigs. Ameri-
can Journal of Physiology: Lung Cellular and Molecular
Physiology, 285, L370-L375.
[10] Arold, S.P., Mora, R., Lutchen, K.R., Ingenito, E.P. and
Suki, B. (2002) Variable tidal volume ventilation im-
proves lung mechanics and gas exchange in a rodent
model of acute lung injury. American Journal of Respi-
ratory and Critical Care Medicine, 165, 366-371.
http://dx.doi.org/10.1164/ajrccm.165.3.2010155
[11] Bellardine, C.L., Hoffman, A.M., Tsai, L., Ingenito, E.P.,
Arold, S.P., Lutchen, K.R. and Suki, B. (2006) Compari-
son of variable and conventional ventilation in a sheep
saline lavage lung injury model. Critical Care Medicine,
34, 439-445.
http://dx.doi.org/10.1097/01.CCM.0000196208.01682.87
[12] Thammanomai, A., Hueser, L.E., Majumdar, A., Barto-
lak-Suki, E. and Suki, B. (2008) Design of a new variable-
ventilation method optimized for lung recruitment in
mice. Journal of Applied Physiology, 104, 1329-1340.
http://dx.doi.org/10.1152/japplphysiol.01002.2007
[13] Spieth, P.M., Carvalho, A.R., Pelosi, P., Hoehn, C.,
Meissner C., Kasper, M., Hubler, M., von Neindorff, M.,
Dassow, C., Barrenschee, M., Uhlig, S., Koch, T. and de
Abreu, M.G. (2009) Variable tidal volumes improve lung
protective ventilation strategies in experimental lung in-
jury. American Journal of Respiratory and Critical Care
Medicine, 179, 684-693.
http://dx.doi.org/10.1164/rccm.200806-975OC
[14] Suki, B., Alencar, A.M., Sujeer, M.K., Lutchen, K.R.,
Collins, J.J., Andrade Jr., J.S., Ingenito, E.P., Zapperi, S.
and Stanley, H.E. (1998) Life-support system benefits
from noise. Nature, 393, 127-128.
http://dx.doi.org/10.1038/30127
[15] Wirtz, H.R. and Dobbs, L.G. (1990) Calcium mobiliza-
tion and exocytosis after one mechanical stretch of lung
epithelial cells. Science, 250, 1266-1269.
http://dx.doi.org/10.1126/science.2173861
[16] Arold, S.P. (2006) Effects of cyclic stretch on surfactant
secretion and cell viability in alveolar epithelial cells
grown in culture Diss. ProQuest, Boston University, UMI
Dissertations Publishing, Boston.
[17] Venegas, J.G., Harris, R.S. and Simon, B.A. (1998) A
comprehensive equation for the pulmonary pressure-
volume curve. Journal of Applied Physiology, 84, 389-395.
[18] Thammanomai, A., Majumdar, A., Bartolak-Suki, E. and

S. D. Amin et al. / J. Biomedical Science and Engineering 6 (2013) 61-70 70
Suki, B. (2007) Effects of reduced tidal volume ventila-
tion on pulmonary function in mice before and after acute
lung injury. Journal of Applied Physiology, 103, 1551-
1559.
http://dx.doi.org/10.1152/japplphysiol.00006.2007
[19] Hubmayr, R.D. (2002) Perspective on lung injury and
recruitment: A skeptical look at the opening and collapse
story. American Journal of Respiratory and Critical Care
Medicine, 165, 1647-1653.
http://dx.doi.org/10.1164/rccm.2001080-01CP
[20] Thammanomai, A., Hamakawa, H., Bartolák-Suki, E. and
Suki, B. (2013) Combined effects of ventilation mode
and positive end-expiratory pressure on mechanics, gas
exchange and the epithelium in mice with acute lung in-
jury. PLoS One, 8, Article ID: e53934.
http://dx.doi.org/10.1371/journal.pone.0053934
[21] Wilson, T.A. and Bachofen, H. (1982) A model for me-
chanical structure of the alveolar duct. Journal of Applied
Physiology, 52, 1064-1070.
[22] Stamenovic, D. and Wilson, T.A. (1985) A strain energy
function for lung parenchyma. Journal of Biomechanical
Engineering, 107, 81-86.
http://dx.doi.org/10.1115/1.3138525
[23] Ingenito, E.P., Tsai, L.W., Majumdar, A. and Suki, B.
(2005) On the role of surface tension in the pathophysi-
ology of emphysema. American Journal of Respiratory
and Critical Care Medicine, 171, 300-304.
http://dx.doi.org/10.1164/rccm.200406-770PP
[24] Denny, E. and Schroter, R.C. (1997) Relationships be-
tween alveolar size and fibre distribution in a mammalian
lung alveolar duct model. Journal of Biomechanical En-
gineering, 119, 289-297.
http://dx.doi.org/10.1115/1.2796093
[25] Massa, C.B., Allen, G.B. and Bates, J.H. (2008) Model-
ing the dynamics of recruitment and derecruitment in
mice with acute lung injury. Journal of Applied Physiol-
ogy, 105, 1813-1821.
http://dx.doi.org/10.1152/japplphysiol.90806.2008
[26] Ingenito, E.P., Mark, L., Morris, J., Espinosa, F.F.,
Kamm, R.D. and Johnson, M. (1999) Biophysical char-
acterization and modeling of lung surfactant components.
Journal of Applied Physiology, 86, 1702-1714.
[27] Ghadiali, S.N. and Gaver, D.P. (2008) Biomechanics of
liquid-epithelium interactions in pulmonary airways. Re-
spiratory Physiology & Neurobiology, 163, 232-243.
http://dx.doi.org/10.1016/j.resp.2008.04.008
[28] Amin, S.D., Majumdar, A., Frey, U. and Suki, B. (2009)
Modeling the dynamics of airway constriction: Effects of
agonist transport and binding. Journal of Applied Physi-
ology, 109, 553-563.
http: //dx. doi.o rg/10.1152/ ja ppl physio l.01111. 2009
[29] Wilson, T.A., Anafi, R.C. and Hubmayr, R.D. (2001)
Mechanics of edematous lungs. Journal of Applied Physi-
ology, 90, 2088-2093.
[30] Vlahakis, N.E., Schroeder, M.A., Pagano, R.E. and Hub-
mayr, R.D. (2002) Role of deformation-induced lipid
trafficking in the prevention of plasma membrane stress
failure. American Journal of Respiratory and Critical
Care Medicine, 166, 1282-1289.
http://dx.doi.org/10.1164/rccm.200203-207OC