Effect of cardiac ventricular mechanical contraction on the characteristics of the ECG: A simulation study

doi:10.4236/jbise.2013.612A007

Paper Menu >>

Journal Menu >>

J. Biomedical Science and Engineering, 2013, 6, 47-60 JBiSE

http://dx.doi.org/10.4236/jbise.2013.612A007 Published Online December 2013 (http://www.scirp.org/journal/jbise/)

Effect of cardiac ventricular mechanical contraction on the

characteristics of the ECG: A simulation study

Ismail Adeniran1, Jules C. Hancox2, Henggui Zhang1,3*

1School of Physics and Astronomy, The University of Manchester, Manchester, United Kingdom

2Department of Physiology and Cardiovascular Laboratories, School of Medical Sciences, Bristol, United Kingdom

3School of Computer Sciences and Technology, Harbin Institute of Technology, Harbin, China

Email: *henggui.zhang@Manchester.ac.uk

Received 22 October 2013; revised 25 November 2013; accepted 8 December 2013

which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

Introduction: The 12-lead electrocardiogram (ECG)

is the most widely-used tool for the detection and di-

agnosis of cardiac conditions including myocardial

infarction and ischemia. It has therefore been a focus

of cardiac modeling. However, the most contempo-

rary in silico ECG investigations of the intact heart

have assumed a static heart and ignored the mecha-

nical contraction that is an essential component of

cardiac function. The aim of this study was to utilize

electromechanically coupled human ventricle models

to explore the consequences of ventricular mechanical

contraction on the ECG profiles. Methods and Re-

sults: Biophysically detailed human ventricular cell

models incorporating contractile activity and a stretch-

activated current (Isac) were incorporated into a 3D

human ventricular model within a human torso, from

which 12-lead ECGs were computed at a stimulation

rate of 1 Hz. Compared to the static model, ventricu-

lar contraction without Isac had little effect on the

QRS complex, but shifted the T-wave peak leftwards

and reduced its peak amplitude. With Isac, ventricular

mechanical contraction increased the QRS duration

by 23% and QT interval by 5%. Conclusion: Me-

chanical contraction of the heart has a significant

effect on the morphology and characteristics of the

ECG particularly on the T-wave. The alteration of

the cell membrane kinetics by stretch via Isac further

exacerbates these effects. Our simulation data suggest

that mechanical contraction should be considered in

the interpretation of ECGs in pathological conditions,

especially those in which mechanical contraction of

the heart is impaired.

Keywords: Ventricles; Mechanical Contraction;

Electrophysiology; Simulation; ECG

1. INTRODUCTION

The 12-lead electrocardiogram (ECG) is used to under-

stand a person’s cardiac electrical activity by measuring

the electrical potential on the body surface in order to

obtain diagnostic information on the status of the heart.

Common ECG monitoring’ uses include the detection of

complex arrhythmias, shortened or prolonged QT inter-

vals, ST-segment elevation and ischemia monitoring

[1-3]. The 12-lead ECG system consists of six frontal

plane leads (Lead I, Lead II, Lead III, aVR, aVL and

aVF) and six chest leads (V1 - V6) [1-3]. Though being

the most widely-used cardiac diagnostic tool, the ECG

has some shortcomings, e.g., low sensitivity for detecting

acute inferior myocardial infarction (its sensitivity is

only approximately 60%) [4]. Complex ECG patterns

associated with left bundle branch block (LBBB), ventri-

cular-paced rhythm (VPR) and left ventricular hypertro-

phy (LVH) reduce the ability of the ECG to detect acute

coronary ischemic change and acute myocardial infarc-

tion [5].

Biophysically detailed computer models of the heart

that relate cardiac cellular mechanisms to a clinical mea-

surement of ECG may establish a correlation atlas be-

tween ECG characteristics and various pathological con-

ditions. This may be beneficial for mitigating the short-

comings of the use of clinical ECGs for diagnosing car-

diac diseases. However, the majority of cardiac model-

ling studies have focused mainly on the electrical activity

of the heart, with an assumption that the heart is station-

ary in the thorax [6-10]. This assumption ignores the fact

that the heart is a mechanical pump, which undergoes

rhythmic mechanical contractions in response to cardiac

electrical excitation waves. The mechanical contraction

alters the geometry of the heart as well as the cardiac

*Corresponding author.

OPEN ACCESS

I. Adeniran et al. / J. Biomedical Science and Engineering 6 (2013) 47-60

electrical excitation via the mechanism of mechano-

electric feedback (MEF) [11-14].

It can be anticipated that the motion of the heart dur-

ing the cardiac cycle alters the relative position of the

ECG leads on the body surface to the electrical signal

sources in the heart, as well as the anisotropic conductiv-

ity of the electrical propagation within the torso; all of

which may have influences on the ECG, therefore, pro-

ducing differences to the ECG characteristics is compar-

ed to a stationary heart, particularly during the T-wave

when the heart is subjected to maximum systolic pressure

[2,15]. In addition, in response to changes in volume load

or contractile state (changing geometry), the heart regu-

lates its electrical activity via MEF [11,16,17], which

activates stretch-activated channels (SACs) [18,19] that

regulate cardiac cell action potentials (APs), such as

prolongation or shortening [13,20,21] of AP duration

(APD), changes of AP morphology and AP refractory

properties (such as the diastolic depolarisation and pre-

mature excitation) [11,22-24]. However, it is incomplete-

ly understood how these changes of cardiac geometry

and electrophysiology influence the body surface ECG.

Therefore, the aim of this study was to investigate the

consequences of ventricular wall motion on the 12-lead

ECG in the absence and presence of a stretch-activated

current (Isac) during the cardiac cycle.

2. MATERIAL AND METHODS

2.1. Single Cell Electromechanical Model

For simulating electrophysiology (EP), we utilized the

O’Hara-Rudy (ORd) human ventricular single cell model

[25], which was developed from undiseased human ven-

tricle data and recapitulates human ventricular cell elec-

trical and membrane channel properties, as well as the

transmural heterogeneity of ventricular action potential

(AP) across the ventricular wall [25]. The ORd model

also reproduces Ca2+ versus voltage-dependent inactiva-

tion of L-type Ca2+ current and Ca2+/calmodulin-de-

pendent protein kinase II (CaMK) modulated rate de-

pendence of Ca2+ cycling [25]. For simulating cellular

mechanical properties, we used the Rice et al. myofila-

ment (MM) model [26]. This model was chosen as it is

based on the cross-bridge cycling model of cardiac mus-

cle contraction and is able to replicate a wide range of

experimental data including steady-state force-sarcomere

length (F-SL), force-calcium and sarcomere length-cal-

cium relationships [26].

The intracellular calcium concentration i

Ca 









from the EP model was used as the coupling link to the

MM model. i



produced as dynamic output from

the EP model during the time course of the AP served as

input to the MM model from which the amount of Ca2+

bound to troponin was calculated. The formulation of the

myoplasmic Ca2+ concentration in the EP model is:

Ca 







dCa

cap

iCaipCaCabNaCa imyo

nsr ss

updiff Ca

myo myo

II I





 



 















(1)

where Cai



is the buffer factor for i



, IpCa is the

sarcolemmal Ca2+ pump current, ICab is the Ca2+ back-

ground current, INaCa,i is the myoplasmic component of

Na+/Ca2+ exchange current, Acap is capacitive area, F is

the Faraday constant, vmyo is the volume of the myoplas-

mic compartment, vnsr is the volume of the network sar-

coplasmic reticulum compartment, vss is the volume of

the subspace compartment, Jup is the total Ca2+ uptake

flux, via SERCA pump from myoplasm to the network

sarcoplasmic reticulum and Jdiff,Ca is the flux of the diffu-

sion of Ca2+ from the subspace to the myoplasm.

Ca 





Cai



is formulated as:









,CMDN ,TRPN

CMDN TRPN

Ca Ca

Cai mm





















(2)

where [CMDN] and [TRPN] are the calmodulin and tro-

ponin Ca2+ buffers in the myoplasm respectively, and

Km,CMDN and Km,TRPN are the half-saturation concentra-

tions of calmodulin and troponin respectively.

In the original ORd model, Eq.2 considers Ca2+ bind-

ing to both calmodulin and troponin. However, as the

MM model implements actual regulatory sites for the

apparent Ca2+ binding to troponin, Eq.2 was modified to:





,CMDN

CMDN

Cai m













(3)

Now, the EP model only handles Ca2+ binding to

calmodulin with the MM model handling Ca2+ binding to

troponin. The flux of the binding of Ca2+ to troponin via

the MM model was incorporated into the EP model via

Eq.1 as follows:



dCa

1000

cap

iCaipCaCabNaCa imyo

Trop

nsr ss

updiff Ca

myo myo

II I





 



 









 





(4)



where JTro p is the flux of Ca2+ binding to troponin. The

combination of all state variables from the EP model

I. Adeniran et al. / J. Biomedical Science and Engineering 6 (2013) 47-60 49

with the MM model and the substitution of Eq.3 and

Eq.4 for Eqs.1 and 2 yielded a human ventricular myo-

cyte electromechanical cell model.

2.2. Stretch-Activated Current

In accord with previous studies [19,27-31], we incorpo-

rated a stretch-activated current (Isac) into the electrome-

chanics model using the following formulation:



acsac mmsac

IGPVE (5)

where Gsac and Esac are the maximum channel conduc-

tance and reversal potential of the SAC respectively. In

the electromechanics model, Esac was typically set to

−6.3 mV and describes the experimentally observed de-

polarising effect of the channel [32,33]. Vm is the mem-

brane potential and Pm is the channel’s open probability

modelled as:

1e e



















(6)

where



and



1/2 are the strain (with an explicit depend-

ence on the sarcomere length) and half-activation strain

respectively, ke = 0.02 [19,29,34] is the activation slope.

The SAC is assumed to be permeable to Na+, K+ and

Ca2+ [19,30,35] in the ratio 1:1:1 with Isac therefore de-

fined as:

acsacNasac Ksac Ca

IIII

(7)

where Isac,Na, Isa c,K and Isac,Ca are the contributions of Na+,

K+ and Ca2+ to Isac.

2.3. Tissue Mechanics Model

We modelled cardiac tissue mechanics within the theo-

retical framework of nonlinear elasticity [36,37] as an in-

homogeneous, anisotropic, nearly incompressible nonlin-

ear material similar to previous studies [27,38-42]. We

used a two-field variational principle with the deforma-

tion u and the hydrostatic pressure p as the two fields

[37,43,44]. p is utilised as the Lagrange multiplier to

enforce the near incompressibility constraint. Thus, the

total potential energy functional  for the mechanics

problem is formulated as:







int ext

upup u 



(8)

where





int up is the internal potential energy or

total strain energy of the body and





ext u is the ex-

ternal potential energy or potential energy of the external

loading of the body. As in previous studies [38,41,42,45],

in the absence of body forces, and assuming that the

body is always in instantaneous equilibrium and no iner-

tia effects, the coordinates of the deformed body satisfies

the steady-state equilibrium equation with near incom-

pressibility enforced.

According to standard variational principles, equilib-

rium is derived by searching for critical points of (Eq.8)

in suitable admissible displacement and pressure spaces

and

Uˆ

. The corresponding Euler-Lagrange equa-

tions resulting from (Eq.8) lead to solving the problem

[44,46-49]:

Find (u,p) in ˆˆ



such that:



ˆ,:d

det ˆ

:dd ,

WxId uvx

pIduvxgvsvu





 

U



 





(9)





det1 d0,qIdu xqp





 







ˆˆ

(10)

where and

are the admissible variation spaces

for the displacements and the pressures, respectively.

Id u



 is the deformation gradient, v is a test

function and is the material stored energy function

and corresponds to the density of elastic energy locally

stored in the body during the deformation.

With the axes of the geometry aligned to the underly-

ing tissue microstructure [50,51], the second Piola-

Kirchhoff stress tensor S, obtained from the directional

derivative of (Eq.8) in the direction of an arbitrary vir-

tual displacement and which relates a stress to a strain

measure [37,43] and a manipulation of Eq.9 is defined

as:

Active Tension

2MN

MN NM

SpC















(11)

where W is a strain energy function that defines the con-

stitutive behaviour of the material, E is the Green-La-

grange strain tensor that quantifies the length changes in

a material fibre and angles between fibre pairs in a de-

formed solid, C is the Right-Cauchy green strain tensor,

p is a Lagrange multiplier (referred to as the hydrostatic

pressure in the literature) used to enforce incompressibil-

ity of the cardiac tissue, SActive Tension is a stress tensor in-

corporating active tension from the electromechanics cell

model and enables the reproduction of the three physio-

logical movements of the ventricular wall: longitudinal

shortening, wall thickening and rotational twisting [52-

58].

For the strain energy function W, we used the Guc-

cione constitutive law [59] given by:

1eQ

WC (12)

where







222

2 113223323

41221 1331

QCE CEEE

CEE EE

 



(13)

Following previous work [27,60], ,

10.831 kPaC

I. Adeniran et al. / J. Biomedical Science and Engineering 6 (2013) 47-60

2, 3, 4

14.31C4.49C10C



. ij are the compo-

nents of the Green-Lagrange strain tensor.

2.4. Tissue Electrophysiology Model

The monodomain representation [61-63] of cardiac tissue

was used for the electrophysiology model with a modifi-

cation (the incorporation of the Right Cauchy Green de-

formation tensor C), which allows the monodomain

equation to take into account the effect of the deforming

tissue, similar to previous studies [38,42,64]:



stim

I



DV 



nD V





VENTRICLES



dDCV



 

m ion

t 



(14)

where Cm is the cell capacitance per unit surface area, V

is the membrane potential, Iion is the sum of all trans-

membrane ionic currents from the electromechanics sin-

gle cell model, Istim is an externally applied stimulus and

D is the diffusion tensor. In simulations, intracellular

conductivities in the fibre, cross-fibre and sheet direc-

tions were set to 3.0, 0.1 and 0.31525 ms·mm‒1 respec-

tively. These gave a conduction velocity of 65 cm·s‒1 in

the fibre direction along multiple cells, which is close to

the value 70 cm·s‒1 observed in the fibre direction in

human myocardium [65].

2.5. Tor so Model

The electrical potential in the torso (Figure 1(B)) is ob-

tained via the Poisson equation:



0

(15)

where DT is the torso conductivity and VT is the electrical

potential in the torso. The torso is modelled as a passive

conductor surrounded by air. Consequently, the normal

component of its outer surface is zero leading to the first

boundary condition:

(16)

where n is the outward unit normal on the torso surface,

T is the outer surface of the torso. The torso is a con-

ductor surrounding the ventricles. Therefore, from the

conservation of charge and current, on the boundary be-

tween the ventricles and the torso, the normal component

of the current in the ventricles must equal the normal

component of the current in the surrounding torso. Since

there cannot be a discontinuity in the potentials on the

boundary of two directly connected volume conductors,

i.e., the ventricles and the torso, this condition implies

the following boundary condition:



NTRICLES



 (17)

where VVENTRICLES is the electrical potential on the sur-

face between the ventricles and the torso. The torso con-

ductivity was set to 0.3 ms·mm‒1.

2.6. Computing the 12-Lead ECGs

We computed the ECGs according to the standard defini-

tions [3,66] (Figure 1(B)). The limb leads were calcu-

lated as follows:

Lead

ARA

LRA

III A









where LA, LL and RA refer to the left arm, left leg and

right arm respectively and



X is the potential of the ap-

propriate lead. The augmented limb leads were calcu-

lated as:



Lead Lead

1Lead Lead

aVF III

aVL III

aVRI II



 

The precordial leads, V1 - V6 are located over the left

chest as shown in Figure 1(B). Their potentials are

measured directly from their locations.

2.7. Computational Methods

2.7.1. Ge ometry and Meshes

The 3D simulations were carried out on a DT-MRI re-

constructed anatomical human ventricle geometry (Fig-

ure 1(A)), incorporating anisotropic fibre orientation

(Figure 1(A)), from a healthy 34-year old male. This had

a spatial resolution of 0.2 mm and approximately 24.2

million nodes in total and was segmented into distinct

ENDO (60%), MCELL (30%) and EPI (10%) regions

(Figure 1(A)). The chosen cell proportion in each region

reflects experimental data for cells spanning the left ven-

tricular wall of the human heart [67]. The conditional

activation sites were determined empirically across the

ventricle wall and were validated by reproducing the

activation sequence and QRS complex in the measured

64-channel ECG [68] of that person (Figure 1(A)).

2.7.2. Solving the Electrome chanics Problem

The electromechanics problem consists of two sub-

problems: the electrophysiology problem and the me-

chanics problem. The electrophysiology problem Eq.10

was solved with a Strang splitting method [69] ensuring

that the solution is second-order accurate. It was discre-

tised in time using the Crank-Nicholson method [70],

which is also second-order accurate and discretised in

space with Finite Elements [48,49,70,71]. Iion in Eq.10

epresents the single cell electromechanics model from r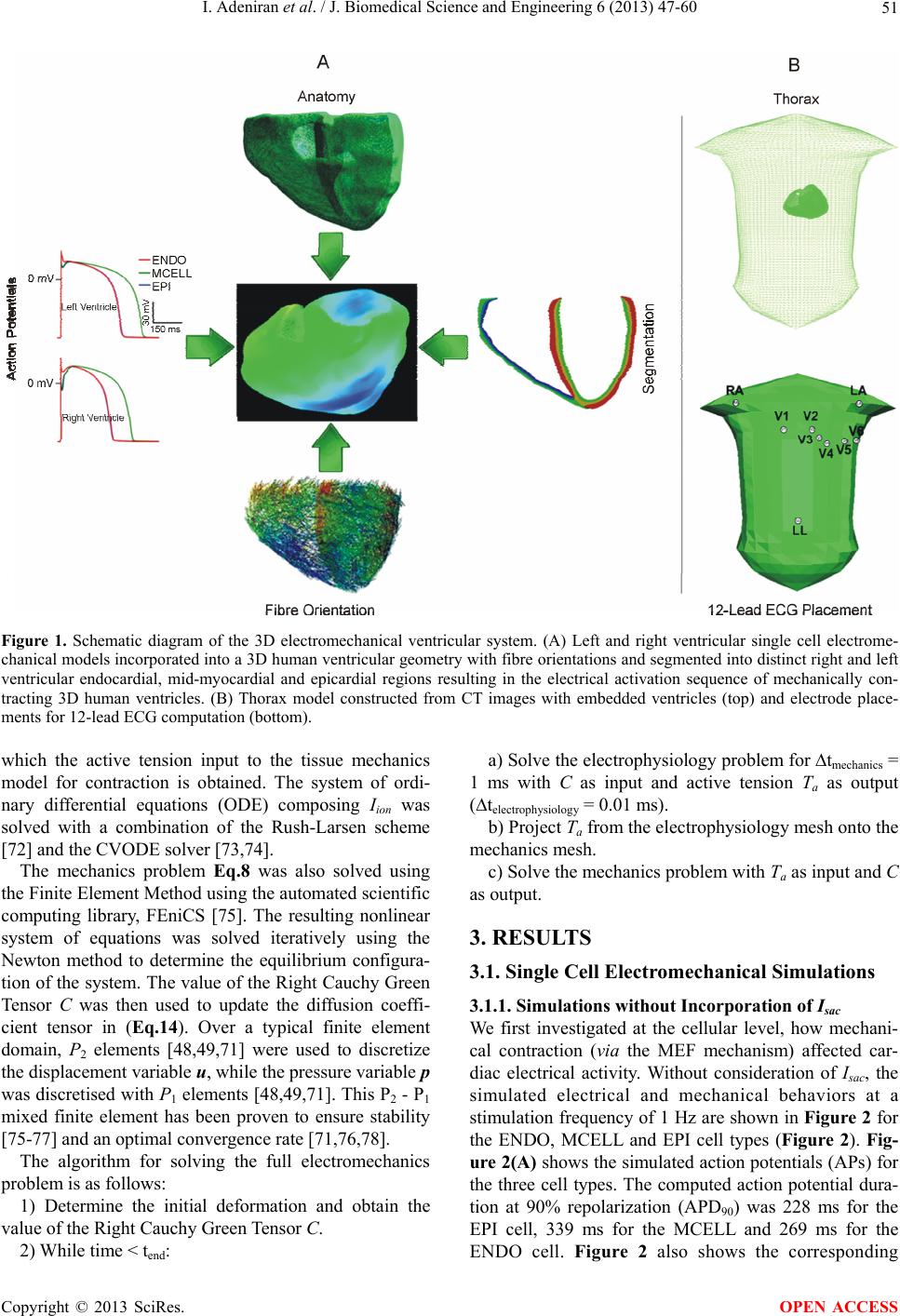

I. Adeniran et al. / J. Biomedical Science and Engineering 6 (2013) 47-60

Figure 1. Schematic diagram of the 3D electromechanical ventricular system. (A) Left and right ventricular single cell electrome-

chanical models incorporated into a 3D human ventricular geometry with fibre orientations and segmented into distinct right and left

ventricular endocardial, mid-myocardial and epicardial regions resulting in the electrical activation sequence of mechanically con-

tracting 3D human ventricles. (B) Thorax model constructed from CT images with embedded ventricles (top) and electrode place-

ments for 12-lead ECG computation (bottom).

which the active tension input to the tissue mechanics

model for contraction is obtained. The system of ordi-

nary differential equations (ODE) composing Iion was

solved with a combination of the Rush-Larsen scheme

[72] and the CVODE solver [73,74].

a) Solve the electrophysiology problem for tmechanics =

1 ms with C as input and active tension Ta as output

(telectrophysiology = 0.01 ms).

b) Project Ta from the electrophysiology mesh onto the

mechanics mesh.

The mechanics problem Eq.8 was also solved using

the Finite Element Method using the automated scientific

computing library, FEniCS [75]. The resulting nonlinear

system of equations was solved iteratively using the

Newton method to determine the equilibrium configura-

tion of the system. The value of the Right Cauchy Green

Tensor C was then used to update the diffusion coeffi-

cient tensor in (Eq.14). Over a typical finite element

domain, P2 elements [48,49,71] were used to discretize

the displacement variable u, while the pressure variable p

was discretised with P1 elements [48,49,71]. This P2 - P1

mixed finite element has been proven to ensure stability

[75-77] and an optimal convergence rate [71,76,78].

c) Solve the mechanics problem with Ta as input and C

as output.

3. RESULTS

3.1. Single Cell Electromechanical Simulations

3.1.1. Si m ulations without I n cor porati on o f Isac

We first investigated at the cellular level, how mechani-

cal contraction (via the MEF mechanism) affected car-

diac electrical activity. Without consideration of Isac, the

simulated electrical and mechanical behaviors at a

stimulation frequency of 1 Hz are shown in Figure 2 for

the ENDO, MCELL and EPI cell types (Figure 2). Fig-

ure 2(A) shows the simulated action potentials (APs) for

the three cell types. The computed action potential dura-

tion at 90% repolarization (APD90) was 228 ms for the

EPI cell, 339 ms for the MCELL and 269 ms for the

ENDO cell. Figure 2 also shows the corresponding

The algorithm for solving the full electromechanics

problem is as follows:

1) Determine the initial deformation and obtain the

value of the Right Cauchy Green Tensor C.

2) While time < tend:

OPEN ACCESS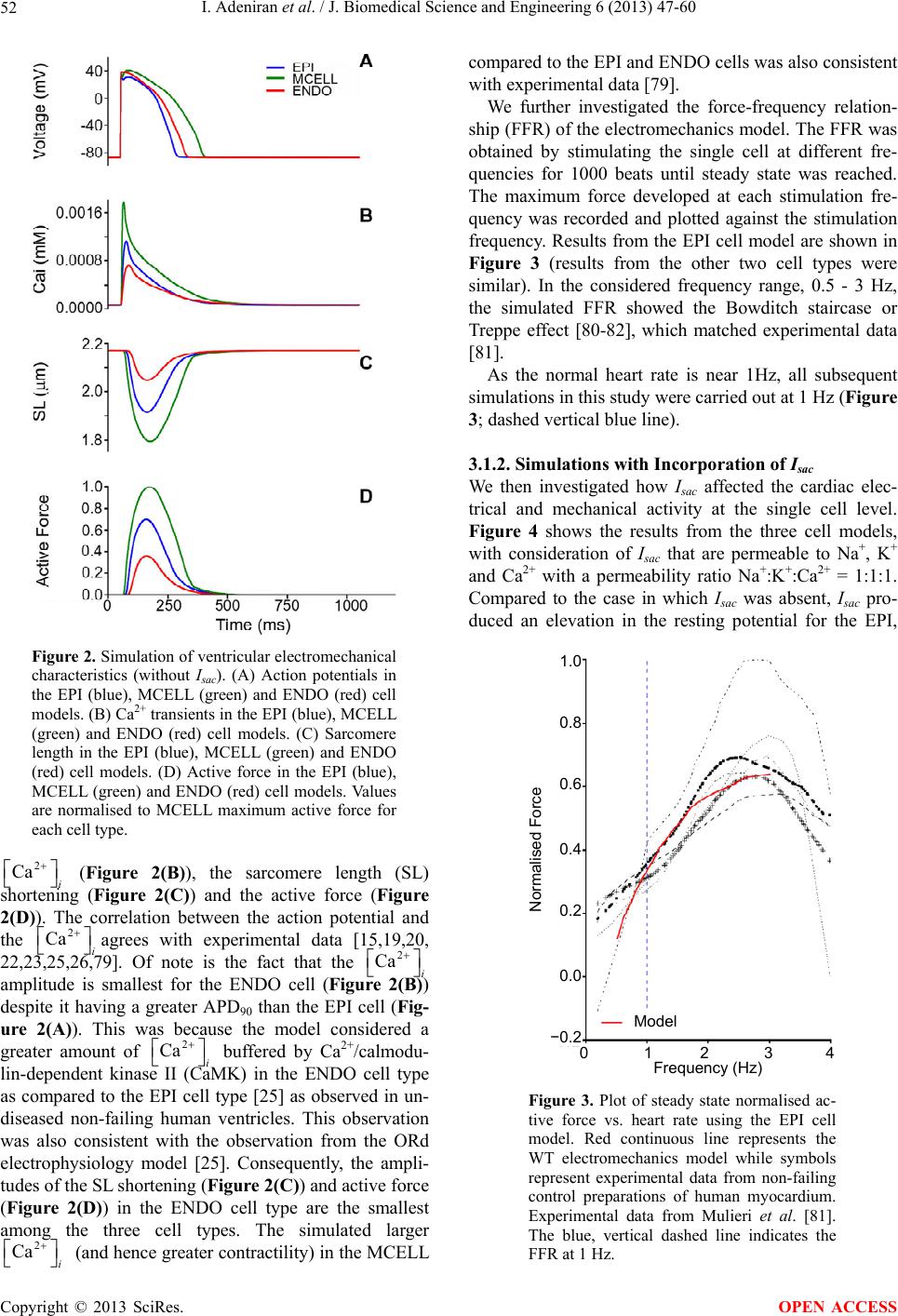

I. Adeniran et al. / J. Biomedical Science and Engineering 6 (2013) 47-60

Figure 2. Simulation of ventricular electromechanical

characteristics (without Isac). (A) Action potentials in

the EPI (blue), MCELL (green) and ENDO (red) cell

models. (B) Ca2+ transients in the EPI (blue), MCELL

(green) and ENDO (red) cell models. (C) Sarcomere

length in the EPI (blue), MCELL (green) and ENDO

(red) cell models. (D) Active force in the EPI (blue),

MCELL (green) and ENDO (red) cell models. Values

are normalised to MCELL maximum active force for

each cell type.

Ca 











(Figure 2(B)), the sarcomere length (SL)

shortening (Figure 2(C)) and the active force (Figure

2(D)). The correlation between the action potential and

the i



agrees with experimental data [15,19,20,

22,23,25,26,79]. Of note is the fact that the i





Ca 









amplitude is smallest for the ENDO cell (Figure 2(B))

despite it having a greater APD90 than the EPI cell (Fig-

ure 2(A)). This was because the model considered a

greater amount of i



buffered by Ca2+/calmodu-

lin-dependent kinase II (CaMK) in the ENDO cell type

as compared to the EPI cell type [25] as observed in un-

diseased non-failing human ventricles. This observation

was also consistent with the observation from the ORd

electrophysiology model [25]. Consequently, the ampli-

tudes of the SL shortening (Figure 2(C)) and active force

(Figure 2(D)) in the ENDO cell type are the smallest

among the three cell types. The simulated larger

(and hence greater contractility) in the MCELL

compared to the EPI and ENDO cells was also consistent

with experimental data [79].

Ca 





We further investigated the force-frequency relation-

ship (FFR) of the electromechanics model. The FFR was

obtained by stimulating the single cell at different fre-

quencies for 1000 beats until steady state was reached.

The maximum force developed at each stimulation fre-

quency was recorded and plotted against the stimulation

frequency. Results from the EPI cell model are shown in

Figure 3 (results from the other two cell types were

similar). In the considered frequency range, 0.5 - 3 Hz,

the simulated FFR showed the Bowditch staircase or

Treppe effect [80-82], which matched experimental data

[81].

As the normal heart rate is near 1Hz, all subsequent

simulations in this study were carried out at 1 Hz (Figure

3; dashed vertical blue line).

3.1.2. Simulations with Incorporation of Isac

We then investigated how Isac affected the cardiac elec-

trical and mechanical activity at the single cell level.

Figure 4 shows the results from the three cell models,

with consideration of Isac that are permeable to Na+, K+

and Ca2+ with a permeability ratio Na+:K+:Ca2+ = 1:1:1.

Compared to the case in which Isac was absent, Isac pro-

duced an elevation in the resting potential for the EPI,

0 1 2 3

Frequency (Hz)

1.0

0.8

0.6

0.4

0.2

0.0

−0.2

Model

Normalised Force



Ca i









Figure 3. Plot of steady state normalised ac-

tive force vs. heart rate using the EPI cell

model. Red continuous line represents the

WT electromechanics model while symbols

represent experimental data from non-failing

control preparations of human myocardium.

Experimental data from Mulieri et al. [81].

The blue, vertical dashed line indicates the

FFR at 1 Hz.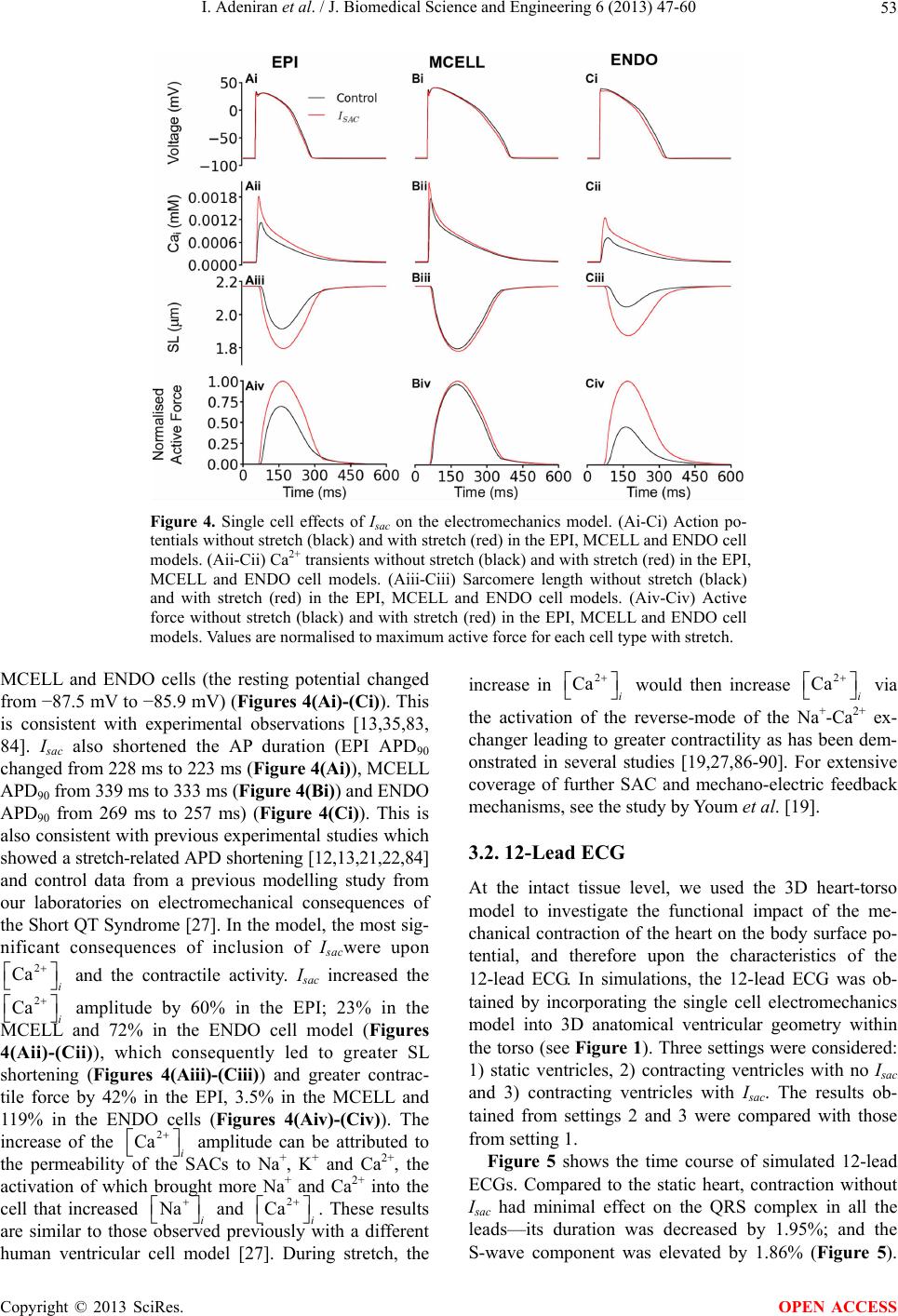

I. Adeniran et al. / J. Biomedical Science and Engineering 6 (2013) 47-60

Figure 4. Single cell effects of Isac on the electromechanics model. (Ai-Ci) Action po-

tentials without stretch (black) and with stretch (red) in the EPI, MCELL and ENDO cell

models. (Aii-Cii) Ca2+ transients without stretch (black) and with stretch (red) in the EPI,

MCELL and ENDO cell models. (Aiii-Ciii) Sarcomere length without stretch (black)

and with stretch (red) in the EPI, MCELL and ENDO cell models. (Aiv-Civ) Active

force without stretch (black) and with stretch (red) in the EPI, MCELL and ENDO cell

models. Values are normalised to maximum active force for each cell type with stretch.

MCELL and ENDO cells (the resting potential changed

from −87.5 mV to −85.9 mV) (Figures 4(Ai)-(Ci)). This

is consistent with experimental observations [13,35,83,

84]. Isac also shortened the AP duration (EPI APD90

changed from 228 ms to 223 ms (Figure 4(Ai)), MCELL

APD90 from 339 ms to 333 ms (Figure 4(Bi)) and ENDO

APD90 from 269 ms to 257 ms) (Figure 4(Ci)). This is

also consistent with previous experimental studies which

showed a stretch-related APD shortening [12,13,21,22,84]

and control data from a previous modelling study from

our laboratories on electromechanical consequences of

the Short QT Syndrome [27]. In the model, the most sig-

nificant consequences of inclusion of Isacwere upon

increase in 2

Ca i









 would then increase via

Ca i









the activation of the reverse-mode of the Na+-Ca2+ ex-

changer leading to greater contractility as has been dem-

onstrated in several studies [19,27,86-90]. For extensive

coverage of further SAC and mechano-electric feedback

mechanisms, see the study by Youm et al. [19].

3.2. 12-Lead ECG

At the intact tissue level, we used the 3D heart-torso

model to investigate the functional impact of the me-

chanical contraction of the heart on the body surface po-

tential, and therefore upon the characteristics of the

12-lead ECG. In simulations, the 12-lead ECG was ob-

tained by incorporating the single cell electromechanics

model into 3D anatomical ventricular geometry within

the torso (see Figure 1). Three settings were considered:

1) static ventricles, 2) contracting ventricles with no Isac

and 3) contracting ventricles with Isac. The results ob-

tained from settings 2 and 3 were compared with those

from setting 1.

Ca i







2









and the contractile activity. Isac increased the



i



amplitude by 60% in the EPI; 23% in the

MCELL and 72% in the ENDO cell model (Figures

4(Aii)-(Cii)), which consequently led to greater SL

shortening (Figures 4(Aiii)-(Ciii)) and greater contrac-

tile force by 42% in the EPI, 3.5% in the MCELL and

119% in the ENDO cells (Figures 4(Aiv)-(Civ)). The

increase of the i



amplitude can be attributed to

the permeability of the SACs to Na+, K+ and Ca2+, the

activation of which brought more Na+ and Ca2+ into the

cell that increased i



and i



. These results

are similar to those observed previously with a different

human ventricular cell model [27]. During stretch, the

Ca 





Na



2

Ca 





Figure 5 shows the time course of simulated 12-lead

ECGs. Compared to the static heart, contraction without

Isac had minimal effect on the QRS complex in all the

leads—its duration was decreased by 1.95%; and the

S-wave component was elevated by 1.86% (Figure 5).

OPEN ACCESS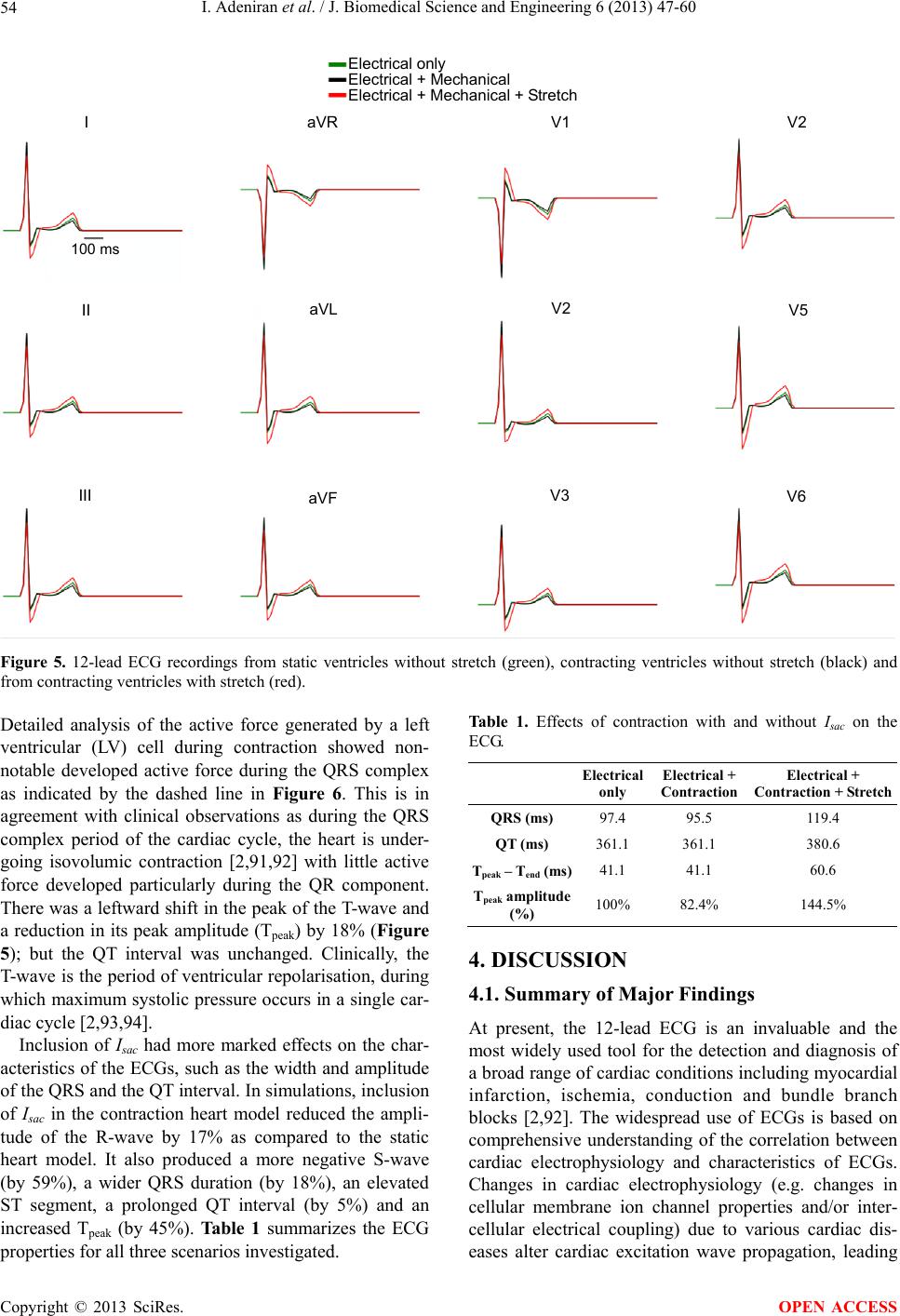

I. Adeniran et al. / J. Biomedical Science and Engineering 6 (2013) 47-60

Electrical only

Electrical + Mechanical

Electrical + Mechanical + Stretch

III

aVR

aVL

aVF V3

V1 V2

100 ms

Figure 5. 12-lead ECG recordings from static ventricles without stretch (green), contracting ventricles without stretch (black) and

from contracting ventricles with stretch (red).

Detailed analysis of the active force generated by a left

ventricular (LV) cell during contraction showed non-

notable developed active force during the QRS complex

as indicated by the dashed line in Figure 6. This is in

agreement with clinical observations as during the QRS

complex period of the cardiac cycle, the heart is under-

going isovolumic contraction [2,91,92] with little active

force developed particularly during the QR component.

There was a leftward shift in the peak of the T-wave and

a reduction in its peak amplitude (Tpeak) by 18% (Figure

5); but the QT interval was unchanged. Clinically, the

T-wave is the period of ventricular repolarisation, during

which maximum systolic pressure occurs in a single car-

diac cycle [2,93,94].

Inclusion of Isac had more marked effects on the char-

acteristics of the ECGs, such as the width and amplitude

of the QRS and the QT interval. In simulations, inclusion

of Isac in the contraction heart model reduced the ampli-

tude of the R-wave by 17% as compared to the static

heart model. It also produced a more negative S-wave

(by 59%), a wider QRS duration (by 18%), an elevated

ST segment, a prolonged QT interval (by 5%) and an

increased Tpeak (by 45%). Ta b l e 1 summarizes the ECG

properties for all three scenarios investigated.

Table 1. Effects of contraction with and without Isac on the

ECG.

Electrical

only

Electrical +

Contraction

Electrical +

Contraction + Stretch

QRS (ms) 97.4 95.5 119.4

QT (ms) 361.1 361.1 380.6

Tpeak – Tend (ms)41.1 41.1 60.6

Tpeak amplitude

(%) 100% 82.4% 144.5%

4. DISCUSSION

4.1. Summary of Major Findings

At present, the 12-lead ECG is an invaluable and the

most widely used tool for the detection and diagnosis of

a broad range of cardiac conditions including myocardial

infarction, ischemia, conduction and bundle branch

blocks [2,92]. The widespread use of ECGs is based on

comprehensive understanding of the correlation between

cardiac electrophysiology and characteristics of ECGs.

Changes in cardiac electrophysiology (e.g. changes in

cellular membrane ion channel properties and/or inter-

cellular electrical coupling) due to various cardiac dis-

eases alter cardiac excitation wave propagation, leading

I. Adeniran et al. / J. Biomedical Science and Engineering 6 (2013) 47-60 55

Electrical only

Electrical + Mechanical

Electrical + Mechanical + Stretch

100 ms

Figure 6. ECG and active force recordings from a left

ventricular cell in static ventricles without stretch

(green), contracting ventricles without stretch (black)

and from contracting ventricles with stretch (red).

to an altered electrical field in and around the heart that

varies with time during the cardiac cycle [2,15,92]. Such

a changed electrical field surrounding the heart is re-

flected by changes in the ECG characteristics. Another

important characteristic of the heart is the muscle con-

traction and relaxation, which also varies with time dur-

ing the cardiac cycle [2,15,92]. In addition, in response

to mechanical events such as stretch and volume load,

the heart regulates its own electrical activity via MEF

[2,18,19]; which includes the activation of SACs [18,19,

95]. So far, how cardiac mechanical contraction influ-

ences ECG characteristics is less well-understood. In the

present study, we have incorporated biophysically de-

tailed coupled electromechanical ventricular cell models

into a 3D-anatomical human ventricle situated within a

human thorax to investigate the effects of mechanical

contraction with and without Isac on the 12-lead ECG.

Our simulations suggest that: 1) contraction without con-

sideration of Isac has no significant effect on the QRS

complex, no effect on the QT interval, but shifts the

T-wave leftwards and reduces Tpeak (Figure 5); 2) con-

traction with consideration of Isac reduces the R-wave

amplitude, widens the QRS complex duration, increases

Tpeak significantly, shifts the T-wave rightwards and in-

creases the QT interval (Figure 5). These findings are

dependent on the degree of stretch and are influenced by

the magnitude of Isac. Several aspects of our findings

merit more detailed discussion.

4.2. Mechanistic Insights

With mechanically contracting ventricles without con-

sideration of Isac, the QRS complex was not affected sig-

nificantly, either in duration (1.95% decrease) or mor-

phology (Figure 5). Contraction during the QRS com-

plex is isovolumic [2,91,92], thus explaining the insig-

nificant effect of contraction on the ECG during this pe-

riod. Contraction of each myocyte in the intact tissue is

not necessarily isometric, however, as each undergoes

different length changes with time. Some myocytes con-

tract isotonically, some isometrically whilst others con-

tract eccentrically [2,91,92,94]. Therefore, even though

the ventricular volume does not change substantially, the

ventricle chamber geometry changes considerably [2,94,

96-98]. Consequently, compared to a static heart, the

position of the cardiac electrical sources, the distance of

the ventricles from the body surface and the varying

anisotropic conductivity due to MEF are altered in a

mechanically contracting heart; hence, there was a 1.95%

decrease in QRS duration without Isac. With considera-

tion of Isac, these differential changes in myocyte lengths

and hence ventricular geometry are exacerbated; hence,

there was a greater and more significant effect of con-

traction with Isac on the QRS complex (Figure 5). By the

Frank-Starling law, with the increased stretch of the

myocardial fibers during diastole by Isac, contractility

would increase [2,94,99].

During the T-wave, ventricular contraction attains a

maximum, after which ventricular pressure declines with

ventricular repolarisation causing a decline in the active

force of the myocytes [2,94,96-98]. The ventricular

pressure during this period is ~30% greater than during

the QRS complex [2,94,96-98]. Therefore, during con-

traction, the aforementioned changes in ventricular ge-

ometry, the distance of the ventricles from the body sur-

face and the varying anisotropic conductivity due to

MEF are altered markedly compared to a static heart.

This results in a marked effect on the T-wave; without

Isac, it is shifted leftwards and the Tpeak is reduced in am-

plitude by 18%. With Isac, the myocardial fibers are

stretched during diastole leading to increased contractil-

ity, which in turn increases systolic pressure [2,94,99]

leading to a greater effect on the T-wave (Figure 5); Tpeak

is increased in amplitude significantly by ~45% and QT

I. Adeniran et al. / J. Biomedical Science and Engineering 6 (2013) 47-60

interval is increased by ~5%.

4.3. Relevance to Previous Studies

Our simulations suggest that ventricular contraction al-

ters 12-lead ECG morphology. This is consistent with

previous studies [100-103]. In their study, Wei et al. [100]

used MRI time sequences of the motion of a human ven-

tricular geometry to compute 12-lead ECGs by mounting

the geometry in a model of the human body. They found

that ventricular motion reduced Tpeak with minimal

change to the QRS complex. However, they did not con-

sider the incorporation of Isac. Xia et al. [101] also ob-

tained similar results with a human whole heart geometry

mounted in a human torso but their simulations lacked

the use of biophysically detailed electromechanical sin-

gle cell models and the incorporation of Isac. Therefore,

the present work is the first study to investigate the ef-

fects of Isac on the characteristics of simulated body sur-

face 12-lead ECGs using anatomically detailed and me-

chanically contracting ventricles. The findings from the

present study improve our understanding of the effects of

electrical-mechanical coupling on the characteristics of

ECG. This was achieved by 1) using biophysically de-

tailed human ventricular myocyte models [25] coupled

with the Rice et al. myofilament model [26]; employed

with and without Isac and 2) by demonstrating the impor-

tance of ventricular motion on the morphology, proper-

ties and subsequently interpretation of the 12 lead ECG.

4.4. Limitations

In addition to acknowledged limitations of both the ORd

electrophysiology model [25] and the Rice et al. [26]

myofilament model, Isac density was based on prior stud-

ies [19,28-31], due to lack of experimental data on the

Isac from human ventricular myocytes. Additionally, the

simulations here were performed at a single, physiologi-

cally relevant frequency (1 Hz), but rate-dependent dif-

ferences in MEF have not been pursued in this initial

study Experimentally observed effects of cycle length

(restitution curve) [104] have also not been studied.

These rate-dependent phenomena would constitute a val-

uable future line of investigation. It should also be ac-

knowledged that Isac. may not be the only mechanism

responsible for MEF (e.g. [105]) and that due to an ab-

sence of functional data in human myocytes, the elec-

tromechanical model lacks stretch sensitive K+ channels

(e.g. TREK). The model also lacks interactions between

myocytes and fibroblasts, which have been proposed to

contribute to ventricular MEF [106,107]. Whilst it would

be useful for such components to be incorporated into

future models, the advantage of the approach adopted

here is that it has been possible to isolate and attribute

with confidence electrical changes to the incorporation of

Isac. Finally, the use of a ventricular computational fluid

dynamics model to determine pressure boundary condi-

tions would allow a more realistic pressure profile. Al-

though it is important that these potential limitations are

stated, they do not fundamentally influence the principal

conclusions of this study.

5. CONCLUSION

With the use of a biophysically detailed electromechani-

cal human ventricular single cell model incorporated into

a thorax-mounted human ventricular geometry, we have

shown that the morphology and properties of the ECG

are dependent on ventricular contraction. We have also

shown that cellular stretch incorporated at the single cell

level as an SAC has a significant influence on the ECG

in a mechanically contracting ventricle.

6. ACKNOWLEDGEMENTS

This work was supported by project grants from Engineering and

Physical Science Research Council UK (EP/J00958X/1; EP/I029826/1),

the British Heart Foundation (FS/08/021), the Natural Science Founda-

tion of China (61179009) and the University of Manchester.

REFERENCES

[1] Drew, B.J., Califf, R.M., Funk, M., Kaufman, E.S., Kru-

coff, M.W., Laks, M.M., Macfarlane, P.W., Sommargren,

C., Swiryn, S., Van Hare, G.F. and American Heart As-

sociation (2005) AHA scientific statement: Practice stan-

dards for electrocardiographic monitoring in hospital set-

tings: An American Heart Association Scientific State-

ment from the Councils on Cardiovascular Nursing,

Clinical Cardiology, and Cardiovascular Disease in the

Young: Endorsed by the International Society of Com-

puterized electrocardiology and the American Associa-

tion of Critical-Care Nurses. Journal of Cardiovascular

Nursing, 20, 76-106.

http://dx.doi.org/10.1097/00005082-200503000-00003

[2] Bonow, R.O., Mann, D.L., Zipes, D.P. and Libby, P.

(2011) Braunwald’s heart disease: A textbook of cardio-

vascular medicine, 2-volume set: Expert consult premium

edition-enhanced online features and print. 9th Edition,

Saunders.

[3] Malmivuo, J. and Plonsey, R. (1995) Bioelectromagnet-

ism: principles and applications of bioelectric and bio-

magnetic fields. Oxford University Press, New York.

http://dx.doi.org/10.1093/acprof:oso/9780195058239.001

.0001

[4] Menown, I.B., Mackenzie, G. and Adgey, A.A. (2000)

Optimizing the initial 12-lead electrocardiographic diag-

nosis of acute myocardial infarction. European Heart

Journal, 21, 275-283.

ttp://dx.doi.org/10.1053/euhj.1999.1748

[5] Brady, W.J., Chan, T.C. and Pollack, M. (2000) Electro-

cardiographic manifestations: Patterns that confound the

EKG diagnosis of acute myocardial infarction-left bundle

I. Adeniran et al. / J. Biomedical Science and Engineering 6 (2013) 47-60 57

branch block, ventricular paced rhythm, and left ventri-

cular hypertrophy. Journal of Emergency Medicine, 18,

71-78. http://dx.doi.org/10.1016/S0736-4679(99)00178-X

[6] Sovilj, S., Magjarevic, R., Lovell, N.H. and Dokos, S.

(2013) A simplified 3D model of whole heart electrical

activity and 12-lead ECG generation. Computational and

Mathematical Methods in Medicine, 2013, Article ID:

134208.

[7] Keller, D.U.J, Seemann, G., Weiss, D.L., Farina, D., Ze-

helein, J. and Dossel, O. (2007) Computer based model-

ing of the congenital long-QT 2 syndrome in the Visible

Man torso: From genes to ECG. Proceedings of the 29th

Annual International Conference of the IEEE EMBS,

Lyon, 23-26 August 2007, 1410-1413.

[8] Boulakia, M., Cazeau, S., Fernández, M.A., Gerbeau, J.-F.

and Zemzemi, N. (2010) Mathematical modeling of elec-

trocardiograms: A numerical study. Annals of Biomedical

Engineering, 38, 1071-1097.

http://dx.doi.org/10.1007/s10439-009-9873-0

[9] Potse, M., Dubé, B. and Vinet, A. (2009) Cardiac anisot-

ropy in boundary-element models for the electrocardio-

gram. Medical & Biological Engineering & Computing,

47, 719-729.

http://dx.doi.org/10.1007/s11517-009-0472-x

[10] Potse, M., Dube, B. and Gulrajani, R.M. (2003) ECG

simulations with realistic human membrane, heart, and

torso models. Proceedings of the 25th Annual Interna-

tional Conference of the IEEE EMBS, Cancun, 17-21

September 2003, 70-73.

[11] Lab, M.J. (1996) Mechanoelectric feedback (transduction)

in heart: Concepts and implications. Cardiovascular Re-

search, 32, 3-14.

[12] Taggart, P. (1996) Mechano-electric feedback in the hu-

man heart. Cardiov a scular Research, 32, 38-43.

[13] Taggart, P. and Sutton, P.M. (1999) Cardiac mechano-

electric feedback in man: Clinical relevance. Progress in

Biophysics and Molecular Biology, 71, 139-154.

http://dx.doi.org/10.1016/S0079-6107(98)00039-X

[14] Kelly, D., Mackenzie, L., Hunter, P., Smaill, B. and Saint,

D.A. (2006) Gene expression of stretch-activated chan-

nels and mechanoelectric feedback in the heart. Clinical

and Experimental Pharmacology and Physiology, 33,

642-648.

http://dx.doi.org/10.1111/j.1440-1681.2006.04392.x

[15] Katz, A. (2010) Physiology of the heart. 5th Edition,

Lippincott Williams & Wilkins, Philadelphia.

[16] Franz, M.R. (1996) Mechano-electrical feedback in ven-

tricular myocardium. Cardiovascular Research, 32, 15-

24.

[17] Lab, M.J. (1982) Contraction-excitation feedback in myo-

cardium. Physiological basis and clinical relevance. Cir-

culation Research, 50, 757-766.

http://dx.doi.org/10.1161/01.RES.50.6.757

[18] Ward, M.-L. and Allen, D.G. (2010) Stretch-activated

channels in the heart: Contribution to cardiac perform-

ance. In: Kamkin, A. and Kiseleva, I., Ed., Mechanosen-

sitivity of the Heart Mechanosensitivity in Cells and Tis-

sues, Springer, Dordrecht, 141-167.

[19] Youm, J.B., Han, J., Kim, N., Zhang, Y.-H., Kim, E.,

Leem, C.H., Kim, S.H. and Earm, Y.E. (2005) Role of

stretch-activated channels in the heart: Action potential

and Ca2+ transients. In: Kamkin, A. and Kiseleva, I., Ed.,

Mechanosensitivity in Cells and Tissues, Academia, Mos-

cow.

[20] Belus, A. and White, E. (2003) Streptomycin and intra-

cellular calcium modulate the response of single guinea-

pig ventricular myocytes to axial stretch. The Journal of

Physiology, 546, 501-509.

http://dx.doi.org/10.1113/jphysiol.2002.027573

[21] Zeng, T., Bett, G.C. and Sachs, F. (2000) Stretch-activat-

ed whole cell currents in adult rat cardiac myocytes.

American Journal of Physiology. Heart and Circulatory

Physiology, 278, H548-H557.

[22] Dean, J.W. and Lab, M.J. (1989) Effect of changes in

load on monophasic action potential and segment length

of pig heart in situ. Cardiovascular Research, 23, 887-

896. http://dx.doi.org/10.1093/cvr/23.10.887

[23] Franz, M.R., Burkhoff, D., Yue, D.T. and Sagawa, K.

(1989) Mechanically induced action potential changes

and arrhythmia in isolated and in situ canine hearts. Car-

diovascular Research, 23, 213-223.

http://dx.doi.org/10.1093/cvr/23.3.213

[24] Hansen, D.E. (1993) Mechanoelectrical feedback effects

of altering preload, afterload, and ventricular shortening.

American Journal of Physiology, 264, H423-H432.

[25] O’Hara, T., Virág, L., Varró, A. and Rudy, Y. (2011)

Simulation of the undiseased human cardiac ventricular

action potential: Model formulation and experimental

validation. PLOS Computational Biology, 7, Article ID:

e1002061.

http://dx.doi.org/10.1371/journal.pcbi.1002061

[26] Rice, J.J., Wang, F., Bers, D.M. and de Tombe, P.P.

(2008) Approximate model of cooperative activation and

crossbridge cycling in cardiac muscle using ordinary dif-

ferential equations. Biophysical Journal, 95, 2368-2390.

http://dx.doi.org/10.1529/biophysj.107.119487

[27] Adeniran, I., Hancox, J. and Zhang, H. (2013) In silico

investigation of the short QT syndrome, using human

ventricle models incorporating electromechanical coupl-

ing. Front Physiology, 4, 166.

[28] Panfilov, A.V., Keldermann, R.H. and Nash, M.P. (2005)

Self-organized pacemakers in a coupled reaction-diffu-

sion-mechanics system. Physical Review Letters, 95, Ar-

ticle ID: 258104.

http://dx.doi.org/10.1103/PhysRevLett.95.258104

[29] Lunze, K., Stålhand, J. and Leonhardt, S. (2010) Model-

ing of stretch-activated sarcolemmal channels in smooth

muscle cells. Proceedings of the World Congress on Me-

dical Physics and Biomedical Engineering IFMBE, Mu-

nich, 7-12 September 2009, 740-743.

[30] Kuijpers, N.H.L. (2008) Cardiac electrophysiology and

mechanoelectric feedback. Ph.D. Thesis, Eindhoven Uni-

versity of Technology, Eindhoven.

[31] Kohl, P. and Sachs, F. (2001) Mechanoelectric feedback

in cardiac cells. Philosophical Transactions of the Royal

Society A, 359, 1173-1185.

http://dx.doi.org/10.1098/rsta.2001.0824

I. Adeniran et al. / J. Biomedical Science and Engineering 6 (2013) 47-60

[32] Trayanova, N., Li, W., Eason, J. and Kohl, P. (2004)

Effect of stretch-activated channels on defibrillation effi-

cacy. Heart Rhythm, 1, 67-77.

http://dx.doi.org/10.1016/j.hrthm.2004.01.002

[33] Kohl, P., Hunter, P. and Noble, D. (1999) Stretch-induced

changes in heart rate and rhythm: Clinical observations,

experiments and mathematical models. Progress in Bio-

physics and Molecular Biology, 71, 91-138.

http://dx.doi.org/10.1016/S0079-6107(98)00038-8

[34] Zabel, M., Koller, B.S., Sachs, F. and Franz, M.R. (1996)

Stretch-induced voltage changes in the isolated beating

heart: importance of the timing of stretch and implica-

tions for stretch-activated ion channels. Cardiovascular

Research, 32, 120-130.

[35] Kamkin, A., Kiseleva, I. and Isenberg, G. (2000) Stretch-

activated currents in ventricular myocytes: Amplitude

and arrhythmogenic effects increase with hypertrophy.

Cardiovascular Research, 48, 409-420.

http://dx.doi.org/10.1016/S0008-6363(00)00208-X

[36] Marsden, J.E. and Hughes, T.J.R. (1994) Mathematical

foundations of elasticity. Dover Publications, New York.

[37] Holzapfel, G.A. (2000) Nonlinear solid mechanics: A

continuum approach for engineering. John Wiley & Sons

Ltd., Chichester.

[38] Pathmanathan, P. and Whiteley, J.P. (2009) A numerical

method for cardiac mechanoelectric simulations. Annals

of Biomedical Engineering, 37, 860-873.

http://dx.doi.org/10.1007/s10439-009-9663-8

[39] Costa, K.D., Holmes, J.W. and Mcculloch, A.D. (2001)

Modelling cardiac mechanical properties in three dimen-

sions. Philosophical Transactions of the Royal Society A,

359, 1233-1250. http://dx.doi.org/10.1098/rsta.2001.0828

[40] Hunter, P.J., Nash, M.P. and Sands, G.B. (1997) Compu-

tational mechanics of the heart. In: Panfilov, A.V. and

Holden, A.V., Eds., Computational Biology of the Heart.

Wiley, West Sussex, 345-407.

[41] Niederer, S.A. and Smith, N.P. (2008) An improved nu-

merical method for strong coupling of excitation and

contraction models in the heart. Progress in Biophysics

and Molecular Biology, 96, 90-111.

http://dx.doi.org/10.1016/j.pbiomolbio.2007.08.001

[42] Whiteley, J.P., Bishop, M.J. and Gavaghan, D.J. (2007)

Soft tissue modelling of cardiac fibres for use in coupled

mechano-electric simulations. Bulletin of Mathematical

Biology, 69, 2199-2225.

http://dx.doi.org/10.1007/s11538-007-9213-1

[43] Bonet, J. and Wood, R.D. (2008) Nonlinear continuum

mechanics for finite element analysis. 2nd Edition, Cam-

bridge University Press, Cambridge.

http://dx.doi.org/10.1017/CBO9780511755446

[44] Le Tallec, P. (1994) Numerical methods for nonlinear

three-dimensional elasticity. In: Lions, J.L. and Ciarlet,

P.G., Eds., Handbook of Numerical Analysis; Vol.3, Tech-

niques of Scientific Computing (part 1); Numerical Meth-

ods for Solids (part 1); Solution of Equations in R(n) (part

2), North-Holland, London.

[45] Keldermann, R.H., Nash, M.P. and Panfilov, A.V (2009)

Modeling cardiac mechano-electrical feedback using re-

action-diffusion-mechanics systems. Physica D: Nonlin-

ear Phenomena, 238, 1000-1007.

http://dx.doi.org/10.1016/j.physd.2008.08.017

[46] Auricchio, F., Beirão da Veiga, L., Lovadina, C. and Rea-

li, A. (2010) The importance of the exact satisfaction of

the incompressibility constraint in nonlinear elasticity:

Mixed FEMs versus NURBS-based approximations. Com-

puter Methods in Applied Mechanics and Engineering,

199, 314-323.

http://dx.doi.org/10.1016/j.cma.2008.06.004

[47] Braess, D. and Ming, P. (2005) A finite element method

for nearly incompressible elasticity problems. Math

Comp, 74, 25-52.

http://dx.doi.org/10.1090/S0025-5718-04-01662-X

[48] Braess, D. (2007) Finite elements: Theory, fast solvers,

and applications in solid mechanics. 3rd Edition, Cam-

bridge University Press, Cambridge.

http://dx.doi.org/10.1017/CBO9780511618635

[49] Brenner, S.C. and Scott, R. (2010) The mathematical

theory of finite element methods. 3rd Edition, Springer,

New York.

[50] Seemann, G., Keller, D.U.J., Weiss, D.L. and Dössel, O.

(2006) Modeling human ventricular geometry and fiber

orientation based on diffusion tensor MRI. Computers in

Cardiology, 33, 801-804.

[51] Legrice, I.J., Hunter, P.J. and Smaill, B.H. (1997) Lami-

nar structure of the heart: A mathematical model. The

American Journal of Physiology, 272, H2466-H2476.

[52] Lilli, A., Baratto, M.T., Meglio, J.D., Chioccioli, M., Mag-

nacca, M., Talini, E., Canale, M.L., Poddighe, R., Co-

mella, A. and Casolo, G. (2013) Left ventricular rotation

and twist assessed by four-dimensional speckle tracking

echocardiography in healthy subjects and pathological

remodeling: A single center experience. Echocardiogra-

phy, 30, 171-179.

http://dx.doi.org/10.1111/echo.12026

[53] Lorenz, C.H., Pastorek, J.S. and Bundy, J.M. (2000) De-

lineation of normal human left ventricular twist through-

out systole by tagged cine magnetic resonance imaging.

Journal of Cardiovascular Magnetic Resonance, 2, 97-

108. http://dx.doi.org/10.3109/10976640009148678

[54] Tseng, W-Y.I., Reese, T.G., Weisskoff, R.M., Brady, T.J.

and Wedeen, V.J. (2000) Myocardial fiber shortening in

humans: Initial results of MR imaging. Radiology , 216,

128-139.

http://dx.doi.org/10.1148/radiology.216.1.r00jn39128

[55] MacGowan, G.A., Shapiro, E.P., Azhari, H., Siu, C.O.,

Hees, P.S., Hutchins, G.M., Weiss, J.L. and Rademakers,

F.E. (1997) Noninvasive measurement of shortening in

the fiber and cross-fiber directions in the normal human

left ventricle and in idiopathic dilated cardiomyopathy.

Circulation, 96, 535-541.

http://dx.doi.org/10.1161/01.CIR.96.2.535

[56] Coppola, B.A. and Omens, J.H. (2008) Role of tissue

structure on ventricular wall mechanics. MCB Molecular

and Cellular Biomechanics, 5, 183-196.

[57] Cheng, A., Nguyen, T.C., Malinowski, M., Daughters,

G.T., Miller, D.C. and Ingels Jr., N.B. (2008) Heteroge-

neity of left ventricular wall thickening mechanisms. Cir-

I. Adeniran et al. / J. Biomedical Science and Engineering 6 (2013) 47-60 59

culation, 118, 713-721.

http://dx.doi.org/10.1161/CIRCULATIONAHA.107.7446

[58] Bogaert, J. and Rademakers, F.E. (2001) Regional non-

uniformity of normal adult human left ventricle. Ameri-

can Journal of Physiology. Heart and Circulatory Physi-

ology, 280, H610-H620.

[59] Guccione, J.M., McCulloch, A.D. and Waldman, L.K.

(1991) Passive material properties of intact ventricular

myocardium determined from a cylindrical model. Jour-

nal of Biomechanical Engineering, 113, 42-55.

http://dx.doi.org/10.1115/1.2894084

[60] Land, S., Niederer, S.A. and Smith, N.P. (2012) Efficient

computational methods for strongly coupled cardiac elec-

tromechanics. IEEE Transactions on Biomedical Engi-

neering, 59, 1219-1228.

http://dx.doi.org/10.1109/TBME.2011.2112359

[61] Colli Franzone, P., Pavarino, L.F. and Taccardi, B. (2005)

Simulating patterns of excitation, repolarization and ac-

tion potential duration with cardiac bidomain and mo-

nodomain models. Mathematical Biosciences, 197, 35-66.

http://dx.doi.org/10.1016/j.mbs.2005.04.003

[62] Potse, M., Dubé, B., Richer, J., Vinet, A. and Gulrajani,

R.M. (2006) A comparison of monodomain and bidomain

reaction-diffusion models for action potential propagation

in the human heart. IEEE Transactions on Biomedical

Engineering, 53, 2425-2435.

http://dx.doi.org/10.1109/TBME.2006.880875

[63] Keener, J. and Sneyd, J. (2008) Mathematical physiology:

II: Systems physiology. 2nd Edition, Springer, New York.

[64] Nash, M.P. and Panfilov, A.V. (2004) Electromechanical

model of excitable tissue to study reentrant cardiac arrhy-

thmias. Progress in Biophysics and Molecular Biology,

85, 501-522.

http://dx.doi.org/10.1016/j.pbiomolbio.2004.01.016

[65] Taggart, P., Sutton, P.M., Opthof, T., Coronel, R., Trim-

lett, R., Pugsley, W. and Kallis, P. (2000) Inhomogeneous

transmural conduction during early ischaemia in patients

with coronary artery disease. Journal of Molecular and

Cellular Cardiology, 32, 621-630.

http://dx.doi.org/10.1006/jmcc.2000.1105

[66] Plonsey, R. and Barr, R.C. (2007) Bioelectricity: A quan-

titative approach. 3rd Edition, Springer, New York.

[67] Drouin, E., Charpentier, F., Gauthier, C., Laurent, K. and

Le Marec, H. (1995) Electrophysiologic characteristics of

cells spanning the left ventricular wall of human heart:

Evidence for presence of M cells. Journal of the Ameri-

can College of Cardiology, 26, 185-192.

http://dx.doi.org/10.1016/0735-1097(95)00167-X

[68] Keller, D.U.J., Kalayciyan, R., Dössel, O. and Seemann,

G. (2009) Fast creation of endocardial stimulation pro-

files for the realistic simulation of body surface ECGs.

Proceedings of the World Congress on Medical Physics

and Biomedical Engineering IFMBE, Munich, 7-12 Sep-

tember 2009, 145-148.

[69] Sundnes, J., Lines, G.T. and Tveito, A. (2005) An opera-

tor splitting method for solving the bidomain equations

coupled to a volume conductor model for the torso. Ma-

thematical Biosciences, 194, 233-248.

http://dx.doi.org/10.1016/j.mbs.2005.01.001

[70] Burnett, D.S. (1987) Finite element analysis: From con-

cepts to applications. Addison Wesley, Massachusetts.

[71] Ern, A. and Guermond, J.L. (2010) Theory and practice

of finite elements. Springer, New York.

[72] Rush, S. and Larsen, H. (1978) A practical algorithm for

solving dynamic membrane equations. IEEE Transac-

tions on Biomedical Engineering, 25, 389-392.

http://dx.doi.org/10.1109/TBME.1978.326270

[73] Cohen, S. and Hindmarsh, A.C. (1996) CVODE, A stiff/

nonstiff ode solver in C. In: Holmes, L.M. Ed., Com-

puters in Physics, American Institute of Physics Inc, New

York, 138-143

[74] Hindmarsh, A.C., Brown, P.N., Grant, K.E., Lee, S.L.,

Serban, R., Shumaker, D.E. and Woodward, C.S. (2005)

SUNDIALS: Suite of nonlinear and differential/algebraic

equation solvers. ACM Transacti o ns on Mathematical Soft-

ware, 31, 363-396.

http://dx.doi.org/10.1145/1089014.1089020

[75] Logg, A., Mardal, K.A. and Wells, G. (2012) Automated

solution of differential equations by the finite element

method: The FEniCS book. Springer, New York.

http://dx.doi.org/10.1007/978-3-642-23099-8

[76] Chamberland, E., Fortin, A. and Fortin, M. (2010) Com-

parison of the performance of some finite element discre-

tizations for large deformation elasticity problems. Com-

puters & Structures, 88, 664-673.

http://dx.doi.org/10.1016/j.compstruc.2010.02.007

[77] Haga, J.B., Osnes, H. and Langtangen, H.P. (2012) On

the causes of pressure oscillations in low-permeable and

low-compressible porous media. International Journal for

Numerical and Analytical Methods in Geomechanics, 36,

1507-1522. http://dx.doi.org/10.1002/nag.1062

[78] Hughes, T.J.R. (2000) The finite element method: Linear

static and dynamic finite element analysis. Dover Publi-

cations, Dover.

[79] McIntosh, M.A., Cobbe, S.M. and Smith, G.L. (2000)

Heterogeneous changes in action potential and intracellu-

lar Ca2+ in left ventricular myocyte sub-types from rabbits

with heart failure. Cardiovascular Research, 45, 397-409.

http://dx.doi.org/10.1016/S0008-6363(99)00360-0

[80] Woodworth, R.S. (1902) Maximal contraction, ‘staircase’

contraction, refractory period, and compensatory pause,

of the heart. American Journal of Physiology, 8, 213-249.

[81] Mulieri, L.A., Hasenfuss, G., Leavitt, B., Allen, P.D. and

Alpert, N.R. (1992) Altered myocardial force-frequency

relation in human heart failure. Circulation, 85, 1743-1750.

http://dx.doi.org/10.1161/01.CIR.85.5.1743

[82] Lakatta, E.G. (2004) Beyond Bowditch: The convergence

of cardiac chronotropy and inotropy. Cell Calcium, 35,

629-642. http://dx.doi.org/10.1016/j.ceca.2004.01.017

[83] Boland, J. and Troquet, J. (1980) Intracellular action po-

tential changes induced in both ventricles of the rat by an

acute right ventricular pressure overload. Cardiovascular

Research, 14, 735-740.

http://dx.doi.org/10.1093/cvr/14.12.735

[84] Franz, M.R., Cima, R., Wang, D., Profitt, D. and Kurz, R.

(19920 Electrophysiological effects of myocardial stretch

I. Adeniran et al. / J. Biomedical Science and Engineering 6 (2013) 47-60

OPEN ACCESS

and mechanical determinants of stretch-activated arrhy-

thmias. Circulation, 86, 968-978.

http://dx.doi.org/10.1161/01.CIR.86.3.968

[85] Calkins, H., El-Atassi, R., Kalbfleisch, S., Langberg, J. and

Morady, F. (1992) Effects of an acute increase in atrial

pressure on atrial refractoriness in humans. Pacing and

Clinical Electrophysiology, 15, 1674-1680.

http://dx.doi.org/10.1111/j.1540-8159.1992.tb02954.x

[86] Alvarez, B.V., Pérez, N.G., Ennis, I.L., Camilión de Hur-

tado, M.C. and Cingolani, H.E. (1999) Mechanisms un-

derlying the increase in force and Ca2+ transient that fol-

low stretch of cardiac muscle: A possible explanation of

the Anrep effect. Circulation Research, 85, 716-722.

http://dx.doi.org/10.1161/01.RES.85.8.716

[87] Baartscheer, A., Schumacher, C.A., van Borren M.M.G.J,

Belterman, C.N.W, Coronel, R. and Fiolet, J.W.T. (2003)

Increased Na+/H+-exchange activity is the cause of in-

creased [Na+]i and underlies disturbed calcium handling

in the rabbit pressure and volume overload heart failure

model. Cardiovascular Research, 57, 1015-1024.

http://dx.doi.org/10.1016/S0008-6363(02)00809-X

[88] Calaghan, S.C., Belus, A. and White, E. (2003) Do stretch-

induced changes in intracellular calcium modify the electri-

cal activity of cardiac muscle? Progress in Biophysics and

Molecular Biology, 82, 81-95.

http://dx.doi.org/10.1016/S0079-6107(03)00007-5

[89] Calaghan, S.C. and White, E. (1999) The role of calcium

in the response of cardiac muscle to stretch. Progress in

Biophysics and Molecular Biology, 71, 59-90.

http://dx.doi.org/10.1016/S0079-6107(98)00037-6

[90] Barcenas-Ruiz, L., Beuckelmann, D.J. and Wier, W.G.

(1987) Sodium-calcium exchange in heart: Membrane cur-

rents and changes in [Ca2+]i. Science, 238, 1720-1722.

http://dx.doi.org/10.1126/science.3686010

[91] Hall, J.E. and Guyton, A.C. (2010) Textbook of medical

physiology. 12th Edition, Saunders, Philadelphia.

[92] Rhoades, R. and Bell, D.R. (2013) Medical physiology:

principles for clinical medicine. 4th Edition, Wolters

Kluwer Health/Lippincott Williams & Wilkins, Philadel-

phia.

[93] DiMino, T.L., Ivanov, A., Burke, J.F. and Kowey, P.R.

(2006) Electrocardiography. In: Rosendorff, C., Ed., Es-

sential Cardiology: Principles and Practice, Humana

Press, Clifton, 117-138.

http://dx.doi.org/10.1007/978-1-59259-918-9_8

[94] Klabunde, R.E. (2012) Cardiovascular physiology con-

cepts. 2nd Edition, Lippincott Williams & Wilkins/Wol-

ters Kluwer, Philadelphia.

[95] Bett, G.C. and Sachs, F. (1997) Cardiac mechanosensiti-

vity and stretch-activated ion channels. Trends in Cardio-

vascular Medicine, 7, 4-8.

http://dx.doi.org/10.1016/S1050-1738(96)00119-3

[96] Sengupta, P.P., Tajik, A.J., Chandrasekaran, K. and Khand-

heria, B.K. (2008) Twist mechanics of the left ventricle:

Principles and application. JACC: Cardiovascular Imaging,

1, 366-376. http://dx.doi.org/10.1016/j.jcmg.2008.02.006

[97] Sengupta, P.P., Khandheria, B.K. and Narula, J. (2008)

Twist and untwist mechanics of the left ventricle. Heart

Failure Clinics, 4, 315-324.

http://dx.doi.org/10.1016/j.hfc.2008.03.001

[98] Hodt, A., Stugaard, M., Hisdal, J., Stranden, E., Atar, D. and

Steine, K. (2012) Regional LV deformation in healthy in-

dividuals during isovolumetric contraction and ejection

phases assessed by 2D speckle tracking echocardiography.

Clinical Physiology and Functional Imaging, 32, 372-379.

http://dx.doi.org/10.1111/j.1475-097X.2012.01139.x

[99] Lionel, H.O. (2006) Ventricular Function. In: Rosendorff,

C., Ed., Essential Cardiology: Principles and Practice,

Human Press, New Jersey, 37-54.

[100] Wei, Q., Liu, F., Appleton, B., Xia, L., Liu, N., Wilson,

S., Riley, R., Strugnel, W., Slaughter, R., Denman, R. and

Crozier, S. (2006) Effect of cardiac motion on body sur-

face electrocardiographic potentials: An MRI-based simu-

lation study. Physics in Medicine and Biology, 51, 3405-

3418. http://dx.doi.org/10.1088/0031-9155/51/14/009

[101] Xia, L., Huo, M., Wei, Q., Liu, F. and Crozier, S. (2005)

Analysis of cardiac ventricular wall motion based on a

three-dimensional electromechanical biventricular model.

Physics in Medicine and Biology, 50, 1901-1917.

http://dx.doi.org/10.1088/0031-9155/50/8/018

[102] Smith, N.P., Buist, M.L. and Pullan, A.J. (2003) Altered

T wave dynamics in a contracting cardiac model. Journal

of Cardiovascular Electrophysiology, 14, S203-S209.

http://dx.doi.org/10.1046/j.1540.8167.90312.x

[103] Mao, H.D., Wang, L.W., Wong, C.L., Liu, H.F. and Shi,

P.C. (2011) A coupled heart-torso framework for cardiac

electrocardiographic simulation. Computing in Cardiology,

38, 225-228.

[104] Horner, S.M., Dick, D.J., Murphy, C.F. and Lab, M.J.

(1996) Cycle length dependence of the electrophysiolo-

gical effects of increased load on the myocardium. Cir-

culation, 94, 1131-1136.

http://dx.doi.org/10.1161/01.CIR.94.5.1131

[105] Sung, D., Mills, R.W., Schettler, J., Narayan, S.M., Omens,

J.H. and McCulloch, A.D. (2003) Ventricular filling slows

epicardial conduction and increases action potential dura-

tion in an optical mapping study of the isolated rabbit

heart. Journal of Cardiovascular Electrophysiology, 14,

739-749.

http://dx.doi.org/10.1046/j.1540-8167.2003.03072.x

[106] Kohl, P., Camelliti, P., Burton, F.L. and Smith, G.L. (2005)

Electrical coupling of fibroblasts and myocytes: Relevance

for cardiac propagation. Journal of Electrocardiology, 38,

45-50.

http://dx.doi.org/10.1016/j.jelectrocard.2005.06.096

[107] Thompson, S.A., Copeland, C.R., Reich, D.H. and Tung,

L. (2011) Mechanical coupling between myofibroblasts

and cardiomyocytes slows electric conduction in fibrotic

cell monolayers. Circulation, 123, 2083-2093.

http://dx.doi.org/10.1161/CIRCULATIONAHA.110.0150