Intelligent Control and Automation, 2011, 2, 38-46
doi:10.4236/ica.2011.21005 Published Online February 2011 (http://www.SciRP.org/journal/ica)
Control of Poly-Articular Chain Trajectory Using
Temporal Sequence of Its Joints Displacements
Pierre Legreneur1,2, Thomas Creveaux2, Vincent Bels1
1Departement Ecologie et Gestion de la Biodiversité, Muséum National d'Histoire Naturelle, Paris Cedex, France
2Université de Lyon, Villeurbanne Cedex, France
Received November 9, 2010; revised December 9, 2010; accepted December 20, 2010
Abstract
This paper discusses on the role of joint temporal sequence while moving a two-dimensional arm from an
initial position to targets into the fingertip workspace in humans. For this purpose, we proposed a general
monotonic model of joint asymmetric displacement. Optimization consisted in minimizing least square dis-
placement of either fingertip or arm centre of mass from arm initial position to four targets located into fin-
gertip workspace, i.e. contralaterally and ipsilaterally. Except for 60° ipsilateral target, results of the simula-
tion presented in all cases temporal sequences of the shoulder, the elbow and the wrist. We concluded that
primary function of proximal-to-distal or distal-to-proximal joint sequence is to flatten the trajectory of the
fingertip or body centre of mass.
Keywords: Coordination, Modeling, Simulation, Sigmoid, Pointing, Jumping
1. Introduction
Explosive movements like leaping or jumping are char-
acterized by production of maximal external force at the
interface between the substrate and the body during a
short time. During such movements, most results pre-
sented in the literature exhibits a proximal-to-distal se-
quence of the main engaged limbs, i.e. the most proximal
joint peak velocity occurs before the distal ones. These
coordinations have been reported for various human
movements, e.g. squat jumping [1], sprint push-off [2],
handball throwing [3], football kick while running and
walking [4,5], speed skating [6] o r artistic ice-skating [7].
This sequence of coordination also characterize many
tetrapod taxa using jumping in terrestrial and arboreal
habitats, i.e. bonoboo [8], Galago [9,10], Rana esculenta
[11]. Thus, this sequence appears in various species with
highly different morphologies, occupying different eco-
logical niches and interacting into various tro phic striates.
Consequently, it may reflect mechanical constraints of
the musculo-skeletal systems engaged in animal and hu-
man locomotions [12]. The more the joint approaches its
maximal extension, the less the transformation of the
segment angular velocity into linear velocity is effective
[13]. It is necessary to reduce the velocity of the joint
before its maximal extension (anatomical constraint) in
order to protect this joint from any damage. The proxi-
mal-to-distal sequence allows to delay the negative in-
fluence of the anatomical and geometrical constraints in
explosive movements [14]. This sequence contributes to
produce, transfer and orientate mechanical power, from
proximal to distal segments through mono- and
bi-articular musculo-tendon systems crossing the limb
joints [15-17].
Although proximal-to-distal sequence is well docu-
mented in explosive movements, less information is
available in the literature on poly-articular coordinations
in slow movements, i.e. pointing or grasping tasks [18].
However, by about 24 months of age in humans, proxi-
mal-to-distal sequence emerge in vertical pointing task
between shoulder flexion and elbow extension [19]. Un-
published results obtained in pointing task experiments
conducted in our lab showed that proximal-to-distal se-
quence was mainly chose by subjects whatever the posi-
tion of the target in their arm workspace, i.e. contralat-
eral (75%) vs. ipsilateral (75%) vs. frontal (50%), proxi-
mal (60%) vs. distal (80%). From these results reported
as well in explosive (jumping) as velocity unconstraint
(pointing) movements, we conclude that proximal-to-
distal coordination appears whatever the spatio-temporal
typology of the movement, and could not be only inter-
preted under power transfer mechanisms.

P. LEGRENEUR ET AL.
39
As shown in Figure 1, a common characteristic of all
previously described movements is the linear or quasi-
linear shape of the body centre of mass (CoM) of the
subjects or the distal extremity of the moving poly-arti-
cular chain, e.g. the fingertip in pointing task. Fingertip
trajectory concavity depends also on the spatial position
of the target to reach and increase from ipsilateral to
contralateral sides [20]. In human jumping and animal
leaping, we showed that, whereas the magnitude of the
velocity vector increased all along the CoM trajectory
during push-off, its orientation was reached at 20% of
total push-off time in Microcebus murinus [21] and at
40% in humans [22] and then remained constant. In other
words, after an orien tation phase of the body CoM, these
species tend to maintain their trajectory linear. Trajecto-
ries of fingertip or CoM result from spatio-temporal or-
ganizations of limb segments, i.e. shoulder, elbow and
wrist in pointing task and hip, knee, ankle and meta-
tarso-phalangeal joint in jumping. If we suppose that
these joints move through rotations in a strictly mono-
tonic manner, i.e. exclusive flexion or extension, it is
obvious that simultaneous displacements of joints com-
posing a poly-articular chain will induce angular dis-
placement of its distal extremity or CoM. Thus, we can
predict that linear trajectory of distal end or CoM of a
poly-articular chain results necessary from temporal
joints sequence. The main purpose of the present theo-
retical study was then to test this pred iction.
2. General Model of Joint Displacement
Throughout this paper, we state that the joint angle dis-
placement is a monotonic function of time and that no
regulation of the tr ajectory by the central ner vous system
occurs during the whole joint displacement. Conse-
quently, joint displacement was modelled through a sig-
moid profile (Figure 2(a)) and a velocity bell-shaped
shape (Figure 2(b)) [23,24]. These shapes account for
synergistic actuators activations at a joint, i.e. agonist
and antagonist musculo-tendon systems.
At the start of the movement, the kinematics of the
joint is gi ven by
Figure 1. Stick diagrams of pointing or jumping in human and animals. Arrows indicate the sense of the movements. (a) Arm
pointing task in human to a ipsilateral and distal target. Red circles represent the fingertip; (b) Push-off phase in human
squat jumping. Red circles represent the body centre of mass; (c) and (d) Push-off phase in maximal high leaping in Micro-
cebus murinus and Anolis carolinensis. Red circles represent their body mass centres assimilated to their iliac crest.

P. LEGRENEUR ET AL.
40
time
(
c
)
dis
p
lacemen
t
velocit
y
acceleratio
n
α
β
κ
α
α
(a)
time
(b)
time
Figure 2. Normalized time histories of general joint kinematics. (a) Normalized angular displacement: angle

is achieved
at instant

; (b) Normalized angular velocity: peak velocity

is achieved at instant

; (c) Normalized angular accelera-
tion allowed characterizing a biphasic joint displacement: instant

corresponds to zero acceleration.



0
0
ii
ii
i
t
ttt
t










(1)
Similarly, at the end of the joint rotation,



0
0
ff
f
f
f
t
ttt
t












(2)
Thus, the general formulation of joint displacement is
given by





τ with τ
ii
ff
ifi ifi
tt
tt
tttt t






;
if
ttt














(3)
where

is a function defined on [0, 1] such as
 
0110  . This function is at least of class C²,
i.e. is at least twice continuous and differentiable. More-
over,

has to account for the asymmetric profile of
joint angular velocity reported experimentally [25]. It
should be noted that this asymmetry should be modified
by several constraints. Thus, it increases with spatial
accuracy demands [26]. Moreover, the faster is the
movement, the longer is the acceleration phase [27]. In
other words, the asymmetry of the velocity peak should
be inverted if the velocity exceeds a specific threshold.
Many equations are available in the literature to model
symmetric sigmoid shapes. Fewer equations were de-
veloped for asymmetric shapes, i.e. plant growth [28] or
handwriting [29]. However, they are of class C1 or do not
satisfy equation (3). So, we developed an original sig-
moid model

of class C as:
 

,,
0
1
,,
0
a
a
hydy
hydy



 
 (4)







 
 
  
,,
,
,,
,
,,1
0,0,
0,,1
0,0,
11 0,,1
a
a
a
fygya y
fya y
hyfya y
fyg yay
 



 







 

 




(5)

P. LEGRENEUR ET AL.
41
where

represents the normalized time at which nor-
malized angular peak velocity
 is attained. This in-
stant corresponds to no rmalized joint position

. These
are given by
0i
f
i
tt
tt


 (6)
0i
f
i






 (7)

f
i
fi
K
tt




 (8)
where K repr esents absolute an gular peak velocity. Thu s,
these parameters are linked through the following rela-
tions:



0





 






(9)
,
f


and ,a
g

are given by







,1
1
,
,
00
0,1,
10
n
yy
n
f
yfye
f












 




(10)
And




,
1 0
10,0,
1 0,,1
t
at
a
a
gyea y
ay









 

 


(11)
Solving Equation (9) allows posing
1
1




(12)
From Equations (9) and (11), we can deduce




,
f


:

11
e










 


 (13)
Typical time courses of both joint displacement and
angular velocity are given in Figure 3 for various

values. That illustrates the flexibility of the model for
simulating asymmetric shaped curves on both left
(0.5


) and right (0.5

) sides.
3. Poly-Articular Chain Model
Considering a poly-articular chain composed of a set of p
points
p
A
such as 0
A
is the origin of the reference
frame 0,,
A
ij





R, angular positions of the articulations
are given by
Figure 3. Absolute time histories of general joint displacement for various parameterizations. (a) Angular displacement and
velocity profiles with instant of velocity peak


0.2,0.4,0.6,0.8  . i
t, f
t, i
θ,

f, a and

were fixed at 0, 1, 0, 90, 1
and

respectively; (b) Angular displacement and velocity profiles with beginning of the movement


0.1,0.2,0.3,0.4
i
t.
f
t, i θ,

f,

, a and

were fixed at 1, 0, 90, 0.5, 1 and 0.5 respectively.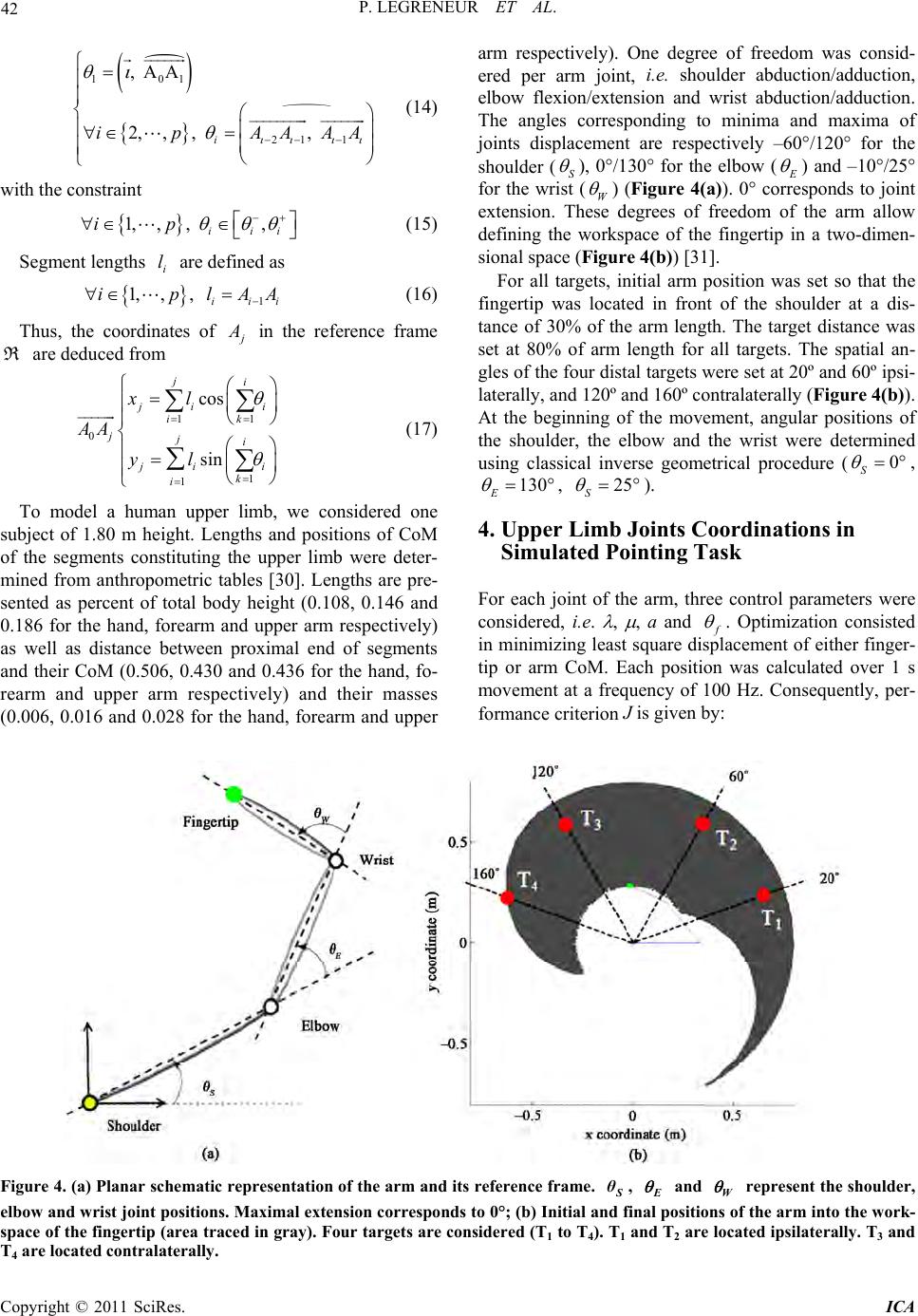

P. LEGRENEUR ET AL.
42




101
21 1
, AA
2,,, ,
i
ipAAAA




 










 


 
 

(14)
with the constraint

1,,, ,
iii
ip





 


 (15)
Segment lengths i
l are defined as

1
1,,, iii iplAA

  (16)
Thus, the coordinates of
j
A
in the reference frame
R are deduced from
11
0
1
1
cos
sin
ji
j
ii
ik
jji
j
ii
k
i
xl
AA
yl








 







 (17)
To model a human upper limb, we considered one
subject of 1.80 m height. Lengths and positions of CoM
of the segments constituting the upper limb were deter-
mined from anthropometric tables [30]. Lengths are pre-
sented as percent of total body height (0.108, 0.146 and
0.186 for the hand, forearm and upper arm respectively)
as well as distance between proximal end of segments
and their CoM (0.506, 0.430 and 0.436 for the hand, fo-
rearm and upper arm respectively) and their masses
(0.006, 0.016 and 0.028 for the hand, forearm and upper
arm respectively). One degree of freedom was consid-
ered per arm joint, i.e. shoulder abduction/adduction,
elbow flexion/extension and wrist abduction/adduction.
The angles corresponding to minima and maxima of
joints displacement are respectively –60°/120° for the
shoulder (S

), 0°/130° for the elbow (
E

) and –10°/25°
for the wrist (W

) (Figure 4(a)). 0° corresponds to joint
extension. These degrees of freedom of the arm allow
defining the workspace of the fingertip in a two-dimen-
sional space (Figure 4 (b)) [31].
For all targets, initial arm position was set so that the
fingertip was located in front of the shoulder at a dis-
tance of 30% of the arm length. The target distance was
set at 80% of arm length for all targets. The spatial an-
gles of the four distal targets were set at 20º and 60º ipsi-
laterally, and 120º and 160º contralaterally (Figure 4(b)).
At the beginning of the movement, angular positions of
the shoulder, the elbow and the wrist were determined
using classical inverse geometrical procedure (0
S


,
130
E


, 25
S


).
4. Upper Limb Joints Coordinations in
Simulated Pointing Task
For each joint of the arm, three control parameters were
considered, i.e.
 ,  , a and
f

. Optimization consisted
in minimizing least square displacement of either finger-
tip or arm CoM. Each position was calculated over 1 s
movement at a frequency of 100 Hz. Consequently, per-
formance criterion J is given by :
Figure 4. (a) Planar schematic representation of the arm and its reference frame.
S
θ,

E
and

W represent the shoulder,
elbow and wrist joint positions. Maximal extension corresponds to 0°; (b) Initial and final positions of the arm into the work-
space of the fingertip (area traced in gray). Four targets are considered (T1 to T4). T1 and T2 are located ipsilaterally. T3 and
T4 are located contralaterally.

P. LEGRENEUR ET AL.
43

101 22
11
2iiii i
Jxxyy



 (18)
The fingertip trajectory was constrained by the mini-
mal distance between its position at the end of the point-
ing task and the target. Moreover, the fingertip final po-
sition was constrained to be at most 5 mm far from the
target. Optimization procedure was performed under
Matlab® 7.3.0 software (Mathworks Inc., Natick, MA,
USA).
Results of the si mulation are p resen ted in Table 1, and
kinematics of the arm is showed in Figure 5 for 20° ip-
silateral target when either fingertip or arm CoM trajec-
tories are optimized. The use of continuous and mono-
tonic functions for joints' displacements induced that the
fingertip is unable to follow a straight line (Figure 5a).
Indeed, the hand path presented a curvature, as usually
observed in the literature [20]. The purpose of the opti-
mization procedure was to flatten fingertip or arm CoM
trajectories. Considering instant of peak velocity  , for
both optimizations (fingertip vs arm CoM) and all targets,
joints moved simultaneously only for 60° ipsilateral tar-
get and arm CoM optimization. In all others cases, tem-
poral sequences are predicted. Regarding to shoulder and
elbow joints, these sequences are either proximal-to-
distal into the ipsilateral space and distal-to-proximal
into the contralateral one. Concerning the wrist, the se-
quence was inconsistent, i.e. the wrist moved before the
elbow or after.
5. Conclusions
The trajectory shape of a point of a poly-articular chain,
or its CoM depends on the temporal organisation of its
constitutive joints displacements. Moreover, we demon-
strated that minimization of path length, or linearization
of this trajectory imposes a temporal sequence of its
joints displacements if these are continuous and mono-
tonic. This sequence is either proximal-to-distal or dis-
tal-to-proximal in function of the location of the ending
position into the work space. In dynamic locomotio n, like
jumping, coordinations are always proximal-to-distal.
That supports the idea that the primary function of
proximal-to-distal sequence in dynamic movement is to
flatten the animal CoM. The secondary function of this
sequence will be to transfer muscle power produce by
mono-articular muscles to the ground through bi-arti-
cular muscles [1] as well as orientate reaction force [16].
Moreover, like model where the magnitude of the jerk
was minimized [24], this theoretical analysis, based only
on the kinematics of the movement, without any optimi-
zation of the musculo-tendon systems activation, is able
to successfully reproduce hand motion.
Table 1. Control parameters values of arm joint angle kinematics for each ending position of the fingertip. For each position,
values are given for digit and arm centre of mass (CoM) trajectory optimizations.
20° 60° 120° 160°
Digit CoM Digit CoM Digit CoM Digit CoM
θf  -25 -22 15 14 74 74 114 114

1.50 0.99 1.32 1.05 1.31 0.60 0.85 0.63

1.50 1.25 0.80 0.96 1.32 1.39 1.41 1.46
a –1.11 –1.02 –1.00 –1.00 –0.20 –1.02 –0.65 –1.06
Shoulder

0.40 0.45 0.56 0.51 0.43 0.42 0.42 0.41
θf  74 78 75 81 81 79 76 78

1.50 1.05 0.72 0.95 1.39 1.47 1.33 1.50

0.64 0.76 0.67 1.04 1.26 0.68 1.15 0.63
a –0.96 –0.98 –1.02 –1.00 –2.31 –0.99 –1.16 –1.01
Elbow

0.60 0.57 0.44 0.49 0.47 0.60 0.52 0.61
θf  7 –10 5 –10 –9 –5 1 –2

1.50 1.00 0.96 1.00 1.50 1.03 1.08 1.09

0.38 0.99 0.95 1.00 1.12 0.95 0.96 0.88
a –0.88 –1.00 –1.00 –1.00 –1.35 –1.00 –1.04 –0.99
Wrist
 0.73 0.50 0.51 0.50 0.47 0.51 0.51 0.53

P. LEGRENEUR ET AL.
44
Figure 5. Predicted kinematics of pointing task for 20° ipsilateral target. (a) and (b) correspond to fingertip and arm centre of
mass (CoM) trajectory optimizations respectively. Stick diagrams of the arm motion are compared with fingertip and CoM
trajectories in case of simultaneous displacements of the joints (thin lines). Below are represented time histories of shoulder,
elbow and wrist angular displacements and velocities.
6. Acknowledgements
This project was conducted under the program ANR06-
BLAN-132-02 and the ATM program of the Museum
National d’Histoire Naturelle (Paris, France) entitled
“Formes possibles, formes réalisées”. We would like to
thank Jérôme Bastien for helping us to model joint dis-
placement.
7. References
[1] L. Gregoire, H. E. Veeger, P. A. Huijing and G. J. van I.
Schenau, “Role of Mono- and Biarticular Muscles in Ex-
plosive Movements,” International Journal of Sports Me-

P. LEGRENEUR ET AL.
45
dicine, Vol. 5, No. 6, 1984, pp. 301-305. doi:10.1055/s-
2008-1025921
[2] R. Jacobs and G. J. van I. Schenau, “Intermuscular Coor-
dination in a Sprint Push-off,” Journal of Biomechanics,
Vol. 25, No. 9, 1992, pp. 953-965. doi:10.1016/0021-92
90(92)90031-U
[3] H. Jöris, A. Muyen, G. J. van I. Schenau and H. Kemper,
“Force, Velocity and Energy Flow during the Overarm
Throw in Female Handball Players,” Journal of Biome-
chanics, Vol. 18, No. 6, 1985, pp. 409-414. doi:10.1016/
0021-9290(85)90275-1
[4] C. Putnam, “A Segment Interaction Analysis of Proximal-
to-Distal Sequential Segment Motion Patterns,” Medicine
and Science in Sports and Exercise, Vol. 23, No. 1, 1991,
pp. 130-144. doi:10.1249/00005768-199101000-00019
[5] J. Van Der Kamp, “A Field Simulation Study of the Ef-
fectiveness of Penalty Kick Strategies in Soccer: Late
Alterations of Kick Direction Increase Errors and Reduce
Accuracy,” Journal of Sports Sciences, Vol. 24, No. 5,
2006, pp. 467-477. doi:10.1080/02640410500190841
[6] G. J. van I. Schenau and K. Bakker, “A Biomechanical
Model of Speed Skating,” Journal of Human Movement
Studies, Vol. 6, 1980, pp. 1-18.
[7] M. Haguenauer, P. Legreneur and K. M. Monteil, “Influ-
ence of Figure Skating Skates on Vertical Jumping Per-
formance,” Journal of Biomecha nics, Vol. 39, No. 4, 2006,
pp. 699-707. doi:10.1016/j.jbiomech.2005.01.005
[8] M. N. Scholz, K. D’Aout, M. F. Bobbert and P. Aerts,
“Vertical Jumping Performance of Bonobo (Pan Paniscus)
Suggests Superior Muscle Properties,” Proceedings of Bi-
ological Sciences, Vol. 273, No. 1598, 2006, pp. 2177-
2184. doi:10.1098/rspb.2006.3568
[9] P. Aerts, “Vertical Jumping in Galago Senegalensis: The
Quest for an Obligate Mechanical Power Amplifer,” Phi-
losophical Transactions of the Royal Society London B,
Vol. 353, 1998, pp. 1607-1620. doi:10.1098/rstb.1998.03
13
[10] M. M. Gunther, “Biomechanische Voraussetzungen beim
Absprung des Senegalgalagos,” Zeitschrift für Morpholo-
gie und Anthropologie, Vol. 75, No. 3, 1985, pp.287-306.
[11] S. Nauwelaerts and P. Aerts, “Propulsive Impulse as a
Covarying Performance Measure in the Comparison of
the Kinematics of Swimming and Jumping in Frogs,”
Journal of Experimental Biology, Vol. 206, No. 23, 2003,
pp. 4341-4351.
[12] G. J. van I. Schenau, “From Rotation to Translation:
Constraints on Multi-joint Movements and the Unique
Action of Bi-articular Muscles,” Human Movement Sci-
ence, Vol. 8, 1989, pp. 301-337. doi:10.1016/0167-9457
(89)90037-7
[13] R. M. Alexander, “Mechanics of Posture and Gait of
Some Large Dinosaurs,” Zoological Journal of the Lin-
nean Society, Vol. 83, 1985, pp. 1-25. doi:10.1111/j.109
6-3642.1985.tb00871.x
[14] M. F. Bobbert and G. J. van I. Schenau, “Coordination in
Vertical Jumping,” Journal of Biomechanics, Vol. 21, No.
3, 1988, pp. 249-262. doi:10.1016/0021-9290(88)90175-3
[15] G. J. van I. Schenau, M. F. Bobbert and R. H. Rozendal,
“The Unique Action of Bi-articular Muscles in Complex
Movements,” Journal of Anatomy, Vol. 155, 1987, pp.
1-5.
[16] R. Jacobs and G. J. van I. Schenau, “Control of an Exter-
nal Force in Leg Extensions in Humans,” Journal of Phy-
siology, Vol. 457, 1992, pp. 611-626.
[17] R. Jacobs, M. F. Bobbert and G. J. van I. Schenau, “Me-
chanical Output from Individual Muscles during Explo-
sive Leg Extensions: The Role of Biarticular Muscles,”
Journal of Biomechanics, Vol. 29, No. 4, 1996, pp. 513-
523. doi:10.1016/0021-9290(95)00067-4
[18] F. Lacquaniti and J. F. Soechting, “Coordination of Arm
and Wrist Motion during a Reaching Task,” Journal of
Neuroscience, Vol. 2, No. 4, 1982, pp. 399-408.
[19] J. Konczak, and J. Dichgans, “The Development toward
Stereotypic Arm Kinematics during Reaching in the First
3 Years of Life,” Experimental Brain Research, Vol. 117,
No. 2, 1997, pp. 346-354. doi:10.1007/s002210050228
[20] Y. W. Tseng and J. P. Scholz, “The Effect of Workspace
on the Use of Motor Abundance,” Motor Control, Vol. 9,
No. 1, 2005, pp. 75-100.
[21] P. Legreneur, F. R. Thévenet, K. M. Monteil, S. J. Mon-
tuelle, E. Pouydebat and V. Bels, “Hindlimb Interarticular
Coordinations in Microcebus Murinus in Maximal Leap-
ing,” Journal of Experimental Biology, Vol. 213, No. 8,
2010, pp. 1320-1327. doi:10.1242/jeb.041079
[22] M. Haguenauer, P. Legreneur, and K. M. Monteil, “Ver-
tical Jumping Reorganization with Aging: A Kinematic
Comparison between Young and Elderly Men,” Journal
of Applied Biomechanics, Vol. 21, No. 3, 2005, pp. 236-
246.
[23] J. F. Soechting and F. Lacquaniti, “Invariant Characteris-
tics of a Pointing Movement in Man,” Journal of Neuro-
science, Vol. 1, No. 7, 1981, pp. 710-720.
[24] T. Flash and N. Hogan, “The Coordination of Arm Move-
ments: An Experimentally Confirmed Mathematical Model,”
Journal of Neuroscience, Vol. 5, No. 7, 1985, pp. 1688-
1703.
[25] H. N. Zelaznik, R. A. Schmidt and S. Gielen, “Kinematic
Properties of Rapid Aimed Hand Movements,” Journal of
Motor Behavior, Vol. 18, No. 4, 1986, pp. 353-372.
[26] T. E. Milner and M. M. Ijaz, “The Effect of Accuracy
Constraints on Three-Dimensional Movement Kinemat-
ics,” Neuroscience, Vol. 35, No. 2, 1990, pp. 365-374.
doi:10.1016/0306-4522(90)90090-Q
[27] R. Plamondon, “A Kinematic Theory of Rapid Human
Movements,” Biological Cybernetics, Vol. 72, No. 4,
1995, pp. 309-320. doi:10.1007/BF00202786
[28] X. Yin, J. Goudriaan, E. A. Lantinga, J. Vos and H. J.
Spiertz, “A Flexible Sigmoid Function of Determinate
Growth,” Annals of Botany (London), Vol. 91, No. 3, 2003,
pp. 361-371. doi:10.1093/aob/mcg029
[29] R. Plamondon and M. Djioua, “A Multi-level Represen-
tation Paradigm for Handwriting Stroke Generation,”
Human Movement Science, Vol. 25, No. 4-5, 2006, pp.
586-607. doi:10.1016/j.humov.2006.07.004

P. LEGRENEUR ET AL.
46
[30] D. A. Winter, “Biomechanics and Motor Control of Hu-
man Movement,” 4th Edition, John Wiley & Sons, Inc.,
Hoboken, 2009. doi:10.1002/9780470549148
[31] J. Bastien, P. Legreneur and K. Monteil, “A Geometrical
Alternative to Jacobian Rank Deficiency Method for Pla-
nar Workspace Characterisation,” Mechanism and Ma-
chine Theory, Vol. 45, No. 2, 2010, pp. 335-348. doi:10.
1016/j.mechmachtheory.2009.09.007