Intelligent Control and Automation, 2011, 2, 31-37
doi:10.4236/ica.2011.21004 Published Online February 2011 (http://www.SciRP.org/journal/ica)
Nonlinear Steam Valve Adaptive Controller Design for the
Power Systems
Nan Jiang, Xiangyong Chen, Ting Liu, Bin Liu, Yuanwei Jing
Faculty of Information Science and Engineering, Northeastern University, Shenyang, China
Received October 21, 2010; revised December 9, 2010; accepted January 10, 2011
Abstract
Considering generator rotor and valve by external disturbances for turbine regulating system, the nonlinear
large disturbance attenuation controller and parameter updating law of turbine speed governor system are
designed using backstepping method. The controller not only considers transmission line parameter uncer-
tainty, and has attenuated the influences of large external disturbances on system output. The nonlinear con-
troller does not have the sensitivity to the influences of external disturbances, but also has strong robustness
for system parameters variation, which is because of the transmission line uncertainty being considered in
internal disturbances. The simulation results show that the control effect of the large disturbance attenuation
controller more advantages by comparing with the control performance of conventional nonlinear robust
controller.
Keywords: Power Systems, Steam Valve Control, Large Disturbance Attenuation, Backstepping, Adaptive
1. Introduction
With the development of large interconnected power
systems and the use of kinds of new equipment, the size
and complexity of power systems is increased, and it is
inevitable that there have the influences of disturbances
on the operation of power system. Meanwhile, owing to
the inaccuracy of the model, the error of the parameters
of the control object designed and the error of the meas-
urement components of the controller also form the gen-
eralized disturbance of power system [1]. In order to
improve the transient stability level of power system, and
prevent an electric power system losing synchronism
under a large sudden fault by closing the turbine regulat-
ing valve quickly to reduce the output of prime mover
instantaneously, it is essential to design the strong ro-
bustness nonlinear steam valve controller to improve its
reliability.
In recently years, various advanced nonlinear control
technologies have been applied to excitation and steam
valve controllers of power systems. Through careful in-
vestigation it is easy to see that most of these are based
on some different control methods. However, these con-
trollers suffer some flaws. Robust adaptive controller and
nonlinear stabilizing controller of steam valve and exci-
tation system design method are presented based on
Hamiltonian energy theory in [2,3], but it is difficult to
solve the Hamilton-Jacobi-Issacs (HJI) inequality. In
order to avoid solving the HJI inequality, Lu [1] de-
signed the nonlinear L2 gain disturbance attenuation ex-
citation controller based on recursive design method for
the external disturbance attenuation problem. Li [4] de-
veloped a multivariable inverse nonlinear control scheme
for strongly nonlinear reheat type turbo generator steam
valves, which provides whole range control to improve
the transient power system stability. In [5-7], the turbine
governor and excitation controller design method using
no linearization methods when system parameters are
precisely knowable are proposed, but the robustness of
the parameters and model was not considered. For a sin-
gle-machine infinite -bus system, Wang [8] designed a
nonlinear robust integrated controller and a parame-
ter-update law is obtained based on adaptive backstep-
ping methods and Lyapunov functions of the system. The
controller also has strong robustness for system parame-
ters variation because damping coefficient uncertainty
has been considered. In order to prevent an electric
power system losing synchronism under a large sudden
fault and to achieve voltage regulation, Wang [9] applied
the Riccati equation approach, together with the direct
feedback linearization (DFL) technique to design robust
nonlinear controllers for transient stability enhancement

N. JIANG ET AL.
32
and voltage regulation of power systems under a sym-
metrical three-phase short circuit fault. Sun [10] de-
signed the nonlinear adaptive controllers and parameter
updating laws of the switch subsystems using the pro-
posed modified adaptive backstepping method for a sin-
gle- machine-infinite-bus system, the control input con-
straints are solved by introducing a switched mechanism.
In [11-13], the nonlinear adaptive controllers and pa-
rameter updating laws for a single-machine-infinite- bus
system with damping coefficient uncertainties in the tur-
bine steam valve control also are proposed. However, the
influences of the external unknown disturbances are not
considered. Thus, how to effectively deal with the influ-
ences of the external unknown disturbances on system
output for the origin system is valuable to be further
studied.
Thus, in this paper we use the backstepping method to
design the nonlinear disturbance attenuation controller
and parameter updating law of turbine speed governor
system for the uncertainty of transmission line parame-
ters and the influences of large external disturbances on
system output. In the design process, the influences of
disturbances are considered while it does not use any
linearization methods. Thus, the nonlinear controller
does not have the sensitivity to the influences of external
disturbances, but also keep the nonlinearities of systems.
The simulation result demonstrates that the disturbance
attenuation controller possesses superior performances
by comparing with the control performance of conven-
tional nonlinear robust controller. The design procedure
based on the adaptive backstepping method is systematic
and concise, it is believed that this method can be ac-
cepted with a considerable ease by engineers.
2. Model and Problem Statement
Consider the following single-machine infinite-bus sys-
tem with steam valve control and the configuration of
whole system is shown in Figure 1.
Then the model of main steam-valve control system is
expressed as follows [11]:
Δδ, Δω, ΔP
m
Figure 1. A single-machine infinite-bus system with the
steam valve control.


0
0
0e
0
1
HMLm D
HHHmH
H
PCP PP
H
PPCPCu
T










 





(1)
where

is the rotor angle of generator.

is the rotor
speed of generator. m P, e P,
D
P,
H
P are mechanical
power of prime motor, active power of generator, damp-
ing power and mechanical power generated by high-
pressure cylinder, respectively. H is the inertial coeffi-
cient of generator.
H
T

is the equivalent time constant
of valve control, the value is about 0.4.
H
C is the dis-
tribution coefficient of high-pressure turbine, it is about
0.3.
M
L
C is the distribution coefficient of middle and
low-pressure turbine power, it is about 0.7. 0m P is the
initial value of mechanical power, 00me PP. u is the
steam-valve control. And we know that:

'
0
'
0
sin,
qS
eD
d
EV D
PP
X





(2)
where D and '
q
E are damping coefficient and transient
EMF of generator q axis, respectively. S V is the infinite
bus voltage. '
d
X

is the equivalent reactance between
generator and infinite bus system.
Next, we will research the design of the controller
when the parameter '
d
X

is unknown. For system (1), in
order to transform it into the appropriate form in back-
stepping design, let 10 x



, 20 x

  and
30mm
x
PP

, where 0

, 0

, 0m P are the initial value
of corresponding variables, then system (1) can be re-
written as follows:


12
0
22300
3300
1
mMLme
mHmH
H
xx
D
x
xxPCPP
HH
xxPCPCu
T





 


 





(3)
Let 1
D
k
H

, 0
2
k
H

, 1
H
TT  ,
0 a


0
00mMLm
PCP
H

,
H
H
C
CT

 ,
and they are known constants. Further, let
'
0
'
qS
d
EV
HX




and they are unknown parameter because of '
d
X

. Fi-
nally, consider the exogenous disturbance

12
T

 ,
where 1

and 2

is the disturbance on generator rotor
and steam valve, respectively. Then system (3) is trans-

N. JIANG ET AL.
33
formed into:
12
x
x
 (4)

212 2302011
sinxkxkxa kx

  
 (5)

3302
xTxb Cu


 (6)
11
22
qx
Zqx



(7)
where

112 2
T
Z
qx qx is regulation output; 1 q and
2
q are the non-negative weight coefficient, which rep-
resent the weighted proportions between 1
x
and 2
x
.
Now we can note that the system (7) is a control sys-
tem with parametric uncertainties and unknown control
gain, as well as unknown bounded exogenous distur-
bances. Our control objective is to keep the rotor stable
and the system states are stabilized simultaneously.
3. Design of Nonlinear Adaptive Controller
with Large Disturbance Attenuation
For the controlled object with the uncertain parameters
and external disturbances, we can use the adaptive back-
stepping method to design the nonlinear robust controller
of steam valve. We can design a suitable controller u
by constructing the storage function

Vx, and then the
system satisfies:
   

22
2
0
0T VxtVxz dt   

where any 0T, the 2
L gain of system less than

,
and

is the disturbance attenuation constant.
Noticing the above-mentioned facts, the analysis
method and design process of controller can be summa-
rized as follows:
Step 1: For subsystem (4), let 2
x
as the virtual con-
trol, and take stabilizing function *
211
x
cx, 10c is
a design constant; suppose 11 ex, *
222
exx, then
subsystem (4) can be expressed as
1211
eecx

Via taking the first Lyapunov function candidate as
2
11
2
Ve

 (8)
where 0

, then the time derivative of 1 V found is

2
1111211 1211
Veeeece eece    
 (9)
Step 2: By augmenting (9), the new Lyapunov func-
tion can be formed as
2
21 2
1
=+
2
VV e (10)
Suppose that
22
2
12 1
1
2
HV Z



 


 (11)
and the performance index can be supposed as follows,


22
2
11
0
J
Zdt 



then one gets



22 2222
121112 1
2
12 11
21223020 11
2
2222 2
21 21 122111
1
2
sin
11 1
22 2
H Vqxqx
ee ce
ekxkxakx
ecxqeq ece







 



  


 

(12)
By deviating (12) about 1

and supposing the first
derivation is equal to 0, we can get
2
21
0e 


then (13) can be obtained as follows,
*
12
2
1e
  (13)
We continue to find the second derivation of (12), one
gets
22
1
2
1
0
2
H 

 

Then there is the maximum value of 1
H
about 1

.
22
2
12 1
1
max max2 HVZ 








 (14)
Now get the integral both sides of (14), we can get

1
0
22
2
21
00
max
1
max 2
Hdt
Vdt Zdt













Let 11
0
H
Hdt

, then
 

1
122
maxmax0 2
J
HVV







Owing to 1
12
2
J
H
V

 , one gets



1
12
12
max max
2
max min
J
H
V
HV





Remark 1: Suppose that the disturbance 1

makes
2
V reduce to 0, i.e.


2
min 0V, that is, when the

N. JIANG ET AL.
34
systems have the sufficiently large disturbances, 2 V is
not reduced, and then,


1
max 2J is equivalent to

1
max
H
, so 1

is really the worst disturbances for
system.
Remark 2: Based on the equivalent analysis of

1
max
H
and

1
max 2J, 1

make 1
H
get the
maximum value means that 1

makes 1
J
also obtain
maximum. While our ultimate goal is to make 1
J
minimum, then explain 1

on the system's performance
damage is the largest. If we substitute disturbances with
such damage degree into systems, based on which we
design the controller, and ensure the stability of the
closed-loop system. Thus it shows that the system is not
sensitivity for the influences of disturbances in theory.
Substituting (13) into (12), there is

2
11211
212230 201
22 22 22
2122 1122
2222
2211211
sin
111
222
1
2
Heece
ekxkxakx
ecxe qe qe
qece qce





 

  

Suppose that
222
1112 1
2
1211
2
2
2121
2
11
,
22
11
,
22
11
2 2
cq qc
hqcc
hcqk




 

Then


2
1121122230201
sin
H
eehxhxkxa kx 

 

Consider 3
x
as the virtual control, and define that
*
333
exx, then choosing the new virtual stabilization
function as follows,

*
31122020122
2
1sin
x
hxh xakxce
k
   

Let

12 01
sinnk x   , where 2 c is a positive num-
ber to be selected.
*
311220122
2
1
x
hxh xance
k

  

We can obtain

22
11222201
sin
H
eceek x   

where

 
,

is the estimated value of

.
Step 3: By augmenting 2 V, the new Lyapunov func-
tion can be formed as
22
32 3
11
22
VV e


 (15)
where 0

 is the adaptive gain coefficient.
Define that
22
2
23
1
2
HV Z







and the performance index as follows,


22
2
20
J
Zdt 



Because 3233
1
VVee



  

 , and
 
  
 
*
31122212122
2
112212 230
2
2022 12122
2
1
1
1
sin
xhxhcxnnccx
k
hxhckxk xa
k
kkennccx

 






 











one gets


 


22 22222
2 23311 221 2
22 22
12222 012
330231222
2
12 23 02012
2
12
11 1
22
11
sin2
1
1
sin
HVeeqxqx
eceekx
eTx bcuehxhc
k
kxkxakxe
nnc








 

 
 
 


 


 

 




 12 2
cx
(15)
By deviating (15) about 2

and supposing the first
derivation is equal to 0, we can get
*
23
2
1e
  (16)
To find the second derivation of (15), we can obtain
22
2
2
2
0
2
H





,
So there is the maximum value of 2
H
about 2

.
Then, we know that *
2

is the most disturbance of sys-
tem to make a performance cost 2
J
be the largest
value.
Substituting (16) into (15), then


22
21222201
33 303
22
sin
11 1
2
Heceek x
eeTxbcue



 

 






N. JIANG ET AL.
35
  


3
12221223 0
2
2
201 12122
2
sin
ehxhckxk xa
k
e
kx nnccx  

 









Choosing the feedback control as follows,
 


3
3012 22
2
2
2
12 23 011
2
212233
11 e
uTxb hxhc
ck
e
kxkxann
nccxce





  







 

then,


22
21222201
2
2 33
332 21
2
2
1
sin
2
Heceek x
ee
ceh cn
k

 



 




In order to ensure that 20H

, suppose that
  
220 132 20 1
1
sinsin 0ekxehcx  

 


 
2132 201
1sin 0enehcx
 


 




Choosing the parameter update law
 
2132 201
sinene hcx  
  


By choosing the appropriate coefficient

, so 0

,
then
222
212233
0Hecece  
Let
 
3
2VxV x, one gets

22
2
Vx z  
 (17)
where

12
T

 . When


00x, we get the inte-
gral both sides to satisfy the inequality (17), so there are
the gain from disturbance to output.
Remark 3: when the system operates normally, then
0 180  

, and we can know that

01
sin
x
 0

,
so the control is defined.
Now get the integral both sides of (17), the dissipation
inequality can be obtained as follows,
   

22
2
0
0T VxtVxz dt   

so there is L2 gain from disturbance to the output of sys-
tem. And when 0

, the closed-loop error control sys-
tem is asymptotic stable with the feedback control law u,
then the closed-loop control system can be expressed as
follows,


1211
1
2221
2
2
1121
3332
2
1123
2
1
2
22
eece
n
ecee
k
ckcn
ece k
ckce
en
kk






 









 












 
(18)
4. Simulation Examples
In this section, we firstly analyze the stability of the sys-
tem by analyzing the state responses of system, which is
generated by Simulink. Further, when the system pa-
rameters change under the fault that occurs, we observe
the stability time of system with the influence of nonlin-
ear steam valve adaptive robust controller, so we can
analyze the stability of nonlinear steam valve adaptive
robust controller of power system based on adaptive
backstepping method, and the bounded ness of the state
of system and whether to suppress the influences of large
external disturbances on system output also can be ana-
lyzed.
4.1. Simulation of General Nonlinear Robust
Controller
In this subsection, we can give the simulation analysis of
general nonlinear robust controller, and the transient re-
sponding curves of the system output state and the con-
troller output can be shown in Figure 2 and Figure 3.
The general nonlinear robust steam valve controller
can be designed using the general backstepping method.
As this robust controller, the time of the stability of sys-
tem is longer and it will keep a slow convergence.
Moreover, it will maintain the small oscillation stability
within a certain range, and the control is ineffective.
x
1
Figure 2. The transient responding curves of the system
state x1.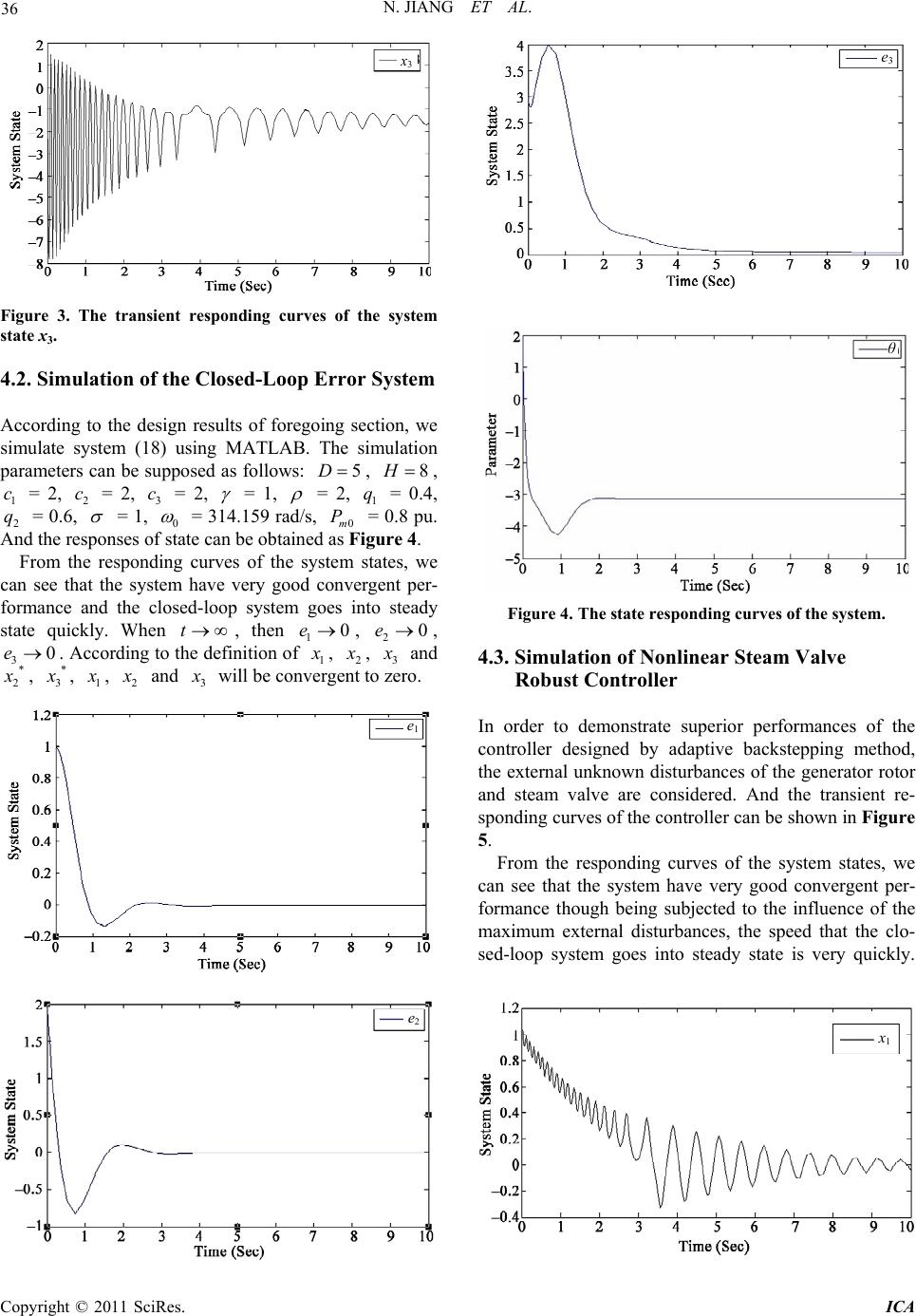

N. JIANG ET AL.
36
x
3
Figure 3. The transient responding curves of the system
state x3.
4.2. Simulation of the Closed-Loop Error System
According to the design results of foregoing section, we
simulate system (18) using MATLAB. The simulation
parameters can be supposed as follows: 5D, 8H

,
1
c = 2, 2 c = 2, 3 c = 2,

= 1,

= 2, 1 q = 0.4,
2
q = 0.6,

= 1, 0

= 314.159 rad/s, 0m P = 0.8 pu.
And the responses of state can be obtained as Figure 4.
From the responding curves of the system states, we
can see that the system have very good convergent per-
formance and the closed-loop system goes into steady
state quickly. When t , then 10e, 20e,
30e. According to the definition of 1
x
, 2
x
, 3
x
and
*
2
x
, *
3
x
, 1
x
, 2
x
and 3
x
will be convergent to zero.
e
1
e
2
e
3
θ
Figure 4. The state responding curves of the system.
4.3. Simulation of Nonlinear Steam Valve
Robust Controller
In order to demonstrate superior performances of the
controller designed by adaptive backstepping method,
the external unknown disturbances of the generator rotor
and steam valve are considered. And the transient re-
sponding curves of the controller can be shown in Figure
5.
From the responding curves of the system states, we
can see that the system have very good convergent per-
formance though being subjected to the influence of the
maximum external disturbances, the speed that the clo-
sed-loop system goes into steady state is very quickly.
x
1

N. JIANG ET AL.
37
x
3
Figure 5. The response curve of the system state.
Thus all of these do verify the design process in this pa-
per.
5. Conclusion
In this paper, we apply the nonlinear adaptive robust
control scheme to turbine speed governor system. Non-
linear adaptive robust controller of steam-valve with the
large external disturbances attenuation technique is de-
signed by combining adaptive backstepping method. The
essential nonlinear nature of the systems is entirely pre-
served because of no use of any kind of linearization on
the original nonlinear system model. Owing to the fact
that both internal and external disturbances in controller
design are considered together, we compared the de-
signed controller with the more conventional, not only
the designed nonlinear controller does not have the sen-
sitivity to the influences of external disturbances, but
also has strong robustness for system parameters varia-
tion. The further simulations demonstrated the controller
has superior adaptability and robustness.
6. Acknowledgements
This work is supported by the Fundamental Research
Funds for the Central Universities, under grant 090304004,
and the National Natural Science Foundation of China,
under grant 60274009, and Specialized Research Fund
for the Doctoral Program of Higher Education, under
grant 20020145007.
7. References
[1] Q. Lu, S. W. Mei, T. L. Shen, et al., “Recursive Design
of Nonlinear H∞ Excitation Controller,” Science in China
(SeriesE), Vol. 30, No. 1, 2000, pp. 70-78.
[2] S. J. Li, Z. Yu and G. Wang, “Adaptive H-Infinity Con-
trol of Synchronous Generators with Steam Valve via
Hamiltonian Function Method,” Journal of Control The-
ory and Applications, Vol. 4, No. 2, 2006, pp. 105-110.
doi:10.1007/s11768-006-5059-6
[3] J. Ma, Z. R. Xi, S. W. Mei, et al., “Nonlinear Stabilizing
Controller Design for the Steam-Valuing and Excitation
System Based on Hamiltonian Energy Theory,” Pro-
ceedings of the CSEE, Vol. 22, No. 5, 2002, pp. 88-93.
[4] H. R. Ri, D. H. Li and L. Q. Li, “Reheat-Type Turbo
Generator Steam Valve Whole-Range Non-linear Con-
trol,” Journal of Tsinghua University (Science and Tech-
nology), Vol. 40, No. 10, 2000, pp. 89-92.
[5] Y. Z. Sun, Q. Lu and C. X. Sun, “On the Study of Power
System Nonlinear Robust Control,” Proceedings of the
CSEE, Vol. 16, No. 6, 1996, pp. 361-365.
[6] Y. Z. Sun, X. Li and H. P. Dai, “Nonlinear Excitation
Controller to Improve both Power System Stability &
Voltage Regulation Accuracy,” Proceedings of the CSEE,
Vol. 16, No. 5, 1996, pp. 332-335.
[7] Q. Lu and Y. Z. Sun, “Nonlinear Control of Power Sys-
tems,” Science Press, Beijing, 1993.
[8] B. H. Wang, C. W. Yang, Q. Zhang, et al., “Integrated
Nonlinear Adaptive Backstepping Controller for Synchro-
nous Generator,” Control Theory & Applications, Vol. 23,
No. 1, 2006, pp. 60-64.
[9] Y. Y. Wang and J. David, “Robust Nonlinear Coordi-
nated Control of Power Systems,” Automatica, Vol. 32,
No. 4, 1996, pp. 611-618. doi:10.1016/0005-1098(95)00
186-7
[10] Li. Y. Sun and J. Zhao, “Nonlinear Adaptive Control for
the Turbine Steam Valve with Input Constraints,” Con-
trol Theory & Applications, Vol. 6, No. 6, 2009, pp.
601-606.
[11] W. L. Li, Y. W. Jing and M. S. Wang, “Stability Control
in Power Systems: A Survey,” Control and Decision, Vol.
17, No. 6, 2002, pp. 1-6.
[12] W. L. Li, Y. W. Jing and X. P. Liu, “Adaptive Robust
Backstepping Design for Nonlinear Steam Valve Con-
troller,” Proceedings of the CSEE, Vol. 23, No. 1, 2003,
pp. 155-158.
[13] W. L. Li, “Study on the Nonlinear Adaptive Robust Con-
trol for Power Systems,” Ph.D. Thesis, Northeastern
University, Shenyang, 2003.