Paper Menu >>
Journal Menu >>
 Intelligent Control and Automation, 2011, 2, 1-7 doi:10.4236/ica.2011.21001 Published Online February 2011 (http://www.SciRP.org/journal/ica) Copyright © 2011 SciRes. ICA Distributed H Consensus of High-Order Multi-Agents with Nonlinear Dynamics* Jianzhen Li School of Automation, Nanjing University of S cience and Technology, Nanjing, China E-mail: jianzhenli1983@yahoo.com.cn Received January 20, 2011; revised February 12, 2011; accept ed Fe bruary 13, 2011 Abstract This paper deals with the distributed consensus problem of high-order multi-agent systems with nonlinear dynamics subject to external disturbances. The network topology is assumed to be a fixed undirected graph. Some sufficient conditions are derived, under which the consensus can be achieved with a prescribed H norm bound. It is shown that the parameter matrix in the consensus algorithm can be designed by solving two linear matrix inequalities (LMIs). In particular, if the nonzero eigenvalues of the laplacian matrix ac- cording to the network topology are identical, the parameter matrix in the consensus algorithm can be de- signed by solving one LMI. A numerical example is given to illustrate the proposed results. Keywords: Consensus, Multi-Agent Systems, Nonlinear Dynamics, External Disturbances 1. Introduction The consensus problem of multi-agent systems has been researched extensively in recent years. This is because of its widely application in much areas such as flocking [1-2], synchronization of coupled oscillators [3], forma- tion control of mobile robots [4-5], distributed computa- tion [6] and information fusion in wireless sensor net- works [7]. The object of consensus control is to design consensus protocol such that the group of agents can asymptotically agree upon certain quantities of interest based on information received from their neighbors. Most of the work on the consensus problem focuses on the multi-agent systems with first-order dynamics. In particular, [8] deals with the first-order multi-agent sys- tems with switching topolog ies and time delays in a con- tinuous setting. The fist-order multi-agent systems with switching topologies is investigated in [9] in a dis- crete-time setting. The consensus problem has also been investigated from many other aspects such as reference signals [10], asynchronous sampling time [11], and so on. Recently, the consensus problem of second-order multi- agent systems has been investigated extensively [12-14]. In particular, the consensus problem of second-order multi-agent systems with nonlinear dynamics was inves- tigated in [15]. The nonlinear dynamics can be taken as the potential functions or the desired final dynamics of the agents. There is also some work on the consensus problems of high-order multi- agent systems [16-17]. Generally speaking, the consensus cannot be achieved accurately if there are external disturbances. To deal with this problem, the H consensus problem is considered [18-21]. It is shown that for undirected network topolo- gies, the desired parameter matrix in the con sensus algo- rithm can be designed by solving two LMIs, which relate to the system matrix of the ag ents and the eigenvalue s of the laplacian matrix corresponding to the network topol- ogy. The 2 H consensus problem was investigated in [22]. In the aforementioned work on the H or 2 H con- sensus problem, the nonlinear dynamics was not consid- ered. As is mentioned in [14-15] much multi-agent sys- tems have nonlinear dynamics. Motivated by this, this paper considers the H consensus problem of high- order multi-agent systems with nonlinear dynamics. To the best of the author's knowledge, this problem has not been considered in the literature. Some sufficient condi- tions will be derived, under which the consensus can be achieved with a prescribed H norm bound. It will be shown that the parameter matrix in the consensus algo- rithm can be designed by solving two LMIs, which relate to the system matrix of the agents and the smallest and *This work was supported by the National Natural Scie nce Fou nda tio n of P. R. China under Grant 60904022.  J. Z. LI Copyright © 2011 SciRes. ICA 2 the biggest nonzero eigenvalue of the laplacian matrix corresponding to the network topology. In particular, if the nonzero eigenvalues of the laplacian matrix accord- ing to the network topology are identical, the parameter matrix in the consensus algorithm can be designed by solving one LMI. 2. Preliminary Notations and Problem Formulation Let ,, be a weighted undirected graph of order N, where 1,, N is the node set. is a set of unordered pairs of nodes, and is the adjacency matrix. An undirected path is a se- quence of edges in a undirected graph of the form 12 v,v , ii 23 v,v , ii, where 12 , ii vv An undi- rected graph is called connected if for any two nodes of the graph, there ex ists a p ath that fo llows the edge s of the graph. The adjacency matrix is a nonnegative matrix N N dij a satisfying a0 ii for any i , aa0 ij ji , if ,ji , and a0 ij if agents j and i are not adjacent. The Laplacian matrix of the graph is defined as N N ij l with ii ij ji la and la, . ijij ij We can see that satisfies 01 and 0 T1 where .1,,1T 1 For matri- ces M and N, M N denotes their Kronecker product. It is well known that if the undirected network topology is connected, the lapalacian matrix corresponding to has 1N positive eigenvalues and a simple zero eigenvalue. Consider a group of N agents with the following dy- namics: 12, iii ii x AxBuBB fx (1) where , m i xt p i ut are, respectively, the state, the control input of agent i, m it is the external disturbance which belongs to 20, , and m i fx is a nonlinear function. Assumption 1: There exists a positive scalar such that , ,. T ij ij T ij ij m ij f xfx fxfx xx xx xx Remark 1: Assumption 1 is similar to the Assumption 1 in [14]. It is a Lipschitz-type condition satisfied by many systems. Definition 1: We say algorithm ui solves the con- sensus problem if 10, , . Nj ij x xti N Definition 2: We say algorithm ui solves the con- sensus problem with H norm bound if the fol- lowing two conditions are satisfied: 1) Algorithm ui solves the consensus problem if 0; 2) If 00,z the following inequality is satisfied: 22 2 00 ,zdt dt where 1 1 1 , , , Nj ii j T TT N T TT N x zx N zz z and 0 z is the initial value of z. The object of the H consensus control is to design consensus algorithms such that the consensus problem is solved for a presc ribed H norm bound. Lemma 1: (Schur complement [23]) Let S be a sym- metric matrix of partitioned form ij SS with 11 , rr S () 12 rnr S and ()() 22 nr nr S Then, 0S if and only if 11 0,S 1 2221 11120,SSSS or equivalently 1 221112 2221 0, 0. SSSSS Lemma 2: For matrices A, B, C, D with appropriate dimensi ons, o n e has , TTT A BABCDACBD and A BCACBC 3. Results In this section, the H consensus problem of multi- agent systems with nonlinear dynamics will be investi- gated. Considers the following state feedback consensus algorithm: 1 N iijij j utKa xx (2) With (2), system (1) becomes 12 1, N iiijijii j x AxBKaxxBBfx (3) which can be written in a compact form as 1 2 , NN N xI ALBKxIB IBf (4) where 1 , N TT T xx x and 1 () (). T TN T ffx fx By the definition of z we have the consensus is achieved if and only if 0z as .t It is easy to see that  J. Z. LI Copyright © 2011 SciRes. ICA 3 , m zHIx (5) where N N H with 1, 1,. ij Nij N H ij N It can be seen that , T N H IN11 2, H H , TT N N H10 N N H10 and .HH Lemma 3: There exists an orthogonal matrix N N U with last column NN1H such that 11 1 ,. *0 *0 Nn N TT I UHU ULU 00 From (4) and (5) we have 1 2 1 2 . m zHIx HALBKxHB HBf HALBKzHB HBf (6) Define 1N UU N 1 , from Lemma 3 we have 111 TN UHU I and 11. T ULU Define Tm UIz 1, T TT N we have 12 11 1 11 12 11 *0 *0 . Tmm TT mm Nn N TT TT NN UIHALBKUIz UI HBUI HBf IABK UH UH BBf 00 00 (7) It can be seen that 0 N . So 0 if and only if 0 i , 1, ,1.iNDefine 11 . T TT N From (7) we have 1 11 12 . N TT IA BK UHBUHB f (8) Note that the eigenvalues of are 2,,. N There exists an orthogonal matrix 11NN F so that 2,, . TN FF diag Define 11 T TTT mN FI we have 12 11 12 ,, . NN TT TT IAdiag BK F UHBFUHB f (9) Noting that , TT TT zz we conclude that algorithm (2) solves the consensus problem with H norm bound if and only if system (9) is asymp- totically stable with ,T where T denotes the H norm of the transfer function matrix from to . Theorem 1: Suppose the undirected graph is connected and the nonzero eigenvalues of are 2,, N . Using algorithm (2), the consensus is achieved with H norm bound if there exists a symmetric positive definite matrix X and a matrix W such that the LMIs 12 2 1 2 000, 00 1 00 1 T Tm m m BXBX BI BI XI (10) 2, ,iN hold, where . TTT i A XXA BWWB In this case, the parameter matrix in (2) can be chosen as 1. K WX Proof: Assume that the undirected graph is con- nected, we have 20 . Suppose there exists a symmet- ric positive definite matrix X and a matrix W such that (10) hold. Define 1,WPX 1. K WX Pre- and post-multiply both sides of (10) by 000 000 00 0 000 m m m P I I I one can get 12 2 1 2 000, 00 1 00 1 Tm Tm m mm PB BI BP I BI II (11) 2, , iN hold, where TTT i P AAP PBKKBP . For , i 3, ,1,iN there exists 01 i such that 21. iN It is easy to see that (11) also holds for 3, ,1iN . By Lemma 1 we know that (11 ) holds if and only if 22 1 2 1 10 Tm Tm BBI PB BP I (12) holds. Define  J. Z. LI Copyright © 2011 SciRes. ICA 4 11 2 11 1 , N T NNm IPB IPB I where 2 1 122 1 ,, . TT N Nm TT NN m I diagPBKKB P IBBIPAAPI From (12) we know that 0. Next prove that the consensus is achieved if 0. If 0 , (9) becomes 12 12 ,, . NN TT IA diagBK FUHB f (13) Consider the Lyapunov function 1. TN VIP Because P symmetric positive definite, we have V is symmetric positive definite with respect to . Taking derivative of V along (13), we have 11 12 112 1 2 12 2 2,, 2 ,, 2. TNN TNN TTT N TT N TT N TTT VIPIA IPdiagBK IPFUHBf IPAAP diagPBKKB P FUHB f (14) Because U is an orthogonal matrix, one has 11 T TNN N IUUU U NN 11 It follows that 111 . TN UU I Then we have 12 11 22 2 122 2 . TTT TTT T Tm TTT Nm FUHB f FUUF BB fH If I BBf H I f (15) Notice that 1 1 1 1 Tm NT ij ij iji NT ij ij iji fHIf f xfx fxfx N xx xx N . Tm TT x HIx zz (16) From (14)-(16) we have 1 2 122 122 2 ,, ,,. TT N TT N TT T N TTT Nm TT N V IPAAP diagPBKKB P IBB IPAAPBBI diagPBKKB P (17) It follows from (12) that 22 0,1 Tm BB I which, together with (17) implies th at V is negative definite with respect to . It then follows that 0 asymptotically. From the analysis above we know the consensus can be achieved. Assume that 0. Taking derivative of V along (9), we have 11 211 12 122 2 11 2 ,, ,, 2. TNN TT N TT TTT Nm TT N TTT VIPIA diagBKF UHB FUHB f IPAAPBB I diagPBKKB P FUH PB (18) Assume that 00z , which implies that 00 , where 0 is the initial state of . It follows that 22 2 00 22 20 0 2 0 122 2 11 0 ,, 2 , TT TTT Nm TT N TTT T zdt dt VdtV V IPAAPBBI diagPBKKB P FUH PBdt dt (19) where , T TT 00V is the initial value of V , and 11 2 11 . TT T Nm FUH PB HU FPBI  J. Z. LI Copyright © 2011 SciRes. ICA 5 By Lemma 1 we know that 0 if and only if 2 1111 2 2 111 2 ,, 1() ,, 1 0. TT N T TT TT N T N diagPBKKB P FUHPBHUF PB diagPBKKB P IPBBP (20) Also by Lemma 1 we know that (20) is equivalent to 0 , which has been proved in the above analysis. So we have that is symmetric negative definite. It fol- lows from (19) that 22 2 00 0.zdt dt Therefore, the consensus is achieved with H norm bound . The proof is completed. Sometimes, the laplacian matrix has 1N identical nonzero eigenvalues, i. e. 2 0 N . Take the complete graph for example. Consider the complete graph wit h N nodes. The laplacian matrix is chosen as 111 11 1 . 11 1 N NN N N NN N N NN N By some calculations we have the eigenvalues of are 11 0,, , 11NN . In this case, we have the fol lowing corollary. Corollary 1: Suppose the undirected graph is connected and the nonzero eigenvalues of satisfy 2. N Using algorithm (2), the consensus is achieved with H norm bound if there exists a symmetric positive definite matrix X and a matrix W such that the LMI 12 2 1 1 2 000, 00 1 00 1 T Tm m m BXB X BI BI XI (21) holds, where 1. TTT A XXA BMMB In this case, the parameter matrix in (2) can be chosen as 1. K WX Proof: Assume that there exists a symmetric positive definite matrix X and a matrix W such that (21) holds. Define 2 1.X M W It follows that 12 2 1 2 000 00 1 00 1 T Tm m m BXBX BI BI XI Holds for 2.i From Theorem 1 we have the con- sensus is achieved with H norm bound , and the parameter matrix can be chosen as 1. K WX Remark 2: From Corollary 1 one has that if the non- zero eigenvalues of the laplacian matrix are identical, the H performance is determined by 2 and the system matrices of the agents. It has no relationship with the number of the agents. 4. A Numerical Example Consider a multi-agent systems consisted of N nodes with the following second-order , sin0.5, iiiiii i x vvu x where 1 sin 1 it is the external disturbance. This multi-agent system can be written in the form of (1) with 12 01 01000 , , , . 00 10101 ABB B The communication topology is given in Figure 1. The laplacian matrix is chosen as 1100 12 10 . 0121 001 1 The eigenvalues of are 0, 0.5858, 2 and 3.4142. Solving the LMIs in (10) with 20.5858 , 4 3.4142 , 0.5 and 1.29 , we can get 0.04550.6688 , 0.12605.7. 0.6688 23.2996 XW From Theorem 1 we know that K can be chosen as 12844.2193.5 .KWX Figure 2 shows the trajectory of the external distur- bance. Figures 3 and 4 show, respectively, the position and velocity responses of nodes 14. Figure 1. The communication topology of nodes 1-4. 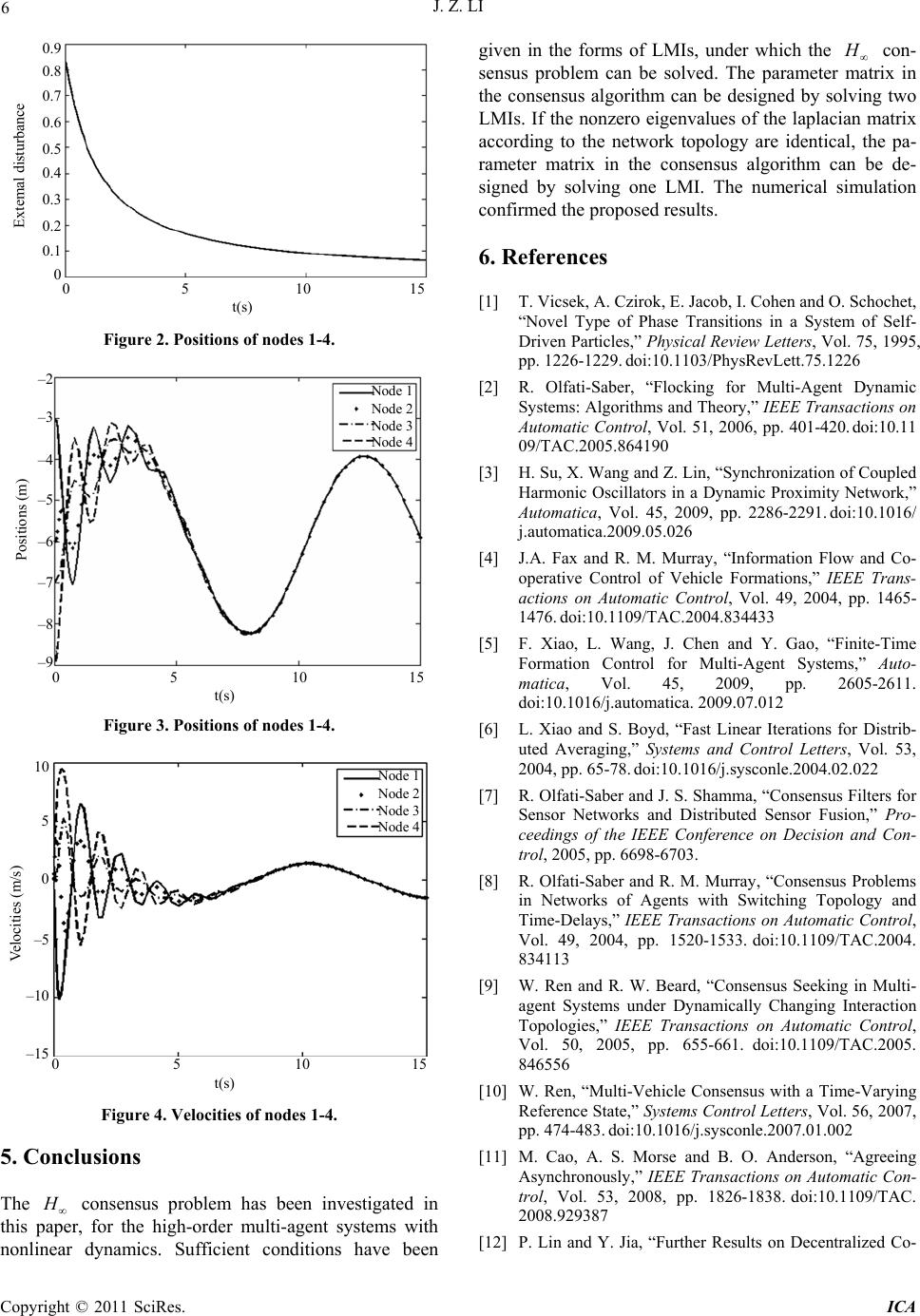 J. Z. LI Copyright © 2011 SciRes. ICA 6 0.9 0 5 10 15 t(s) Extemal dis t ur bance 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 Figure 2. Positions of nodes 1-4. – 2 0 5 10 15 t ( s ) Positions (m) – 3 – 4 – 5 – 6 – 7 – 8 – 9 N ode 1 N ode 2 N ode 3 N ode 4 Figure 3. Positions of nodes 1-4. 10 0 5 10 15 t(s) Velocities (m/s) N ode 1 N ode 2 N ode 3 N ode 4 – 15 – 10 – 5 5 0 Figure 4. Velocities of nodes 1-4. 5. Conclusions The H consensus problem has been investigated in this paper, for the high-order multi-agent systems with nonlinear dynamics. Sufficient conditions have been given in the forms of LMIs, under which the H con- sensus problem can be solved. The parameter matrix in the consensus algorithm can be designed by solving two LMIs. If the nonzero eigenvalues of the laplacian matrix according to the network topology are identical, the pa- rameter matrix in the consensus algorithm can be de- signed by solving one LMI. The numerical simulation confirmed the propose d res ults. 6. References [1] T. Vicsek, A. Czirok, E. Jacob, I. Cohen and O. Schochet, “Novel Type of Phase Transitions in a System of Self- Driven Particles,” Physical Review Letters, Vol. 75, 1995, pp. 1226-1229. doi:10.1103/PhysRevLett.75.1226 [2] R. Olfati-Saber, “Flocking for Multi-Agent Dynamic Systems: Algorithms and Theory,” IEEE Transactions on Automatic Control, Vol. 51, 2006, pp. 401-420. doi:10.11 09/TAC.2005.864190 [3] H. Su, X. Wang and Z. Lin, “Synchronization of Coupled Harmonic Oscillators in a Dynamic Proximity Network,” Automatica, Vol. 45, 2009, pp. 2286-2291. doi:10.1016/ j.automatica.2009.05.026 [4] J.A. Fax and R. M. Murray, “Information Flow and Co- operative Control of Vehicle Formations,” IEEE Trans- actions on Automatic Control, Vol. 49, 2004, pp. 1465- 1476. doi:10.1109/TAC.2004.834433 [5] F. Xiao, L. Wang, J. Chen and Y. Gao, “Finite-Time Formation Control for Multi-Agent Systems,” Auto- matica, Vol. 45, 2009, pp. 2605-2611. doi:10.1016/j.automatica. 2009.07.012 [6] L. Xiao and S. Boyd, “Fast Linear Iterations for Distrib- uted Averaging,” Systems and Control Letters, Vol. 53, 2004, pp. 65-78. doi:10.1016/j.sysconle.2004.02.022 [7] R. Olfati-Saber and J. S. Shamma, “Consensus Filters for Sensor Networks and Distributed Sensor Fusion,” Pro- ceedings of the IEEE Conference on Decision and Con- trol, 2005, pp. 6698-6703. [8] R. Olfati-Saber and R. M. Murray, “Consensus Problems in Networks of Agents with Switching Topology and Time-Delays,” IEEE Transactions on Automatic Control, Vol. 49, 2004, pp. 1520-1533. doi:10.1109/TAC.2004. 834113 [9] W. Ren and R. W. Beard, “Consensus Seeking in Multi- agent Systems under Dynamically Changing Interaction Topologies,” IEEE Transactions on Automatic Control, Vol. 50, 2005, pp. 655-661. doi:10.1109/TAC.2005. 846556 [10] W. Ren, “Multi-Vehicle Consensus with a Time-Varying Reference State,” Systems Control Letters, Vol. 56, 2007, pp. 474-483. doi:10.1016/j.sysconle.2007.01.002 [11] M. Cao, A. S. Morse and B. O. Anderson, “Agreeing Asynchronously,” IEEE Transactions on Automatic Con- trol, Vol. 53, 2008, pp. 1826-1838. doi:10.1109/TAC. 2008.929387 [12] P. Lin and Y. Jia, “Further Results on Decentralized Co-  J. Z. LI Copyright © 2011 SciRes. ICA 7 ordination in Networks of Agents with Second-Order Dynamics,” IET Control Theory and Applications, Vol. 3, 2009, pp. 957-970. doi:10.1049/iet-cta.2008.0263 [13] W. Yu, G. Chen and M. Cao, “Some Necessary and Suf- ficient Conditions for Second-Order Consensus in Multi- agent Dynamical Systems,” Automatica, Vol. 46, 2010, pp. 1089-1095. doi:10.1016/j.automatica.2010.03.006 [14] W. Yu, G. Chen, M. Cao and J. Kurths, “Second-Order Consensus for Multi-Agent Systems with Directed To- pologies and Nonlinear Dynamics,” IEEE Transactions on Systems, Man, and Cybernetics-Part B, Vol. 40, 2010, pp. 881-891. doi:10.1109/TSMCB.2009.2031624 [15] Q. Song, J. Cao and W. Yu, “Second-Order Lead- er-Following Consensus of Nonlinear Multi-Agent Sys- tems via Pinning Control,” Systems and Control Letters, Vol. 59, 2010, pp. 553-562. doi:10.1016/j.sysconle.2010. 06.016 [16] Z. Li, Z. Duan, G. Chen and L. Huang, “Consensus of Multi-Agent Systems and Synchronization of Complex Networks: a Unified Viewpoint,” IEEE Transactions on Circuits and Systems-I, Vol. 57, 2010, pp. 213-224. doi:10.1109/TCSI.2009.2023937 [17] J. H. Seo, H. Shim and J. Back, “Consensus of High- Order Linear Systems using Dynamic Out-Put Feedback Compensator: Low Gain Approach,” Automatica, Vol. 45, 2009, pp. 2659-2664. doi:10.1016/j.automatica.2009.07. 022 [18] P. Lin, Y. Jia and L. Li, “Distributed Robust H Con- sensus Control in Directed Networks of Agents with Time-Delay,” Systems and Control Letters, Vol. 57, 2008, pp. 643-653. doi:10.1016/j.sysconle.2008.01.002 [19] Z. Li, Z. Duan and L. Huang, “H Control of Net- worked Multi-Agent Systems,” Journal of Systems Sci- ence and Complexity, Vol. 22, 2009, pp. 35-48. doi:10.1007/s11424-009-9145-y [20] Y. Liu and Y. Jia, “Consensus Problems of High-Order Multi-Agent Systems with External Disturbances: An H Analysis Approach,” International Journal of Ro- bust and Nonlinear Control, Vol. 20, 2009, pp. 1579- 1593. doi:10.1002/rnc.1531 [21] Y. Liu and Y. Jia, “ H Consensus Control of Multi- Agent Systems with Switching Topology: a Dynamic Output Feedback Protocol,” International Journal of Control, Vol. 83, 2010, pp. 527-537. doi:10.1080/0020 7170903267039 [22] G. Young, L. Scardovi and N. Leonard, 2010. “Robust- ness of Noisy Consensus Dynamics with Directed Com- munication,” Proceedings of the American Control Con- ference, 2010, pp. 6312-6317. [23] S. Boyd, L. E. Ghaoui, E. Feron and V. Balakrishnan, “Linear Matrix Inequalities in Systems and Control The- ory,” SIAM Studies in Applied Mathematics. Philadel- phia, 1994. |

