J. Biomedical Science and Engineering, 2013, 6, 1155-1160 JBiSE
http://dx.doi.org/10.4236/jbise.2013.612144 Published Online December 2013 (http://www.scirp.org/journal/jbise/)
A new approach for HIV-1 protease cleavage site
prediction combined with feature selection
Yao Yuan1, Hui Liu2*, Guangtao Qiu2
1The Second Department, PLA Communication and Command Academy, Wuhan, China
2Department of Biomedical Engineering, Faculty of Electronic Information and Electrical Engineering, Dalian University of Tech-
nology, Dalian, China
Received 17 October 2013; revised 25 November 2013; accepted 5 December 2013
Copyright © 2013 Yao Yuan et al. This is an open access article distributed under the Creative Commons Attribution License, which
permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of
the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property
Yao Yuan et al. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
ABSTRACT
Acquired immunodeficiency syndrome (AIDS) is a
fatal disease which highly threatens the health of hu-
man being. Human immunodeficiency virus (HIV) is
the pathogeny for this disease. Investigating HIV-1
protease cleavage sites can help researchers find or
develop protease inhibitors which can restrain the
replication of HIV-1, thus resisting AIDS. Feature
selection is a new approach for solving the HIV-1
protease cleavage site prediction task and it’s a key
point in our research. Comparing with the previous
work, there are several advantages in our work. First,
a filter method is used to eliminate the redundant
features. Second, besides traditional orthogonal en-
coding (OE), two kinds of newly proposed features
extracted by conducting principal component analysis
(PCA) and non-linear Fisher transformation (NLF)
on AAind ex database a re used. The two new features
are proven to perform better than OE. Third, the data
set used here is largely expanded to 1922 samples.
Also to improve prediction performance, we conduct
parameter optimization for SVM, thus the classifier
can obtain better prediction capability. We also fuse
the three kinds of features to make sure comprehen-
sive feature representation and improve prediction
performance. To effectively evaluate the prediction
performance of our method, five parameters, which
are much more than previous work, are used to con-
duct complete comparison. The experimental results
of our method show that our method gain better per-
formance than the state of art method. This means
that the feature selection combined with feature fu-
sion and classifier parameter optimization can effec-
tively improve HIV-1 cleavage site prediction. More-
over, our work can provide useful help for HIV-1
protease inhibitor developing in the future.
Keywords: Dimensionality Reduction; Machine
Learning; HIV-1 Protease; Feature Fusion
1. INTRODUCTION
Acquired immune deficiency syndrome (AIDS) is quite a
mortality disease, which is due to the patients’ infection
of HIV-1. HIV-1 protease is a key enzyme in the virus
replication process, and it cleaves specific kinds of small
proteins to smaller peptides which will generate the in-
dispensable proteins for the replication process [1].
HIV-1 protease inhibitors can combine with the protease
firmly but cannot be cleaved, so the protease will not
combine with the substrates and its function will be in-
hibited. Nevertheless, it’s not practical to find inhibitors
in laboratory by conducting biological experiment, be-
cause there are too many kinds of peptides to test one by
one. Take octapeptide for example: there are 20 kinds of
amino acid residues in nature, thus there are 208 kinds of
octapeptides altogether. It’s impossible to test so many
octapeptides by biological experiment. Nevertheless,
machine learning can be used here to solve the problem
[2].
For a machine learning task, feature extraction, di-
mensionality reduction, classifier designing and perfor-
mance evaluation are of great importance, which will be
discussed as follows: octapeptide that contains eight
amino acid residues is the research object in the re-
search. In previous investigations, researchers proposed
different feature extraction methods for octapeptide se-
quence which can be mainly divided into two categories:
*Corresponding author.

Y. Yuan et al. / J. Biomedical Science and Engineering 6 (2013) 1155-1160 1156
feature extraction based on peptide sequence and phys-
icochemical properties [3]. Orthogonal encoding (OE) is
a classical feature extraction method based on sequence.
Features based on physicochemical properties can be
extracted from the Amino Acid Index Database (AAin-
dex database) which is a collection of amino acid indices
in published papers [4]. The inherently contained char-
acteristics of amino acids can provide useful information
for the prediction task [5]. Many published bioinformat-
ics investigations use data from this database [6-8]. Loris
Nanni and his colleague propose two kinds of new phys-
icochemical features using principal component analysis
(PCA) and non-linear Fisher transformation (NLF) based
on this database [9]. The two kinds of new features are
compared with OE, and turn out to perform better than
OE. For some pattern recognition tasks, if a stand alone
method is not good enough, ensembles of features can be
conducted to improve classification performance [10].
Thus the three kinds of features are fused in our research
to guarantee comprehensive representation. Feature se-
lection is mentioned that can improve classification per-
formance in their work too, and it’s a key point in this
paper.
Feature selection is an effective dimensionality reduc-
tion method, which is quite different from feature trans-
formation. It does not change the original features, but
keeps the original structure features and help under-
standing the physical meaning of data [11]. It also re-
moves redundant features and raises classifier efficiency,
thus improving prediction performance [12]. Local pre-
serving projection (LPP) is an effective feature transfor-
mation method, which retains the meaningful informa-
tion and eliminates the redundant information [13]. How-
ever, the retained information is saved in the transformed
features, difficult to understand. We expect to find the
relationship between the retained information and trans-
formed features. Thus a feature selection approach called
BPFS that approximates LPP is used to find the optimal
feature subset [14]. The subset includes features from
original features space and contains the meaningful in-
formation. BPFS has one severe drawback: the optimal
feature number of subset is not clearly defined, and dif-
ferent data might obtain their own optimal feature num-
ber of subset. In this paper, we conduct complete tests
for all subsets with different feature numbers, and calcu-
late multiple evaluation parameters to compare their pre-
diction performance, based on which to determine the
optimal feature number for each kind of original fea-
tures.
Performance evaluation is much important for a ma-
chine learning task, and different evaluation parameters
can be used. Loris Nanni and his colleague use euc
(1-auc) to evaluate their method, which is equivalent
with auc [9,15]. Auc can overall measure the perform-
ance of a classifier based on setting different classifica-
tion thresholds and calculating corresponding sensitivi-
ties and specificities. However, for our HIV-1 protease
cleavage site prediction task, the best threshold needs to
be determined in order to provide best prediction capa-
bility. Matthew’s correlation coefficient (mcc) can per-
fectly evaluate the prediction performance of our work
using the best classification threshold [16]. It takes sensi-
tivity and specificity into consideration at the same time.
Also we calculate accuracy, sensitivity, specificity, and
auc to better evaluate our work; all of them have their
own characteristics and advantages. Especially mcc is
the most important evaluation parameter.
The rest of this paper is organized as follows: Section
2 introduces the data set and the feature selection method.
Section 3 shows the results of experiments and presents
the detailed analysis of the results. At last Section 4 pro-
vides the conclusion.
2. METHODS
2.1. Data Set
There are 208 kinds of octapeptides, which is a very big
number. To effectively investigate inhibitor prediction,
date set should contain as many samples as possible to
make sure the completeness of data set. The bigger data
set, the more helpful is the prediction result. In previous
papers some classic data sets have been collected and
analyzed. The most famous one is the 362 data set which
is collected by Cai and Chou [17]. Another relatively
bigger one is the 746 data set, which is collected by You,
Garwicz and Rognvaldsson [18]. To enlarge the data set,
392 new octapeptides are added to the 362 data set by
Hyeoncheol Kim, Tae-Sun Yoon and their colleagues,
thus generating a 754-sample data set [19]. The largest
data set mentioned in the published investigations is the
1625 data set which is collected by Kontijevskis and his
colleagues [20]. To get a larger data set, we fuse all the
data sets above and get 3618 samples. After removing
contradictory and redundant samples, there are 1922 oc-
tapeptides including 596 positive samples and 1326
negative samples. This dataset is called 1922 data set.
2.2. Feature Selection
A filter method named BPFS is used here to eliminate
the redundant features. BPFS is newly proposed to con-
duct feature selection, which transforms the original
high-dimensionality features into a lower dimensionality
space by a binary projection matrix (all the elements in it
are 0 or 1), thus accomplishing feature selection. Corren-
tropy is used as the evaluation function. The approach of
BPFS is to make sure the correntropy between the subset
and the labels of samples is a maximum. Assume there

Y. Yuan et al. / J. Biomedical Science and Engineering 6 (2013) 1155-1160 1157
are two data sets


1,,
N
X
xx and


1,,
N
Yy y
which contain N samples. Then the correntropy of X and
Y can be calculated according to Eq.1.



22
1
1
;exp
N
ii
i
VXYx y
N



 (1)
At the beginning of this algorithm, LPP is carried out
to get the mapping matrix C. Assume the data set con-
tains n samples. The original feature number of data is d,
and the feature number after conducting LPP is p. The
feature selection model is like this: a data set dn
X
R


contains n samples and each sample is represented by a
d-element vector xi; learn a mapping matrix
which maximizes the objective func-
tion J(W). Here W is a 0-1 matrix. Assume that the n
samples in data set belong to Nc different classes and the
sample number of the class xi belongs to is ni.

pd
WR pd



Let Y is the data set after feature selection, then Y =
WX. J(W) can be represented by the correntropy between
Y and C, as shown in Eq.2.
 

arg max,;
,2
W
iii
i
WJWJWVW
ng WxC




XC
1
1
(2)
Here .

,0,Wij
For all i and j, , and
 
11
,1, ,
dp
ji
Wij Wij





22
,expgx yx y

  .
A series of math operations prove that the task to find
the best projection matrix can be converted to a binary
programming problem, and we use Hungary algorithm to
solve this binary programming problem. A drawback of
BPFS is that the inherent dimension of data is not deter-
mined, thus the optimal feature number of subset is not
affirmed. In the following part, we will determine the
best feature number of subsets for each kind of features.
2.3. Optimization for Subset Feature Number
BPFS is an effective feature selection method while the
feature number of subset need to be set before using it.
Thus before conducting BPFS on the three kinds of fea-
tures, the optional p values for them should be affirmed.
Here p is determined by completely testing all subsets
with different p values. Take OE for example, each
amino acid residue is represented by a 20-bit vector.
Thus an octapeptide sequence is represented by a 160-
feature vector, which means the feature number of the
original OE data is 160. In the beginning p is set to 1 and
BPFS is conducted, then a subset containing one feature
is got. Carry out 10-fold cross validation on this subset,
compute four evaluation parameters (accuracy, sensitiv-
ity, specificity and mcc) and save them. Then p is set to 2
and same work is done as mentioned previously. Each
time make sure p is added by 1 and do the work. Repeat
this process until p is 160. When all the work is done the
evaluation parameters for each value of p is saved, ac-
cording to which the optimal p is determined.
The principle we follow is to make sure the parameter
obtains a relatively high value, and starting from this
point all the values following are relatively high. Com-
prehensively consider the values of all the parameters for
all different subsets and finally determine the optimal p
value. For example the original feature number of OE for
an octapeptide is 160. Figure 1 shows all the parameter
values of different subsets. The abscissa of each sub-
graph denotes the feature number of each subset, and the
ordinate of each subgraph denotes the value of each
evaluation parameter for different subsets. When the
subset includes 120 features, the four parameters get
relatively high values and the following values are high
too. Thus p is set to 120 for OE. For PCA based features,
each amino acid residue is represented by a 19-element
feature vector, thus an octapeptide sequence can be rep-
resented by a 152-feature vector. And for NLF based
features, each amino acid residue is represented by an
18-element feature vector, thus an octapeptide sequence
can be represented by a 144-feature vector. Repeat the
same work for PCA and NLF based features, and the
optimal p values for them are 124 and 106. In the fol-
lowing part, the prediction capability of the three optimal
subsets is examined.
3. EXPERIMENTS AND DISCUSSIONS
In order to comprehensively analyze and compare the
experiment results, multiple evaluation parameters are
used in this paper: accuracy, sensitivity, specificity, mcc
and auc. Different from Loris Nanni’s work, in which
only euc is used, our work can effectively assess the ex-
periment results and provide instruction for HIV-1 pro-
tease inhibitors designing.
In order to get excellent prediction capability, pa-
rameter optimization is conducted for SVM in this paper.
The radial basis function (RBF) is chosen as the kernel
function in this work. Here accuracy, mcc and auc are
separately used to determine the optimal C and g values
by 10-fold cross validation. The three parameters are
unbiased thus can evaluate the classification performance
effectively. The range of C is set between 20 and 25, and
the range of g is set between 2−5 and 20. Each time the
index of base 2 increases by 0.5 until it reaches the ceil-
ing value. The results of parameter optimization are
shown in Table 1. The optimal C and g are determined
according accuracy, mcc and auc respectively.
First we use accuracy to determine the optimal C and
g. Then test the prediction performance by 10-fold cross
validation and calculate the five evaluation parameters.
Table 2 shows the detailed results of each kind of fea-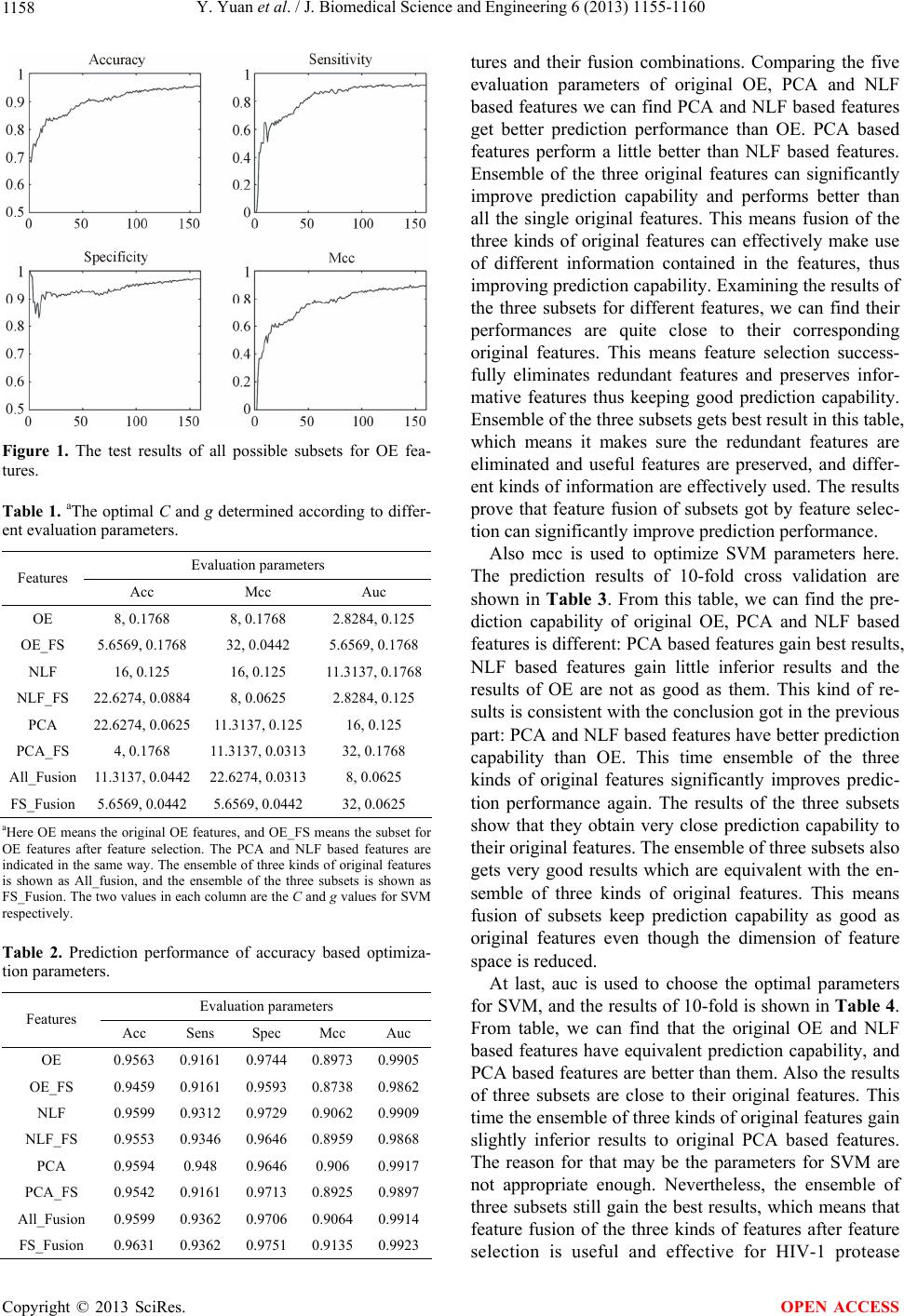

Y. Yuan et al. / J. Biomedical Science and Engineering 6 (2013) 1155-1160 1158
Figure 1. The test results of all possible subsets for OE fea-
tures.
Table 1. aThe optimal C and g determined according to differ-
ent evaluation parameters.
Evaluation parameters
Features
Acc Mcc Auc
OE 8, 0.1768 8, 0.1768 2.8284, 0.125
OE_FS 5.6569, 0.1768 32, 0.0442 5.6569, 0.1768
NLF 16, 0.125 16, 0.125 11.3137, 0.1768
NLF_FS 22.6274, 0.0884 8, 0.0625 2.8284, 0.125
PCA 22.6274, 0.0625 11.3137, 0.125 16, 0.125
PCA_FS 4, 0.1768 11.3137, 0.0313 32, 0.1768
All_Fusion 11.3137, 0.0442 22.6274, 0.0313 8, 0.0625
FS_Fusion 5.6569, 0.0442 5.6569, 0.0442 32, 0.0625
aHere OE means the original OE features, and OE_FS means the subset for
OE features after feature selection. The PCA and NLF based features are
indicated in the same way. The ensemble of three kinds of original features
is shown as All_fusion, and the ensemble of the three subsets is shown as
FS_Fusion. The two values in each column are the C and g values for SVM
respectively.
Table 2. Prediction performance of accuracy based optimiza-
tion parameters.
Evaluation parameters
Features
Acc Sens Spec Mcc Auc
OE 0.9563 0.9161 0.9744 0.8973 0.9905
OE_FS 0.9459 0.9161 0.9593 0.8738 0.9862
NLF 0.9599 0.9312 0.9729 0.9062 0.9909
NLF_FS 0.9553 0.9346 0.9646 0.8959 0.9868
PCA 0.9594 0.948 0.9646 0.906 0.9917
PCA_FS 0.9542 0.9161 0.9713 0.8925 0.9897
All_Fusion 0.9599 0.9362 0.9706 0.9064 0.9914
FS_Fusion 0.9631 0.9362 0.9751 0.9135 0.9923
tures and their fusion combinations. Comparing the five
evaluation parameters of original OE, PCA and NLF
based features we can find PCA and NLF based features
get better prediction performance than OE. PCA based
features perform a little better than NLF based features.
Ensemble of the three original features can significantly
improve prediction capability and performs better than
all the single original features. This means fusion of the
three kinds of original features can effectively make use
of different information contained in the features, thus
improving prediction capability. Examining the results of
the three subsets for different features, we can find their
performances are quite close to their corresponding
original features. This means feature selection success-
fully eliminates redundant features and preserves infor-
mative features thus keeping good prediction capability.
Ensemble of the three subsets gets best result in this table,
which means it makes sure the redundant features are
eliminated and useful features are preserved, and differ-
ent kinds of information are effectively used. The results
prove that feature fusion of subsets got by feature selec-
tion can significantly improve prediction performance.
Also mcc is used to optimize SVM parameters here.
The prediction results of 10-fold cross validation are
shown in Table 3. From this table, we can find the pre-
diction capability of original OE, PCA and NLF based
features is different: PCA based features gain best results,
NLF based features gain little inferior results and the
results of OE are not as good as them. This kind of re-
sults is consistent with the conclusion got in the previous
part: PCA and NLF based features have better prediction
capability than OE. This time ensemble of the three
kinds of original features significantly improves predic-
tion performance again. The results of the three subsets
show that they obtain very close prediction capability to
their original features. The ensemble of three subsets also
gets very good results which are equivalent with the en-
semble of three kinds of original features. This means
fusion of subsets keep prediction capability as good as
original features even though the dimension of feature
space is reduced.
At last, auc is used to choose the optimal parameters
for SVM, and the results of 10-fold is shown in Table 4.
From table, we can find that the original OE and NLF
based features have equivalent prediction capability, and
PCA based features are better than them. Also the results
of three subsets are close to their original features. This
time the ensemble of three kinds of original features gain
slightly inferior results to original PCA based features.
The reason for that may be the parameters for SVM are
not appropriate enough. Nevertheless, the ensemble of
three subsets still gain the best results, which means that
feature fusion of the three kinds of features after feature
selection is useful and effective for HIV-1 protease

Y. Yuan et al. / J. Biomedical Science and Engineering 6 (2013) 1155-1160 1159
Table 3. Prediction performance of mcc based optimization
parameters.
Evaluation PArameters
Features
Acc Sens Spec Mcc Auc
OE 0.9568 0.9144 0.9759 0.8984 0.9911
OE_FS 0.9391 0.9195 0.948 0.8594 0.9847
NLF 0.9594 0.9262 0.9744 0.9048 0.9909
NLF_FS 0.9568 0.9463 0.9615 0.9002 0.9877
PCA 0.9594 0.9346 0.9706 0.9052 0.9922
PCA_FS 0.9553 0.9413 0.9615 0.8964 0.9883
All_Fusion 0.9599 0.9379 0.9698 0.9065 0.9919
FS_Fusion 0.9599 0.9396 0.9691 0.9066 0.9917
Table 4. Prediction performance of auc based optimization
parameters.
Evaluation parameters
Features
Acc Sens Spec Mcc Auc
OE 0.9527 0.9211 0.9668 0.8892 0.9908
OE_FS 0.9448 0.9195 0.9563 0.8718 0.9859
NLF 0.9547 0.9111 0.9744 0.8935 0.9907
NLF_FS 0.9568 0.9312 0.9683 0.8991 0.9894
PCA 0.9584 0.9346 0.9691 0.9028 0.9919
PCA_FS 0.9542 0.9111 0.9736 0.8923 0.9903
All_Fusion 0.9563 0.9144 0.9751 0.8972 0.9912
FS_Fusion 0.9594 0.9312 0.9721 0.905 0.9917
cleavage site prediction.
Comparing all the results shown in the three tables, we
can find the best results are feature fusion of the three
subsets using the SVM parameters optimized based on
classification accuracy. Its mcc and auc values are the
largest in all the experiment results. The other three
evaluation parameters also get very high values. In Loris
Nanni’s work, only one kind of evaluation parameter is
used: euc, which can be calculated by 1-auc. Our work
provides five parameters to evaluate prediction perform-
ance, because only one kind of parameter isn’t enough to
effectively measure the results. Though the best euc got
in Loris Nanni’s work is 0.007, and the best euc in our
work is 0.008 (1 − 0.992), our work gets quite high mcc
value. Euc can measure the overall performance of a
classifier testing different classification thresholds, but
the most important point of HIV-1 protease cleavage site
prediction task is to train a good classifier with optimal
parameters to accomplish a good prediction model. Find-
ing the only best threshold can affirm the classifier has
best prediction capability, and mcc can perfectly evaluate
the prediction performance using the optimal parameters
and classification threshold. The best results in our work
are pleasantly surprising. The best mcc in our work is
0.914 which is quite a high value. It is reasonable to be-
lieve that our results are better than the state of art results,
and also Loris Nanni’s results. Our work can provide
much useful help for researchers and doctors to discover
or design HIV-1 protease inhibitors in the future.
4. CONCLUSION
Feature selection is a new approach for HIV-1 protease
cleavage site prediction. Different from traditional meth-
ods, our work eliminates the redundant features, simpli-
fies the feature structure and improves prediction per-
formance. Physicochemical properties of amino acid
residues provide a lot of useful information and we try to
make good use of them for the prediction task. Thus two
newly proposed kinds of features extracted from AAin-
dex database by conducting PCA and NLF are used in
this paper. Traditional OE features are also used, while
results of the experiment show that the two kinds of new
features perform better than OE. To make effective use
of the physicochemical and sequence information con-
tained in an octapeptide, we fuse the three kinds of fea-
tures to represent an octapeptide. Parameter optimization
for SVM is also conducted to improve the prediction
capability of the classifier. To make a complete com-
parison between our method and previous work, five
evaluation parameters are calculated for each kind of
work. The results turn out to be that our method gain
better prediction performance than the state of art work.
In the future, we expect to find a new feature extraction
method to generate more informative features to repre-
sent an amino acid residue. More effective feature selec-
tion methods can be used to pick out the useful and in-
formative features to improve prediction performance.
Moreover, a more successful ensemble method of fea-
tures or classifiers can be used to solve the prediction
task. Hopefully the future investigation of HIV-1 prote-
ase cleavage site will provide more useful help for HIV-1
protease inhibitor development.
5. ACKNOWLEDGEMENTS
All the work of the authors is supported by grants from the National
Natural Science Foundation of China. The foundation number is
61003175.
REFERENCES
[1] Brik, A. and Wong, C.H. (2003) HIV-1 protease: Mecha-
nism and drug discovery. Organic & Biomolecular Chem-
istry, 1, 5-14. http://dx.doi.org/10.1039/b208248a
[2] Chou, K.C. (1996) Prediction of human immunodefi-
ciency virus protease cleavage sites in proteins. Analyti-
cal Biochemistry, 233, 1-14.
http://dx.doi.org/10.1006/abio.1996.0001
[3] Nanni, L. (2006) Comparison among feature extraction

Y. Yuan et al. / J. Biomedical Science and Engineering 6 (2013) 1155-1160 1160
methods for HIV-1 protease cleavage site prediction.
Pattern Recognition, 39, 711-713.
http://dx.doi.org/10.1016/j.patcog.2005.11.002
[4] Kawashima, S., Pokarowski, P., Pokarowska, M., Ko-
linski, A., Katayama, T. and Kanehisa, M. (2008) AAin-
dex: Amino acid index database, progress report 2008.
Nucleic Acids Research , 36, 202-205.
http://dx.doi.org/10.1093/nar/gkm998
[5] Niu, B., Lu, L., Liu, L., Gu, T.H., Feng, K.Y., Lu, W.C.
and Cai, Y.D. (2009) HIV-1 protease cleavage site pre-
diction based on amino acid property. Journal of Com-
putational Chemistry, 30, 33-39.
http://dx.doi.org/10.1002/jcc.21024
[6] Du, P. and Li, Y. (2006) Prediction of protein submito-
chondria locations by hybridizing pseudo-amino acid
composition with various physicochemical features of
segmented sequence. BMC Bioinformatics, 7, 518.
http://dx.doi.org/10.1186/1471-2105-7-518
[7] Nanni, L. and Lumini, A. (2006) MppS: An ensemble of
support vector machine based on multiple physicochemi-
cal properties of amino acids. Neurocomputing, 69, 1688-
1690. http://dx.doi.org/10.1016/j.neucom.2006.04.001
[8] Sarda, D., Chua, G.H., Li, K.B. and Krishnan, A. (2005)
pSLIP: SVM based protein subcellular localization pre-
diction using multiple physicochemical properties. BMC
Bioinformatics, 6, 152.
http://dx.doi.org/10.1186/1471-2105-6-152
[9] Nanni, L. and Lumini, A. (2011) A new encoding tech-
nique for peptide classification. Expert Systems with Ap-
plications, 38, 3185-3191.
http://dx.doi.org/10.1016/j.eswa.2010.09.005
[10] Maclin, R. and Opitz, D. (1999) Popular ensemble meth-
ods: An empirical study. Journal of Artificial Intelligence
Research, 11, 169-198.
[11] Jain, A.K., Duin, R.P.W. and Mao, J. (2000) Statistical
pattern recognition: A review. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 22, 4-37.
http://dx.doi.org/10.1109/34.824819
[12] Guyon, I. and Elisseeff, A. (2003) An introduction to
variable and feature selection. The Journal of Machine
Learning Research, 3, 1157-1182.
[13] He, X. and Niyogi, X. (2004) Locality preserving projec-
tions. Neural Information Processing Systems, 16, 153.
[14] Yan, H., Yuan, X., Yan, S. and Yang, J. (2011) Corren-
tropy based feature selection using binary projection. Pat-
tern Recognition, 44, 2834-2842.
http://dx.doi.org/10.1016/j.patcog.2011.04.014
[15] Bradley, A.P. (1997) The use of the area under the ROC
curve in the evaluation of machine learning algorithms.
Pattern Recognition, 30, 1145-1159.
http://dx.doi.org/10.1016/S0031-3203(96)00142-2
[16] Powers, D.M.W. (2011) Evaluation: From precision, re-
call and f-measure to ROC, informedness, markedness &
correlation. Journal of Machine Learning Technologies, 2,
37-63.
[17] Cai, Y.D. and Chou, K.C. (1998) Artificial neural net-
work model for predicting HIV protease cleavage sites in
protein. Advances in Engineering Software, 29, 119-128.
http://dx.doi.org/10.1016/S0965-9978(98)00046-5
[18] You, L., Garwicz, D. and Rögnvaldsson, T. (2005) Com-
prehensive bioinformatic analysis of the specificity of
human immunodeficiency virus type 1 protease. Journal
of Virology, 79, 12477-12486.
http://dx.doi.org/10.1128/JVI.79.19.12477-12486.2005
[19] Kim, H., Yoon, T.S., Zhang, Y., Dikshit, A. and Chen,
S.S. (2006) Predictability of rules in HIV-1 protease clea-
vage site analysis. Lecture Notes in Computational Sci-
ence, 3992, 830-837.
[20] Kontijevskis, A., Wikberg, J.E. and Komorowski, J.
(2007) Computational proteomics analysis of HIV-1 pro-
tease interactome. Proteins: Structure, Function, and Bio-
informatics, 68, 305-312.
http://dx.doi.org/10.1002/prot.21415